Задача Лагранжа
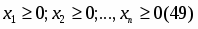
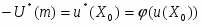

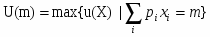
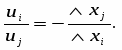
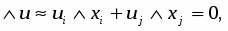
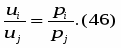
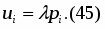
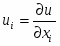
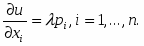
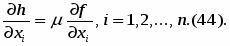
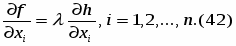
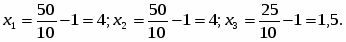
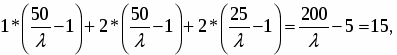
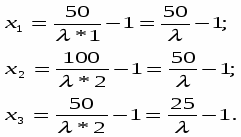
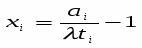
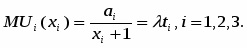
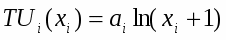
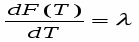
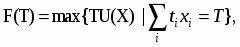
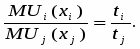
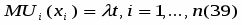
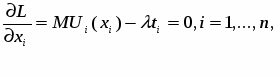
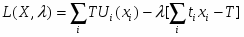
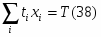
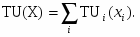
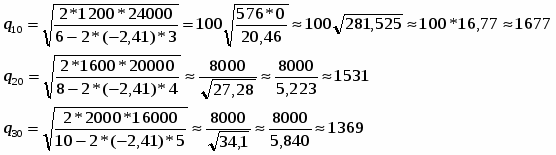
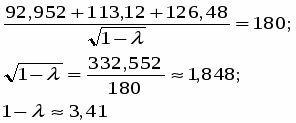
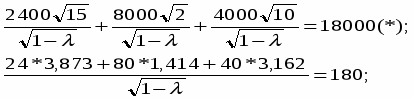
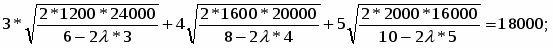
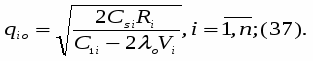
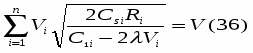
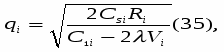
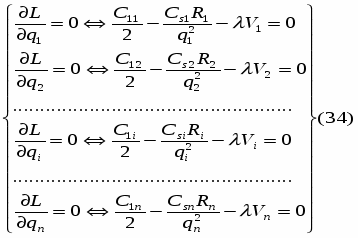
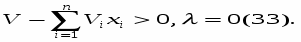
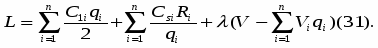
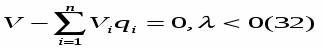
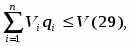
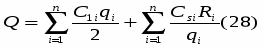
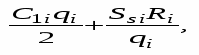
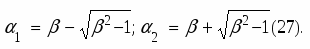
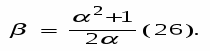
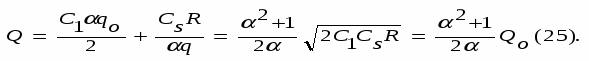
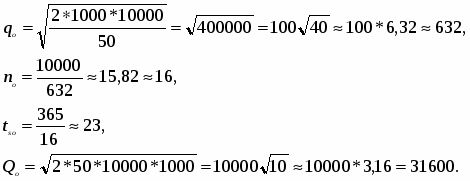
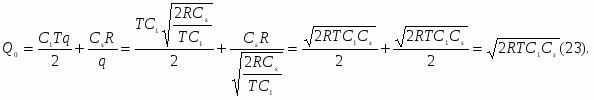
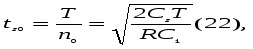
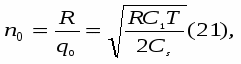
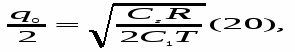
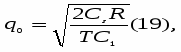
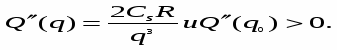
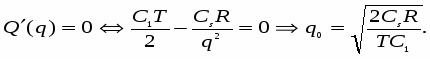
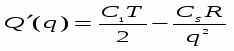
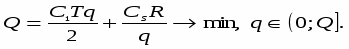
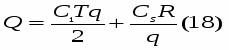
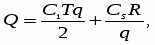
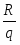
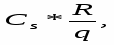
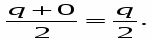
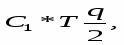
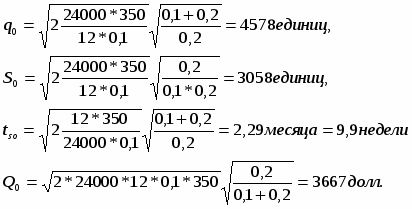
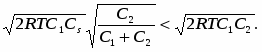
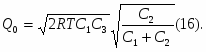
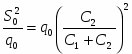
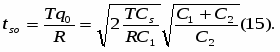
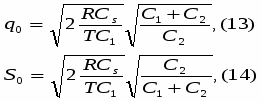
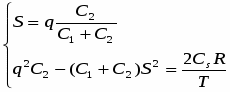
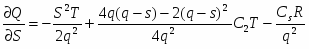
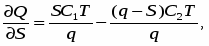
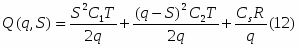
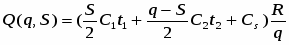
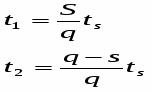
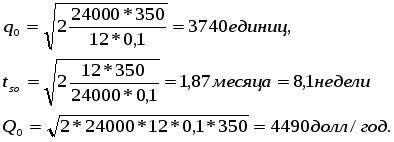
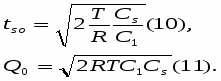
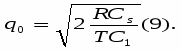
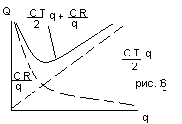
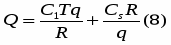
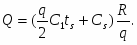
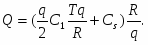
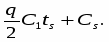
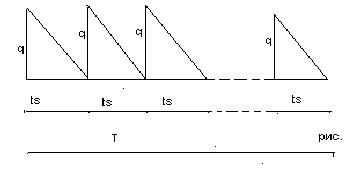
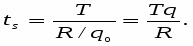
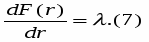
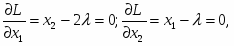
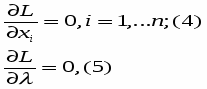
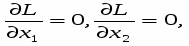

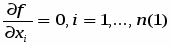 Содержание
Содержание
Введение………………………..………………………………………………2
Построение модели……………………………………………………..6
Задача Лагранжа. Безусловный и условный экстремумы……………7
Задача Лагранжа с одним ограничением……………………………..11
Смысл множителей Лагранжа………………………………………...15
Простейшая модель управления запасами…………………………...18
Модель I. Модель Уилсона без ограничений……………………..….26
Модель II. Модель Уилсона с ограничениями на складские помещения……………………………………………………………...33
Рацион Робинзона……………………………………………………...38
Взаимные экстремальные задачи……………………………………..42
Модель потребительского выбора……………………………………44
Лабораторные задачи…………………………………………………..47
Заключение……………………………………………………………..51
Список использованной литературы………………………………...………52
Введение
Научная модель является отображением некоторых интересующих нас явлений (например, определенных объектов, событий, процессов, систем) и используется в целях управления и предсказания. Основная функция научной модели заключается не в том, чтобы описать явления, а в том, чтобы объяснить их. Модель должна помочь выяснить, каким образом некоторые стороны явления влияют на другие стороны или же на явления в целом. Если построена достаточно верная модель, то эти вопросы можно выяснить, производя соответствующие опыты на модели, не меняя характеристик изучаемого объекта.
Преимущества использования модели для этих целей особенно очевидны, когда опыты на самом объекте или невозможны, как, например, в астрономии, или очень дороги, как в сложных промышленных организациях. Но знание моделей этих далеко не исчерпывается. В самом дели, в некотором смысле научные теории, объясняющие определенные явления, аналогичны моделям этого явления, потому наука не могла бы существовать без моделей, как она не могла бы существовать без теории.
Таким образом, модели играют важнейшую роль в исследовательском процессе и поэтому неизменно возрастает интерес к их изучению. Существующие модели можно разделить на три типа: изобразительные (модели геометрического подобия), модели – аналогии и символические (математические).
Изобразительная модель отображает внешние характеристики системы (как фотография и ли модель самолета). Она подобна оригиналу. Многие фотографии, картины и скульптуры являются изобразительными моделями людей, различных предметов или сцен. Игрушечный автомобиль является изобразительной моделью “настоящего” автомобиля. Глобус является изобразительной моделью земного шара. В общем случае всякое отображение представляет собой изобразительную модель в той мере, в какой его свойства совпадают со свойствами оригинала. Правда, эти свойства обычно подвергаются метрическому преобразованию, т.е. берётся определенный масштаб. Например, глобус имеет уменьшенный диаметр по сравнению с земным шаром, хотя форма и относительные размеры континентов, морей и т.д. приблизительно правильные. Модель атома, наоборот, имеет увеличенные размеры, чтобы его можно было разглядеть не вооруженным глазом. Масштаб в модели вводится для экономии и удобства пользователя. В обычных условиях гораздо легче работать с моделью здания, атома или производственной системы, чем с самим объектом. Так, с опытным заводом, который является уменьшенной моделью полного завода, работать гораздо легче, чем с настоящим заводом.
Изобразительные модели хорошо приспособлены для отображения статического или динамического явления в определенный момент времени. Например, фотография или схема производственных потоков может дать хорошую “картину” работы завода. Но такие модели не подходят для отображения динамики явлений, например для отображения рабочих операций, на заводе. Поэтому они не годятся для изучения изменяющегося процесса, или динамики системы.
Хотя изобразительная модель и подобна оригиналу, она, как и другие типы моделей, отличается от оригинала и не может отразить всех его свойств. В ней отображается только свойства оригинала, существенные для задач, решаемых с помощью данной модели. Этой избирательностью во многом определяется экономичность использования любой научной модели.
Модель – аналог использует ряд свойств одного явления для отображения свойств другого явления (например, в некоторых случаях поток воды через трубы можно принять за аналог “потока” электричества по проводам).
При построении модели различных объектов, событий, процессов или систем не всегда можно простым изменением масштаба изобразить все интересующие нас свойства. Например, мы не можем наглядно представить на глобусе геометрическую структуру Земли. Но мы легко можем представить различные геометрические формации с помощью разноцветной окраски. При этом мы производим подмену одного свойства (цвет) другим (геометрическая структура) в соответствии с некоторыми правилами преобразования. В картографии, например, такое преобразование является узаконенным, причем правила для преобразования приводятся в легенде. В легенде на карте приводится также перечень обозначений: например, сплошная линией обозначается грунтовая дорога, а пунктирной – шоссейная. Такая модель называется моделью – аналогом, поскольку в ней совокупность одних свойств представляется с помощью совокупности других свойств.
Примером простой аналогии является графики. На графиках пользуются расстоянием для отображения таких свойств, как время, число, проценты, вес, и многих других. Графики часто удобны для представления количественных соотношений и дают возможность предсказывать, как изменения одного свойства сказывается на другом свойстве.
Используя модели – аналоги, мы увеличиваем наши возможности проверять на модели изменения различных параметров. Обычно проще изменить модель – аналог, чем изобразительную модель.
Модели – аналоги удобны для отображения динамических процессов или систем. Можно построить модель, работа которой будет аналогична работе конвейера на заводе. Или можно отобразить колебания спроса путем соответствующего изменения некоторой входной величины модели. Однако на изобразительной модели, например уменьшенной действующей модели цеха, такое изменение провести трудно.
Другим преимуществом модели – аналога по сравнению с изобразительной моделью является большая универсальность этой модели. Так, незначительно изменение модели, можно отобразить различные процессы одного класса.
Символическая модель использует символы для отображения свойств изучаемой системы (с помощью математического уравнения или системы уравнений). Элементы модели и их взаимосвязь задаются с помощью символов (обычно математического или логического характера).
Во многих случаях построения моделей – аналогов затруднительно, поскольку изучение динамики явления отнимает много времени. Например, чтобы изучить с помощью аналоговой модели влияния колебания спроса на производственный процесс, нужно проделать на модели много опытов. Если же системы можно представить с помощью математического выражения, то влияние изменить какого-нибудь параметра можно установить с помощью математической дедукции за несколько шагов. Поэтому мы рассматриваем в основном символические модели.
1. Построение модели
Для постановки задачи необходима анализ системы, исследование её особенностей и возможных методов управления системой. Схема, построения в результате такого анализа, является либо изобразительной, либо аналоговой моделью. Таким образом, первый этап построения модели выполняется в процессе постановки задачи. После такого анализа системы уточняется перечень различных вариантов в решения, которые надо оценить. Затем определяются меры общей эффективности этих вариантов. Следовательно, следующий этап заключается в построении такой модели, в которой эффективность системы можно выразить в функции переменных, определяющих систему. Некоторые из этих переменных в реальной системе можно менять, другие переменные менять нельзя. Те переменные, которые можно изменить, назовем “управляемыми”. Различные варианты решения задачи необходимо выразить с помощью управляемых переменных.
Построение математической (символической) модели системы можно начать с перечисления всех элементов системы, которые влияют на эффективность работы системы. Если в качестве меры общей эффективности используется “общие ожидаемые издержки”, то можно начать с исследования изобразительной или аналоговой модели, полученной на стадии постановки задачи. Можно выделить операции и материалы, которым сопоставляется некоторые затраты. При этом получим, например, следующий исходный список:
Производственные затраты:
а) закупочная цена сырья;
б) издержки перевозки сырья;
в) стоимость приемки сырья;
г) стоимость хранения сырья;
д) стоимость планирования производства;
е) стоимость наладочных работ в цехе;
ж) стоимость процесса обработки;
з) стоимость хранения запасов в процессе производства;
и) стоимость завершения производства и передачи готовых изделий на склад;
к) стоимость анализа результатов работы группой планирования;
л) стоимость хранения готовых изделий.
Затраты на сбыт.
Накладные расходы.
2. Задача Лагранжа
Безусловный и условный экстремумы
Важное место в математиком аппарате экономики занимают оптимальные задачи – задачи, которых ищется наилучшее в определенном смысле решение. В экономической практике требуется использовать имеющиеся ресурс наиболее выгодным образом. В экономической теории одним из отправных пунктов является постулат о том, что каждый экономический субъект, имея определенную свободу выбора своего поведения, отыскивает наилучший со своей точки зрения вариант. И оптимизационные задачи служат средством описания поведения экономических субъектов, инструментом исследования закономерностей этого поведения.
Многие задачи оптимизации формулируются следующим образом. Решение, которое должен принять субъект, описывается набором чисел х1 ,х2 ,…,хn (или точкой Х=(х1 ,х2 ,…,хn) n-мерного пространства). Достоинства того или иного решения определяются значениями функция f(X) = f(х1, х2 ,…,хn) — целевой функции. Наилучшее решение — это такая точка Х, в которой функция f(Х) принимает наибольшее значение. Задача нахождения такой точки описывается следующим образом:
f(X) max.
Если функция f(X) характеризует отрицательные стороны решения (ущерб, убытки и т. п.), то ищется точка Х, в которой значение f(X) минимально:
f(X) min.
Минимум и максимум объединяются понятием экстремума. Для определенности мы будем говорить только о задачах максимизации. Поиск минимума не требует специального рассмотрения, поскольку заменой целевой функции f(X) на -f(Х) всегда можно “превратить недостатки в достоинства” и свести минимизацию к максимизации.
Из каких вариантов должен быть выбран наилучший? Иными словами, среди каких точек пространства нужно искать оптимум. Ответ на этот вопрос связан с таким элементом оптимизационной задачи, как множество допустимых решений. В некоторых задачах допустимыми являются любые комбинации чисел х1, х2,…,хn то есть множество допустимых решений - это все рассматриваемое пространство.
В других задачах следует принимать во внимание различные ограничения, означающие, что не все точки пространства доступны при выборе. В содержательных постановках задач это может быть связано, например, с ограниченностью располагаемого количества ресурсов.
Ограничения могут быть представлены в форме равенств вида
g(X) = О
или неравенства
g(X) О.
Если условия имеют несколько другую форму, скажем, g1(Х) = g2(X) или g(X) A, то их можно привести к стандартному виду, перенеся в функции и константы в одну из частей равенства или неравенства.
Экстремум, отыскиваемый во всем пространстве, без каких-либо ограничивающих условий, носит название безусловного. Если целевая функция непрерывно дифференцируема, то, необходимое условие безусловного экстремума функции состоит в равенстве нулю всех ее частных производных:
Если же заданы ограничения, то экстремум ищется лишь среди точек, которые удовлетворяют всем ограничениям задачи, так как только такие точки являются допустимыми. В этом случае экстремум носит название условного.
Рассмотрим задачу поиска условного экстремума:
f(X) max
при условиях (2)
g1(Х) = 0; g2(Х) = 0, …, gn(Х) = 0,
все ограничения которой представляют собой равенства.
Если при этом целевая функция и все ограничивающие функции непрерывно дифференцируемы, то такую задачу мы будем называть задачей Лагранжа.
3. Задача Лагранжа с одним ограничением
Рассмотрим задачу, имеющую следующую структуру:
f(X) max
при условии (3)
g(X) = 0.
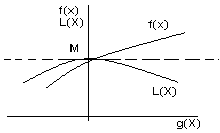
Рассмотрим пример. По склону горы идет дорога, требуется найти на ней самую высокую точку. На рис. 1 представлена карта местности с нанесенными на нее линиями
Рис. 1
равных высот; толстая линия – это дорога. Точка М, в которой дорога касается одной линий уровня, - это и есть наивысшая точка дороги.
Если Х = (х1, х2) – точка плотности, х1 и х2 – её координаты, то задаче можно придать следующую форму. Пусть f(Х) — высота точки Х над уровнем моря, а уравнение g(X) = 0 описывает дорогу. Тогда наивысшая точка дороги - решение задачи (3).
Если бы дорога проходила через вершину горы, то ее высшая точка была бы самой высокой точкой местности, и ограничение можно было бы не принимать во внимание.
Если же дорога не проходит через вершину, то, немного отклонившись от дороги, можно было бы подняться выше, чем двигаясь строго по дороге. Отклонение от дороги соответствует попаданию в такие точки, где g(X) 0; при малых отклонениях достижимую при этом высоту можно приближенно считать пропорциональной отклонению.
Идею решения задачи Лагранжа можно представить следующим образом: можно попытаться “исправить” рельеф местности так, чтобы отклонение от дороги не давало преимуществ в достижении высоты. Для этого нужно заменить высоту f(Х) функцией.
L(X) = f(X) - g(Х),
где множитель подбирается таким образом, чтобы участок склона в окрестности точки М стал горизонтальным (слишком малое не устранит преимуществ отклонений от дороги, а слишком большое – придаст преимущество отклонениям в противоположную сторону).
Теперь, поскольку рельеф L(X) делает площадку в окрестности точки оптимума горизонтальной, эта точка удовлетворяет равенствам
а так как точка лежит на дороге, то – и ограничению g(X) = 0.
рис.2
Пример с горой и дорогой — лишь иллюстрация идеи; точно так же двумерный случай использован исключительно для наглядности. Подобным образом можно было бы рассуждать и в общем, n-мерном случае.
Справедливо следующее утверждение:
Если f(х1,…,хn) и g(х1,…,хn) - непрерывно дифференцируемые функции всех своих аргументов, то решение задачи
f(х1,…,хn) max
при условии
g(х1,…,хn) = 0
удовлетворяет равенствам
где
L(х1,…,хn;) = f(х1,…,хn) — g(х1,…,хn).
Функция L(X; ) получила название функции Лагранжа (или лагранжиана) задачи (3), а коэффициент — множителя Лагранжа.
Заметим, что равенство (5) — это представленное в другой форме ограничение g(Х) = 0.
Приведенные выше рассуждения, разумеется, не являются доказательством сформулированного здесь утверждения; они лишь помогают понять существо метода: составляющая g(Х) в составе функции Лагранжа должна уравновешивать возможное увеличение максимального значения функции g(Х) от нуля. Это обстоятельство в дальнейшем будет весьма полезно при обсуждении смысла множителя Лагранжа.
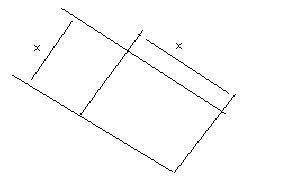
Рассмотрим чрезвычайно простой пример. Веревкой длины А требуется огородить на берегу моря прямоугольный участок наибольшей площади (берег считается прямолинейным).
Рис.3к задаче Дидона
Обозначим стороны прямоугольника х1 и х2 (см. рис. 3). Решим сначала задачу без использования метода Лагранжа.
Очевидно, х2 = А - 2 х1 и площадь прямоугольника равна S = х1х2 = x1(А - 2х1). Рассматривая ее как функцию одного аргумента х1, нетрудно найти его значение, при котором площадь максимальна: х1 = А/4. Отсюда х2 = А/2. Максимальная площадь равна S* = А2/8.
Теперь рассмотрим эту же задачу в форме задачи Лагранжа:
х1х2 max
при условии
2 х1 + х2 - А = 0
Лагранжиан этой задачи равен
L(х1,х2; ) = х1х2 - (2х1 + х2 - А),
и условия экстремума имеют вид
так что
х2 = 2
х1 =
2 х1 + х2 = А
Подставляя значения х1 и х2 из первого и второго равенств в третье, находим, что 4 = А, откуда
= А/4; х1 = А/4; х2 =А/2,
как и при решении первым способом.
Этот пример показывает распространенный способ решения задачи Лагранжа. Соотношения (4) и (5) образуют систему уравнений относительно х1,…,хn и ,. Система состоит из n + 1 уравнения - n уравнений вида (4) и одно уравнение вида (5). Число уравнений равно числу неизвестных. Из уравнений вида (4) можно попытаться выразить каждую из неизвестных х1,…,х2 через , то есть решить ее как систему из n уравнений, рассматривая как параметр. Подставляя получившиеся выражения в уравнение (5) – нам известно, что оно совпадает с ограничением, - получаем уравнение относительно . Решая его, находят , после чего определяются исходные неизвестные х1,…,хn.
4. Смысл множителей Лагранжа
При решении задачи Лагранжа мы интересовались значениями х1,…,хn; кроме того, нас могло интересовать экстремальное значение целевой функции f(X). Но в процессе решения попутно было определено значение еще одной величины - множителя Лагранжа.
Оказывается, множитель Лагранжа — весьма существенная характеристика решаемой задачи. Чтобы смысл ее стал яснее, несколько изменим формулировку ограничения, ничего не изменяя по существу.
Типичная экономическая ситуация характеризуется тем, что приходится искать наиболее выгодное решение при ограниченном количестве некоторого ресурса. Если r - заданное количество ресурса, а функция h(X) характеризует потребное его количество для достижения точки Х, то ограничению естественно придать форму
h(X) r.
По характеру задачи часто бывает ясно, что для достижения оптимума ресурс нужно использовать полностью, так что ограничение может быть записано в виде равенства
h(X) = r. (6)
Это условие можно представить в форме g(X) = h(Х) - r = 0. Но значительный интерес представляет максимально достижимый уровень функции f(x) в зависимости от имеющегося количества ресурса r. Обозначим
F(r) = max f(X) h(X) = r.
В правой части - принятое обозначение условного экстремума: после вертикальной черты выписывается условие.
Вспомним, что при обсуждении структуры лагранжиана мы интерпретировали g(Х) как составляющую, уравновешивающую возможный прирост максимума f(X) при отклонении g(X) от нуля. Но отклонение g(X) от нуля есть отклонение h(Х) от r. Если располагаемое количество ресурса получает приращение r, то мы должны ожидать приращение максимума функции f(X) на r.
В действительности это соотношение носит приближенный характер. Точный результат мы получили бы в пределе при r 0:
Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы r в ограничении вида (6).
В рассмотренном в предыдущем пункте варианте задачи Дидоны ограниченным ресурсом была длина веревки А. Максимальная площадь оказалось равной S(A) = A2/8. Отсюда dS(А)/dА = А/4, что в точности соответствует найденному при решении значению .
рис. 4
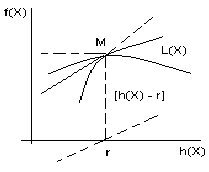
Приведем еще одно рассуждение. Для всевозможных точек Х найдем значения f(X) и h(Х) и отложим эти значения в виде точек в декартовых координатах (рис. 4). Если при каждом значении h(Х) существует максимум функции f(Х), то все точки расположатся ниже некоторой кривой, показанной на рисунке жирной линией.
Нас интересуют точки, соответствующие условию h(X) = r. Максимум f(X) помечен точкой М*; обозначим наклон кривой в этой точке. Если в качестве ординаты брать не f(X), а L(X; ) =f(X) - [h(X) — r], то новая верхняя граница имела бы в точке М* горизонтальную касательную. Это значит, что в исходном n-мерном пространстве соответствующая точка М — стационарная точка функции L (X; ) с данным значением параметра . Таким образом, - множитель Лагранжа.
Но жирная черная кривая — это график функции F(r), а - его угловой коэффициент, откуда и следует равенство (7).
5. Простейшие модели управления запасами.
Рассмотренные ниже задачи связаны с оптимальным регулированием запасов. Эти задачи можно сформулировать следующим образом:
Моменты времени, в которые принимаются заказы на пополнение запасов, фиксированы. Остается определить объем и время заказов.
Необходимо определить и объем и время заказов.
Задача исследования состоит в отыскании оптимального решения этих задач. Под оптимальным здесь понимается решение, минимизирующее сумму всех расходов, связанных с созданием запасов. Эти расходы бывают трех типов:
Расходы, вызываемые оформлением и получением заказа при закупке или производстве. Это величина, не зависящая от размера партии, и, следовательно, переменная для единицы продукции.
Стоимость хранения единицы продукции на складе. Сюда включается затраты, связанные с организацией хранения, устареванием и порчей, расходы на страхование и налог.
Расходы (штрафы), возникает при истощении запасов, когда происходит задержка в обслуживании или спрос вообще невозможно удовлетворить.
Все затраты могут оставаться постоянными или изменяться как функции времени (например, в зависимости от сезона может быть различным штраф за зависимость хранения единицы товара на складе).
В задачах управления запасами учитывается также характеристики спроса и возможности пополнения запасов.
Спрос может быть известным или неизвестным, постоянным или зависящем от времени. Величина, характеризующая спрос, может быть как дискретной (например, количество автомобилей), так и непрерывной.
Спрос на запасенные товары может возникать в определенные моменты времени (спрос на мороженое на стадионе) или существовать постоянно (спрос на мороженное в большом аэропорту).
Заказы на пополнение запасов в ряде случаев могут выполняться немедленно (например, при заказе молока в небольшом магазине). В других случаях выполнение заказа требует значительного времени. Заказы можно делать в любые или только в определенные моменты времени.
Объем поступающий на склад продукции может измеряться дискретной или непрерывной и может быть как постоянным, так и переменным. Само поступление может быть дискретным и непрерывным и происходить равномерно или неравномерно.
Примем следующие обозначения:
q - объем заказа (при пополнении запасов);
q0 - оптимальный размер заказа;
t - интервал времени;
ts - интервал времени между двумя заказами;
tso - оптимальный интервал времени между заказами;
T - период времени, для которого ищется оптимальная стратегия;
R - полный спрос за время Т;
C1 - стоимость хранения единицы продукции в единицу времени;
C2 - величина штрафа за нехватку одной единицы продукции (в определенный момент времени).
Cs - стоимость заказа ( при покупке или производстве),
Cs - ожидаемые суммарные накладные расходы;
Qo - минимум ожидаемых суммарных накладных расходов;
So - оптимальный уровень запасов к началу некоторого интервала времени.
Модель I.
Пусть некий предприниматель должен поставлять своим клиентов R изделий равномерно в течение интервала времени Т. таким образом, спрос фиксирован и известен. Нехватка товара не допускается, т.е. штраф при неудовлетворенном спросе бесконечно велик (C2 =). Переменные затраты производства складываются из следующих элементов: C1 - стоимость хранения одного изделия (в единицу времени), C2 - стоимость запуска в производство одной партии изделий.
Предприниматель должен решать, как часто ему следует организовывать выпуск партии и каким должен быть размер каждой партии.
Уравнение цен и его аналитическое решение. Только что описанная ситуация представлена графически на рис.5. Пусть q -размер партии, ts - интервал времени между запусками в производство партии, а R - полный спрос за всё времени планирования T.
Тогда R/q – число партий за время Т и
Если интервал ts начинается, когда на кладе имеется q изделий и заканчивается при.
отсутствии заказов, тогда q/2 – средний запас в течение ts (равенство q/2= qср следует рассматривать как приближенное. Точность его тем выше, чем больше R) q/2* C1 ts затраты на хранения в интервале ts.
Общая стоимость создания запасов в интервале ts равна сумме стоимости запуска в производство
Для вычисления полной стоимости создания запасов за время Т следует эту величину умножить на общее число партий за это время:
Подставляя сюда выражение для ts, получаем
или
Члены в правой части уравнений (44) представляют стоимость хранения и полную стоимость заказа в производстве всех партий. С увеличением размера партий первый член возрастает, а второй убывает. Решение задачи управления запасами и состоит в определении такого размера партии qo, при котором суммарная стоимость была бы наименьшей (рис. 6)
Найденное оптимальное значение qo размер партии
Для оптимальных tsо и Qo имеем
Пример I: Пусть предприниматель должен поставлять своему заказчику 24000 единиц продукции в год. Так как получаемая продукция используется непосредственно на сборочной линии и заказчик не имеет для нее специальных складов, поставщик должен единично отгружать дневную норму. В случаи нарушения поставок поставщик рискует потерять заказ. Поэтому нехватка продукции недопустима, т.е. штраф при нехватке можно бесконечным. Хранение единицы продукции в месяц стоит 0,1 долл. Стоимость запуска в производство одной партии продукции составляет 350 долл.
Требуется определить оптимальный размер партии q0, оптимальный период и tsо вычислить минимум общих ожидаемых годовых затрат Qо. В данном случае Т = 12 месяцам, R = 24 000 единиц, Сs = 0,1 долл./партия Сs = 350 дол/партия. Подстановка этих значений в уравнения (9), (10) и (11) дает нам.
Модель II.
Рассмотрим теперь случай, который отличается от предыдущего только тем, что превышение спроса над запасами уже допускается, т.е. штраф за нехватку конечный.
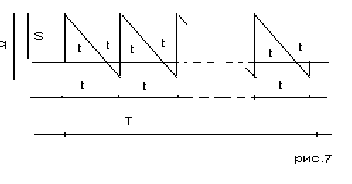
Уравнение цен и его аналитическое решение. Рассматриваемая ситуация изображена на рис. 7. В начале каждого интервала имеется уровень запасов. Из подобия треугольников находим.
Средний запас в течении t1, равен S/2. Поэтому затраты на хранение за всё время t1
составляют S/2 * t1 С1. Средняя нехватка (превышение спроса над уровнем запасов) за врем t2 равна (q-S)/2, и штраф за время t2 равна (q – S)/2, и штраф за время t2 составляет ((q – S)/2)* Q2 t2 .
Таким образом, ожидаемые суммарные расходы за всё время Т определяется следующим выражением:
Подставляя сюда найденные выше выражения для t1 и t2 учитывая полученное раннее выражение для ts, имеем
Из уравнения (12) можно найти оптимальные значения для q и S, при которых полные ожидаемый расходы будут минимальными.
После дифференцирования уравнения (12) имеем:
.
Приравнивая эти частные производные нулю и упрощая, получаем выражения,
Решая эту систему уравнений относительно S и q, находим
и, следовательно,
Что бы получить Qо, заменим, что
Поставляем (14) и (51) в (12), после упрощения получаем
При сравнении результатов, полученных для моделей I и II, можно заметить, что во первых уравнения (9), (10) и (11) можно получить из уравнения (13), (15), и (16), если в них устремиться С2 к бесконечности. Этот результат нельзя считать неожиданным, так как модель I есть частный случай модели II.
Во – вторых, если С2 , то
Следовательно, ожидаемые суммарные расходы в модели II меньше, чем в модели I.
Пример II: Пусть сохраняются все условия примера I, но только штраф С2 за нехватку теперь равен 0,2 долл. за одно изделие в месяц. И уравнения (13) – (16) получаем:
При оптимальной стратегии ожидаемый дефицит к концу каждого периода составлял бы 4578 – 3058 = 1522 изделия.
6. Модель I. Модель Уилсона без ограничений
В качестве простейшей модели управления запасами рассмотрим модель оптимизации текущих товарных запасов, позволяющих повысить эффективность работы торгового предприятия. Такая модель строится в следующей ситуации: некоторое торговое предприятие в течении фиксированного периода времени собирается завести и реализовать товар конкретного (заранее известного) объема и при этом необходимо смоделировать работу предприятия так, чтобы суммарные издержки были минимальны. При построении этой модели используется следующие исходные предложения:
планируется запасы только одного товара или одной товарной группы;
уровень запасов снижается равномерно в результате равномерно производимой продажи;
спрос и планируемом периоде заранее полностью определен;
поступление товаров производится строго в соответствии с планом, отклонения не допускаются, штраф при неудовлетворенном спросе бесконечно велик;
издержки управления запасами складывается только из издержек по завозу и хранению запасов.
Суммарные издержки будем считать зависящими от величины одной поставки q. Таким образом, задача оптимального регулирования запасов сводится к нахождению оптимального размера q0 одной постановки. Найдя оптимальное значение управляемой переменной q, можно вычислить и другие параметры модели, а именно: количество поставок n0, оптимальный интервал времени tso между двумя последовательными поставками, минимальные (теоретические) суммарные издержки Q0.
Введем следующие обозначения для заранее известных параметров модели:
T - полный период времени, для которого строится модель;
R - весь объем (полный спрос) повара за время T;
C1 - стоимость хранения одной единицы товара в единицы времени;
Cs - расходы по завозу одной партии товара.
Обозначим через Q неизвестную пока суммарную стоимость создания запасов или, что то же самое, целевую функцию. Задача моделирования состоит в построении целевой функции Q = Q(q). Суммарные издержки, будут состоять из издержек по завозу и хранению товара.
Полные издержки по хранению текущего запаса будет равны
т.е. произведению стоимости хранению одной единицы товара на “средний” текущий запас. По предложению 2 уровень запасов снижается равномерно в результате равномерно производимой продажи, т.е. если в начальный момент создания запаса он равен q, то в конце периода времени ts он стал равен 0 и тогда “средний” запас равен
Полные издержки по завозу товара будут равны
т.е. произведению стоимости завоза одной партии товара на количество поставок n, которые очевидно равны .
Тогда суммарные издержки управления текущими запасами составят
т.е. целевая функция Q является нелинейной функцией величины q, изменяющейся в пределах от 0 до R.
Таким образом, для задачи оптимального управления текущими запасами построена следующая математическая модель:
при ограничениях 0 < q Q (17)
определить значения q, обращающее в минимум нелинейную целевую функцию
Формализованная задача строго математически записывается в виде:
Решение задачи проведем по известной схеме. Вычисляем производную:
И приравниваем её к нулю:
Чтобы убедиться, что в точке q = q0 функция Q(q) действительно достигает своего минимума, вычислим вторую производную:
Итак, оптимальный размер одной поставки равен:
оптимальный средний текущий запас:
оптимальное число поставок:
оптимальный интервал между двумя последовательными поставками:
оптимальные (теоретические) издержки составят:
ПРИМЕР 1. Торговое предприятие в течение года планирует завести и реализовать сахар общим объёмом 10 тысяч тон. Стоимость завоза одной партии товара равна 1000 рублей, а хранение одной тонны сахара обходится в 50 рублей. Определить оптимальный размер одной поставки, чтобы суммарные расходы по завозу и хранению товара были минимальны, а также количество поставок, интервал времени между двумя последовательными поставками и минимальные (теоретические) суммарные издержки.
По условию задачи: R = 10000, Cs = 1000, C1 = 50, T = 12 мес.
По формулам (19), (21), (22) и (23) имеем:
Итак, оптимальный размер одной поставки равен 632 тонны, количество поставок nо равно 16, время tso между двумя последовательными поставками равно 23 дня, а минимальные суммарные расходы составят 31600 рублей.
Заметим, что условия рассмотренной задачи во многом являются идеализированными. На практике не всегда является возможным придерживаться полученных теоретических параметров модели управления запасами. Например, в рассмотренной задаче мы получили, что оптимальный размер одной поставки равен 632 тонны, но может так оказаться, что завод-изготовитель отпускает сахар только вагонами по 60 тонн. Значит, торговое предприятие вынуждено отклоняться от оптимального размера одной поставки. Поэтому важно определить такие пределы отклонения, которые не приводят к существенному возрастанию суммарных издержек.
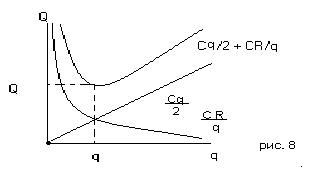
Целевая функция Q(q) управления запасами является суммой двух функций – линейной и гиперболической. Изобразим её график схематически.
В области минимума она изменяется медленно, но с удалением от точки qo, особенно в сторону малых q, величина Q быстро возрастает. Определим доступные изменения размера одной поставки по доступному уровню возрастания издержек. Пусть торговое предприятие “согласно” на возрастание минимальных издержек в не более, чем раз ( > 1), т.е. предприятие допускает издержки
Q = Qo (24)
Отклонение размера одной поставки q от оптимального зададим с помощью дополнительного параметра в виде:
q = qo.
Тогда суммарные издержки при таком размере одной поставки будет равны:
из (24) и (25) следует:
Разрешая (26) относительно получаем:
Пусть в примере 1 предприятие допускает увеличение суммарных издержек на 20% по сравнению с оптимальными, т.е. = 1,2. Тогда по формулам (27) получаем: 1 = 1,2 - 1,44 - 1 = 0,54; 2 = 1,2 + 1,44 - 1 = 1,86. И интервал допустимых величин есть 0,54 1,86. Тогда: 1qo = 0,54 * 632 341; 2qo = 1,86 * 632 1176 и объём одной постановки q может изменяться в интервале (1qo; 2q0) = (341; 1176). При этом суммарные издержки не превысят оптимальные более чем в 1, 2 раза.
Заметим здесь, что полученный допустимый интервал значений q не симметричен относительно qо, поскольку в сторону уменьшения значений q можно отклониться от qo на 632 – 341 = 291 единиц, а в сторону увеличения значений q можно отклоняться от q0 на 1176 – 632 = 544 единиц.
Такая асимметричность допустимых значений q относительно q0 легко объясняется из графика функции Q на рис.1: при отклонении влево от q0 график функции возрастает “быстрее”, чем при отклонении на такую же величину вправо от q0.
Рассмотренная выше модель конечно же достаточно проста и может применяться только на предприятиях реализующих один тип товара, что встречается крайне редко. Обычно у любого торгового предприятия имеются запасы самых различных товаров. Если при этом товар не является взаимозаменяемыми, то определение оптимальных размеров запасов производится отдельно по каждому товару, как это было показано выше. Взаимозаменяемые товары целесообразно объединить в группы и для них производить оптимизацию товарных запасов как для отдельных товаров. На практике, однако, не всегда можно воспользоваться такими рекомендациями, поскольку могут возникнуть другие ограничительные условия, в частности ограниченность размеров складских помещений. Такие ограничительные условия приводят к тому, что оптимальная по величине партия товара не может быть размещена в имеющийся складской емкости. Рассматриваемая далее модель учитывает такие ограничения.
7. Модель II. Модель Уилсона с ограничениями на складские помещения
Пусть торговое предприятие в течении периода времени Т должно завести и реализовать n видов товара. Соответственно обозначим:
Ri - полный спрос i – го товара за время Т;
C1i – стоимость хранения одной единицы i-го товара планируемом периоде времени;
CSi - расходы по завозу одной партии i – го товара;
Vi - объем складского помещения занимаемый одной единицей i –го товара.
V - вся ёмкость складского помещения.
Все эти значения считаются заранее известными. Неизвестный пока размер одной поставки i-го товара обозначим через qi, а через qio будем в дальнейшем обозначать оптимальный размер одной поставки i-го товара.
Тогда в соответствии с (2) полные издержки по завозу и хранению i-го товара будут равны:
а суммарные издержки по всем видам товара принимают вид:
Далее Vi * qi – объем складских помещений, которые занимают i-ый вид товара, Vi qi - объем складских помещений, занимаемых всеми видами товара и должно выполняться очевидные соотношения,
qi Ri, qi 0 (30).
Итак, приходим к следующей задаче Лагранжа:
Найти минимум нелинейной функции (12) при линейных ограничениях (29) и (30). Функция Лагранжа рассматриваемой задачи (28) – (30) имеет вид:
Функция Лагранжа (31) совпадает с целевой функцией (28) в случаи если в (31)
или
Следуя алгоритму решения задачи Лагранжа, найдем частные производные функции (31) по всем qi и прировняем их к нулю:
Каждое из уравнений системы (34) определяет соответствующее значение
где в правой части все значения параметров известны за исключением множителя . Для определения значения подставим выражения qi в условие (32). Получаем:
В соотношении (36) все величины, кроме , заранее известны, т.е. оно является иррациональным уравнением с одним неизвестным. Его всегда можно разрешить относительно множителя . Найдя значения = 0, можно определить оптимальные величины поставок каждого из товаров по формулам:
Теперь можно рассматривать конкретный пример.
Пусть торговое предприятие намерено завести и реализовать товар трех видов (n = 3) объемами соответственно 24 тыс. ед, 20 тыс. ед. и 16 тыс. ед. Весь объем складских помещений составляет 18 000 куб. м. Стоимость хранения одной единицы первого вида товара 6 руб., второго – 8 руб., третьего – 10 руб. Расходы по завозу одной партии первого вида товара 1200 руб., второго – 1600 руб., третьего – 2000 руб. При этом одна единица первого вида товара занимает 3 куб. м., второго – 4 куб. м., третьего – 5 куб. м. Найти оптимальные размеры поставок каждого из видов товара. По условию имеем:
R1 = 24000, R2 = 20000, R3 = 16000;
C11 = 6, C12 = 8, C13 = 10;
Cs1 = 1200, Cs2 = 1600, Cs3 = 2000;
V1 = 3, V2 = 4, V3 = 5;
V = 18000;
Составляем уравнение вида (36) для определения значения множителя ;
или
откуда о = - 2,41.
Найдем величины оптимальных поставок каждого из товаров по формулам (37):
Проверим выполнимость условия (29) при найденных объемах оптимальных поставок. Должно выполняться:
V1 * q1о + V2 * q2о + V3 * q3о V = 18000.
Имеем:
3 * 1677 + 4 * 1531 + 5 * 1369 = 5031 + 6124 + 6845 = 18000.
Выполнимость неравенства (29) служит подтверждением того, что объемы оптимальных поставок определены верно. Более того. Неравенство (29) в нашем примере выполнилось как равенство, что говорит о том, что при первом завозе товара все складские помещения будут заполнены максимально полно. С течением времени, при последующих завозах товара, картина будет конечно же не столь идеальной и какая та часть складских помещений будет не заполнена.
Здесь можем заметить одну небольшую “уловку” в этом примере исходные данные в примере подобраны так, что иррациональное уравнение (*) вида (36) имеет во всех трех слагаемых один и тот же знаменатель, что конечно же упрощает решение уравнения. Эта “уловка” использована для облегчения рассмотрения примера, поскольку нашей главной целью в настоящий момент не является возможность разрешения иррационального уравнения. И тем не менее, возникает вопрос: а что же делать, когда при использовании этой модели на практике исходные данные будут таковы, что нашей “уловкой” воспользоваться будет невозможно. Ответ на этот вопрос достаточно прост: в современной математике разработаны десятки методов приближенных решений уравнений и потому значения множителя можно определить из уравнения (36) приближенно с любой степенью точности. К тому же несмотря на нашу “уловку” облегчающую нахождения значения , тем не менее мы определили его приближение. С учетом выше сказанного, можем прийти к выводу, что использованная “уловка” не сужается общностью рассмотрения модели.
8. Рацион Робинзона
Обратимся теперь к задаче о потреблении примерно в таком виде, в каком ее ставил Госсен.
Человек может потреблять блага n видов в количествах хi, i = 1, …, n. Общая полезность потребления i-того блага описывается функцией TUi(xi). Предельная полезность MUi(хi) = dTUi(хi)/dxi убывает с ростом хi - в этом состоит закон Госсена. Полезность потребления всех: благ суммируется по отдельным благам, так что
Будем считать, опять-таки следуя Госсену, что потребительские возможности человека ограничены лишь временем, которое он может затачивать на добывание и потребление благ, как это имело место у Робинзона Крузо. Если на единицу i-того блага ему приходится тратить ti единиц времени, то ресурсное ограничение выражается равенством
где Т — фонд времени, выделяемый на потребление благ.
Задача рационального потребления теперь сводится к определению такого “рациона” - набора благ Х = (х1,…,хn), - который доставляет максимум TU(X) при ограничении (38).
Лагранжиан этой задачи:
.
Условия оптимума выражается системой
или
Итак, предельные полезности различных благ в точке оптимума пропорциональны удельным затратам времени. Это значит, что для любой пары благ (i, j) отношение их предельных полезностей равно отношению удельных затрат времени:
А отсюда следует, что дополнительная малая порция времени (скажем, минута), затрачиваемая на любое из благ, дает один и тот же прирост полезности.
Величина этого прироста, определяется коэффициентом : если Робинзон сможет выделить на потребление благ дополнительно Т единиц времени, то общая полезность возрастет при этом на величину
TU T. (40)
Заметим, что убывание предельной полезности гарантирует единственность оптимума. Если взять другие значения хi, (обозначим их хi'), также удовлетворяющие условиям, пропорциональности предельных полезностей удельным затратам времени:
MUi(xi') = i' ti
то либо ’ , тогда xi' xi. для всех продуктов (предельная полезность убывает с ростом xi); либо ’ < - для всех i. В первом случаи потребное количество времени меньше Т, во втором – больше, но ни в одном из них не ограничений будет выполнено.
Попутно отметим следующее обстоятельство. Система уравнений (40) определяет наилучший набор благ при любом фиксированном количестве Т выделенного времени; с величиной Т связано лишь численное значение . Считая величину Т переменной, введем как в предыдущем пункте, функцию.
которую можно трактовать как общую полезность времени. Это – “вторичная” полезность: её величина определяется максимальной полезностью набора благ, достижимой при данном количестве выделенного времени. Точный смысл приближенного равенства (31) состоит в том что
то есть - предельная полезность времени для Робинзона.
Как мы только что видели, сравнивая и ' для различных наборов благ, чем больше Т, тем меньше . Поскольку природа выделяемого ресурса несущественна, мы можем сделать следующий общий вывод:
если предельная полезность каждого блага снижается с ростом объема его потребления, а затраты ресурса пропорциональны объему, то предельная полезность ресурса падает с увеличением количества используемого ресурса.
Проиллюстрируем эти результаты числовым примером. Допустим, что Робинзон потребляет 3 вида благ, причем все частные функции полезности имеют один и тот же вид
с различными коэффициентами ai. Он может выделить на потребление 15 часов в сутки; остальные данные приведены в таблице:
-
t
ai
ti
1
50
1
2
100
2
3
50
2
Воспользуемся системой (30):
Отсюда
Подставим числовые значения известных параметров:
Используем теперь ресурсное ограничение:
откуда l = 200 / (15 + 5) = 10. Теперь найдем количество каждого блага:
Остальные результаты расчета приведены в таблице:
i
xi
tixi
TUi
1
4
4
80,5
2
4
8
160,9
3
1,5
3
45,8
15
287,2
9. Взаимные экстремальные задачи
Задачу Лагранжа с одним ограничением можно было бы записать в следующей форме:
f(X) – c max
при условии (41)
h(X) = r.
Вычитание константы с из целевой функции не изменяет положения оптимума. Лагранжиан этой задачи:
L(X; l) = f(X) - с - l[h(X) - r],
а условия оптимума имеют вид
Рассмотрим теперь задачу, в которой целевая и ограничивающая функции поменялись ролями:
h(X) – r min
при условии (43)
f(X) = с.
Для новой задачи лагранжиан равен
L1(Х; ) = h(Х) - r - [f(X) - с],
а условие оптимальности –
Задачи (41) и (43) называют взаимными по отношению друг к другу. Если, например, исходная задача состояла в максимизации полезности некоторого набора продуктов при заданном ресурсном ограничении, то взаимная задача состоит в минимизации расхода ресурса при обеспечении заданного уровня полезности.
Сравнение равенств (42) и (43) показывает, что условия оптимальности у обеих задач одни и те же: достаточно положить = 1/, чтобы в этом убедиться. Если l - предельная полезность ресурса, то можно было бы назвать “предельной ресурсоемкостью полезности”.
10. Модель потребительского выбора
Перейдем к рассмотрению рационального потребительского выбора в пространстве благ с теми же отношениями предпочтения. Введем в рассмотрение функцию полезности u(Х), согласованную с предпочтениями данного потребителя: u(Х) > u(у) тогда и только тогда, когда Х У. Функцию u(Х) будем считать непрерывно дифференцируемой.
При этих допущениях моделью потребительского оптимума служит задача Лагранжа
u(Х) max
при условии
рiхi = m,
где рi - цена i - го блага, а m - денежный доход потребителя. Условия оптимальности имеют вид
Введем для удобства обозначение и представим условия оптимальности в форме
Формально эта система похожа на систему (39), описывающую оптимальность в задаче о рационе Робинзона. Но здесь имеются и существенные отличия. Во-первых, теперь мы отказались от предположения о суммируемости полезностей различных благ, и ui, - не производные полезностей отдельных благ, а лишь частные производные общей функции полезности. Во-вторых, u(Х) - это не полезность в некоторой абсолютной количественной шкале, а лишь функция, согласованная с предпочтениями и отражающая только порядковые отношения. Тем не менее, перечень аналогичных свойств можно продолжить. Для любой пары благ (i, j) в точке оптимума должны выполняться соотношения
Отметим, что выражение в левой части — это норма замещения i-го блага j-м при постоянстве объемов всех остальных благ: в пределах поверхности безразличия должно выполняться равенство
то есть
Как мы уже выяснили, значение множителя Лагранжа должно выражать предельную полезность лимитирующего ресурса, в данном случае - денежного дохода (или, проще, - предельную полезность денег). Но поскольку значения функции u(Х) не являются абсолютными значениями полезности, постольку и полная полезность денег
имеет смысл лишь по отношению к выбранной шкале полезностей. То же относится и к предельной полезности денег.
Что произойдет, если функцию полезности u(Х) заменить равносильной ей функцией u*(Х)? Отношение предпочтения сохранится, если u*(Х) = (u(Х)), где (u) - монотонно возрастающая функция. Правило дифференцирования сложной функции позволяет утверждать, что
где '(u) - значение производной d (u)/du. Заметим, что множитель (u) является одним и тем же для всех благ. Поэтому условия оптимальности
ui(Х) = lpi
и
ui(Х) = l рi
определяют одно и то же положение потребительского оптимума в пространстве благ. Различаются лишь значения множителей Лагранжа:
l = j'(u) l (47)
К этому результату можно подойти с другой стороны. Задавшись некоторым значением m дохода, при использовании функций u(Х) и u*(Х) мы получим один и тот же оптимальный набор благ Х0 . Общая полезность денег в одной шкале примет значение U(m) = u(Х0), в другой . Таким образом, при любом уровне дохода
U'(m) = j(U(m)), (48)
то есть общие полезности дохода в разных шкалах связаны между собой точно так же, как и полезности наборов благ. А так как множитель Лагранжа в рассматриваемой задаче - это предельная полезность денежного дохода, то, применяя к равенству (48) правило дифференцирования сложной функции, мы снова придем к равенству (47).
Заметим, что оптимум потребителя не всегда может быть определен в рамках задачи Лагранжа. Множество допустимых решений ограничено не только бюджетом потребителя, но и условиями неотрицательности объемов благ:
Если на бюджетной поверхности норма замещения каких-либо двух благ всюду больше или всюду меньше отношения цен, то равенство (46) не может выполняться ни в одной точке. Задача не имеет внутреннего решения, а имеет угловое решение. В рамках задачи Лагранжа не могут быть описаны решения, которые лежат на границах области, определяемой неравенствами.
11. Лабораторные задачи
Задача 1: Некоторое торговое предприятие в течении промежутка времени Т собирается завести и реализовать некоторый товар R общим объёмом. Стоимость завоза одной партии равна Сs, а хранение обходится С1. Необходимо определить оптимальный размер поставки, чтобы суммарный, а так же количество поставок, интервал времени между поставками и минимальные суммарные издержки. Т.е. надо найти: qo, no, tso, Qo.
Вариант 1.
T = 24
R = 240000
Cs = 1000
C1 = 30
Вариант 2.
T = 12
R = 15000
Cs = 800
C1 = 60
Вариант 3.
T = 6
R = 9000
Cs = 450
C1 = 20
Вариант 4.
T = 12
R = 9000
Cs = 1200
C1 = 40
Вариант 5.
T = 8
R = 13000
Cs = 900
C1 = 46
Вариант 6.
T = 3
R = 5000
Cs = 300
C1 = 15
Вариант 7.
T = 12
R = 17000
Cs = 1400
C1 = 60
Вариант 8.
T = 6
R = 9000
Cs = 1300
C1 = 30
Вариант 9.
T = 24
R = 250000
Cs = 12000
C1 = 65
Вариант 10.
T = 12
R = 10000
Cs = 3000
C1 = 35
Задача 2: Торговое предприятие намерено завести и реализовать товар n видов объемами соответственно Rn. Весь объем складских помещений составляет V. Стоимость хранения одной единицы товара равна C1n. Расходы по завозу Csn. При этом каждая из n единиц занимает Vn метров. Найти оптимальные размеры поставок каждого из видов товара.
Вариант 1.
n = 2
R1 = 32000, R2 = 30000;
C11 = 9, C12 = 10;
Cs1 = 1100, Cs2 = 1350;
V1 = 2, V2 = 4;
V = 20000;
Вариант 2.
n = 4
R1 = 4000, R2 = 2000,
R3 = 5000, R4 = 5000;
C11 = 6, C12 = 7, C13 = 9,
C14= 12;
Cs1 = 1100, Cs2 = 1000,
Cs3 = 2000,
Cs4 = 3000;
V1 = 3, V2 = 5, V3 = 5, V3 = 8;
V = 24000;
Вариант 3.
n = 2
R1 = 3500, R2 = 19000;
C11 = 6, C12 = 5;
Cs1 = 1900, Cs2 = 1200;
V1 = 4, V2 = 5;
V = 25000;
Вариант 4.
n = 3
R1 = 4000, R2 = 2000,
R3 = 1000;
C11 = 8, C12 = 8, C13 = 9;
Cs1 = 200, Cs2 = 600, Cs3 = 200;
V1 = 2, V2 = 5, V3 = 3;
V = 9000;
Вариант 5.
n = 2
R1 = 4200, R2 = 2000;
C11 = 6, C12 = 8;
Cs1 = 1500, Cs2 = 1900;
V1 = 3, V2 = 6;
V = 15000;
Вариант 6.
n = 3
R1 = 24000, R2 = 19000,
R3 = 20000;
C11 = 6, C12 = 10, C13 = 10;
Cs1 = 1900, Cs2 = 2000,
Cs3 = 2000;
V1 = 7, V2 = 5, V3 = 5;
V = 30000;
Вариант 7.
n = 3
R1 = 32000, R2 = 5000,
R3 = 21000;
C11 = 8, C12 = 5, C13 = 10;
Cs1 = 1800, Cs2 = 990,
Cs3 = 1000;
V1 = 4, V2 = 2, V3 = 3;
V = 26000;
Вариант 8.
n = 2
R1 = 12500, R2 = 8200;
C11 = 3, C12 = 8;
Cs1 = 900, Cs2 = 1900;
V1 = 3, V2 = 5;
V = 15000;
Вариант 9.
n = 3
R1 = 32000, R2 = 44000,
R3 = 20000;
C11 = 8, C12 = 10, C13 = 15;
Cs1 = 1500, Cs2 = 1900,
Cs3 = 2500;
V1 = 4, V2 = 6, V3 = 8;
V = 20000;
Вариант 10.
n = 2
R1 = 26000, R2 = 17000;
C11 = 6, C12 = 3;
Cs1 = 2100, Cs2 = 1400;
V1 = 6, V2 = 4;
V = 23000.
Список использованной литературы
В.И. Варфоломеев “Моделирование элементов экономических систем”. Москва 2000г.
Бусленко Н.П. “Моделирование сложных систем” Москва, 1999г.
У. Черчмен, Р. Акоф, Л. Артоф. “Введение в исследование операций”. Наука: Москва, 1968г.
А. Будылин “Элементарные задачи”. Москва, 2002г.
Ванько В.И., Ермошина О.В., Кувыркин Г.Н. Вариацинное “Исчисление и оптимальное управление”. Москва, 1999г.
Ашманов С.А., Тимохов А.В. “Теория оптимизации в задачах и упражнениях”. Москва, 1991г.
“Лабораторный практикум по методам оптимизации”. А.Г.Коваленко, И.А.Власова, А.Ф.Федечев.- Самара, 1998г.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ