Деление двоичных чисел

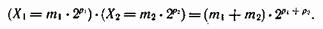


ДЕЛЕНИЕ ДВОИЧНЫХ ЧИСЕЛ
Если умножение выполняется путем многократных сдвигов и сложений, то деление, будучи операцией обратной умножению,— путем многократных сдвигов и вычитаний.
(ПРАВИЛЬНЫЕ ДРОБИ, БЕЗ ЦЕЛОГО.)
При представлении чисел с фиксированной запятой деление возможно, если делимое по модулю меньше делителя, в противном случае произойдет переполнение разрядной сетки.
Так же, как и при «ручном» делении, разряды частного при делении чисел на машине определяются (начиная со старшего) путем последовательного вычитания делителя из остатка, полученного от предыдущего вычитания. Однако здесь операция вычитания заменяется операцией сложения остатка с отрицательным делителем, представленным в обратном или дополнительном коде. Знак частного определяется сложением по модулю два кодов знаков делимого и делителя.
Рассмотрим сначала пример деления «ручным» способом.
Здесь после каждого вычитания делитель сдвигается вправо по отношению к делимому. Если остаток после вычитания получился положительный, в разряд частного записывается 1, если отрицательный — нуль. На практике обычно отрицательный остаток не записывается, просто делитель сдвигается дополнительно на один разряд вправо и вычитается из положительного остатка.
В машинах вместо сдвига делителя вправо осуществляется сдвиг остатка влево, что, по сути, ничего не изменяет.
При делении с восстановлением остатка отрицательный остаток восстанавливается суммированием с положительным делителем. Восстановленный остаток сдвигается влево на один разряд. Из сдвинутого остатка вновь вычитается делитель. По знаку полученного остатка определяется цифра очередного разряда частного. Процесс деления продолжается до получения заданного числа цифр частного, обеспечивающего необходимую точность результата.
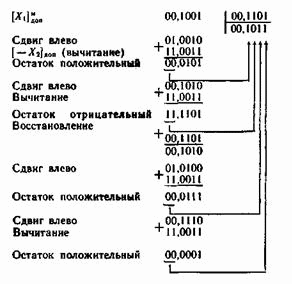
Посмотрим, как решается предыдущий пример на машине.
Процесс деления начинается со сдвига делимого влево на один разряд, после чего к нему прибавляется делитель, представленный, например, в дополнительном модифицированном коде:
Очевидно, что при делении с восстановлением остатка в самом неблагоприятном случае для формирования каждого разряда частного требуется выполнить две операции: вычитания (сложения в дополнительном или обратном коде) и сложения (восстановления остатка). То есть время выполнения операции деления может оказаться в два раза больше по сравнению с минимально возможным.
Для сокращения среднего времени выполнения операции деления реализуют деление без восстановления остатка, алгоритм которого следующий.
1) Определить знак частного суммированием по модулю два содержимых знаковых разрядов делимого и делителя.
2) Из делимого вычесть делитель. Если остаток отрицательный, перейти к пункту 3. В противном случае вычисление закончить (произошло переполнение).
3) Запомнить знак остатка.
4) Сдвинуть остаток на один разряд влево.
5) Присвоить делителю знак, обратный знаку остатка, запомненному в п. 2.
6) Сложить сдвинутый остаток и делитель (с учетом знака).
7) Присвоить цифре частного значение, противоположное коду знака остатка.
8) Повторять выполнение пунктов 3—7 до тех пор, пока не будет обеспечена требуемая точность вычисления частного.
Решение рассмотренного выше примера в данном случае осуществляется по следующей схеме:
С ПЛАВАЮЩЕЙ ЗАПЯТОЙ
При выполнении операции деления над числами с ПЛАВАЮЩЕЙ ЗАПЯТОЙ мантисса частного определяется как результат деления мантиссы делимого на мантиссу делителя, а порядок частного в результате вычитания кода порядка делителя из кода порядка делимого, так как
ДЕЛЕНИЕ ЦЕЛЫХ
Деление целых ненулевых n-разрядных (не считая знаковых разрядов) чисел А:В, представленных в прямом (для простоты) коде, приводит к получению целого частного С и целого остатка 0, которому присваивается знак делимого; знак частного вычисляется как сумма по модулю два операндов А и В.
Деление выполняется в следующей последовательности.
1) Делитель В сдвигается влево (нормализуется), так чтобы в старшем информационном разряде оказалась 1;подсчитывается количество сдвигов S; частное от деления может быть не более (S + 1) разрядов, не равных нулю.
2) Выполняется (S+1) цикл деления модулей |А| на IB’l где В' — нормализованное В, в результате находится(S+ 1) разряд частного, начиная со старшего из (S+ 1)младших.
3) Полученный в последнем цикле деления остаток Rs+1, если он положительный, сдвигается вправо на S разрядов; если же Rs+1 < 0 (отрицательный), то остаток восстанавливается: к нему добавляется |В'|, т. е.[Rs+1]вост = Rs+1+|B'|. После этого выполняется сдвиг вправо на S разрядов. В результате получается целый остаток от деления.
Частному и остатку присваиваются знаки.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ