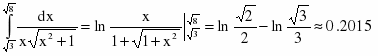
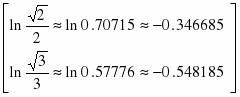
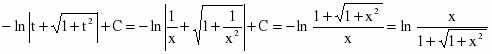
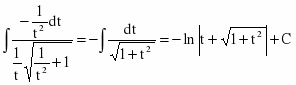
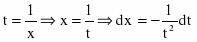
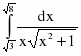
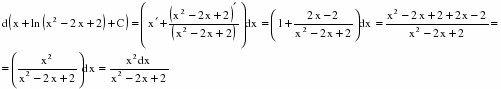
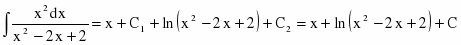
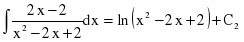
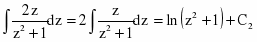
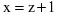
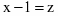
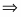
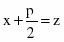
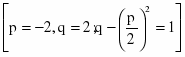
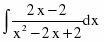
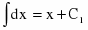
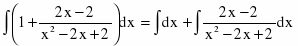
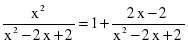
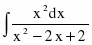
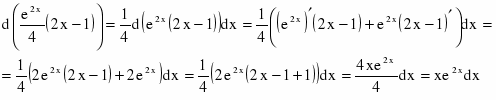
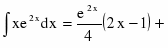
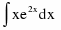
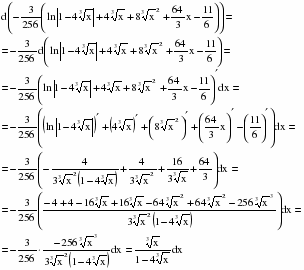
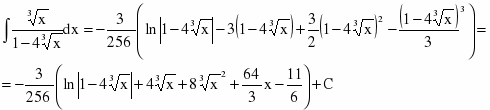
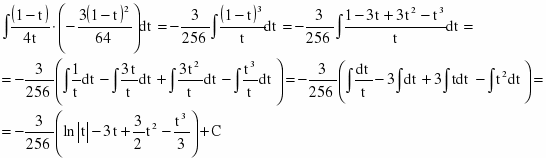
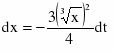
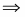
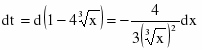
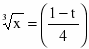
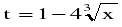
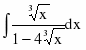
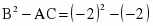
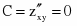
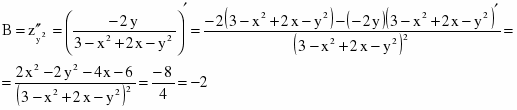
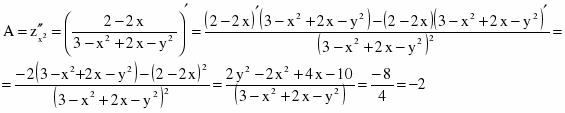
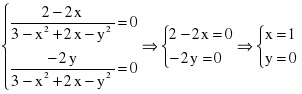
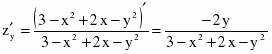
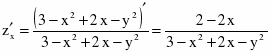
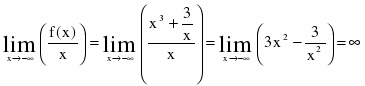
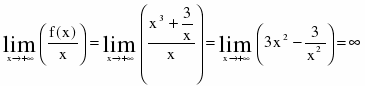
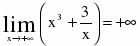
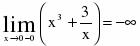
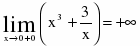
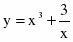
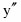
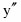
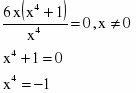
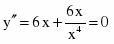
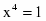
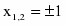
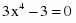
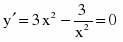
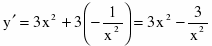
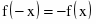
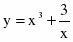
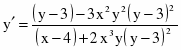
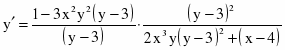
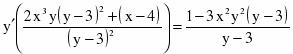
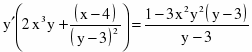
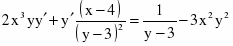
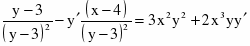
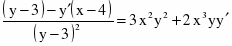
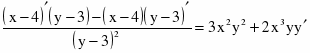
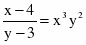
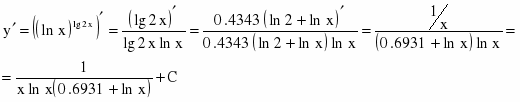
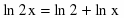
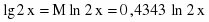
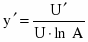
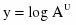
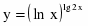
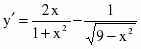
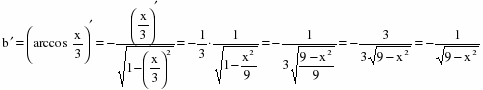
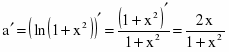
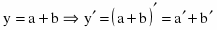
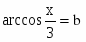
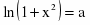
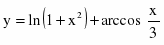Задание 1. Найти производные функций

a)

Пусть , , тогда

b)

Если функция имеет вид , то её производная находится по формуле .

Перейдем от десятичного логарифма к натуральному:

По свойству логарифма

Таким образом,

c)

Продифференцируем уравнение, считая y функцией от х:

Задание 2. Исследовать методами дифференциального исчисления и построить график функции

Областью определения функции являются все действительные числа,

кроме х=0. В точке х=0 функция разрывна.

Функция нечетная, т. к.

Функция не пересекается с осями координат (уравнение y=0 не имеет решений).

Найдем производную функции:

.

Найдем стационарные точки, приравняв производную к нулю.

+

-

+

-1

1

0

-

min

max

Функция возрастает в промежутке (-∞; – 1) U (1; ∞)

и убывает в промежутке (-1; 0) U (0; 1).

Функция имеет экстремумы: максимум – в точке х=-1, минимум – в точке х=1.

Исследуем функцию на выпуклость / вогнутость.

Для этого найдем производную второго порядка и, приравняв её к нулю, вычислим критические точки второго рода.

+

-

0

В точке х=0 вторая производная не существует, т. к. это точка разрыва функции. В интервале (-∞; 0) <0, следовательно, график функции в этом интервале выпуклый. В интервале (0;∞) >0, следовательно, график функции в этом интервале вогнутый.

Асимптоты графика функции :

1) вертикальная асимптота – прямая х=0

Т.к. и

2) горизонтальных асимптот нет,

т. к. и

3) наклонных асимптот нет,

т. к.

и

Задание 3. Найти экстремумы функции Z = ln (3 – x² + 2x – y²)

Найдем частные производные первого порядка.

М (1; 0) – стационарная точка.

Найдем вторые производные и их значения в точке М.

>0 Следовательно, функция Z = ln (3 – x² + 2x – y²) имеет экстремум в точке М (1; 0) – максимум, т. к. A< 0.

Задание 4. Вычислить неопределенные интегралы, результат проверить дифференцированием

a)

Решаем методом замены переменной. Положим ,

тогда ,

Таким образом, получаем

Вернемся к переменной х.

Проверим дифференцированием:

b)

Воспользуемся таблицей неопределенных интегралов [Выгодский, М.Я. Справочник по высшей математике. – М.: Наука, 1972. – 872 с.:ил. – С. 850]

С

Проверим дифференцированием:

c)

Неправильную рациональную дробь приводим к правильной делением числителя на знаменатель, получаем

Согласно свойству интервала алгебраической суммы, имеем

Подстановка приводит интеграл к виду

Возвращаясь к аргументу х, получаем

Таким образом, ,

где С=С₁+С₂

Проверим дифференцированием:

Задание 5. Вычислить определенный интеграл

Сначала вычислим неопределенный интеграл методом замены переменной. Полагая , находим

Вернемся к переменной х.

Таким образом,

Библиографический список

1. Баврин, И.И. Высшая математика: учебник/ И.И. Баврин. – М.: Академия, 2003. – 616 с.:ил.

2. Выгодский, М.Я. Справочник по высшей математике/М.Я. Выгодский. – М.: Наука, 1972. – 872 с.:ил.

3. Выгодский, М.Я. Справочник по элементарной математике/М.Я. Выгодский. – СПб.: Изд. «Санкт-Петербург оркестр», 1994. – 416 с.:ил.