Федеральное агентство по образованию

ГОУ ВПО "ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

Кафедра «Автоматизированные системы обработки информации и управления»

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

К КУРСОВОМУ ПРОЕКТУ

по дисциплине «Дискретная математика»

ДВУМЕРНАЯ КЛАСТЕРИЗАЦИЯ ПО ПРЕДЕЛЬНОМУ РАССТОЯНИЮ

Омск – XXX

Реферат

Отчёт 14с., 1ч., 12рис., 0табл., 3источника, 0прил.

ГРАФ, КЛАСТЕР, МИНИМАЛЬНОЕ ОСТОВНОЕ ДЕРЕВО.

Предметом курсового проекта является кластеризация.

Цель работы – разработка алгоритма кластеризации по предельному расстоянию и построение минимального остовного дерева каждого кластера.

В ходе работы был разработан алгоритм кластеризации.

В результате работы было написан алгоритм, решающий данные задачи.

Введение

Часто бывает полезно и наглядно изображать некоторую ситуацию в виде рисунка, состоящего из точек (вершин) и линий (рёбер), соединяющих некоторые вершины. Такие изображения получили названия графа.

Теория графов получила широкое применение на практике. Она применяется в гражданском строительстве, электротехнике, социологии и экономике и в других областях.

Одной из задач теории графов является кластеризация и построение минимального остовного дерева. Эти задачи часто возникают на практике: при группировке результатов поиска, проектировании компьютерных систем, соединении городов, составлении электрических цепей.

Целью данной работы является разработка алгоритма, выполняющего данные задачи.

Отчет содержит четыре раздела:

- постановка задачи курсового проектирования – это раздел, в котором описывается задача курсового проекта;

- схемы алгоритмов – это раздел, в котором описывается алгоритм и его схема;

- теоретический анализ – теория, необходимая для выполнения поставленной задачи;

- результаты тестирования – это раздел, в котором описываются результаты тестирований на правильность работы разработанного алгоритма.

1 Постановка задачи курсового проектирования

Реализовать алгоритм кластеризации заданного набора точек по предельному расстоянию d. После кластеризации граф каждого кластера редуцировать до минимального остовного дерева.

2 Теоретический анализ

Граф G - это математический объект, состоящий из множества вершин X = {x₁, x₂,..., x_n} и множества ребер A = {a₁, a₂,..., a_k}.

Связный граф — такой граф, в котором между любой парой вершин существует по крайней мере один путь.

Взвешенный граф — граф, каждому ребру которого поставлено в соответствие некоторое значение (вес ребра).

Вес ребра — значение, поставленное в соответствие данному ребру взвешенного графа. Обычно вес — вещественное число и его можно интерпретировать как «длину» ребра.

Если ребрам графа приданы направления от одной вершины к другой, то такой граф называется ориентированным. Ребра ориентированного графа называются дугами. Если направления ребер не указываются, то граф называется неориентированным (или просто графом).

Подграф исходного графа — граф, содержащий некое подмножество вершин данного графа и некое подмножество инцидентных им рёбер.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_{i j} равно числу ребёр из i-й вершины графа в j-ю вершину.

Матрица смежности простого графа является бинарной матрицей и содержит нули на главной диагонали.

Кластерный анализ — задача разбиения заданной выборки объектов (ситуаций) на подмножества, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Кластер — группа элементов, характеризуемых общим свойством.

В данном случае в кластеры объединяются точки, находящиеся на расстоянии меньше предельного d.

Лес — неориентированный граф без циклов. Компонентами связности леса являются деревья.

Дерево — это связный граф, не содержащий циклов.

Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево, имеющее минимальный возможный вес. Вес дерева — сумма весов входящих в него рёбер.

В данном курсовом проекте для построения минимального остовного дерева используется алгоритм Краскала. Рёбра графа упорядочиваются в порядке не убывания их весов и последовательно добавляются к графу. Если добавление нового ребра приведёт к образованию цикла, то это ребро пропускается. Подграф данного графа, содержащий все его вершины и найденное множество рёбер, является его остовным лесом минимального веса.

3 Схемы основных алгоритмов

3.1 Пошаговый алгоритм

Шаг 1. Заполнение матрицы весов T.

Шаг 2. Создание матрицы смежности С.

Шаг 2а. Если расстояние между двумя точками s > d, то в матрицу заносится 0, иначе 1.

Шаг 2б. Повторение шага 2 N раз;

Шаг 3. Создание матрицы минимального остовного дерева ТТ;

Шаг 3а. Если tt_ii = 0, tt_jj = 0, то tt_ij = t_ij, tt_ii = k, tt_jj = k, k = k +1, где t_ij – минимальный положительный элемент матрицы T;

Шаг 3б. Если tt_ii = 0, tt_jj ≠ 0, то tt_ij = t_ij, tt_ii = tt_jj;

Шаг 3д. Если tt_ii ≠ 0, tt_jj = 0,то tt_ij = t_ij, tt_jj = tt_ii;

Шаг 3е. Если tt_ii ≠ 0, tt_jj ≠ 0, tt_ii ≠ tt_jj ,то tt_ij = t_ij, tt_ii = l, tt_jj = l, где l – наименьшее из tt_ii и tt_jj;

Шаг 3ж. Если tt_ii ≠ 0, tt_jj ≠ 0, tt_ii = tt_jj, то t_ij = -1;

Шаг 4. Проверка диагональных элементов матрицы ТT;

Шаг 4б. Если tt_zz = 1, то повторить шаг 4. Иначе m = 0;

Шаг 5. Повторять алгоритм с шага 3 до тех пор, пока m ≠ 1;

3.2 Схема алгоритма.

Решение данной задачи состоит из нескольких этапов: кластеризации и построения минимального остовного дерева. Схемы этих алгоритмов, изображены на рисунках 2 – 4. Общая схема алгоритма изображена на рисунке 1.

Набор точек

Предельного расстояние d

Кластеризация

Построение минимального остовного дерева

Начало

ачало

Конец

ачало

Рисунок 1 – Схема основного алгоритма

Расчет матрицы T графа G

В матрицу смежности заносится 1

s_i > d

нет

да

В матрицу смежности заносится 0

i = 1,N

Начало

ачало

Конец

ачало

Рисунок 2 – Алгоритм кластеризации

Обнуление матрицы ТT

Начало

ачало

tt_ii = 0, tt_jj = 0

tt_ij = t_ij, tt_ii = k, tt_jj = k,

k = k +1

нет

да

tt_ii = 0, tt_jj ≠ 0

tt_ij = t_ij, tt_ii = tt_jj

нет

да

tt_ii ≠ 0, tt_jj = 0

tt_ij = t_ij, tt_jj = tt_ii

нет

да

tt_ii ≠ 0, tt_jj ≠ 0,

tt_ii ≠ tt_jj

tt_ij = t_ij, tt_ii = l, tt_jj = l

нет

да

m = 1

нет

tt_ii ≠ 0, tt_jj ≠ 0,

tt_ii = tt_jj

нет

да

t_ij = -1

А

В

ТT – матрица минимального остовного дерева

t_ij – минимальный положительный элемент матрицы T

l – наименьшее из tt_ii и tt_jj

Рисунок 3 – Алгоритм построения минимального остовного дерева

z = 1,N

В

А

tt_zz = 1

нет

да

m = 0

Конец

ачало

Рисунок 4 – Алгоритм построения минимального остовного дерева (продолжение)

4 Результаты тестирования

Было проведено 3 различных эксперимента.

4.1 Тест первый.

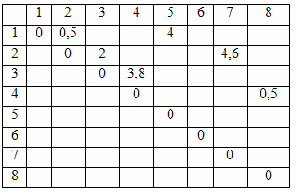
Пусть граф содержит 8 вершин, координаты которых заданы случайным образом, а взвешенная матрица Т представлена на рисунке 5. Предельное расстояние d = 5;

Рисунок 5 – Тест первый (часть 1)

Шаг 1. Обнуление матрицы дерева ТТ.

Шаг 2. Составляем матрицу смежности С.

Шаг 2а. Если расстояние между двумя точками s > d, то в матрицу заносится 0, иначе 1.

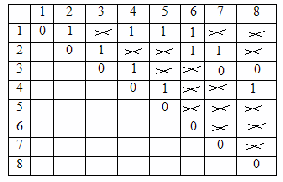
Шаг 2б. Повторение шага 2 8 раз. Полученная в результате матрица смежности представлена на рисунке 6.

Рисунок 6 – Тест первый (часть 2)

Шаг 3. Составляем матрицу дерева ТТ.

Шаг 3а. Первоначально в матрице на главной диагонали все нули, значит

tt₁₁ = tt₂₂ = ... = tt₈₈ = 0, k = 1;

Шаг 3б. Находим минимальный элемент матрицы Т - t₁₂ = 0,5. Включаем данное ребро в матрицу ТТ и увеличиваем значение счётчика k = k + 1 = 2;

Шаг 3г. Находим следующий минимальный элемент и повторяем все действия из шага 3б. Таким образом перебираем всю матрицу.

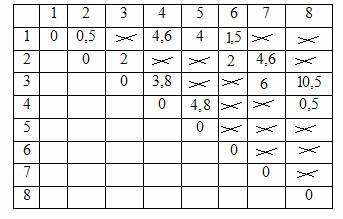
Шаг 4. На главной диагонали матрицы ТТ находятся все 1. Полученная матрица представлена на рисунке 7.

Рисунок 7 – Тест первый (часть 3)

4.1 Тест второй.

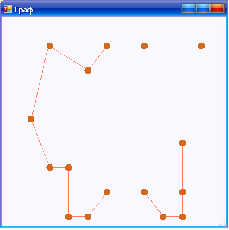
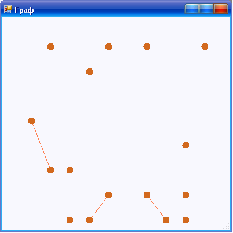
Результат выполнения алгоритма с 20-ю вершинами, заданными случайными координатами и предельным расстоянием равным 2,5 представлен на рисунке 8.

Рисунок 8 – Тест второй (часть 1)

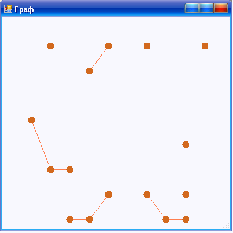
На данном рисунке видно, что граф был разбит на 8 кластеров. Увеличим предельное расстояние до 3. Из рисунка 9 видно, что количество кластеров сократилось до 4.

Рисунок 9 – Тест первый (часть 2)

Продолжая постепенно увеличивать предельное расстояние, увидим, что в итоге граф будет представлять собой один кластер. Минимальное остовное дерево этого кластера представлено на рисунке 10.

Рисунок 10 – Тест первый (часть 3)

Из этого теста видно, что с увеличением предельного расстояния количество кластеров уменьшается. Минимальное остовное дерево строится верно. Значит, в данном тесте программа работает верно.

4.3 Тест третий

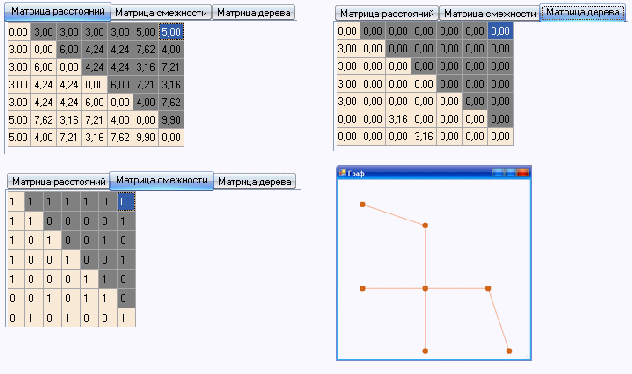
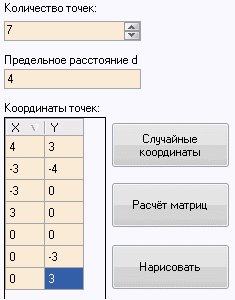
Составим граф из 7 вершин, координаты которых и предельное расстояние представлены на рисунке 11.

Рисунок 11 – Тест второй (часть 1)

Построим данный граф. Остовное дерево данного графа, а так же матрицы смежности, расстояний и остовного дерева представлены на рисунке 12.

Рисунок 12 – Тест второй (часть 2)

Заключение

При рассмотрении данной задачи был изучен один из разделов теории графов кластеризация и построение минимального остовного дерева по алгоритму Краскала.

Результатом курсового проекта является алгоритм, выполняющий необходимые задачи.

Список использованных источников

1 Канева О.Н. Дискретная математика. – Омск: ОмГТУ, 2009. -87с.

2 Кристофидес Н. Теория графов. Алгоритмический подход.- М.: Мир, 1978.-433с.

3 Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2000. -304с.