Эконометрика 8
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
ИНСТИТУТ ЭКОНОМИКИ И ВНЕШНЕЭКОНОМИЧЕСКИХСВЯЗЕЙ
Контрольная работа по предмету:
«ЭКОНОМЕТРИКА»
Студентки 1 курса
Группы 2009-2 МЭ
Кощиенко Евгении
Ростов – на – Дону
2009
Целью данной контрольной работы является построение и анализ функции спроса на товар А. Эконометрические модели спроса строятся в виде уравнений парной и множественной регрессии, в которых в качестве зависимой пе ременной величины (функции) выступает спрос, а в качестве независимых переменных величин (аргументов) - формирую щие его причинные факторы. Наиболее существенными факто рами, оказывающими влияние на спрос, являются: цена на дан ный товар, цены на другие товары, доход, половозрастной со став семьи, размер семьи, вкусы и привычки и т.д. Как прави ло, анализ спроса начинают с построения функции одной пе ременной. Для этого все факторы, кроме одного, считают неиз менными или закрепляют на каком-либо уровне. Если в каче стве формирующего фактора выбрать цену на данный товар, то получим так называемую функцию спроса от цены. Если же в качестве аргумента выбрать доход, то получим функцию по требления (функцию спроса от дохода).
Очевидно, что все это многообразие факторов не может быть непосредственно включено в эконометрическую модель спроса. В модели учитываются лишь наиболее существенные факторы, то есть те, которые вызывают значительные изменения в спросе населения на данный товар, оказывают определяющее воздействие на процесс формирования и развития этого спроса. Хотя реальный спрос находится под влиянием всех переменных, используя принцип «при прочих равных условиях», мы можем вычленить степень влияния отдельной переменной и составить уравнения для каждой детерминанты, принимая остальные постоянными.
Эффективными методами отбора наиболее существенных факторов являются качественный анализ, корреляционный анализ, а также анализ результатов специально проводимых опросов мнений специалистов (экспертных оценок).
С конца 19-го века, когда немецкий статистик Энгель сформулировал законы изменения спроса на различные товары в зависимости от изменения дохода потребителя, в качестве важнейшего фактора, влияющего на потребление товаров, рассматривается денежный душевой доход.
В зависимости от используемых математических методов различают структурные и функциональные модели спроса. Структурные модели исходят из того, что для каждой доходной группы населения по бюджетным данным может быть рассчитана свойственная ей структура потребления. Из всех факторов, под влиянием которых формируется эта структура, изменяемым считается только доход, а прочие факторы принимаются постоянными. Изменение дохода рассматривается как перемещение определенного количества семей из одних доходных групп в другие.
В структурной модели используются фактические нормы потребления, исчисленные по статистическим данным, которым присущи случайные отклонения и ошибки, поэтому при анализе и прогнозировании спроса эти нормы выравнивают при помощи построения функциональной модели спроса.
Итак, для выполнения нашей работы выберем в качестве аргумента доход и получим функцию по требления (функцию спроса от дохода).
В процессе выполнения работы необходимо выполнить три цикла эконометрического исследования, каждый из которых состоит из шести этапов:
1 этап (постановочный): определение конечной цели моделирования, набора участвующих в модели факторов и показателей на основе качественного анализа иссле дуемого экономического процесса.
2 этап (априорный): предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации.
3 этап (параметризация): моделирование, т.е. выбор общего вида математической модели процесса, состава и формы входящих в нее связей.
Основная задача, решаемая на этом этапе, - спецификация модели, т.е. выражение в математической форме обнаруженных связей и соотношений; установление состава эндогенных и экзогенных переменных; формулировка исходных предпосылок и ограничений модели. От того, насколько удачно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования.
4 этап (информационный): формирование репрезентативной выборочной статистической сово купности, сбор необходимой статистической информации: регистрация значений участвующих в модели факторов и показателей на различных временных и пространственных интервалах функционирования явления.
5 этап (идентификация модели): статистический анализ модели, прежде всего, выбор методов оценивания неизвестных параметров модели в соот ветствии с особенностями объектов исследования и спецификой имеющихся данных наблюдений и статистическое оценивание этих параметров.
6 этап (верификация модели): сопоставление модельных и расчетных данных, проверка адекватности модели, оценка точности модельных данных. На этом этапе рассчитываются:
коэффициенты корреляции (корреляционное отношение) и детерминации, используемые для проверки пра вильности произведенного отбора факторов и принятой формы связи;
эмпирические и теоретические коэффициенты эластичности зависимой переменной по факторам, сравнение которых между собой также применяется в качестве критерия проверки адекватности модели;
статистические t – критерий и F – критерий, а также их доверительные интервалы, для проверки статистической значимости коэффициентов регрессии и детерминации соответственно.
Первый цикл, включает обоснование и проверку адекватности линейной модели парной регрессии, независимым фактором в которой является денежный доход потребителя. Исходные данные для выполнения этого цикла приведены в приложении (y обозначает спрос на товар А, х – средний доход в расчете на 1 человека).
Во втором цикле для тех же исходных данных в соответствии со всеми шестью этапами анализируется степенная функция.
В третьем цикле добавляется еще один фактор – размер семьи и анализируется линейная модель множественной регрессии.
В результате проверки по всем необходимым критериям должен быть сделан выбор в пользу одной из трех исследованных моделей.
Первый цикл.
Обоснование и проверка адекватности линейной модели парной регрессии, независимым фактором в которой является денежный доход потребителя.
Исходные данные, характеризующие изменение среднего душевого дохода в расчете на 1 человека - (Х) и расхода на потребление товара А (спрос на товар А) - (Y) приведены в таблице 1.
Таблица 1 - Исходные данные
Вариант 1.16
Душевой доход
(X) (ден.ед.)
Расход на потребление
товара А (Y) (ден.ед.)
X²
XY
Y²
200
120
40 000
24 000
14 400
250
129
62 500
32 250
16 641
300
135
90 000
40 500
18 225
350
140
122 500
49 000
19 600
400
145
160 000
58 000
21 025
450
151
202 500
67 950
22 801
500
155
250 000
77 500
24 025
550
160
302 500
88 000
25 600
600
171
360 000
102 600
29 241
650
182
422 500
118 300
33 124
700
189
490 000
132 300
35 721
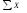 = 4950
= 4950
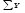 = 1677
= 1677
 = 2 502 500
= 2 502 500
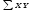 = 790400
= 790400
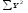 =
=
260 403
3308507 507 507130011
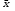 = 450
= 450
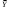 = 152,4545
= 152,4545
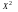 = 227 500
= 227 500
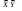 = 71854,55
= 71854,55
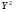 =
=
23 673
Определение формы связи между результирующим (У) и объясняющим (Х) фактором и расчёт параметров уравнения парной регрессии.
Задачу определения парной регрессии можно сформулировать следующим образом: по наблюденным значениям одной переменной (X) нужно оценить или предсказать ожидаемое значение другой переменной (Y).
В модели линейной регрессии теоретически предполагается существование между переменными X и Y связи следующего вида:
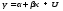 ,
,
где y - зависимая, объясняемая переменная, результирующий признак, регрессант;
х - независимая, объясняющая переменная, регрессор, факторный признак;
U – остаточная компонента, случайный член;
, β - неизвестные параметры.
Уравнение (1) называется регрессионным уравнением.
Задача регрессионного анализа состоит в получении оценок неизвестных параметров и β и в определении положения прямой по точкам Р (фактическим значениям). Зависимая переменная состоит из неслучайной и случайной составляющих.
Предположим, что мы нашли эти оценки и можно записать уравнение:
ŷ = a + bх,
где а - регрессионная постоянная, точка пересечения линии регрессии с осью OY;
b - коэффициент регрессии, угол наклона линии регрессии, характеризующий отношение YX;
ŷ - теоретическое значение объясняемой переменной.
Как известно в парной регрессии выбор вида математической модели может осуществляться тремя видами:
Графическим.
Аналитическим.
Экспериментальным.
Для выбора функции, описывающей наблюденные значения, можно использовать графический метод. Исходные данные наносятся на координатную плоскость. На оси абсцисс откладывают значения факторного признака, а на оси ординат - значения результирующего признака. Расположение точек покажет примерную форму связи. Как правило, эта связь является криволинейной. Если кривизна этой линии невелика, то можно принять гипотезу о существовании прямолинейной связи.
Функцию потребления изобразим в виде диаграммы рассеивания. Для этого в системе координат на оси абсцисс отложим значение дохода, а на оси ординат - расходы на потребление условно го товара. Расположение точек, соответствующих наборам значений "доход - расход на потребление", покажет пример ную форму связи (рисунок 1).
Визуально, по диаграмме, почти никогда не удаётся однозначно назвать наилучшую зависимость.
Перейдём к оценке параметров выбранной функции a и b способом наименьших квадратов.
Проблема оценивания может быть сведена к "классической" задаче отыскания минимума. Переменными теперь оказываются оценки а и b неизвестных параметров предполагаемой связи у и х. Для отыскания наименьшего значения какой-либо функции сначала надо найти частные производные I порядка. Затем каждую из них приравнять нулю и разрешить полученную систему уравнений относительно переменных. В нашем случае такой функцией является сумма квадратов отклонений - S, а переменными - а и b. То есть мы должны найти = 0 и = 0 и разрешить полученную систему уравнений относительно а и b.
Выведем оценки параметров по методу наименьших квадратов, предполагая, что уравнение связи имеет вид ŷ = a + bх. Тогда функция S имеет вид 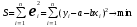 . Дифференцируя функцию S по а, мы получаем первое нормальное уравнение, дифференцируя по b - второе нормальное уравнение.
. Дифференцируя функцию S по а, мы получаем первое нормальное уравнение, дифференцируя по b - второе нормальное уравнение.
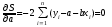 ,
,
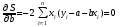 ,
,
После соответствующих преобразований получим:
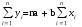
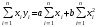 (*)
(*)
Существуют упрощенные правила построения системы нормальных уравнений. Применим их к линейной функции:
Перемножим каждый член уравнения ŷ = a + bх на коэффициент при первом параметре (а), то есть на единицу.
Перед каждой переменной поставим знак суммирования.
Свободный член уравнения умножим на n.
Получим первое нормальное уравнение
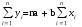
Перемножим каждый член исходного уравнения на коэффициент при втором параметре (b), то есть на х.
Перед каждой переменной ставим знак суммирования.
Получаем второе нормальное уравнение
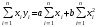
По этим правилам составляется система нормальных уравнений для любой линейной функции. Правила впервые были сформулированы английским экономистом Р. Перлом.
Параметры уравнений рассчитываются по следующим формулам:
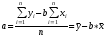 ,
,
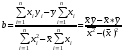 ,
,
Построим, используя исходные данные в таблице 1 , систему нормальных уравнений (*) и решим ее относительно неизвестных а и b:
1677=11*a+4950*b a = -3309
790 400=4950*a+2 502 500*b b = 7,6923
Уравнение регрессии имеет вид:
ŷ =-3309 + 7,6923 х,
Сравним фактические и расчетные расходы на потребление товара А (таблица 2).
Таблица 2 Сравнение фактических и расчетных значений расходов на потребление товара А при прямолинейной зависимости:
№ группы
Расходы на потребление
товара А
Отклонение фактических расходов от расчетных
фактические (у)
расчетные
(ŷ)
абсолютные
(у – ŷ)
1
120
-1770,54
1890,54
2
129
-1385,92
1514,92
3
135
-1001,31
1136,31
4
140
-616,45
756,45
5
145
-232,08
377,08
6
151
152,53
-1,53
7
155
537,15
-382,15
8
160
921,76
-761,76
9
171
1306,38
-1135,38
10
182
1690,99
-1508,99
11
189
2075,61
-1886,61
всего
-
-
0
Построим график полученной функции ŷ и диаграмму рассеивания, используя фактические значения (y) и расчётные (ŷ) .
Расчетные значения отклоняются от фактических в силу того, что связь между признаками корреляционная.
В качестве меры тесноты взаимосвязи используется коэффициент корреляции:
r = 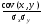 =
= 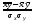
Получим, используя исходные данные из таблицы 1:
σx =158;
σy = 20,76;
r = 0,990.
Линейный коэффициент корреляции может принимать любые значения в пределах от минус 1 до плюс 1. Чем ближе коэффициент корреляции по абсолютной величине к 1, тем теснее связь между признаками. Знак при линейном коэффициенте корреляции указывает на направление связи - прямой зависимости соответствует знак плюс, а обратной зависимости – знак минус.
Вывод: связь между значениями х и соответствующими значениями у
тесная, прямая зависимость.
Кроме того, можно рассчитать коэффициент детерминации d, который равен квадрату коэффициента корреляции.
В нашем примере d = 0,9801
Это значит, что изменение расходов на товар А можно на 98,01 % объяснить изменением дохода.
Остальные 1,99 % могут явиться следствием:
недостаточно хорошо подобранной формы связи;
влияния на зависимую переменную каких-либо других неучтенных факторов.
Статистическая проверка гипотез.
Выдвигаем ноль-гипотезу о том, что коэффициент регрессии статистически незначим:
H0: b = 0.
Статистическая значимость коэффициента регрессии проверяется с помощью t-критерия Стьюдента. Для этого сначала определяем остаточную сумму квадратов
2ост=(yi – ŷi)2
2ост = 1,3689.
и ее среднее квадратическое отклонение
=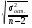
= 0,39.
Затем определим стандартную ошибку коэффициента регрессии по формуле:
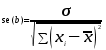
se(b) = 0,018.
Фактическое значение t-критерия Стьюдента для коэффициента регрессии:
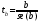 .
.
tb = 427,35.
Значение |tb|>tкр (tкр=2,26 для 95% уровня значимости) позволяет сделать заключение об отличии от нуля (на соответствующем уровне значимости) коэффициента регрессии и, следовательно, о наличии влияния (связи) х и у.
Вывод: фактическое значение t-критерия Стьюдента превышает табличное, значит ноль-гипотеза отклоняется и с вероятностью 95% принимается альтернативная гипотеза о статистической значимости коэффициента регрессии.
Далее построим 95% доверительный интервал для коэффициента регрессии b:
[b – tкр*se(b), b + tкр*se(b)]- 95% доверительный интервал для b.
Доверительный интервал накрывает истинное значение параметра b c заданной вероятностью (в данном случае 95%).
7,6516 < b < 7,7329.
Перейдем к проверке статистической значимости коэффициентов корреляции и детерминации:
r = 0,990;
d = r2 = 0,9801.
Выдвигаем ноль-гипотезу о том, что уравнение регрессии в целом статистически незначимо:
H0: r2 = 0.
Оценка статистической значимости построенной модели регрессии в целом производится с помощью F-критерия Фишера. Фактическое значение F-критерия для уравнения парной регрессии, линейной по параметрам определяется как:
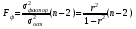
где 2фактор–дисперсия для теоретических значений ŷ (объясненная вариация);
2ост - остаточная сумма квадратов;
r2- коэффициент детерминации.
Фактическое значение F-критерия Фишера:
Fф = 443,26
Вывод: отклоняем ноль-гипотезу и с вероятностью 95% принимаем альтернативную гипотезу о статистической значимости уравнения регрессии.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ