Оперативно-производственное планирование на предметно-замкнутом участке

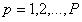
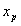
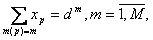
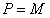
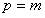
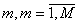
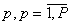
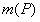
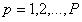
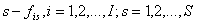
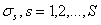
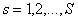
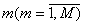
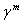
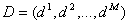
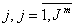
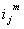
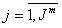
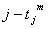
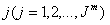
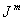
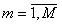
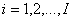
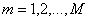
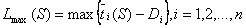
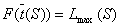
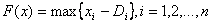
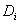
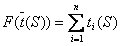
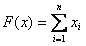
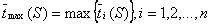
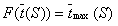
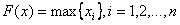
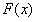
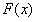
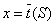
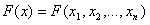
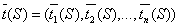
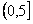
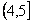
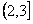
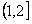
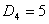
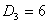
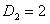
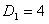
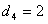
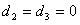
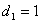
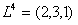
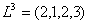
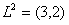
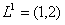
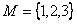
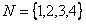
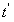
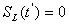
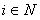
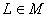
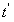
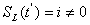
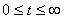
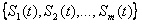
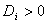
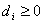
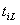
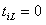
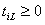
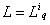
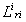
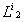
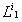
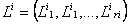
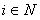
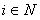
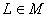
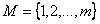
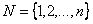
АВТОРЕФЕРАТ
Введение (актуальность темы)
Современное крупное машиностроительное предприятие является, как правило, весьма сложным по составу и взаимосвязям его производственных единиц — цехов. В настоящее время в машиностроении и в других отраслях промышленности все возрастающее значение приобретает комплексная автоматизация производства и управления.
Одним из важнейших методов исследования и построения системы управления промышленным предприятием является моделирование. Современная система управления заводом не может быть представлена без использования моделей как количественного основания принятия решения при организации, планировании и регулировании производства.
Под моделью понимается мысленно или материально созданная конструкция, воспроизводящая основные, наиболее существенные черты данного экономического явления. Модель отображает величины, определяющие характеристику данного хозяйственного процесса, воспроизводит его основные признаки и связи. Она не является полным описанием реальной экономической жизни во всей ее сложности, в ней опущены второстепенные, побочные элементы и свойства, не оказывающие на результат процесса существенного влияния.
Модели могут быть представлены графически, например, график функции двух переменных или сетевая модель управления сложным комплексом работ; в виде числовых моделей-матриц, таблиц численных значений переменных и их коэффициентов, аналитических выражений математических уравнений и др.
Независимо от вида модели, моделирование экономического процесса построено на представлении его в математическом виде. Математическая модель воспроизводит в количественной форме в виде соотношений (уравнений, неравенств, тождеств) качественные закономерности, существенные взаимосвязи хозяйственной деятельности.
Нередко процессы экономики и организации производства могут быть представлены в виде очень сложного математического аппарата, более того, для некоторых задач он может отсутствовать. Для построения моделей таких процессов используют системы искусственного интеллекта.
В управлении предприятием подсистема Оперативного Управления Предприятием (ОУП) занимает центральное место, поскольку является главной функциональной подсистемой АСУП, оказывающей наибольшее влияние на эффективность деятельности предприятия и служащей связующим звеном между всеми другими подсистемами АСУП. В задачи ОУП входит обеспечение ритмичной, равномерной работы предприятия по заранее разработанному графику. Основными особенностями задач ОУП являются: трудоемкость, громоздкость, необходимость получения результатов в короткие сроки, и др. Кроме того, самой природе производства свойственен элемент случайности (перевыполнение или нарушение плана по разным причинам), что требует корректировки составленного заранее плана.
По этому автоматизация ОУП позволит решить эти проблемы, и повысить основные показатели планирования.
Цель и задачи.
Разработать теоретические основы метода внутрицехового планирования; разработать программный модуль по автоматизации процесса внутрицехового планирования; провести опробирование программного модуля в условиях цеха машиностроительного предприятия.
Научная новизна.
До последнего десятилетия прошлого века в построении систем управления доминировал традиционный подход: линейные, нелинейные, адаптивные методы и др. Однако такой подход не всегда позволяет осуществлять робастное управление сложными нестационарными объектами. Данное обстоятельство послужило развитию нового научного направления – интеллектуальных систем управления.
Интеллектуальные системы управления – это системы управления, способные к “пониманию” и обучению в отношении объекта управления, возмущений, внешней среды и условий работы. Основное отличие интеллектуальных систем – наличие механизма системной обработки знаний. Главная архитектурная особенность, которая отличает интеллектуальные системы управления от традиционных, - это механизм получения, хранения и обработки знаний для реализации своих функций.
Существует несколько современных технологий, позволяющих создавать системы управления такого типа: экспертные системы, искусственные нейронные сети, нечеткая логика, генетические алгоритмы и ряд других. Интеллектуальные технологии между собой различает прежде всего то, что именно положено в основу концепции интеллектуальности – либо умение работать с формализованными знаниями человека (экспертные системы, нечеткая логика), либо свойственные человеку приемы обучения и мышления (искусственные нейронные сети и генетические алгоритмы).
Сегодня никто не отрицает, что многие широко известные методы тренировки искусственных нейронных сетей (ИНС) являются существенно локальными со всеми вытекающими отсюда последствиями. С другой стороны генетический алгоритм (ГА) высоко эффективен при решении задач глобальной оптимизации вообще и как потенциальная процедура тренировки нейронной сети, в частности. В этом отношении ГА не знают конкурентов. Таким образом, интригующим представляется само сочетание ГА и ИНС. Хотя в сочетании с ГА можно использовать один из традиционных методов локальной оптимизации, например градиентный.
Поэтому целью работы является реализация программного модуля на основе методов искусственного интеллекта, позволяющего эффективно выполнять внутрицеховое планирование.
Практическая ценность.
Это позволит на практике быстро и эффективно решать задачи оперативно-производственного планирования. Разработанный программный модуль позволит сократить затрату материальных и временных ресурсов на выполнение планирования производственного процесса, повысит качество обработки информации и качество результата обработки, исключив ошибки, связанные с человеческим фактором.
Методы исследований.
Оперативно – календарное планирование в технологических системах на основе теории расписаний
Качество функционирования современного производства во многом определяется решениями, принимаемыми на этапах календарного планирования и оперативного управления. Особенно это актуально в связи с созданием современных автоматизированных производств – гибких производственных систем (ГПС). Системы оперативно – календарного планирования современных производств строятся в том числе и на достижениях так называемой «теории расписаний».
Теория расписаний – это наука, занимающаяся исследованиями детерминированных обслуживающих систем на предмет оптимизации расписаний их функционирования.
Примеры таких систем:
цех, участок, на станках которых осуществляется обработка деталей;
ВУЗ, где преподаватели обучают студентов и т.д.
В любом случае имеется конечное множество требований (деталей, преподавателей и т.д.) и конечное множество приборов (станков, групп студентов и т.д.) .
Предполагается, что i – е требование на каждой стадии его обслуживания q (например, на каждой операции технологического процесса) может быть обслужено любым из приборов (но не более, чем одним одновременно). Предполагается также, что каждый прибор одновременно может обслуживать не более одного требования.
В теории расписаний рассматриваются различные системы обслуживания:
системы поточного типа, в которых каждое требование сначала обслуживается приборами первой группы , затем второй группы и т.д. пока не будет обслужено приборами последней r – ой группы;
системы с различными порядками (маршрутами) прохождения приборов требованиями и т.д.
В частности, в последних системах с последовательными приборами для каждого требования задается своя, специфическая для этого требования последовательность его обслуживания приборами. Требование i сначала обслуживается прибором , затем и т.д. пока не будет обслужено прибором . Последовательности обслуживания могут быть различными для разных требований и могут содержать повторение приборов.
В любом случае, если требование i на стадии q должно или может быть обслужено прибором , то предполагается заданной длительность его обслуживания прибором. Запись , как привило, означает, что по условию задачи требование i на стадии q прибором L не обслуживается.
Наряду с величинами могут быть заданы также: момент поступления требования i в систему; директивный срок , к которому необходимо завершить обслуживание требования.
Процесс функционирования обслуживающей системы может быть описан путем задания расписания (календарного плана, временного графика и т.п.).
Расписание – некоторая совокупность указаний относительно того, какие именно требования какими именно приборами обслуживаются в каждый момент времени.
Расписание рассматривается как совокупность кусочно–постоянных непрерывных слева функций, каждая из которых задана на интервале и принимает значения 0, 1, …, n.
Если (здесь i – номер требования), то в момент времени прибор обслуживает требование . Если , то в момент времени прибор L простаивает.
При задании расписания должны соблюдаться все условия и ограничение, вытекающие из постановки рассматриваемой задачи, т.е. расписание должно быть допустимым.
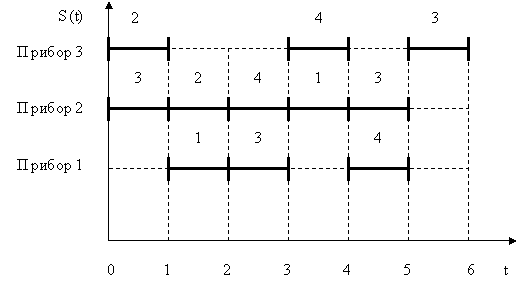
Пример. На рис.1 приведен график расписания обслуживания требований приборами при различных маршрутах обслуживания требований. Все длительности обслуживания равны «1».1
Рис.1. График расписания обслуживания требований N = {1, 2, 3, 4} приборами M = {1, 2, 3}
Здесь , т.е. первое требование обслуживается первым и вторым приборами, – второе требование обслуживается третьим и вторым приборами, – третье требование обслуживается вторым, первым, снова вторым и третьим приборами, - четвертое требование обслуживается вторым, третьим и первым приборами. – момент поступления требования 1 в систему, – моменты поступления требований 2 и 3 в систему, – момент поступления требования 4 в систему. – директивный срок завершения обслуживания требования 1, – директивный срок завершения обслуживания требования 2, – директивный срок завершения обслуживания требования 3, – директивный срок завершения обслуживания требования 4.
Прибор 1 во временном интервале обслуживает требование 1, в интервале - требование 3, в интервале - требование 4. Прибор 2 в интервале без простоев обслуживает требования 3, 2, 4, 1, 3 и т.д. Это расписание допустимо, т.е. каждый прибор одновременно обслуживает не более одного требования и i – е требование обслуживается одновременно не более, чем одним прибором.
Если существует несколько допустимых расписаний, то естественно необходимо выбрать лучшее из них. В теории расписаний качество расписания во многих случаях оценивают следующим образом. Каждое (допустимое) расписание S однозначно определяет вектор моментов завершения обслуживания требований. Задается некоторая действительная неубывающая по каждой из переменных функция . Качество расписания S оценивается значением этой функции при . Из двух расписаний лучшим считается то, которому соответствует меньшее значение . Расписание, которому соответствует наименьшее значение (среди всех допустимых расписаний), называется оптимальным.
В частности, при построении оптимального по быстродействию расписания . В этом случае , где .
При построении расписания с наименьшим суммарным временем обслуживания , при этом .
При построении расписания с наименьшим временем смещения моментов завершения обслуживания требований i относительно сроков функция . При этом , где .
Оптимальное расписание может быть найдено в результате перебора конечного множества возможных вариантов. Основная трудность при этом состоит в том, что число таких вариантов очень велико и растет, по меньшей мере, экспоненциально с ростом размерности задачи. Известны так называемые эвристические алгоритмы формирования расписаний, алгоритмы на основе методов линейного и динамического программирования. Задачи составления расписаний для некоторых сложных систем обслуживания до сих пор не решены (NP – трудные задачи).
Исходные данные для решения задачи:
1. Количество рассматриваемых видов деталей M. Виды деталей нумеруются числами .
2. Количество групп однотипного оборудования I. Группы оборудования нумеруются числами .
3. Технологические маршруты (ТМ) обработки деталей. ТМ не содержат внешних операций, т.е. операций, которые выполняются на другом оборудовании.
Для каждого вида деталей m () задаются:
количество операций в ТМ – , номера операций в ТМ обозначаются через ;
продолжительность обработки одной детали на операции (при обработке деталей m), ;
номер группы оборудования – , на котором выполняется операция .
4. План выпуска деталей различных видов – вектор .
5. Стоимость прол¨живания деталей вида в единицу времени.
Пусть отрезок планирования разбит на S частей, которые для простоты будем называть сутками и нумеровать числами . Для каждых суток должны быть заданы следующие величины:
6. Продолжительность суток .
7. Фонд времени групп оборудования i в сутки .
План выпуска деталей каждого вида разбивается на партии обработки. Обозначим число партий обработки P и введем для них единую нумерацию, не зависящую от вида деталей: . Будем считать известной функцию , которая по номеру партии дает номер вида детали (в частном случае, если запускается в обработку по одной партии каждого вида деталей, то и ).
Количество деталей в партии обработки p обозначим ; тогда должны иметь место равенства
(19.1)
т.е. сумма размеров всех партий для каждой детали равна плану ее выпуска.
Задача формулируется следующим образом: найти число партий обработки P, количество деталей в партиях обработки и расписания работы оборудования (обработки каждой партии), оптимальные с точки зрения некоторого критерия.
Эволюционные методы решениия NP-трудных задач
Эволюционные методы (ГА), как и ИНС, позволяют решать вспомогательные задачи теории управления, не привлекая такие базовые понятия, как интеграл, дифференциал, передаточная функция динамического звена и т.п.
В эволюционных методах вначале создается множество случайно сформированных объектов с заданной структурой (такое множество называется популяцией объектов) и функция, определяющая близость объекта к истинному решению, называемая функцией цены. Далее все эволюционные методы работают по общей схеме: определяется цена объектов в популяции, с учетом цены и при внесении элемента случайности создаются объекты для популяции следующей итерации. Данный процесс повторяется либо до получения решения, либо до окончания времени, отведенного на решение. Популяция имеет "память" - в ней накапливаются лучшие результаты предыдущих итераций, и этим эволюционные методы отличаются от других методов случайного поиска. В создании нового объекта популяции обычно участвуют два существующих объекта, от каждого из которых новый объект отбирает часть свойств; этот процесс называется скрещиванием или кроссинговером. При кроссинговере, кроме того, исходные объекты подвергаются некоторому случайному изменению - мутации. Иногда используется так называемая стратегия элитизма, при которой несколько лучших особей переходят в след поколение без изменений, не участвуя в кроссинговере и отборе.
Эволюционные методы представляют собой модель биологического процесса эволюции: в популяции идет борьба за существование; с течением времени объекты совершенствуются и выживают сильнейшие.
В литературе направление исследований, объединяющее различные эволюционные методы, получило название "эволюционные вычисления".
Рис.2. Основные операторы генетического алгоритма
(анимация - 8 циклов повторения)
Обычно все алгоритмы эволюционных вычислений состоят из следующих шагов:
Задается структура объектов, функция цены и условия останова
Создается популяция объектов Р
С помощью функции цены из популяции Р выбирается множество лучших объектов
С помощью операторов, поддерживающих эволюцию, из выбранных объектов создаются новые - претенденты на включение в следующую популяцию.
Образуется новая популяция Р из отобранных на 4-м шаге объектов.
Шаги 3-5 повторяются до выполнения условия останова.
Если итерации завершены успешно, то из итоговой популяции выделяется объект с высшей ценой, который является искомым решением. Иначе выдается сообщение о невозможности получить решение.
Объектами популяции могут быть структуры данных, автоматы, программы. Функция цены выбирается так, чтобы наибольшую цену имели объекты, лучше всего соответствующие целям эволюции.
Широкому распространению эволюционных вычислений способствует три причины.
Данные алгоритмы для многих типов задач показали свою эффективность по сравнению с другими методами.
Естественный отбор устраняет необходимость заранее учитывать все особенности решения задачи. Можно успешно решать задачи, структуру решения которых программист не знает. Существует много примеров решения с помощью эволюционных вычислений многих практических задач (задача коммивояжера, задачи распределения ресурсов; решение задач в реальном времени, связанных с управлением движущимися объектами).
Высокий параллелизм алгоритмов данного типа. Каждый объект популяции может обрабатываться независимо, что при применении мультипроцессорных компьютеров позволит достигать очень высоких скоростей работы.
Эволюционные методы целесообразно применять, если задачи трудно формализуемы или требуется быстро получить грубый результат для принятия решений в реальном времени.
Типичными представителями эволюционных вычислений являются: генетические алгоритмы, эволюционные стратегии и генетическое программирование.
Отличие генетических алгоритмов и эволюционных стратегий состоит в том, что, во первых, элементами популяций являются цепочки генов, а во вторых - действительные числа, являющиеся решениями задачи. Данные два направления очень близки между собой и иногда не различаются.
Заключение
Таким образом, оперативно-календарное планирование, которое составляет основу оперативного управления предприятием, очень трудоемкая задача. Ее решение имеет важное значение для работы всего предприятия. В традиционном подходе решения присутствуют существенные недостатки, поэтому в результате работы планируется получить новые методы, которые будут основываться на системах искусственного интеллекта, которые позволяют создавать более гибкие модели, чем методы статистической обработки информации.
Список использованной литературы
Усков А.А. Интеллектуальные технологии управления, М:Горячая линия – Телеком, 2004.
Егоров М.Е. Основы проектирования машиностроительных заводов, Высшая школа, 1969.
Егоров М.Е. Технология машиностроения, Высшая школа, 1976.
Мосталыгин Г.П. Технология машиностроения, Машиностроение, 1990.
Суслов А.Г. Научные основы технологии машиностроения, Машиностроение, 2002.
Каменицер С.Е. Автоматизированная система управления машиностроительным предприятием, Машиностроение, 1971.
Глушков В.М. Планирование дискретного производства в условиях АСУ”, Техника, 1975.
Соколицын С.А. Многоуровневая система оперативного управления ГПС в машиностроении, Политехника, 1991.
Смоляр Л.И. Модели оперативного планирования в дискретном производстве, Наука, 1978.
Шкурба В.В., и др. Планирование дискретного производства в условиях АСУ. Техніка, 1975.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ