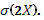
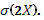
Алтайский Государственный Аграрный Университет

Индивидуальное задание по теории вероятности.

Тема: Элементы комбинаторики. Теоремы сложения и умножения вероятностей. Дискретная случайная величина.

Выполнила студентка 2 курса 725 группы Ищенко Юлия Проверила Миненко С.В.

Барнаул 2010

Задача №1.

Один из мальчиков родился в марте, а другой в апреле. Какова вероятность того, что оба они родились в первой неделе месяца?

Решение:

событие А – первый мальчик родился в первую неделю марта

событие В – второй мальчик родился в первую неделю апреля

Р=Р(А)*Р(В)

Р(А)=7/31 Р(В)=7/30 Р=7/31*7/30=0,05

Задача №2.

В компании «Стройпласт» 15 сотрудников, из них 9 бухгалтеров. Найти вероятность того, что среди 5, отправленных в командировку, окажется 3 бухгалтера.

Решение:

всего

бухг.

другие

Дано

15

9

6

берем

5

3

2

P(A)=m/n

n=C₁₅⁵=3003

m=C₉³*C₆²=1260

P(A)=1260/3003=0.42

Задача №3.

На пост директора фирмы выдвинуто 10 человек. Пусть вероятность того, что директором станет старший менеджер равна 0,6. Найти математическое ожидание и дисперсию числа старшего менеджера, ставшего директором.

Решение:

M(X)=np=10*0,6=6 D(X)=npq=10*0,6*0,4=2,4

Задача №4.

В компании «Стройком» работает 50 сотрудников. Не прошли аттестацию 9 человек. Найти относительную частоту непрошедших аттестацию.

Решение:

w(A)=m/n=9/50=0,18

Задача №5.

Даны независимые случайные величины.x_i – это значения Х, y_i – это значение У, а p_i – это их вероятности.

x_i

1

2

4

5

p_i

0,2

0,5

0,1

0,2

y_i

-1

0

2

3

p_i

0,4

0,3

0,2

0,1

Найти: М(Х+2У); D(3X - Y);

Решение:

1. М(Х)=0,2+1+0,4+1=2,6 М(2У)=2М(У)=0,6

М(У)=-0,4+0+0,4+0,3=0,3 М(Х+2У)=2,6+0,6=3,2

2. D(Х)=(1-2,6)²*0,2+(2-2,6)²*0,5+(4-2,6)²*0,1+(5-2,6)²*0,2=2,04

D(3X)=3²D(X)=18,36

D(У)=(-1-0,3)²*0,4+(0-0,3)²*0,3+(2-0,3)²*0,2+(3-,03)²*0,1=2,013

D(3Х-У)=18,36+2,013=20,373

3. D(2X)=2²D(X)=4*2,04=8,16

Задача №6.

В январе в отпуск собирается уйти 3 человека. Вероятности ухода первого, второго и третьего равны: р₁=0,5; р₂=0,2; р₃=0,9. Найти вероятность того, что в отпуск уйдет хотя бы один человек.

Решение:

Р(А)=1-0,5*0,8*0,1=0,96

Задача №7.

В организации 10 человек, из них 4 менеджера по продажам. На форум нужно отправить 3 человека. Найти вероятность того, что хотя бы один будет менеджер.

Решение:

всего

менедж.

другие

Дано

10

4

6

берем

3

1

2

или 2

или 1

или 3

или 0

А – хотя бы 1 менеджер

А₁ – 1 менеджер

А₂ – 2 менеджера

А₃ – 3 менеджера

Р(А)=Р(А₁)+Р(А₂)+Р(А₃) Р(А)=m/n

n=C₁₀³=120 m₁=C₄¹*C₆²=60; m₂=C₄²*C₆¹=36; m₃=C₄³*C₆⁰=4

Р(А₁)=0,5 Р(А₂)=0,3 Р(А₃)=0,03

Р(А)=0,5+0,3+0,03=0,83