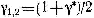
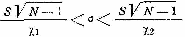
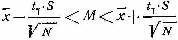
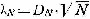
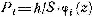
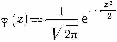
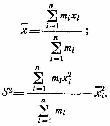
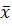
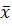
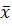
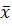Задание

номер интервала

границы интервалов t

частота m

свыше

до(включительно)

1

57,997

57,999

2

2

57,999

58,001

2

3

58,001

58,003

8

4

58,003

58,005

25

5

58,005

58,007

33

6

58,007

58,009

50

7

58,009

58,011

65

8

58,011

58,013

71

9

58,013

58,015

32

10

58,015

58,017

37

11

58,017

58,019

26

12

58,019

58,021

6

13

58,021

58,023

3

1. Определение теоретической функции плотности распределения. Графическое изображение эмпирического и теоретического распределений

плотность распределение доверительный математический ожидание

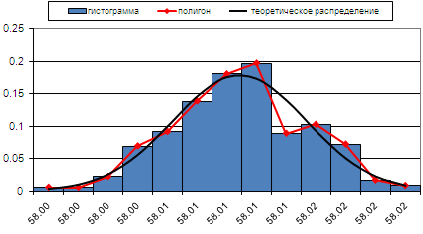
При построении гистограмм и полигонов по оси абсцисс откладывают значения результатов измерений (середины интервалов x_i), по оси ординат – частности появления результатов измерения в каждом i-м интервале.

Из-за ограниченности числа результатов измерений при обработке вместо математического ожидания и дисперсии получают их приближенные оценки– соответственно эмпирическое среднее и эмпирическую дисперсию S², характеризующие средний результат измерений и степень разброса измерений. и S² определяются из выражений:

Значения вероятности попадания результата измерения в конкретный интервал можно определить, используя значения функции:

,

где .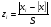

Тогда вероятность попадания результата в i-й интервал величиной h

.

Внесем все вычисления в таблицу и на основании полученных результатов построим кривую теоретического распределения, а так же гистограмму и полигон эмпирического распределения:

Середина интервала x_i

Эмпирич. частости P’_i

m_ix_i

x_i-

z_i

m_ix_i²

φ_i(z)

P_i

57,998

0,006

115,996

-0,01285

2,874965

6727,536

0,006399

0,002863

58

0,006

116

-0,01085

2,4275

6728

0,020956

0,009377

58,002

0,022

464,016

-0,00885

1,980034

26913,86

0,056179

0,025138

58,004

0,069

1450,1

-0,00685

1,532569

84111,6

0,123277

0,055162

58,006

0,092

1914,198

-0,00485

1,085103

111035

0,221427

0,099081

58,008

0,139

2900,4

-0,00285

0,637638

168246,4

0,325553

0,145674

58,01

0,181

3770,65

-0,00085

0,190173

218735,4

0,391793

0,175314

58,012

0,197

4118,852

0,00115

0,257293

238942,8

0,385954

0,172701

58,014

0,089

1856,448

0,00315

0,704758

107700

0,311212

0,139257

58,016

0,103

2146,592

0,00515

1,152223

124536,7

0,20541

0,091914

58,018

0,072

1508,468

0,00715

1,599689

87518,3

0,110976

0,049658

58,02

0,017

348,12

0,00915

2,047154

20197,92

0,049077

0,02196

58,022

0,008

174,066

0,01115

2,494619

10099,66

0,017765

0,007949

Сумма

20883,91

1211493

=

58,01085

S²=

1,99775E-05

S=

0,00446962

2. Критерий согласия эмпирического и теоретического распределений

Считают, что эмпирическое распределение хорошо согласуется с теоретическим, если (1 - ) больше 0,1. Согласно критерию Колмогорова, сравнивают эмпирические и теоретические значения, но уже не плотности распределения, а интегральной функции. Значение максимальной (по абсолютной величине) разности между ними D_N подставляют в выражение:

,

где N – объем выборки.

Вычисление эмпирических F’_i и теоретических F_i значений интегральной функции производим путем последовательного суммирования соответственно значений P’_i и P_i. Результаты вычислений сведены в таблицу:

Номер интервала

P_i

P’_i

F_i

F’_i

Fi-Fi'

1

0,002863

0,005556

0,002863

0,005556

0,002692

2

0,009377

0,005556

0,01224

0,011111

-0,00113

3

0,025138

0,022222

0,037379

0,033333

-0,00405

4

0,055162

0,069444

0,092541

0,102778

0,010237

5

0,099081

0,091667

0,191622

0,194444

0,002823

6

0,145674

0,138889

0,337295

0,333333

-0,00396

7

0,175314

0,180556

0,512609

0,513889

0,00128

8

0,172701

0,197222

0,68531

0,711111

0,025801

9

0,139257

0,088889

0,824566

0,8

-0,02457

10

0,091914

0,102778

0,91648

0,902778

-0,0137

11

0,049658

0,072222

0,966138

0,975

0,008862

12

0,02196

0,016667

0,988098

0,991667

0,003568

13

0,007949

0,008333

0,996048

1

0,003952

D_N= F'₈ – F ₈= 0,025801,

N=m_i=360,

Тогда получаем:

λ= 0,48953

Для _N=0,52   0,05  (1 – 0,05)=0,95 >0,1.

Отсюда можно сделать вывод: согласие эмпирического распределения с нормальным теоретическим можно считать хорошим.

3. Определение доверительных интервалов

В ряде задач, особенно при малом числе измерений, требуется не только найти эмпирическую оценку для того или иного параметра, но и определить доверительный интервал, в котором с доверительной вероятностью будет находиться теоретическое значение параметра.

Доверительный интервал для математического ожидания определяем из выражения:

интегральный доверительный интервал математический ожидание

Значения t_γ табулированы и равняется t_γ = 2,18 для N=13 и γ*=0,95.

58,00814756 58,01355244

Доверительный интервал для среднего квадратического отклонения определяем из выражения:

Значения χ₁², χ₂² табулированы и определяется в зависимости от числа измерений N и односторонних вероятностей γ₁, γ₂:

Значение χ₁² определяем при вероятности (1- γ₁), χ₂² – при γ₂.

χ₁²=24,1 χ₂²=4,18

И тогда

0,003024897

<σ<

0,008194587

4. Определение диапазона рассеивания значений

Определение границ диапазона рассеивания значений по результатам измерений, при вероятности риска 0,0027 .

М 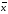 =58,01085

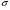 S =0,00446962

М-3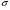 57.997442

М+3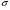 58.024258

Определение границ диапазона рассеивания значений по результатам измерений, при допускаемом значении вероятности риска 2β=0,001

М±σ

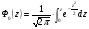
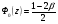
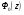=0,4995 при этом =3,29 (по справочнику)

М-3,29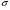=57,996146

М+3,29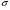=58,025554

Список использованной литературы

1. Зябрева Н.Н. и др. Пособие к решению задач по курсу "Взаимозаменяемость, стандартизация и технические измерения". Учеб. Пособие для вузов. М., "Высш. школа", 1977.