Интеграл дифференциального уравнения
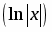
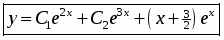

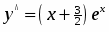
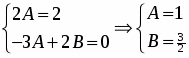
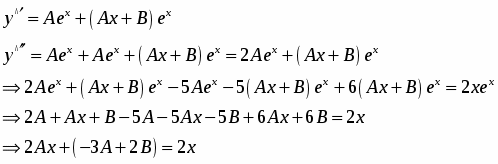
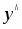
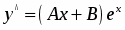
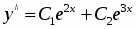
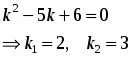
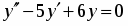
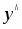
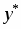
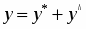
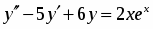
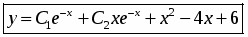
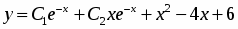
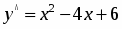
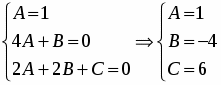
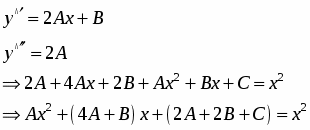
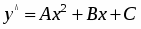
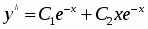
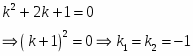
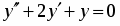
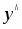
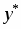
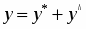
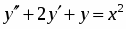
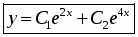
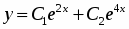
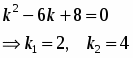
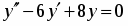
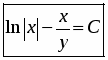
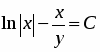
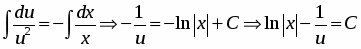
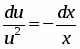
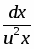
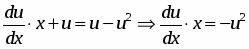
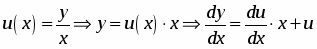
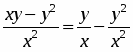
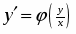
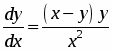
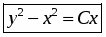
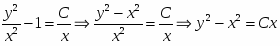
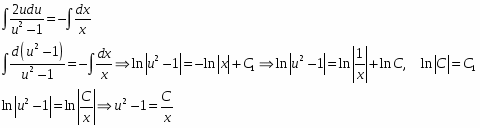
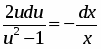
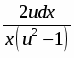
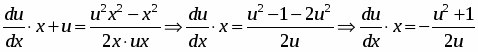
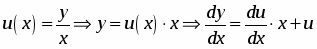
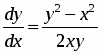
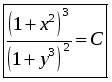
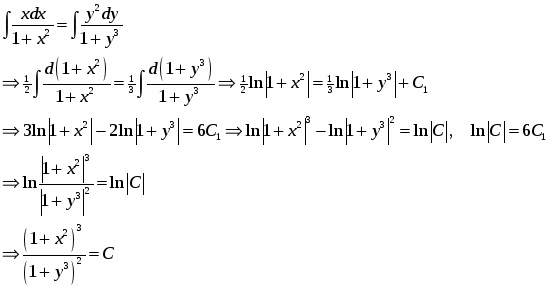
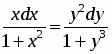
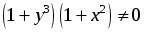
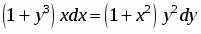
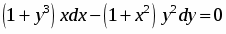 АНО ВПО «НАЦИОНАЛЬНЫЙ ИНСТИТУТ ИМЕНИ ЕКАТЕРИНЫ ВЕЛИКОЙ»
АНО ВПО «НАЦИОНАЛЬНЫЙ ИНСТИТУТ ИМЕНИ ЕКАТЕРИНЫ ВЕЛИКОЙ»
Контрольное задание
По дисциплине: «Математика»
Москва 2010 г.
Контрольное задание:
Упражнения
1. Дана последовательность аn=(3n-5)/(4n+1). Установить номер n0, начиная с которого выполняется неравенство │аn-А │ < 1/500.
Отв. n0=719.
Найти:
2. lim (3-√х)/(х2-81).Отв. –1/108.
х→9
3. lim (5х2-8)/(х3-3х2+11).Отв. 0.
х→∞
Проверить непрерывность следующих функций:
4. у=5х/(х3+8).Отв. При всех х≠–2 функция непрерывна.
5. у=(х2+4)/ √(х2-36). Отв. Функция непрерывна при всех значениях
│х│>6.
6. Определить точки разрыва функции у=(8х+2)/(16х2-1).
Отв. Точки х1=–1/4 и х2=1/4.
Задача 1
Найти общий интеграл дифференциального уравнения:
Решение
Выполним разделение переменных, для этого разделим обе части уравнения на :
Проинтегрируем обе части уравнения и выполним преобразования:
Ответ
Задача 2
Проинтегрировать однородное дифференциальное уравнение:
Решение
Решение однородных дифференциальных уравнений осуществляется при помощи подстановки:
,
С учетом этого, исходное уравнение примет вид:
Выполним разделение переменных, для этого умножим обе части уравнения на , получим,
Проинтегрируем обе части уравнения и выполним преобразования:
Возвращаясь к переменной y, получим общий интеграл исходного уравнения:
Ответ
Задача 3
Найти общий интеграл дифференциального уравнения:
Решение
Покажем, что данное уравнение является однородным, т.е. может быть представлено в виде, . Преобразуем правую часть уравнения:
Следовательно, данное уравнение является однородным и для его решения будем использовать подстановку,
С учетом этого, уравнение примет вид:
Выполним разделение переменных, для этого умножим обе части уравнения на ,
Проинтегрируем обе части уравнения,
Возвращаясь к переменной y, получим,
Ответ
Задача 4
Решить линейное дифференциальное уравнение:
Решение
Составим характеристическое уравнение и найдем его корни:
Так как корни характеристического уравнения действительные и различны, то решение дифференциального уравнения будет иметь вид:
Ответ
Задача 5
Найти общее решение дифференциального уравнения:
Решение
Общее решение неоднородного уравнения будем искать в виде:
,
где – частное решение исходного неоднородного ДУ, – общее решение соответствующего однородного уравнения:
Составим характеристическое уравнение и найдем его корни:
Так как корни характеристического уравнения действительные и совпадают, то общее решение однородного ДУ будет иметь вид:
Учитывая, что правая часть имеет специальный вид, то частное решение неоднородного уравнения будем искать в виде,
,
где A, B, C – неопределенные коэффициенты. Найдем первую и вторую производные по x от и подставим полученные результаты в исходное уравнение:
Приравняем коэффициенты при соответствующих степенях x и определим их:
Следовательно, частное решение неоднородного ДУ примет вид:
Окончательно, общее решение исходного ДУ:
Ответ
Задача 6
Решить уравнение:
Решение
Общее решение неоднородного уравнения будем искать в виде:
,
где – частное решение исходного неоднородного ДУ, – общее решение соответствующего однородного уравнения:
Составим характеристическое уравнение и найдем его корни:
Так как корни характеристического уравнения действительные и различны, то общее решение однородного ДУ будет иметь вид:
Учитывая, что правая часть имеет специальный вид, то частное решение неоднородного уравнения будем искать в виде,
,
где A, B, C – неопределенные коэффициенты. Найдем первую и вторую производные по x от и подставим полученные результаты в исходное уравнение:
Приравняем коэффициенты при соответствующих степенях x и определим их:
Следовательно, частное решение неоднородного ДУ примет вид:
Окончательно, общее решение исходного ДУ:
Ответ
Комментарии к решению
В задаче №1, опечатка в предполагаемом ответе, упущен показатель степени при x.
В задаче №3, ответ следует оставить в виде, содержащем модуль , т.к. нет достаточных оснований его снять.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ