Муниципальное бюджетное общеобразовательное учреждение «Фокинская средняя общеобразовательная школа № 2»

г. Фокино, Брянская область

Исследовательская работа по математике на тему:

«Простые числа - удивительные числа»

Автор работы: Беспокойная Елизавета, ученица 7 «Б» класса МБОУ «Фокинская СОШ №2»

Руководитель: Фетисова Елена Владимировна, учитель математики МБОУ«Фокинская СОШ №2»

г.Фокино

2012-2013

Оглавление

I. Введение…………………………………………………3- 4 стр.

II. Основная часть

1. Понятие простого числа………………………………………4 - 5 стр.

2. Из истории простых чисел……………………………………5 - 10 стр

3. Современные исследования…………………………………..10-11 стр

4. Свойства простых чисел………………………………………11-12 стр

III. Приложение……………………………………………………12–13 стр

IV. Заключение…………………………………………………… 14 стр

V. Источники информации………………………………………. 15 стр

1. Введение

«Среди чисел существует такое совершенство и согласие,

что нам надо размышлять дни и ночи

над их удивительной закономерностью».

Стевин

Простые числа с давних времен привлекают внимание математиков. Простые числа следует одно за другим по закону, который еще не найден. Но простые числа в математике играют важную роль.

С понятиями простого и составного чисел я впервые встретилась при изучении математики в 6 классе. Эта тема меня очень заинтересовала и я решила провести исследование по этой теме.

Проблемный вопрос: «Что же это за удивительные простые числа?».

Слово «простой» в толковом словаре русского языка С.И.Ожегова определяется как «однородный по составу, не составной; не сложный, не трудный, легко доступный пониманию, осуществлению».

В энциклопедии «Викисловарь»: «Значения слова «простой» -

 доступный и не требующий много времени и усилий для понимания, решения, выполнения, описания, использования;

 ничем не выделяющийся среди прочих, обыкновенный, типичный, стандартный;

 недорогой, без дополнительных функций, опций, аксессуаров, дополнительных этапов при производстве, ингредиентов и специй».

Немногие математические понятия настолько доступны далёкому от математики человеку, как понятие «простые числа». Любому встретившемуся на улице можно за короткое время объяснить, что такое простые числа. Поняв, человек без труда скажет: 2,3,5,7,11,13,17,… Так неужели эти числа так просты, понятны и доступны? Соответствуют ли они своему названию?

Итак, предметом исследования является простые числа.

Объект исследования: множество натуральных чисел.

Цель данной работы: изучение истории простых чисел и исследование некоторых свойств и видов простых чисел.

Для достижения этой цели перед собой поставила следующие задачи:

1. Собрать и изучить материал по этой теме.

2. Изучить исторические сведения о простых числах.

3. Открыть какие-либо закономерности и свойства в ряду чисел.

4. Изучить метод «Решето Эратосфена» для нахождения простых чисел.

Предлагаемая работа является результатом исследования множества простых чисел, проведенного по таблице простых чисел и по литературным источникам.

Основными методами являются сбор, изучение, анализ, обобщение исследовательского и теоретического материала, рефлексивное осмысливание результатов.

2. Основная часть

Всякий, кто изучает простые числа, бывает очарован ими

и одновременно ощущает собственное бессилие. Определение

простых чисел так просто и очевидно; найти очередное про-

стое число так легко; разложение на простые сомножите-

ли — такое естественное действие. Почему же тогда про-

стые числа столь упорно сопротивляютя нашим попыткам

постичь порядок и закономерность их расположения?

Ч. Уэзерелл.

1. Понятие простого числа.

Просто́е число́ — это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя.

Простые числа принадлежат множеству натуральных чисел. Евклид определял простые числа так: “Простое число есть измеряемое только единицей”. Иными словами, простые числа не имеют других делителей, кроме единицы и самого себя. Если p простое число, то его можно представить в виде произведения двух натуральных чисел только следующим образом: p = p*1. Числа, не являющиеся простыми, называются составными. Понятно, что всякое составное число имеет не меньше двух делителей отличных от 1.

Таким образом, простые числа – это как бы “кирпичики” для строительства всех натуральных чисел.

Число 1 не относится к простым числам. Математики предпочитают не считать 1 простым числом, поскольку в таком случае многие важные теоремы формулируются проще. Например, «основная теорема теории чисел» утверждает, что любое целое число допускает однозначное

(с точностью до порядка множителей) разложение на простые множители. Так число 100 представимо в виде произведения четырёх простых множителей 2*2*5*5. Всякий другой набор (отличающийся хотя бы одним числом) простых множителей не даст в произведении числа 100. Если же считать единицу простым числом, то эта весьма важная теорема неверна: число 100 в этом случае представимо в виде произведения бесконечно многих различных наборов простых чисел, например, в виде 2*2*5*5*1*1”.

Единственное чётное простое число 2. Все остальные простые числа нечётные, то есть любое простое число, отличное от 2, можно записать в виде: p = 2k + 1 (k ≥ 1).

Как и множество натуральных чисел, множество простых чисел бесконечно. Это доказал Евклид.

2. Из истории простых чисел

Простые числа и их свойства впервые активно начали изучать математики Древней Греции.

Математики школы Пифагора (500 г. до н.э. – 300 г. до н.э.) интересовались мистическими и нумерологическими свойствами чисел. Они понимали идею простоты чисел и изучали совершенные и дружественные числа.

Совершенное число – это число, которое равно сумме всех своих собственных делителей, т.е. делителей, отличных от самого числа. Например, число 6 имеет собственные делители 1,2 и 3, и 1+2+3=6, 28 имеет собственные делители 1, 2, 4, 7 и 14 , и 1+2+4+7+14=28.

Пара дружественных чисел – это пара таких чисел, как 220 и 284, собственные делители одного из них в сумме дают другое и наоборот.

Ко времени появления “Начал” Евклида, примерно в 300 г. до н.э., был доказан ряд важных результатов, касающихся простых чисел. В Книге IX “Начал” Евклид доказывает, что существует бесконечно много простых чисел. Это одно из первых известных доказательств, которое для того, чтобы установить результат, использует метод от противного. Евклид дает также доказательство основной теоремы арифметики: каждое целое число в сущности единственным способом можно представить в виде произведения простых чисел.

Евклид показал также, что если число 2ⁿ-1 простое, то число 2^{n -1}(2ⁿ-1) совершенное. Эйлеру (уже гораздо позже, в 1747 г.) удалось доказать, что все четные совершенные числа имеют такой вид. До сих пор неизвестно, существуют ли нечетные совершенные числа.

ок. 325 года до н.э.

Примерно в 200 г. до н.э. грек Эратосфен разработал алгоритм нахождения простых чисел, который называется решетом Эратосфена.

Алгоритм Эратосфена.

Пусть нам надо найти все простые числа в диапазоне от 1 до N. Выпишем подряд все числа от 2 до N. Зачеркнём в этом списке каждое второе число из следующих за числом 2. Таким образом мы отсеем все числа кратные числу 2. Число 2 является первым простым числом. Следующее не зачёркнутое число в списке после числа 2 – число 3. Это второе простое число. Повторим процедуру отсеивания, только теперь будем зачёркивать каждое третье число из следующих за числом 3. Так отсеем все числа кратные 3. Процедуру отсеивания следует повторять до тех пор, пока не доберёмся до простого числа, которое больше квадратного корня из N. Все числа, оставшиеся не зачёркнутыми в списке, будут простыми. Приведём иллюстрацию описанного метода для N = 50. Сначала покажем, как будет выглядеть список чисел после отсеивания чисел кратных 2:

2, 3, /4/, 5, /6/, 7, /8/, 9, /10/, 11, /12/, 13, /14/, 15, /16/, 17, /18/, 19, /20/, 21, /22/, 23, /24/, 25, /26/, 27, /28/, 29, /30/

31, /32/, 33, /34/, 35, /36/, 37, /38/, 39, /40/, 41, /42/, 43, /44/, 45, /46/, 47, /48/, 49, /50/

Примечание: зачёркнутые числа заключены в две наклонные черты / /.

Теперь покажем, как выглядит список после вычёркивания всех чисел кратных 3:

2, 3, /4/, 5, /6/, 7, /8/, /9/, /10/, 11, /12/, 13, /14/, /15/, /16/, 17, /18/, 19, /20/, /21/, /22/, 23, /24/, 25, /26/, /27/, /28/, 29, /30/

31, /32/, /33/, /34/, 35, /36/, 37, /38/, /39/, /40/, 41, /42/, 43, /44/, /45/, /46/, 47, /48/, 49, /50/

Осталось два этапа: вычеркнуть все числа кратные 5 и кратные 7. Окончательно получим такой список простых чисел (простые числа выделены красным цветом):

2, 3, /4/, 5, /6/, 7, /8/, /9/, /10/, 11, /12/, 13, /14/, /15/, /16/, 17, /18/, 19, /20/, /21/, /22/, 23, /24/, /25/, /26/, /27/, /28/, 29, /30/

31, /32/, /33/, /34/, /35/, /36/, 37, /38/, /39/, /40/, 41, /42/, 43, /44/, /45/, /46/, 47, /48/, /49/, /50/

В этом примере процедура отсеивания (зачёркивания) завершилась на простом числе 7, то есть последний раз мы зачёркивали в этом списке каждое седьмое число, следующее за числом 7. Числа кратные 11 мы уже не будем зачёркивать (отсеивать), так как это число больше квадратного корня из 50.

Во времена Эратосфена писали на восковых дощечках, а вместо того, чтобы числа зачёркивать, дощечку в нужном месте прокалывали. Отсюда и произошло название способа – “решето Эратосфена”: составные числа как бы “просеивались” в проколотые дырки, а простые числа оставались в “решете”.

Далее в истории простых чисел долгий застой в то время, которое обычно называют Темными веками Средневековья.

Следующие важные достижения были сделаны Ферма в начале XVII века. Он доказал гипотезу Альбера Жирара, что каждое простое число вида 4n+1 единственным образом представимо в виде суммы двух квадратов и смог показать, как любое число может быть представлено в виде суммы четырех квадратов. Он разработал новый метод факторизации больших чисел, который продемонстрировал на примере числа 2027651281=44021*46061 . Он доказал теорему, которая стала известна как малая теорема Ферма (чтобы отличить ее от его так называемой последней, или большой теоремы)

Пьер Ферма (1601 – 1665)

Работы Эйлера оказали большое влияние на теорию чисел в целом и на теорию простых чисел в частности.

Он обобщил малую теорему Ферма и ввел функцию Эйлера. Он разложил на множители пятое число Ферма, обнаружил 60 пар дружественных чисел, определенных ранее, и предположил (но не смог доказать) то, что стало известно как квадратичный закон взаимности.

Эйлер был первым, кто понял, что теория чисел может изучаться с помощью инструментов анализа, и, таким образом, положил начало аналитической теории чисел.

Леонард Эйлер (1707 – 1783)

На первый взгляд кажется, что простые числа распределены между целыми числами случайным образом. Например, среди 100 чисел непосредственно предшествующих числу 10 000 000, есть 9 простых чисел, а в 100 числах сразу же после 10 000 000 – только 2 простых числа. Однако в больших масштабах простые числа распределены довольно регулярно. Лежандр и Гаусс выполнили большие расчеты плотности расположения простых чисел. Гаусс (который был мощным вычислителем) рассказал другу, что всякий раз, когда у него было свободных 15 минут, он проводил их, вычисляя простые числа в “тысяче” (диапазоне в 1000 чисел). К концу своей жизни, по оценкам, он нашел все простые числа примерно до 3 000 000.

В 1837 г. немецкий математик Л. Дирихле доказал, что в любой арифметической прогрессии, первый член и разность которой взаимно просты, есть бесконечно много простых чисел.

В 1852 г. П. Л. Чебышев доказал предположение французского математика Ж. Бертрана о том, что для любого натурального числа N между числами N и 2N всегда есть простое число.

Среди простых чисел особую роль играют простые числа Мерсенна – числа вида М_р=2^р-1. Они называются простыми числами Мерсенна по имени французского монаха Мерена Мерсенна (1588-1648), одного из основателей Парижской Академии наук.

Так как М₂=2²-1=3 т.е. М₂=3, М₃=7, М₅=31, М₇=127, то это – простые числа Мерсенна. До 1750 года было найдено всего 7 простых чисел Мерсенна: М_2, М_3, М_5, М₇, М_13, М₁₇, М₁₉ . То что М₃₁ – простое число, оказал в 1750 году Л.Эйлер. В 1876 году французский математик Эдуард Люка установил, что число

М₁₂₇=170141183460469231731687303715884105727 – простое. В 1883 г. Сельский священник Пермской губернии И.М.Первушин без всяких вычислительных приборов доказал, что число М₆₁= 2305843009213693951 является простым. Позднее было установлено, что числа М₈₉ и М₁₀₇ – простые. Использование ЭВМ позволило в 1952-1964 годах доказать, что числа М₅₂₁, М₆₀₇, М₁₂₇₉, М₂₂₀₃, М₂₂₈₁, М₃₂₁₇, М₄₂₅₃, М₄₄₂₃, М₂₆₈₉, М₉₉₄₁, М₁₁₂₁₃- простые. К настоящему времени известно уже более 30 простых чисел Мерсенна.

3.Современные исследования

Наибольшее известное простое число (найдено GIMPS [Great Internet Mersenne Prime Search] в августе 2008 года) было 45-м числом Мерсенна – M_43112609, которое состоит из 1209780189 десятичных цифр. Совсем недавно было обнаружено новое простое число Мерсенна (сентябрь 2008) M_37156667.

Самые большие известные простые числа-близнецы – это 2003663613*21950001. Они состоят из 58711 цифр, и были объявлены Вотье, Мак-Киббоном и Грибенко в 2007 году.

Наибольшее известное факториальное простое число (простое число вида n!1) –это 34790!. Это число содержит 142891 цифр и было объявлено Маршалем, Кармоди и Куоса в 2002 году.

Наибольший известный простой примориал (простое число вида n#1, где n#1– произведение всех простых чисел <1) – это 392113#1+1 . Это число состоит из 169966 цифр и было объявлено Хоером (Heuer) в 2001 году.

Современные компьютеры помогают находить большие простые числа, но их возможности тоже ограничены, так как множество простых чисел бесконечно.

С помощью ЭВМ найдено самое большое простое число Мерсенна

2 р -1 при р = 216091.

Самые большие известные числа-близнецы

1 000 000 009 649 и 1 000 000 009 651.

Нет пока ответа на вопрос о том, существует ли самая большая пара чисел-близнецов.

Количество простых чисел на отрезке натурального ряда от 1 до N очень быстро возрастает с увеличением N:

N

Количество простых чисел

%

102

25

25

104

1 229

12,3

106

78 498

7,8

108

5 761 455

5,8

1010

455 052 511

4,6

1012

37 607 912 018

3,8

1014

3 204 941 750 802

3,2

1016

279 238 341 033 925

2,8

4.Свойства простых чисел.

1.Два простых числа, которые отличаются на 2, как 5 и 7, 11 и 13, 17 и 19 и т.д. получили образное название «близнецы». До сегодняшнего дня не решено конечные числа «близнецов»

2. Три числа, которые отличаются на 2, называются «тройняшками», 3, 5, 7.

3. 168 мест первой тысячи натуральных чисел занимают простые числа. Из них 16 чисел – палиндромические – каждое равно обращённому. Например: 11,101, 131, 151, 181, 191, 313, 353, 373, 383, 727, 757, 787, 797, 919, 929 и т.д.

4. Симметричные себе простые числа: 107 – 701, 113 – 311, 149 – 941,

157 – 751, 167 – 761, 179 – 971, 199 -991, 337- 733, 347 – 743,

359 – 953, 389 – 983, 709 – 907, 739 -937, 769 – 967

5. Простые числа могут разместиться в магическом квадрате (Магические (волшебные) квадраты – квадратные таблицы натуральных чисел (с одинаковым количеством строк и столбцов), имеющие одну и ту же сумму чисел по всем строкам, столбцам и диагоналям).

571

1051

181

211

601

991

1021

151

631

И

823

1093

643

673

853

1033

1063

613

883

6. Любое четное число, больше 2, можно представить в виде суммы 2-х простых чисел.

Например: 4=2+2, 6=3+3, 8=5+3, 10=3+7, 12=5+7,, 14=7+7, 16=11+5, 18=7+11,, 20=3+17, 56=19+37, 924=311+613 и т.д. Но это утверждение не доказано. Такую задачу называют проблемой Варинга

7. Любое нечетное число больше 5, можно представить в виде суммы трех простых чисел.

Например: 7=2+3+2, 9=2+5+2, 11=5+3+3, 13=5+5+3, 15=7+5+3, 17=5+5+7, 19=5+7+7, 21=3+7+11, 23=5+7+11, 25=17+3+5 и т.д.

Подойти к доказательству этого предложения сумел лишь 200 лет спустя русский математик, академик Иван Матвеевич Виноградов (1891-1983).

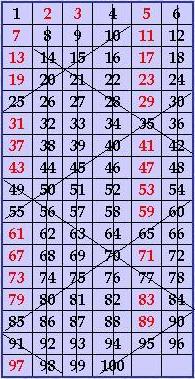
3. Приложение

Нахождение простых чисел с помощью решета Эратосфена

от 1 до 100.

Решето Эратосфена (диагональное)

1.Выпишем все целые числа от 1 до 100 в виде прямоугольной таблицы.

2.Вычеркнем 1, которая не является ни простым, ни составным числом.

3.Вычеркнем все числа, кратные 2 (за исключением самой 2), проведя вертикальные черты во втором, четвертом и шестом столбцах.

4.Вычеркнем все числа, кратные 3, (за исключением самой 3), проведя вертикальную черту в третьем столбце. Следующее за 3 не вычеркнутое число равно 5.

5.Чтобы вычеркнуть все числа, кратные 5, проведем диагонали, идущие вниз и влево.

6.Чтобы вычеркнуть все числа, кратные 7, проведем диагонали, идущие с наклоном вправо и вниз.

7.Числа 8,9 и 10 – составные, их кратные уже были вычеркнуты раньше.

Следующее простое число 11, 11∙11=121. Если бы таблица была больше, то пришлось бы исключать кратные 11, проводя диагонали с более крутым наклоном. И так далее…

Все не зачёркнутые числа в таблице на рис., кроме числа 1, являются простыми (они выделены красным цветом).

4. Заключение

До сих пор математики тщетно пытались обнаружить в по-

следовательности простых чисел какой-либо порядок, и мы

имеем все о снования верить, что здесь существует какая-

то тайна, в которую человеческий ум никогда не проникнет.

Л.Эйлер.

В своей работе «Простые числа - удивительные числа» изучена история, свойства простых чисел.

Я сделала следующие выводы:

1. Можно сказать, что простые числа представляют собой как бы кирпичики, из которых строятся все остальные числа.

2. Для простых чисел не существует формулы, по которой их можно вычислить.

3. Не существует самого большого простого числа, последовательность простых чисел бесконечна.

4. Многие ученые на протяжении многих веков вносили свой вклад в изучение темы «Простые числа».

5. Простые числа не совсем соответствуют значениям и определению слова «простой». По своей сути они очень сложны, многогранны и хранят много тайн, неизвестного.

6. В настоящее время исследование темы продолжается, ученые делают, и будут делать новые открытия!

«Все вопросы, зависящие от закона распределения простых

чисел в ряду 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, . . . ,

представляют вообще большие трудности. Те заключения,

которые можно сделать с очень большой вероятностью на

основании таблиц простых чисел, чаще всего остаются без

строгого доказательства» - П. Л. Чебышёв.

Список использованной литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 класс. Учебник для общеобразовательных учреждений-М; «Мнемозина», 2011г.

2. Карпеченко Е. Тайны чисел .Математика / Прил. К газете "Первое сентября" №13 2007.

3. Крылов А.Н. Числа и меры. Математика / Прил. К газете "Первое сентября"№7 1994

4. Ожегов С.И., Шведова Н.Ю. Толковый словарь русского языка 3-е изд., стереотипное-М; «АЗЪ», 1996г.

5. Энциклопедический словарь юного математика. Сост. А.П.Савин. – М.: Педагогика, 1989.

Интернет-ресурсы

1. http://ru.wikipedia.org/wiki/Простое_число

2. http://www.natalimak1.narod.ru/prost.htm

3. http://www.tinlib.ru/matematika/priglashenie_v_teoriyu_chisel/p4.php

4. http://ru.math.wikia.com/wiki/Простое_число