Никитина Валентина Николаевна

учитель математики

МБОУ «СОШ №18»,

статья

«Некоторые особенности развития ключевых компетенций учащихся на уроках алгебры и начал анализа в процессе изучения обратных тригонометрических функций на профильном уровне»

математика

10-11 классы

Некоторые особенности развития ключевых компетенций учащихся на уроках алгебры и начал анализа в процессе изучения обратных тригонометрических функций на профильном уровне.

Согласно концепции модернизации российского образования среднее (общее) образование нацелено на формирование ключевых компетенций школьников. По мнению разработчиков новых стандартов, введение компетенций в нормативную и практическую составляющую образования позволит решить проблему российской школы, когда учащиеся, получив знания, испытывают трудности в применении этих знаний для решения конкретных жизненных задач и проблемных ситуаций. Что же такое ключевые компетенции? Под ключевыми компетенциями понимается целостная система не только универсальных знаний, умений, навыков, но и опыт самостоятельной деятельности, а также личной ответственности обучающихся.

К ключевым компетенциям, по мнению российских исследователей ученых: В.А. Болотова, А.В.Хуторского, Б.Д. Эльконина и других относятся следующие группы ключевых компетенций:

• ценностно-смысловые компетенции, связанные с ценностными ориентирами учащегося, способностью видеть, понимать и ориентироваться в окружающем мире, уметь выбирать целевые и смысловые установки для своих действий и поступков, принимать решения, самоопределяться в ситуациях учебной и иной деятельности. От ценностно-смысловых компетенций зависит индивидуальная образовательная траектория ученика, его программа жизнедеятельности;

• общекультурные компетенции, связанные с познанием и опытом деятельности в области национальной и общечеловеческой культуры; с духовно-нравственными основами жизни человека и человечества, отдельных народов; с культурологическими основами семейных, социальных, общественных традиций и явлений; с ролью науки и религии в жизни человека; с компетенциями в бытовой и культурно - досуговой сфере деятельности;

• информационные компетенции, как навыки владения современными средствами информации и информационными технологиями; поиск, анализ и отбор нужной информации, умением её преобразовывать, сохранять и предавать;

• коммуникативные компетенции, связанные не только со знанием языков, способов взаимодействия с окружающими удалёнными событиями и людьми, но и навыками работы, как в группе, так и в большом коллективе и овладении различными социальными ролями;

• социально-трудовые компетенции – владение знаниями прав и обязанностей в вопросах экономики, права, в области профессионального самоопределения (умения анализировать ситуацию на рынке труда, владеть этикой трудовых и гражданских взаимоотношений);

• компетенции личностного самосовершенствования направлены на саморазвитие учащегося, как физического, духовного, интеллектуального, так и эмоциональной самоподдержки и саморегуляции (правила личной гигиены, забота о собственном здоровье, половая грамотность, внутренняя экологическая культура, способы безопасной жизнедеятельности);

• учебно-познавательные компетенции, как совокупность компетенций учащегося в сфере учебно-познавательной деятельности (логической, методологической, общеучебной), в учебно-познавательные компетенции входят способы организации целеполагания, планирования, анализа, рефлексии, самооценки. По отношению к изучаемым объектам ученик овладевает креативными навыками: добыванием знаний непосредственно из окружающей действительности, владением приемами учебно-познавательных проблем, действий в нестандартных ситуациях. В рамках этих компетенций определяются требования функциональной грамотности: умение отличать факты от вымыслов, владение измерительными навыками, использование вероятностных, статистических и иных методов познания.

Вместе с тем сегодня стало ясно, что ключевые компетенции представляют собой многоплановые и многоструктурные характеристики, оценка которых не может быть в полной мере стандартизирована. Они тяжело поддаются измерениям. Тем важнее сегодня разработка новых подходов к развитию ключевых компетентностей и оценки их сформированности у учащихся. Компетенция не сводится только к знаниям или только к умениям. Компетенция является сферой отношений, существующих между знанием и действием в практике.

Учебно-познавательные компетенции на уроках математики предполагают формирование у учащихся следующих умений и соответствующих им действий:

1. ставить цель и организовывать её достижение, уметь пояснить свою цель;

2. организовывать планирование, анализ, рефлексию, самооценку своей учебно-познавательной деятельности;

3. задавать вопросы к наблюдаемым фактам, отыскивать причины явлений, обозначать свое понимание или непонимание по отношению к изучаемой проблеме;

4. ставить познавательные задачи и выдвигать гипотезы; владеть измерительными навыками, работать с инструкциями; использовать элементы вероятностных и статистических методов познания; описывать результаты, формулировать выводы;

5. выступать устно и письменно с результатами своего исследования, используя компьютерные средства и технологии (текстовые и графические редакторы, презентации).

Рассматривая старшую ступень обучения математике, мы будем говорить о дальнейшем развитии учебно-познавательных, ценностно-смысловых, коммуникативных и информационных компетенций.

Содержание учебного предмета «Алгебра и начала анализа» содержит в себе возможности формирования познавательных компетенций, в частности ставит цель и организует не только её достижение, но и рефлексию и самооценку своей учебно-познавательной деятельности. При повторении понятия «обратные функции», учащиеся применяют ранее изученный материал, анализируют, систематизируют свои знания и умения по данной теме. При построении и чтении графиков «кусочных» функций, содержащих обратные тригонометрические функции, учащиеся также опираются на знания и умения, полученные в курсе алгебры за 7-9 классы, применяя их в новой, более сложной ситуации. Исследуя обратные тригонометрические функции на четность и нечетность, учащиеся продолжают приобщаться к законам формальной логики. Вторым основным каналом формирования учебно-познавательных компетенций является определённая организация учебной деятельности учащихся. В ходе выстраивания учебного процесса увеличивается количество и качество освоенных учеником элементов компетенций, происходит изменение и расширение объектов, компетенции интегрируются, взаимодействуют между собой, образуя комплексные новообразования личности.

Так одним из важных разделов курса алгебры и начал анализа является раздел «Тригонометрические функции» и в рамках этого раздела изучаются «Обратные тригонометрические функции».

В учебных пособиях для профильной школы: «Алгебра и начала анализа» под редакцией А.Г. Мордковича, «Алгебра и начала математического анализа» под редакцией С.М. Никольского и «Алгебра и начала математического анализа» под редакцией М.Я. Пратусевича данная тема представлена по-разному. Так в учебнике А.Г. Мордковича за 10 класс темой «Обратные тригонометрические функции» заканчивается глава «Тригонометрические функции», на изучение этой темы отводится от 3 до 5 учебных часов. При изучении темы учащиеся знакомятся с понятиями «обратимость функций», «обратная функция», алгоритмом построения графика обратной функции, учатся находить область определения и область значений обратной функции. Всё это рассматривается в главе «Числовые функции» в течение 2-4 уроков в начале учебного года. Поэтому за отведённое, на изучение темы «Обратные тригонометрические функции» время, приобретённые учащимися знания, умения и навыки по темам: «Обратные функции», «Тригонометрические функции», применяются уже на уровне приобретённых компетенций. Знакомство с функциями вида y=arcsinx, y=arccosx, y=arctgx и y=arcctgx их свойствами и графиками позволяет ввести понятия arcsin, arccos,arctg, arcctg. В названном учебнике рассматриваются также и преобразования выражений, содержащих обратные тригонометрические функции. Шестьдесят два, различных по уровням сложности, по объёму и содержанию упражнения, позволяют в полной мере понять и усвоить тему «Обратные тригонометрические функции». Приоритетная функционально-графическая линия курса алгебры и начал анализа в данном учебнике чётко выдержана и после изучения обратных тригонометрических функций, учащиеся знакомятся с простейшими тригонометрическими уравнениями.

В учебнике С.М. Никольского тема «Обратные тригонометрические функции» изучается в 11 классе в главе «Функции. Производные. Интегралы». Тригонометрические формулы и функции, тригонометрические уравнения и неравенства уже изучены учащимися в 10 классе. В 11 же классе после введения понятий «обратная функция», «взаимно обратные функции», изучаются обратные тригонометрические функции и рассматриваются примеры использования этих функций. Восемь упражнений, представленных в учебнике С.М. Никольского на данную тему, шесть из которых, первого и второго уровня сложности, только два упражнения соответствуют третьему уровню сложности. То есть по сравнению с предыдущим учебником упражнений немного, но они разного объёма и содержания, то есть комплексные, и тем самым дают достаточное представление об обратных тригонометрических функциях, относящихся к основным элементарным функциям.

В учебнике М.Я. Пратусевича «Алгебра и начала математического анализа» обратные тригонометрические функции изучаются в главе «Тригонометрия» в теме «Тригонометрические функции». На изучение темы «Тригонометрические функции» отводится 4 часа.

Фокин Ю.Г. в книге «Теория и технология обучения: деятельностный подход.» задаёт такой вопрос: «Как у ученика возникают знания и происходит его развитие?» и, разъясняя специфику деятельностного подхода, старается ответить на поставленный вопрос: «из всего разнообразного содержания того, чему учат и в школах, и в практической жизни, центральным звеном оказывается действие». Так «одним из средств вовлечения в учебную деятельность» учащегося «являются опорные сигналы», которые соединяют понятийное и образное, являющееся одним из источников интенсификации обучения и «основные компоненты организации учебной деятельности» учащихся:

• контроль усвоения темы (оценка уровня сформированности умений);

• обучение приёмам чтения учебной литературы;

• ведение словарей новых терминов, конспектов с формулировками теорем и их доказательствами;

• использование опорных сигналов для систематизации и запоминания учебного материала;

• организация познавательного общения;

• обучение формам коллективной познавательной деятельности (сочетание различных видов групповой и индивидуальной форм деятельности).

А развитие и формирование учебно-познавательных компетенций как раз и подразумевает такие действия как умение ставить, организовывать, планировать, выступать, анализировать свою деятельность.

Как же можно строить процесс развития учебно-познавательных компетенций на уроках алгебры и начал анализа при изучении темы «Обратные тригонометрические функции»? На наш взгляд, наиболее продуктивным является использование на уроках, при организации самостоятельной учебно-познавательной деятельности учащихся, следующих методических приёмов:

• решение одной и той же задачи несколькими способами;

• использование сравнения, в ходе которого учащиеся выявляют сходство и различия в изучаемой теме;

• анализ типичных ошибок, допускаемых в процессе решения задач;

• обучение с использованием элементов историзма.

А также технологизации учителем учебного процесса, например: применение элементов деятельностной, проективной, модульной технологий.

Приведём некоторые примеры, иллюстрирующие сущность предлагаемых рекомендаций. Как, например можно использовать приём сравнения?

Cведём определения arcsinx, arccosx, arctgx, arcctgx в таблицу

Характери-

стика

α = arcsinx

α = arccosx

α = arctgx

α = arcctgx

определение

sinα = x

cosα = x

tgα = x

ctgα =x

Область определения

x

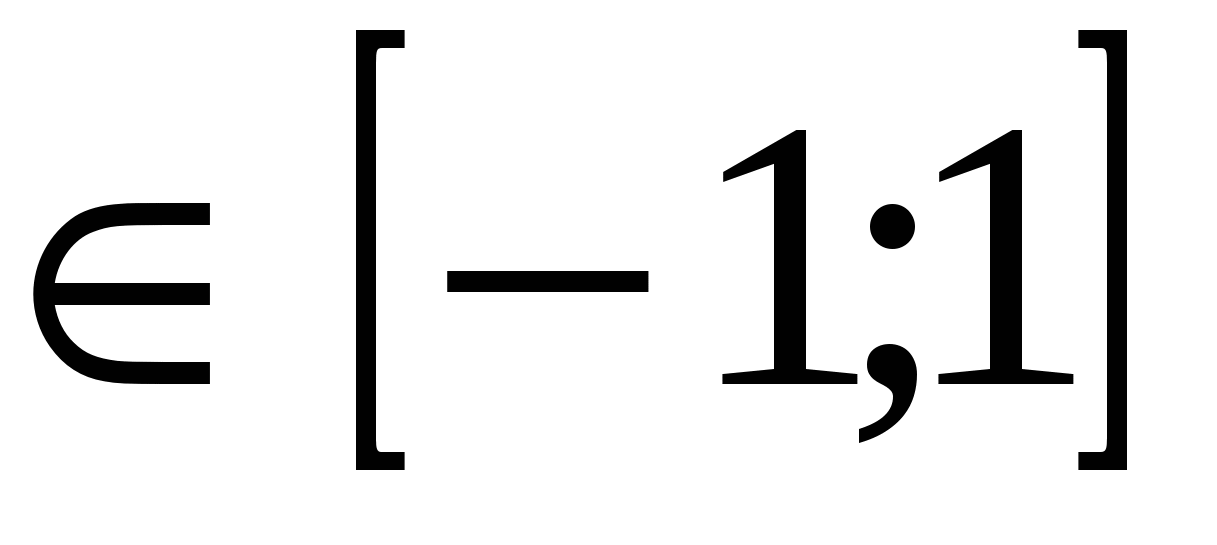
x

(-∞;∞)

(-∞;∞)

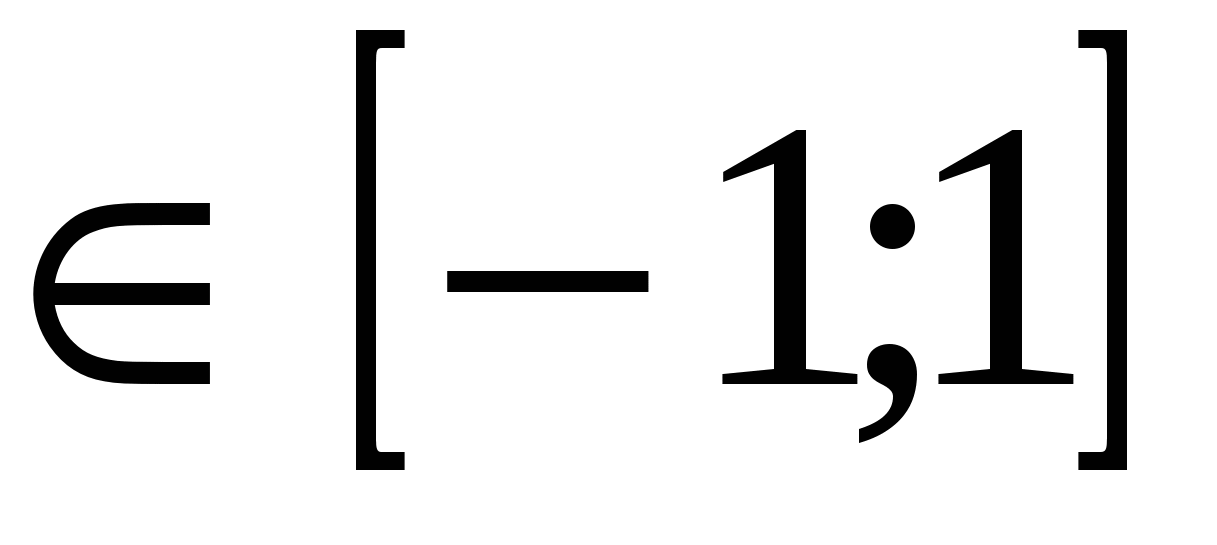
Множество значений

α

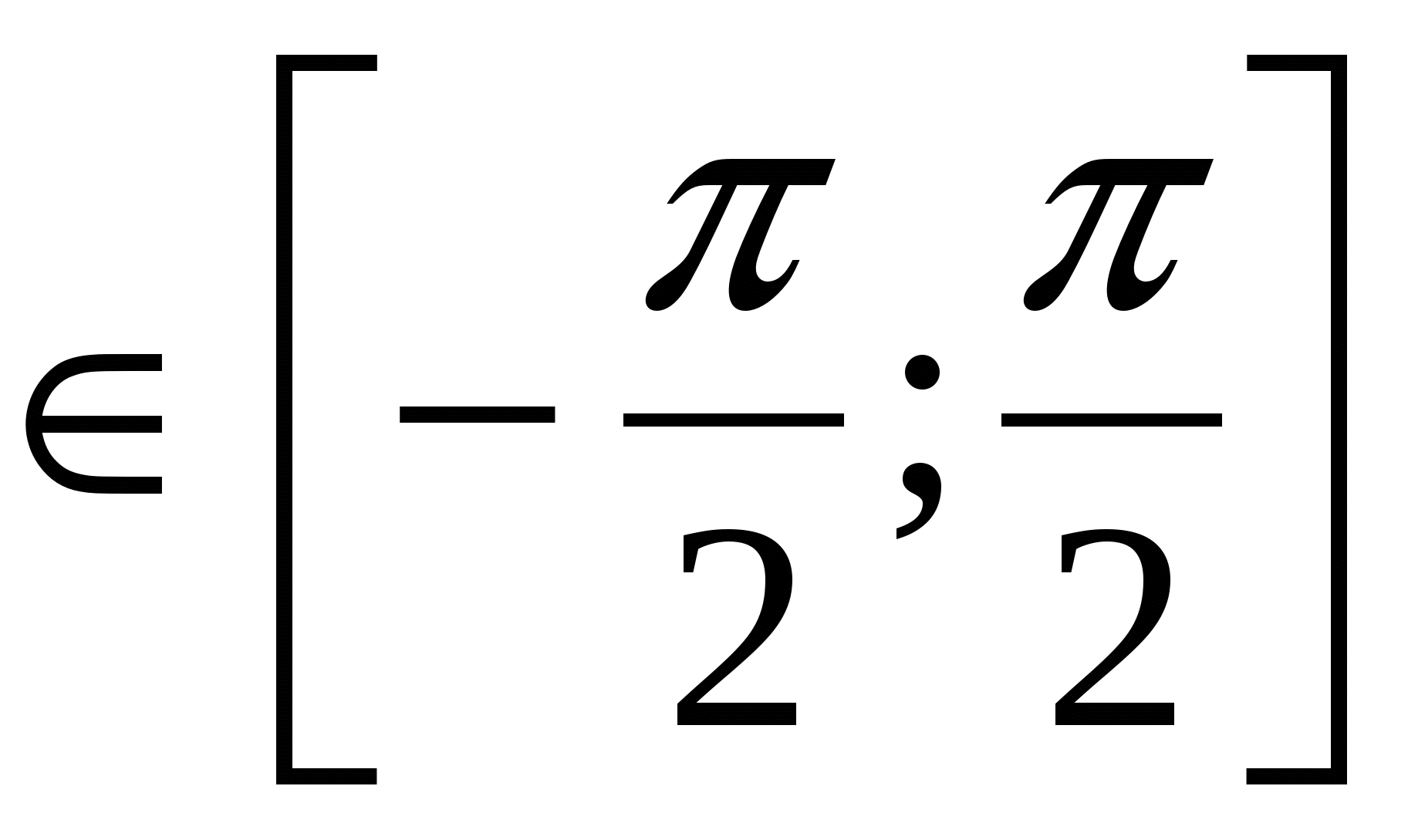
α

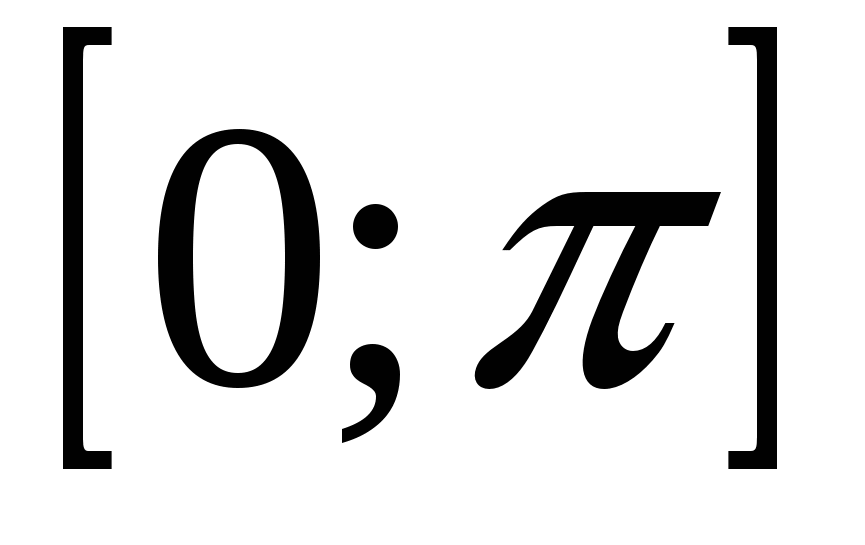
α

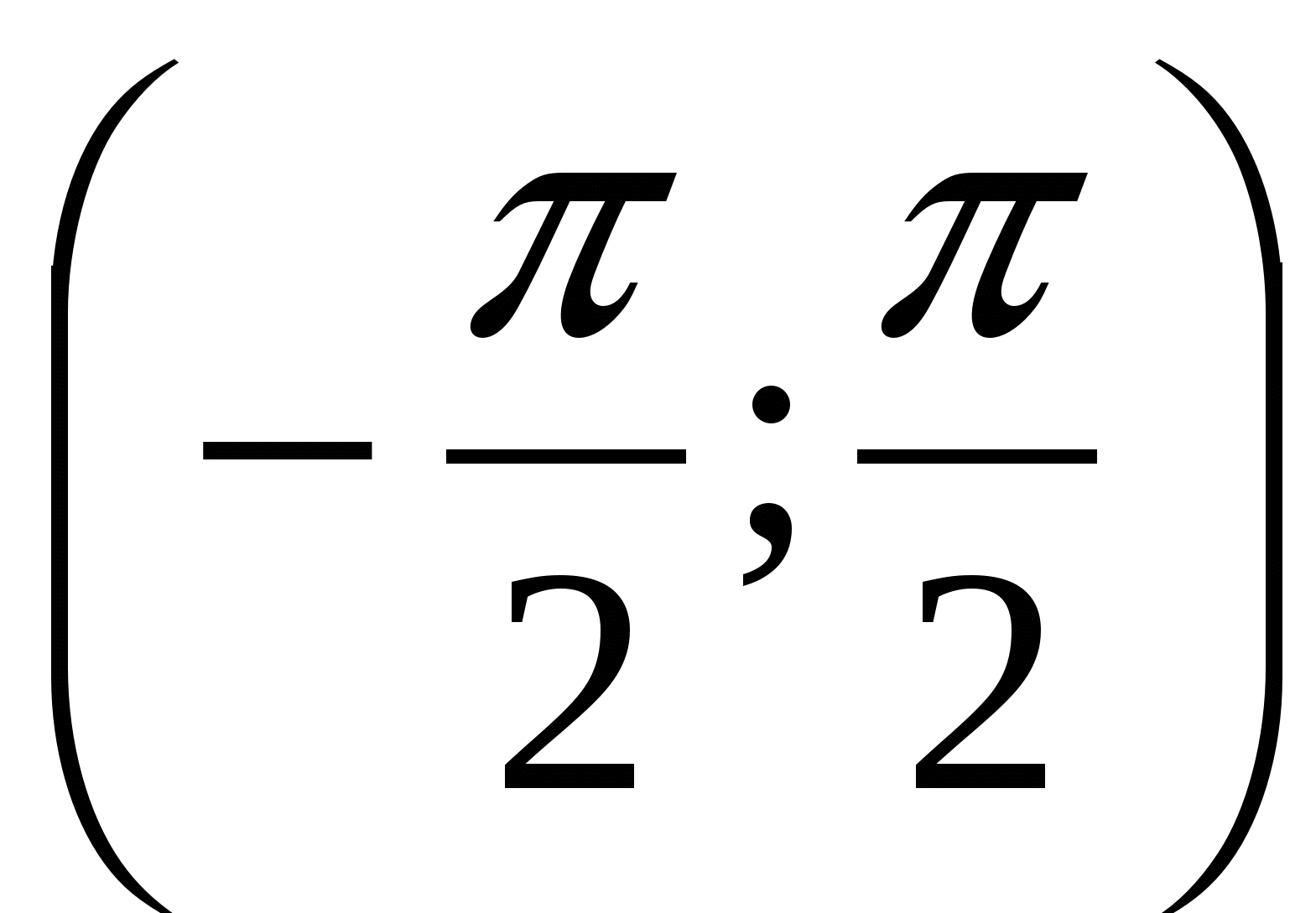
α

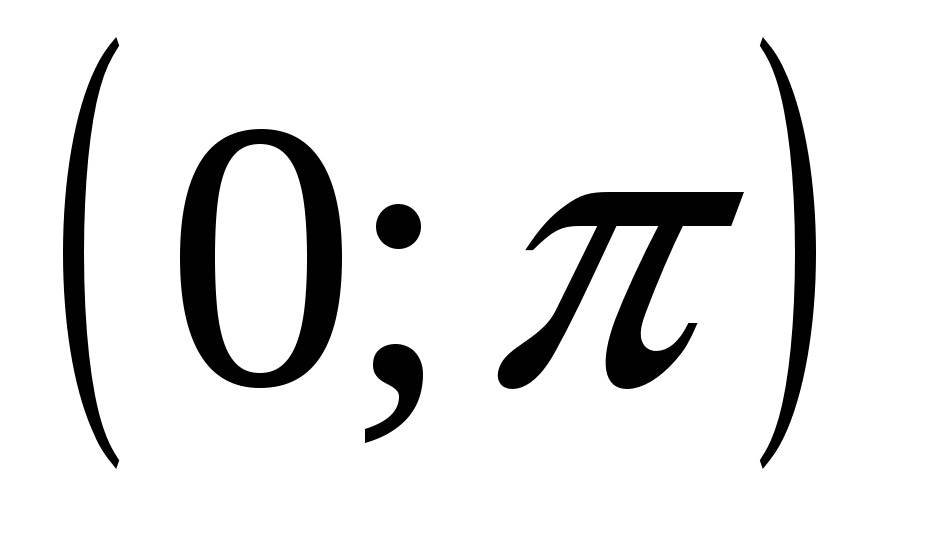
C определениями арксинуса, арккосинуса связаны следующие ошибки:

• Во-первых, часто забывают о втором условии в определениях обратных тригонометрических функций (об ограничении на множество значений) и, увидев, например равенство 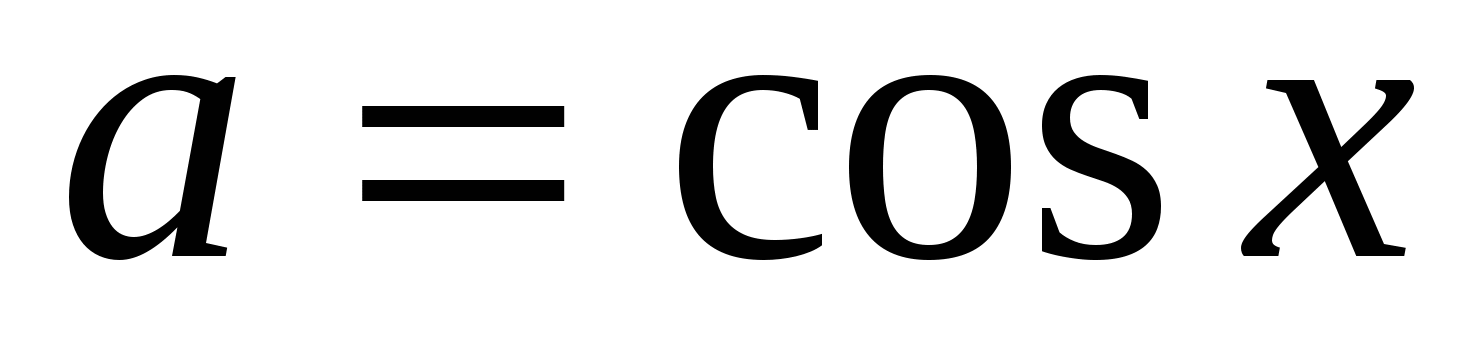сразу пишут 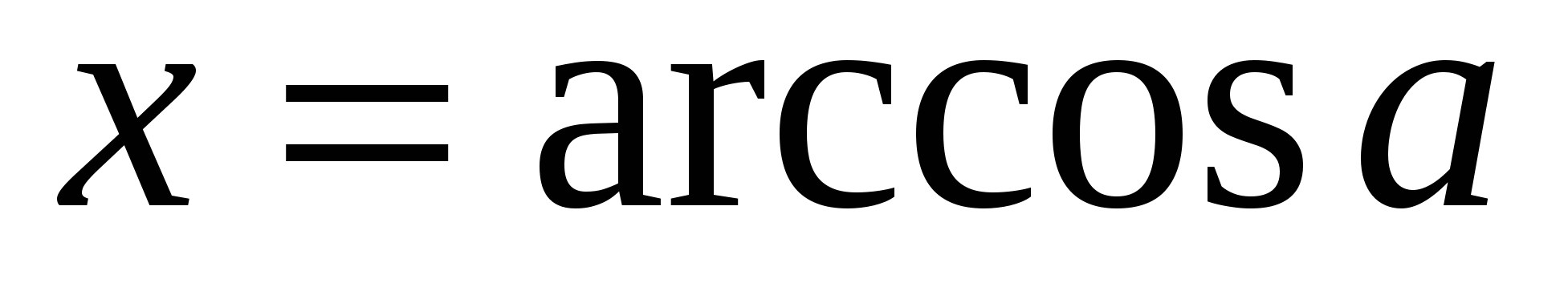. Это неверно, так как из равенства 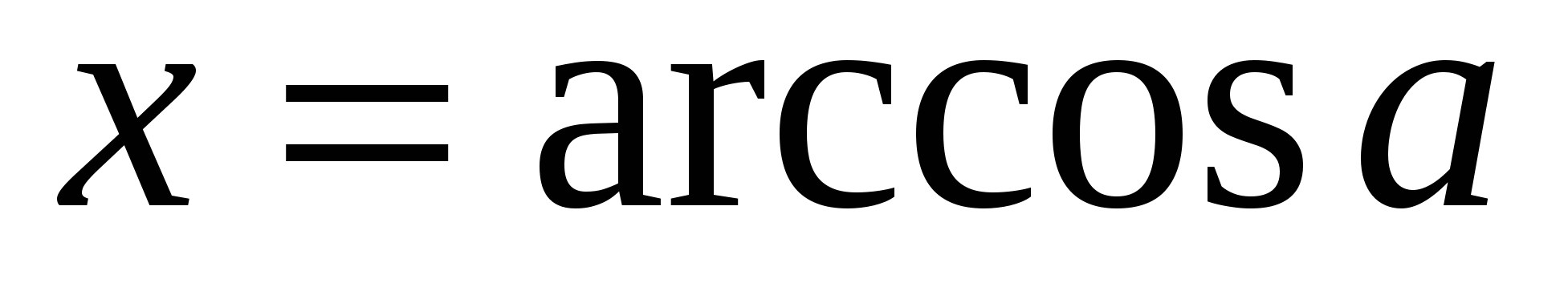не следует, что 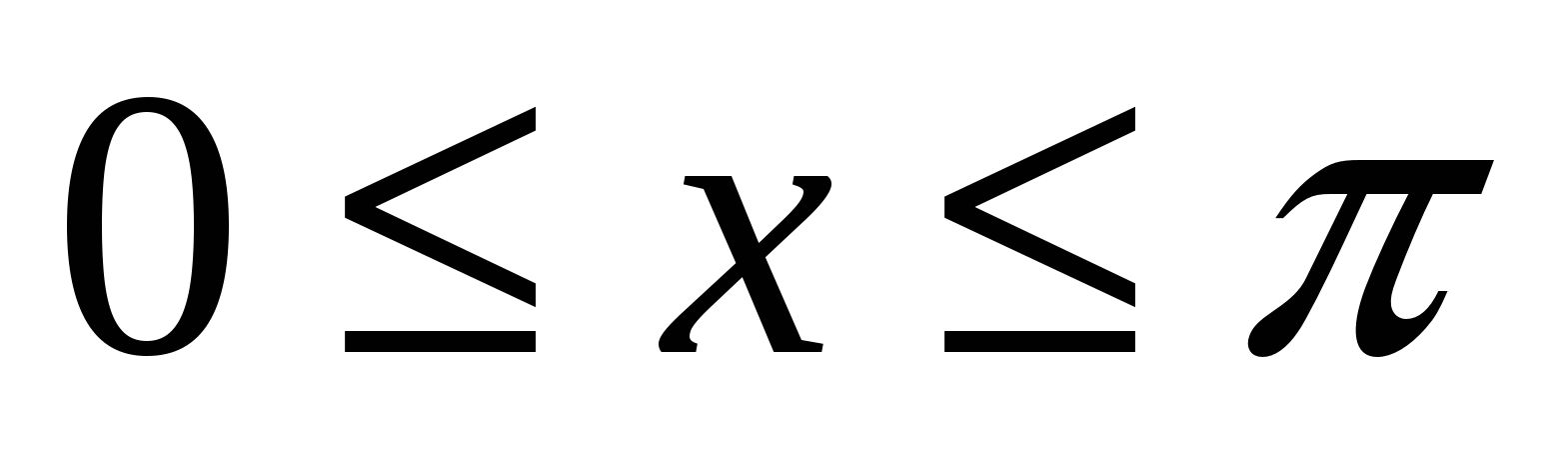; хотя первое условие определения выполнено, но ведь не ясно выполнено ли второе условие.

• Во-вторых, аналогии с тригонометрическими функциями записывают решение 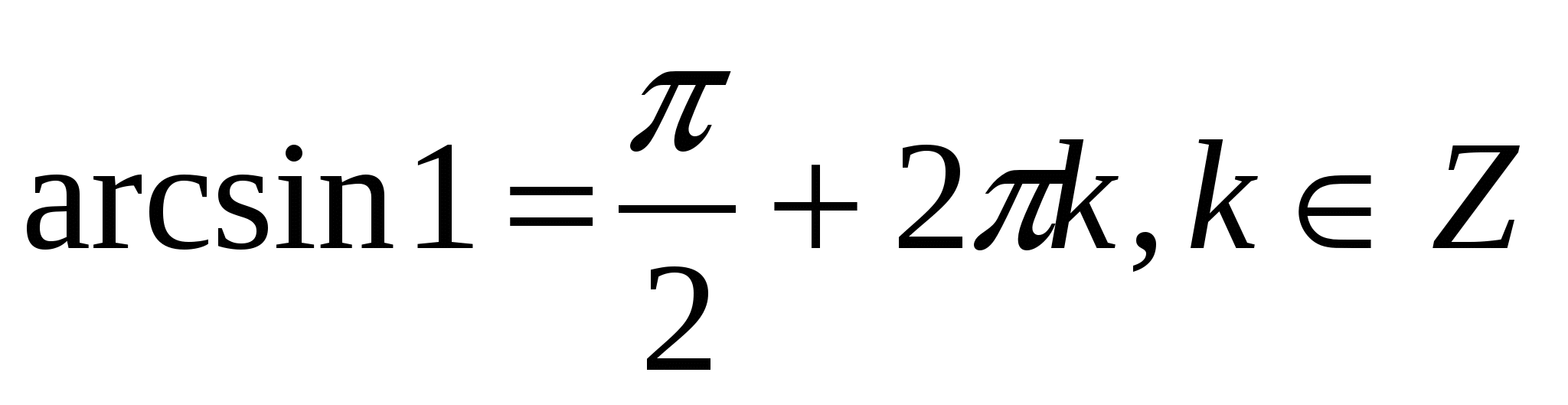, что неверно, так как множество значений arcsinx.

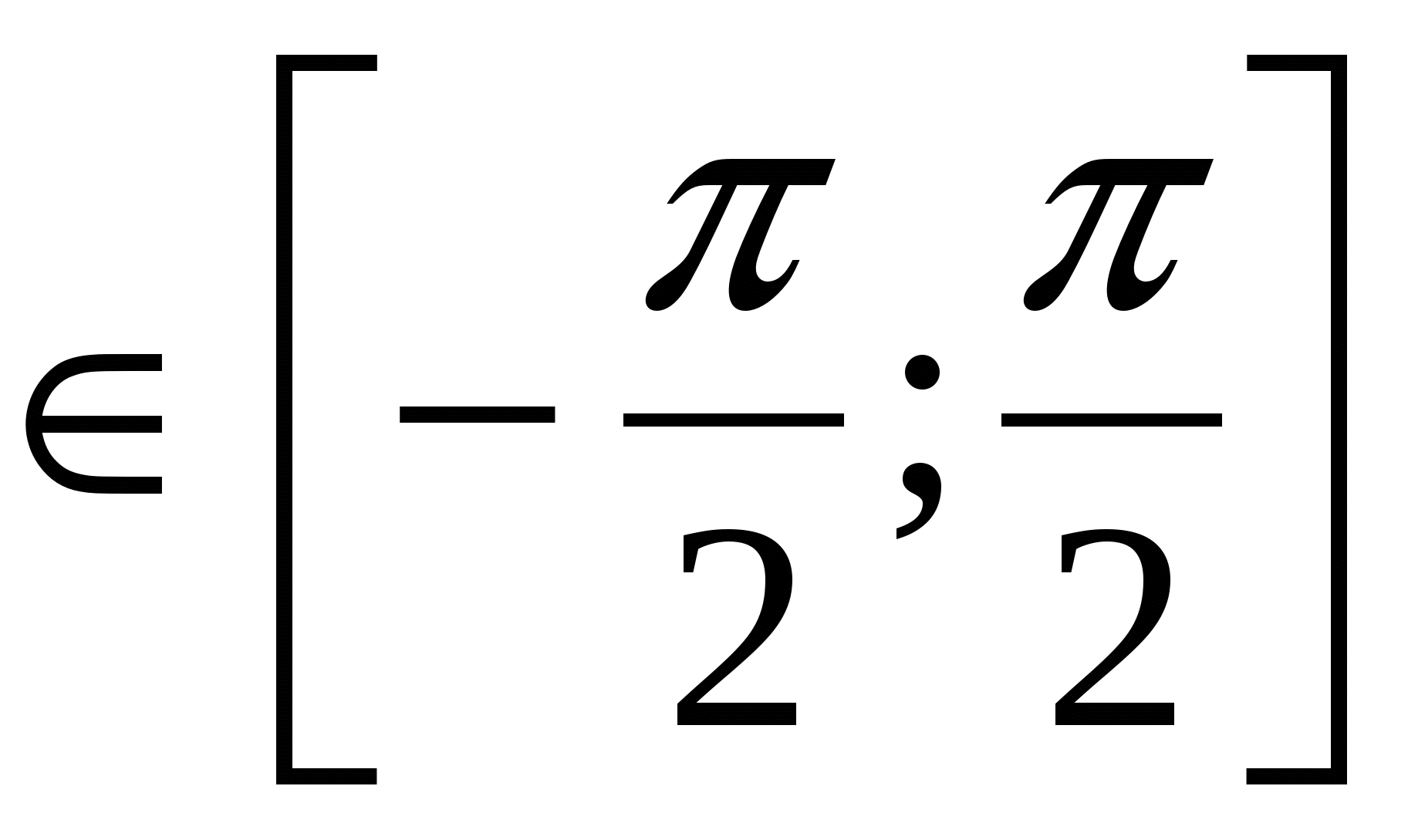• В-третьих, упускают из виду, что символы arcsinи arccosимеют смысл лишь для тех чисел , которые по модулю не превосходят единицы, т.е. для 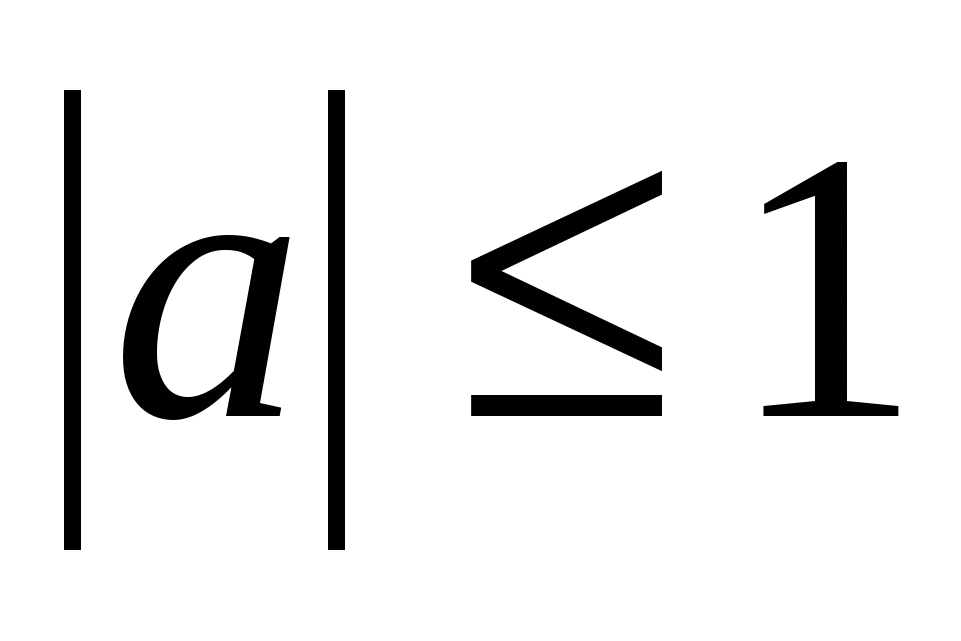и иногда употребляются, например выражения arcsin, arccos2 и другие, не имеющие смысла.

Рассмотрим два типичных примера.

Пример 1: Чему равен угол ?

Решение: По определению - это число, которое удовлетворяет двум условиям:

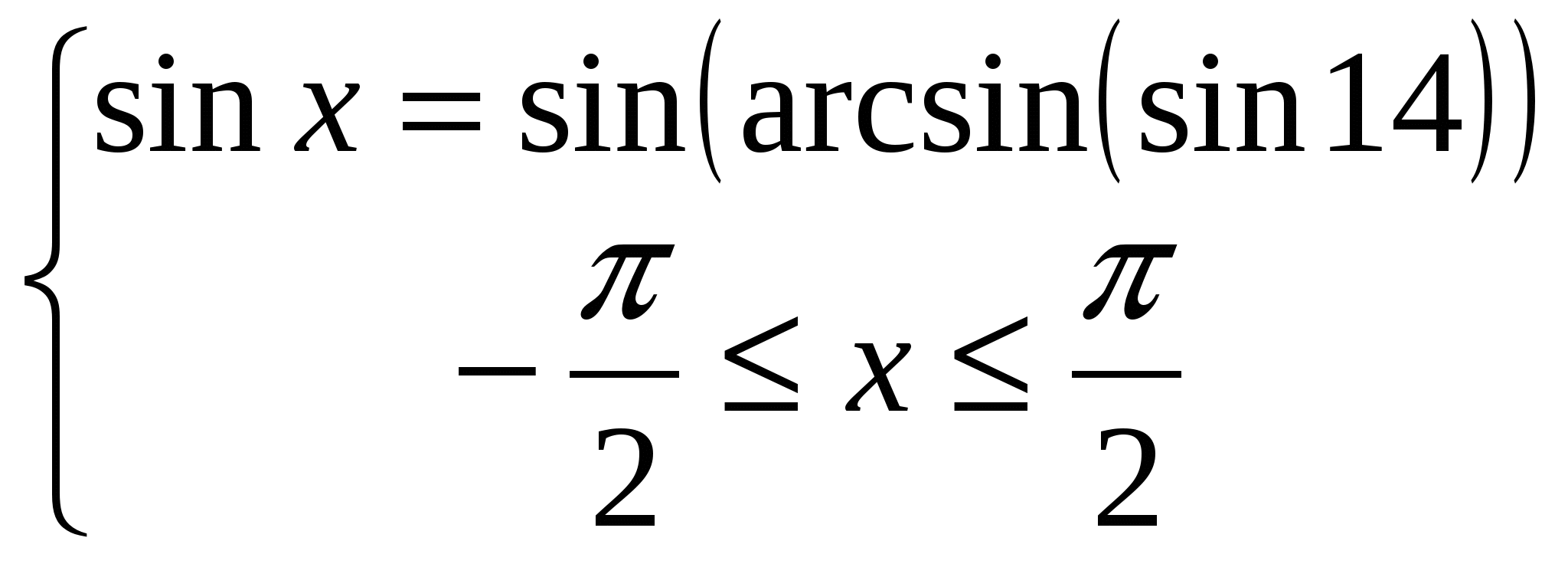, так как , то .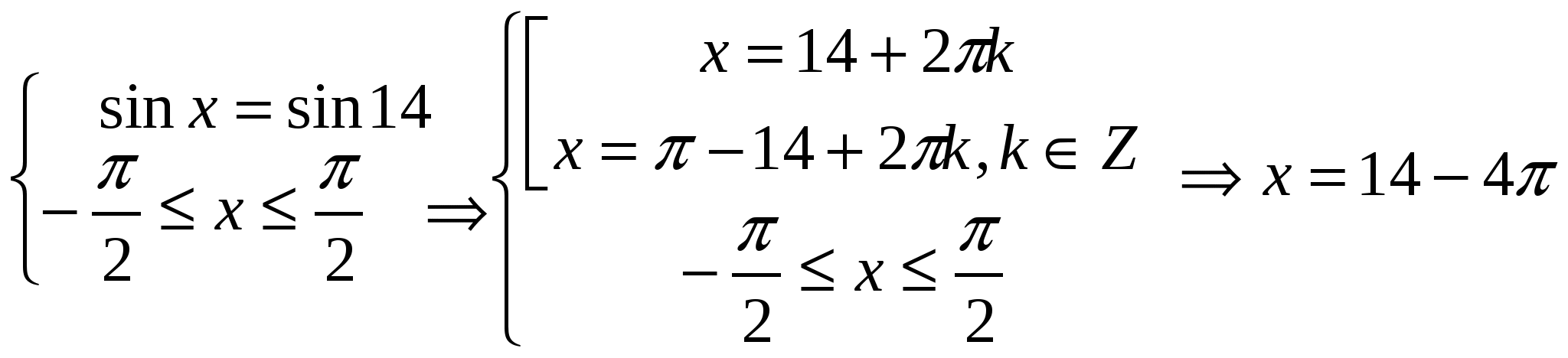

Ответ: х = 14 - 4π

Рассмотрим задание, в котором обратная тригонометрическая функция выступает в качестве аргумента тригонометрической функции.

Пример 2: Вычислить .

Решение: Соотношение между тригонометрическими функциями . Обозначим . Поскольку аргумент отрицателен, то . Во второй четверти поэтому числитель отрицателен, а знаменатель положителен. Следовательно, .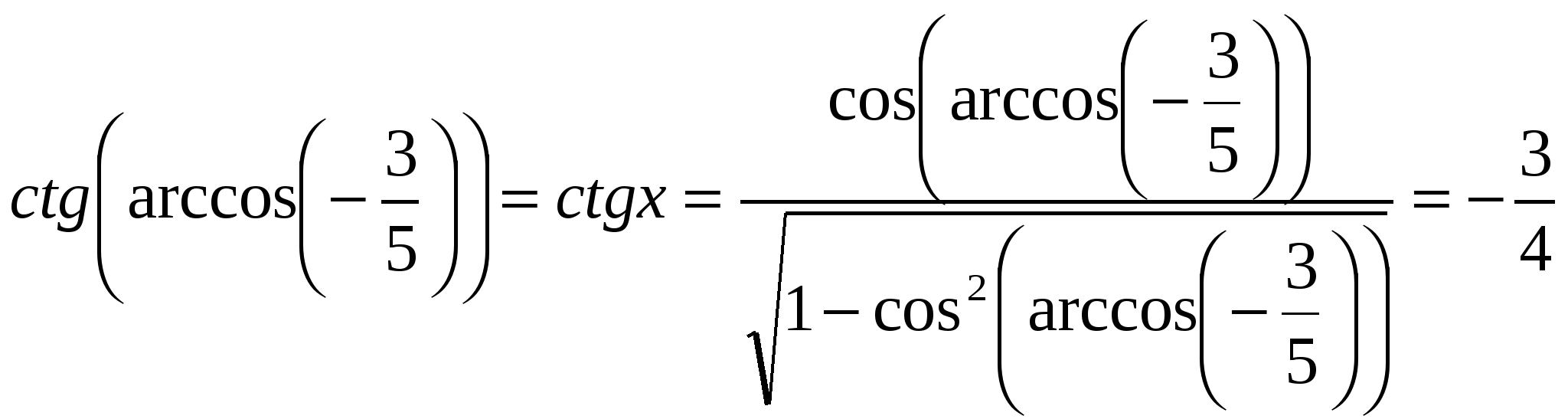

Ответ:

Никто не сомневается на сегодняшний день, что формирование компетенций ученика важно и необходимо, но возникает противоречие в том, что отсутствуют однозначные подходы к систематизации компетенций. Каждому учителю приходится самому, самостоятельно выстраивать процесс формирования компетенций.

Литература:

1. Болотов В.А., Сериков В.В. Компетентностная модель: от идеи к образовательной программе // Педагогика. - 2003,- №10, - С.8-14.

2. Гетманская А.А.,Модульный подход в формировании ключевых компетенций у учащихся // Интернет – журнал «Эйдос». – 2005. – 10 сентября. http: www.eidos.ru/journal/2005/0910-24.htm. - В надзаг: Центр дистанционного образования «Эйдос», e-mail: list@eidos.ru.

3. Ключевые компетенции и образовательные стандарты. Стенограмма обсуждения доклада А.В. Хуторского в РАО // Интернет-журнал "Эйдос". – 2002. – 23 апреля. http://www.eidos.ru/journal/2002/0423-1.htm. – В надзаг: Центр дистанционного образования "Эйдос", e-mail: [email protected].

4. Краевский В.В., Хуторской А.В. Предметное и общепредметное в образовательных стандартах // Педагогика. – 2003. – №2. – С.3 – 10.

5. Мордкович А.Г., Семёнов П.В., Алгебра и начала анализа//методическое пособие для учителя. 10 класс// профильный уровень. Москва – 2008.

6. Мордкович А.Г., Семёнов П.В., Алгебра и начала анализа//Профильный уровень. 10 класс. Учебник. Часть I- Мнемозина 2007.

7. Никольский С.М., Алгебра и начала математического анализа//11 класс. Учебник. – Просвещение. – 2008.

8. Темняткина О.В. Формирование ключевых компетенций у школьников

в образовательном процессе / О.В.Темняткина // Образование и наука.

Известия Уральского отделения Российской академии образования.-

Екатеринбург, 2006. № 4. Приложение. – 0,5 п.л.

9. Тригонометрия на экзамене по математике: учебное пособие/С.В.Королёв-М.: издательство «Экзамен», 2006.-254[2]с.(серия «Абитуриент»)

10. Фокин Ю.Г., теория и технология обучения: деятельностный подход: учеб. Пособиедля студ.в. учеб. заведений/Ю.Г. Фокин.-М.:Издательский центр «Академия», 2006.-240с.

11. Хуторской А.В. Ключевые компетенции и образовательные стандарты // Интернет-журнал "Эйдос". – 2002. – 23 апреля. http://www.eidos.ru/journal/2002/0423.htm. – В надзаг: Центр дистанционного образования "Эйдос", e-mail: [email protected].

12. Хуторской А.В. Ключевые компетенции: Технология конструирования // Народное образование. – 2003. – № 5. – С. 55 – 61.

9