Конспект урока по Математике "Геометрия окружности" 9 класс











 Урок математики в 9 классе
Урок математики в 9 классе
учителя МОУ «СОШ № 20» г. Энгельса
Милюткиной Людмилы Николаевны
и учителя математики МОУ «СОШ № 21» г. Энгельса
Лиманской Юлии Викторовны
Тема урока: «Геометрия окружности»
Тип урока: урок повторения, обобщения и систематизации знаний.
Цели урока:
1) Образовательная: повторить основные понятия и свойства окружности; закрепить умения учащихся применять теоретические знания при решении задач.
2) Развивающая: развивать математическую зоркость, логическое мышление, умение анализировать информацию, делать выводы и аргументировать их.
3) Воспитательная: воспитывать ответственность, дисциплинированность, взаимопомощь.
Формы работы: фронтальная, индивидуальная.
Оборудование: мультимедийный проектор, экран, раздаточный материал для проведения самостоятельной работы.
Предварительная подготовка:
За несколько дней ученику даётся задание создать презентацию для проведения устной разминки. Накануне урока учитель её проверяет.
Ход урока:
Этапы урока и их содержание
Время
Деятельность
учителя
учащихся
1. Организационный момент (формирование мотивации работы учащихся)
1 мин
Приветствие учащихся. Объявление темы и постановка цели урока
Записывают в тетради дату и тему урока
2. Устная разминка (актуализация знаний)
Приложение №1
10 мин
Демонстрирует презентацию ученика и проводит фронтальный опрос учащихся по теоретическим вопросам.
Повторяют основные понятия и свойства окружности
3. Закрепление и обобщение (формирование умений и навыков)
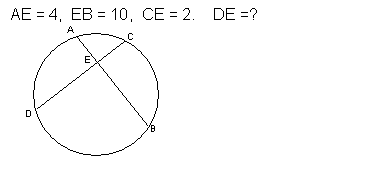
1.
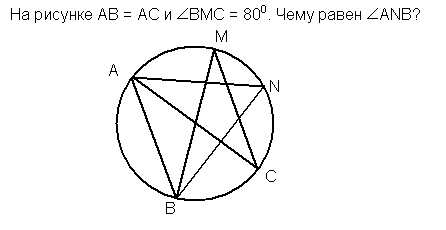
2. 
3. Из одной точки проведены две касательные к окружности. Точки касания делят окружность на две дуги, относящиеся друг к другу как 1:9. Найдите угол между касательными.
В
А 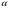
С
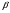
4. Докажите, что диаметр окружности, проведённый через середину хорды
(не являющейся диаметром), перпендикулярен этой хорде.
В
С
E
D
O
А
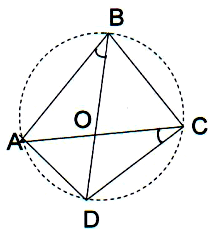
5. В выпуклом четырехугольнике АВСD диагонали АС и ВD пересекаются в точке О. 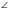 АВС = 1110 ,
АВС = 1110 , 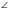 ОВС = 490 ,
ОВС = 490 , 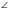 АСD = 620 . Найти углы САD и АDС.
АСD = 620 . Найти углы САD и АDС.
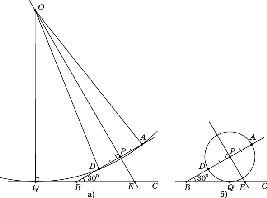
6. В ΔАВС:  А=320 и
А=320 и 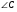 =240. Окружность с центром в точке В проходит через вершину А и сторону АС пересекает в точке М, а сторону ВС- в точке N. Найдите
=240. Окружность с центром в точке В проходит через вершину А и сторону АС пересекает в точке М, а сторону ВС- в точке N. Найдите  АNМ.
АNМ.
В
N
А M
С
7. На стороне BA угла ABC , равного 300 , взята такая точка D, что AD = 2 и
BD =1. Найдите радиус окружности, проходящей через точки A, D и касающейся прямой BC.
55 мин
10 мин
5 мин
7 мин
13 мин
20 мин
Контролирует работу учащихся
Контролирует работу учащихся
Контролирует и направляет работу учащихся
3 ученика у доски, остальные решают самостоятельно на местах, а затем проверяют:
Решение:
AE∙BE=CE∙DE  DE=
DE=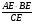 =
=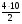 =20
=20
Ответ: DE=20
Решение:  ВАС=
ВАС= ВМС=800 т.к они опираются на одну дугу ВС. ΔВАС-равнобедренный, т.к. АВ=АС
ВМС=800 т.к они опираются на одну дугу ВС. ΔВАС-равнобедренный, т.к. АВ=АС 
 АВС=
АВС=  АСВ=
АСВ=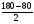 =500.
=500.
 АNB=
АNB= АСВ=500.
АСВ=500.
Ответ:  АNB=500.
АNB=500.
Решение:
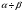 =1:9. Пусть
=1:9. Пусть 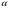 =Х0, тогда
=Х0, тогда 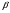 =9Х0.
=9Х0.
Получим уравнение: х+9х=360
10х=360
х=360.
Следовательно, 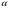 =360,
=360,
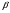 =9∙360=3240.
=9∙360=3240.
 АBС=
АBС=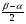 =
=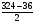 =1440.
=1440.
Ответ:  АBС=1440.
АBС=1440.
1 ученик у доски, остальные решают на местах.
Доказательство. OE – медиана треугольника COD.
Так как OC = OD, треугольник COD равнобедренный. Следовательно, OE является высотой треугольника COD. Поэтому AB 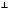 CD.
CD.
1 ученик у доски, остальные на местах.
Решение: 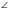 АВО = 1110 – 490 = 620.Таким образом В и С лежат по одну сторону от АD и углы АВО и АСD равны, значит точки А, В, С, D лежат на одной окружности.
АВО = 1110 – 490 = 620.Таким образом В и С лежат по одну сторону от АD и углы АВО и АСD равны, значит точки А, В, С, D лежат на одной окружности. 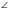 АDС и
АDС и 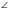 АВС вписанные, значит их сумма равна 1800 , отсюда
АВС вписанные, значит их сумма равна 1800 , отсюда 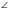 АDС = 1800 – 1110 = 690.
АDС = 1800 – 1110 = 690.
Дуга АDС равна 2220 . Значит дуга DС равна 2220 – 1240 = 980 . Угол САD вписанный и равен 490 . Ответ: 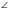 САD = 490
САD = 490 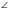 АDС = 690
АDС = 690
Решение.
 АNМ- вписан в окружность и опирается на дугу АМ. Следовательно
АNМ- вписан в окружность и опирается на дугу АМ. Следовательно  АNМ=
АNМ=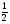
 АВМ.
АВМ.
 АBС=180-(32+24)=1240.
АBС=180-(32+24)=1240.
Рассмотрим ΔАВМ, он равнобедренный т.к. АВ=ВМ=R. Значит  А=
А= АМВ=320. Тогда
АМВ=320. Тогда  АВМ=180-32∙2=1160, а он является центральным углом, опирающимся на дугу АМ. Следовательно
АВМ=180-32∙2=1160, а он является центральным углом, опирающимся на дугу АМ. Следовательно  АNМ=116:2=580.
АNМ=116:2=580.
1 ученик у доски, остальные работают на местах.
Решение. Центр O искомой окружности принадлежит серединному
перпендикуляру к отрезку AD. Обозначим P середину отрезка AD, Q – основание перпендикуляра, опущенного из точки O на прямую BC, E – точку пересечения серединного перпендикуляра с прямой BC. Из условия касания окружности и прямой BC следует, что отрезки OA, OD и OQ
равны радиусу R окружности.
Заметим, что точка O не может лежать по ту же сторону от прямой AB, что и точка E, так как в этом случае расстояние от точки O до прямой BC меньше, чем расстояние от нее до точки A.
Из прямоугольного треугольника BPE с катетом BP = 2 и  B = 30°
B = 30°
находим, что PE = 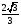 . Так как OA = R и AP =1, получаем: OP =
. Так как OA = R и AP =1, получаем: OP =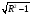 и, следовательно,
и, следовательно,
OE =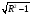 +
+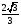 .
.
Из прямоугольного треугольника OQE, в котором  E = 60°, находим:
E = 60°, находим:
R =OQ =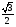 OE =
OE =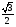
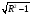 +1 .
+1 .
В результате получаем уравнение для R: 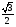
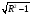 =R-1
=R-1
Возведем в квадрат обе части этого уравнения и приведем подобные члены. Получим уравнение R2– 8R + 7 = 0, решая которое находим два корня R1 = 1, R2 = 7. Если радиус равен 1, то центром окружности является точка Р .
Ответ: 1 или 7.
4. Физ. минутка
Упражнение для позвоночника стоя и для глаз сидя
1 мин
Объясняет и показывает, какие упражнения надо выполнить
Выполняют упражнения
5. Самостоятельная работа
(контроль ЗУН)
1вариант
1)Дуга радиуса 4, измеряющая центральный угол в 1200, равна длине некоторой окружности. Найдите радиус этой окружности.
2) Точка М отстоит от центра окружности на расстоянии 4. Через точку М проведена хорда, перпендикулярная диаметру окружности. Найдите длину этой хорды, если радиус окружности равен 5.
3) В окружность радиуса 5 вписан правильный треугольник, в который вписан круг, а в этот круг вписан квадрат. Найдите периметр этого квадрата.
2 вариант
1) Окружность радиуса 2 разогнута в дугу радиуса 5. Найдите получившийся центральный угол.
2) Из точки А вне окружности с центром О проведена касательная. В-точка касания. Найдите длину окружности, если АВ=10 и ОА=26.
3) Биссектриса правильного треугольника равна 21. Чему радиус круга, вписанного в этот треугольник?
20 мин
Контролирует работу учащихся
Выполняют задания на подготовленных листочках
6. Домашнее задание
(заранее написано на доске)
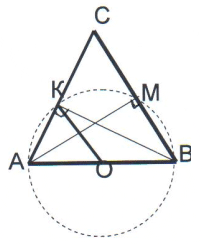
1)В треугольнике АВС проведена высота ВК. Найти длину отрезка, соединяющего точку К с серединой АВ, если АВ = 10см.
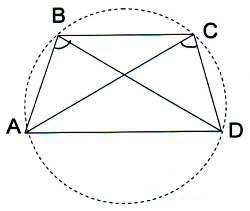
2)В трапеции АВСD с основаниями АD и ВС угол АВD равен углу АСD. Доказать, что АВСD – равнобедренная трапеция.
1 мин
Проводит инструктаж
Записывают задание в дневники
Решение:
Проведем высоту АМ, тогда углы АКВ и АМВ равны по 900 , значит точки А, К, М, В лежат на одной окружности и АВ – диаметр. Точка О – середина АС по условию
Следовательно, АО = ОВ = КО = r = 5 см.
Ответ: 5см
Решение:
Точки В и С лежат по одну сторону от АD и углы  АВD =
АВD =  АСD, то точки А, В, С,D лежат на окружности. Так как хорды ВС ║ AD , то дуга АВ равна дуге СD. Поскольку равные дуги стягивают равны хорды, то АВ = СD
АСD, то точки А, В, С,D лежат на окружности. Так как хорды ВС ║ AD , то дуга АВ равна дуге СD. Поскольку равные дуги стягивают равны хорды, то АВ = СD
7. Подведение итогов урока
2 мин
Учитель задаёт вопросы по теме: что повторили и закрепили? чему научились? Что не понятно?
Отвечают на поставленные вопросы

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ