Министерство образования Республики Мордовия

ГБОУ РМ СПО (ССУЗ) «Краснослободский промышленный техникум»

УТВЕРЖДАЮ

Зам.директора по УПР Спиркина Т.В.______

«____»____________ «___»__________2009

Методическая разработка

по математике

«Комплексные числа и действия над ними»

Согласовано

Методист

_________Ж.А.Юрченкова

«_____»_______ 20_____ г.

Рассмотрено на заседании

методической комиссии

общеобразовательных дисциплин

Председатель м/к__________В.А.Новиков

Разработала: преподаватель Кудашкина И.П.

2013 г.

Содержание

Аннотация…………………………………………………………………………4

Введение ………………………………………………………………………......5

Основная часть …………………………………………………………………...6

Заключение ……………………………………………………………………...14

Список литературы и другие источники ……………………………………..15

Приложение А…………………………………………………………………...16

Аннотация

"Помимо и даже против воли того или другого математика, мнимые числа снова и снова появляются на выкладках, и лишь постепенно, по мере того как обнаруживается польза от их употребления, они получают более и более широкое распространение”

Ф. Клейн.

В настоящее время трудно указать область физики, механики, технических дисциплин, где не применялись бы комплексные, числа.

Комплексные числа [3, 205], следует отметить, имеют большое познавательное и практическое значение. Их изучение в курсе математики стало весьма актуальным.

Тема "Комплексные числа" - одна из ведущих прикладных тем курса математики для техникумов, ее содержание углубляется в общетехнических и специальных предметах, таких, как "Электротехника".

После изучения темы «Комплексные числа учащиеся должны:

Знать: алгебраическую, геометрическую и тригонометрическую формы комплексного числа.

Уметь: производить над комплексными числами операции сложения, умножения, вычитания, деления, возведения в степень, извлечение корня из комплексного числа; переводить комплексные числа из алгебраической формы в геометрическую и тригонометрическую; пользоваться геометрической интерпретацией комплексных чисел; в простейших случаях находить комплексные корни уравнений с действительными коэффициентами.

Введение

Комплексные числа, как, впрочем, и отрицательные, возникли из внутренней потребности самой математики, конкретнее – из практики и теории решения алгебраических уравнений. С комплексными числами впервые математики встретились при решении квадратных уравнений. Вплоть до 16 века математики всего мира, не находя приемлемого толкования для комплексных корней, возникавших при решении квадратных уравнений, объявляли их ложными и не принимали во внимание. И только в начале 19 века, когда уже была выяснена роль комплексных чисел в различных областях математики, была разработана очень простая и естественная их геометрическая интерпретация, позволившая уяснить геометрический смысл операций над комплексными числами. Тем самым был положен конец сомнениям в законном и полезном применении комплексного числа.

Долгое время данная тема не изучалась на уроках математики. Ознакомление и изучение комплексных чисел учащимися позволит им углубить познания во многих разделах математики, вооружит их дополнительным инструментом для решения различных задач.

Тема урока: Комплексные числа и действия над ними

Мы... никогда не стали бы разумными, если бы исключили число из человеческой природы.

Платон

Цели урока:

Образовательные:

1. Обобщить и систематизировать знания, умения и навыки учащихся по теме «Комплексные числа»

Развивающие:

1. Развивать мышление в процессе выполнения практических заданий.

2. Развивать умение анализировать, сравнивать, обобщать, устанавливать причинно-следственные связи, классифицировать.

Воспитывающие:

1. Воспитывать культуру записей в тетради.

2. Сформировать навыки самостоятельной деятельности;

Форма урока: урок-практикум.

Тип урока: Урок применения знаний, умений и навыков

Формы организации труда: индивидуальная, коллективная

Методы: словесные, практические, проблемно-поисковые

Учебная цель: Овладение навыками выполнения действий над комплексными числами

Оборудование урока: компьютер, мультимедийная установка, презентация «История комплексных чисел», тест «Комплексные числа»

Структура урока.

1. Организационный момент.

2. Этап «Вызов»

3. Этап «Осмысление»

4. Домашнее задание.

5. Подведение итогов урока.

Ход урока:

I. Организационный момент.

Рапорт дежурного. Сообщение темы и целей урока.

II. Этап «Вызов»

Расширение множества вещественных чисел состоит в том, что к действительным числам присоединяются новые числа (мнимые). Введение этих чисел связано с невозможностью во множестве действительных чисел извлечения корня из отрицательного числа.

2.1 Кроссворд

Давайте, посредством кроссворда вспомним известные нам множества чисел.

¹в

ы

ч

и

т

а

н

и

е

²р

а

ц

и

о

н

а

л

ь

н

ы

е

³к

о

м

п

л

е

к

с

н

ы

е

⁴ц

е

л

ы

е

⁵н

а

т

у

р

а

л

ь

н

ы

е

1. Одно из арифметических действий над числами.

2. Числа, представленные в виде дроби 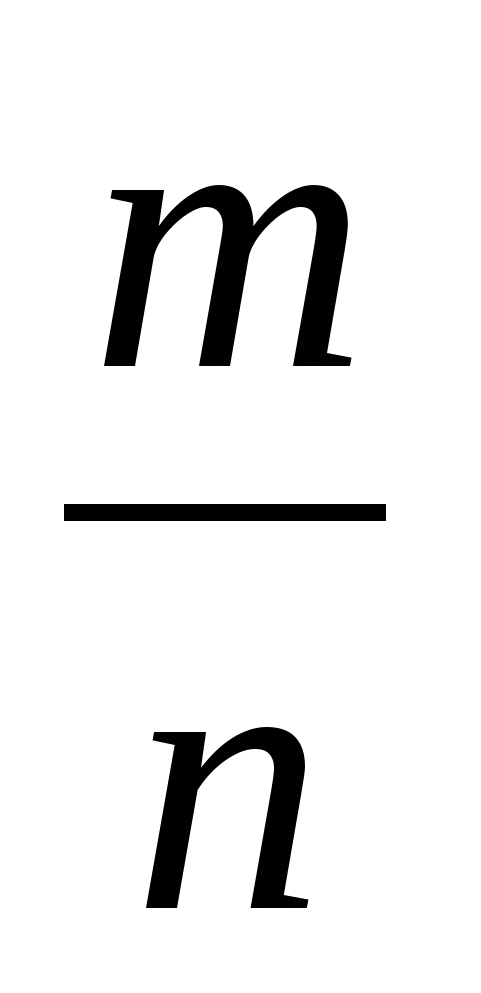, где m-целое число, а n-натуральное число

3. Числа вида х + iy, где х и у — действительные числа, а i — так называемая мнимая единица

4. Множество этих чисел состоит из трех частей – натуральные числа, отрицательные целые числа (противоположные натуральным числам) и число 0 (нуль).

5. Числа, получаемые при естественном счёте предметов, а вернее при их нумерации («первый», «второй», «третий»...).

2.3. Формульный тест

№1. Комплексными числами называются числа вида x+yi,где i- мнимая единица , а x и y -

1. целые числа

2. натуральные числа

3. действительные числа

4. рациональные числа

№2. Модуль комплексного числа z=x+yi равен

1)

2)

3)

4)

№3. Какое число является комплексно-сопряженным числу z=x+yi

1. z=-x+yi

2. z=x-yi

3. z=-x-yi

4. z=x+yi

№4. Сумма двух комплексных чисел z₁=a+bi и z₂=c+di равна

1. (a + bi ) + (c + di ) = (a + c) + (b + d)i

2. (a + bi ) + (c + di ) = (a + c) - (b + d)i

3. (a + bi ) + (c + di ) = (a - c) + (b - d)i

4. (a + bi ) + (c + di ) = (a + d) + (b + c)i

№5. Произведение двух комплексных чисел z₁=a+bi и z₂=c+di равно

1. (a + bi ) * (c + di ) = (ac – bd) - (bc + ad)i

2. (a + bi ) * (c + di ) = (ac – bd) + (bc + ad)i

3. (a + bi ) * (c + di ) = (ac + bd) + (bc + ad)i

4. (a + bi ) * (c + di ) = (ac + bd) - (bc + ad)i

№6. Тригонометрическая форма комплексного числа z=a+bi имеет вид

1)

2)

3)

4)

№7. Разность двух комплексных чисел z₁=a+bi и z₂=c+di равна

1. (a + bi ) - (c + di ) = (a + c) - (b + d)i

2. (a + bi ) - (c + di ) = (a - c) + (b - d)i

3. (a + bi ) - (c + di ) = (a - c) + (b + d)i

4. (a + bi ) - (c + di ) = (a - d) + (b - c)i

№8. Действительная и мнимая части числа z=3-2i равны

1. Re z= 3 Im z= -2

2. Re z= 3 Im z= 2

3. Re z= 2 Im z= -3

4. Re z= -2 Im z= 3

III. Этап осмысления «Творческая лаборатория»

Многие учёные на протяжении веков внесли свой вклад в изучение комплексных чисел. Осуществит экскурс в историю комплексных чисел, помогут задания.

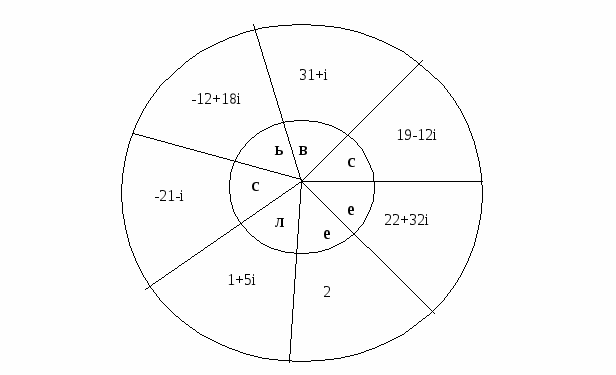
Задание 1. «Магическая таблица» С помощью таблицы узнайте имя итальянского алгебраиста, предложившего в 1545 ввод числа новой природы. ( Джироламо Кардано) Для этого необходимо прочесть буквы, образованные пересечением номера столбца и номера строки.

0 1+3i 2+2i 3+i 2+0i 2+i 1 3+3i 3i

3 2+3i 2i 3+2i 1+i i 1+2i

Действительная часть числа

Мнимая часть числа

0

1

2

3

0

д

а

о

к

1

н

а

л

р

2

р

о

и

д

3

o

ж

а

м

На рубеже 17-18 веков была построена общая теория корней n-й степени сначала из отрицательных, а впоследствии и из любых комплексных чисел.

Задание 2. «Морской бой». Узнайте имя ученого, предложившего символ для обозначения мнимой единицы (Эйлер).

Для этого нужно прочесть числа на координатной плоскости.

л

л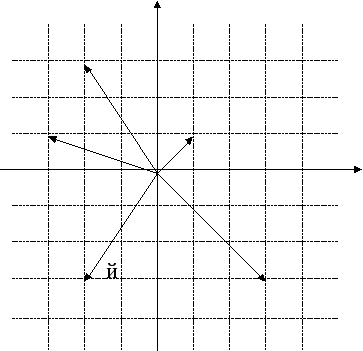

y= Im z

л

е

р

э

x=Re z

э

(3;-3) (-2;-3) (-2;3) (1;1) (-3;1)

Задание 3. Произведите арифметические действия над комплексными числами и узнайте, имя французского математика, который в конце 18 века смог сказать, что математический анализ уже не затрудняют мнимые величины (Лагранж)

1) (3 + 5i) + (7 – 2i).
2) (6 + 2i) + (5 + 3i).
3) (– 2 + 3i) + (7 – 2i).
4) (5 – 4i) + (6 + 2i).
5) (3 – 2i) + (5 + i).
6) (4 + 2i) + (– 3 + 2i)
7) (– 5 + 2i) + (5 + 2i).

Л=10-2i ж=4i а=8-i г=5+i р=11-2i н=1+4i а=11+5i Задание 4. Произведите арифметические действия над комплексными числами [3, 206-207] и узнайте, имя ученого, предложившего изображать комплексное число точкой на координатной плоскости. (Датчанин Вессель, француз Арган и немец Гаусс)

1. ___ (2 + 3i)(5 – 7i).=
2. ___(6 + 4i)(5 + 2i)=
3. ___(3 – 2i)(7 – i).=
4. ___ (– 2 + 3i)(3 + 5i)=
5. ___(1 –i)(1 + i)=
6.___ (3 + 2i)(1 + i)=
7. ___(6 + 4i)3i=

Самостоятельная работа .

Записать в тригонометрической форме комплексное число.

работа по вариантам:

(2 ученика у доски для проверки решения)

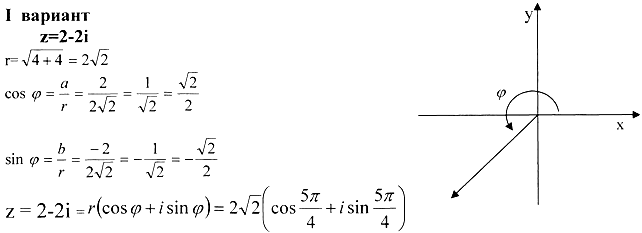
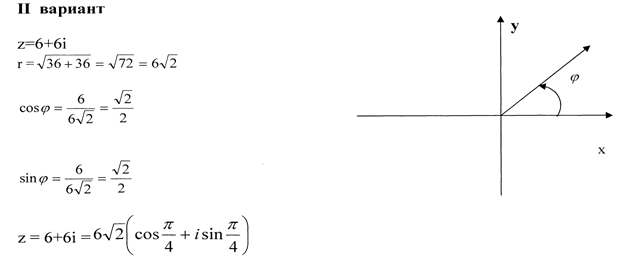
Записать полученный результат в показательной форме

IV.Домашнее задание: Подготовить сообщения о истории комплексных чисел

V. Подведение итогов урока.

Заключение

Тема “Комплексные числа” развивает и углубляет заложенные в основном курсе математики представления о многочленах и числах, в известном смысле завершая путь развития понятия числа в средней школе.

Приступая к работе над методической разработкой по теме» Комплексные числа», ставила следующие цели повышение математической культуры учащихся; углубление представлений о понятии числа; дальнейшее развитие представлений о единстве математики как науки. Цели урока достигнуты.

Следует отметить важное прикладное значение данной темы ввиду обилия приложения изучаемых понятий как внутри самой математики, так и в различных областях физики, техники и других наук, использующих математический аппарат.

Список использованной литературы

1.Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., Просвещение, 2007.

2.Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М.Просвещение, 2009.

3.Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 11 кл. – М.Просвещение , 2010.

4.Задачи по алгебре и началам анализа: Пособие для учащихся 10–11 кл. общеобразоват. учреждений /С.М. Саакян, А.М. Гольдман, Д.В. Денисов. – М.: Просвещение, 2003.

5.Научно-теоретический и методический журнал «Математика в школе»

Приложение А

Презентация «История комплексных чисел», 24 слайда

Приложение В

Электронный тест «Комплексные числа»