Конспект урока по математике "НЕКОТОРЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ" 8 класс
ФИО: Михайлова Елена Егоровна
Образовательное учреждение: МБОУ г. Магадана "СОШ с УИМ № 15"
Должность: учитель математики
8 класс.
ТЕМА: «НЕКОТОРЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ»
ЦЕЛЬ УРОКА:
Учебная: Повторить определение квадратных уравнений.
Повторить решение уравнений с помощью формул дискриминанта и корней квадратного уравнения.
Повторить привила необходимые при решении квадратных уравнений (действия с рациональными числами, порядок действий и другие)
Учащиеся должны открыть другие способы решения квадратных уравнений (через свойство коэффициентов квадратного уравнения и теорему обратную теореме Виета)
Развивающая: Развивать в учащихся умение анализировать, сравнивать, выделять
главное, обобщать и систематизировать. Продолжить работу над развитием речи учеников.
Воспитательная: Учащиеся привлекаются к активной познавательной деятельности, им
предлагается самостоятельно решать проблемы, что учит настойчивости в достижении цели, умению отстаивать свои взгляды при этом слушать и слышать оппонента.
Форма проведения урока: Групповая работа в сочетании с индивидуальной работой в нутрии группы.
Тип урока: Приобретение новых знаний, в основе которого лежит самостоятельная умственная деятельность учащихся.
ХОД УРОКА.
1 ЭТАП
2 мин.
2 ЭТАП.
3 мин.
3 ЭТАП.
2 мин.
4 ЭТАП.
2мин.
5 ЭТАП.
5мин.
6 ЭТАП.
4мин.
7 ЭТАП.
4 мин.
8 ЭТАП.
2 мин.
9 ЭТАП.
3мин.
10 ЭТАП.
2мин.
11 ЭТАП.
Приветствие. Сообщение целей урока.
Угнетает меня повседневность сует,
И обиды в душе оставляют свой след.
Но с трепетом, с радостью в класс я вхожу
Наконец-то! Вот здесь только я и дышу.
Здесь дают мне энергию 12 пар глаз,
Я могу поделиться, и дать про запас.
Вот метнулся навстречу улыбок салют.
«Ты мгновенье прекрасно» - себе говорю
ты мгновенье замри, только это не жизнь,
отомри! И начнем. Торопись! Торопись!
Я предлагаю вам торопится пробежать по межзвездному пространству темы: «Решение квадратных уравнений» и открыть для себя звезду «Некоторых способов решения квадратных уравнений»
Мы повторим правила решения квадратных уравнений с использованием формул дискриминанта и корней квадратного уравнения.
Работать вы будете на листах выданных мною индивидуально и в группах. И оценивать ваши знания я буду по работе на этих карточках и по вашим устным ответам.
При работе в группах прислушайтесь к высказыванию
Бернарда Шоу (английский писатель (1856-1950)) он говорил:
Если у вас есть яблоко и у меня есть яблоко и если мы обмениваемся этими яблоками, то у вас и у меня остается по одному яблоку. А если у вас есть идея и у меня есть идея и мы обмениваемся идеями, то у каждого из нас будет по две идеи.
Повторить определение квадратного уравнения.
ЗАДАНИЕ НА ДОСКЕ:
Дайте определение квадратного уравнения стандартного вида.
Из приведенных уравнений выберете те, которые являются квадратными уравнениями.
3х – 5 = 0 2х2 – 5х + 3 = 0 4х2 + 5 = 0 7х2 – 6х = 1
5х - 2х2 + 3 = 0 4х2 – 7х + 3 = 4х2 х3 + 2х = 0
Назовите коэффициенты квадратного уравнения.
5х - 2х2 + 3 = 0
Деяние есть
живое единство
теории и практики
Деяние есть живое единство теории и практики. Аристотель (древнегреческий философ (384-322гг. до н.э.)
Найдите закономерность и продолжите ряд:
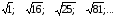 ОТВЕТ: 1; 4; 5; 9; 13; 21 …
ОТВЕТ: 1; 4; 5; 9; 13; 21 …
КАРТОЧКА 1. ЗАДАНИЕ 1. Найдите ошибку в решении.
Учащиеся работают самостоятельно в группе.
Проверка с мультимедийным пректором.
КАРТОЧКА 1. ЗАДАНИЕ 2.
Учащиеся работают самостоятельно в группе, каждый на своем листе.
ОБСУЖДЕНИЕ ПОЛУЧИВЩИХСЯ РЕЗУЛЬТАТОВ.
ВЫВОД ЗАКОНОМЕРНОСТИ.
ЗАПОЛНЕНИЕ ЧАСТИ БЛОК – СХЕМЫ В ГРУППЕ.
а) Один представитель от группы заполняет блок – схему на доске.
б) рассказ учителя об истории развития квадратных уравнений
Неполные квадратные уравнения и частные виды полных квадратных уравнений (х2 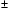 х = а) умели решать вавилоняне (около 2 тыс. лет до н.э.) об этом свидетельствуют найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Приемы решения уравнений без обращения к георетрии дает Диофант Александрийский (III в.) В дошедших до нас 6 из 13 книг «Арифметика» содержаться задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получить решение уравнения вида ах = b или ах2 =b. Способ решения полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. В VII веке индийский ученый Брахмагупта дал способ решения квадратных уравнений при а> 0. Хорезмский математик аль-Хорезми разъясняет приемы решения всех видов квадратных уравнений, но лишь для положительных коэффициентов и положительных корней. Общее правило решения квадратных уравнений, приведенных к виду х2 + bх = с, было сформулировано немецким математиком М. Штифелем (1487 – 1567).
х = а) умели решать вавилоняне (около 2 тыс. лет до н.э.) об этом свидетельствуют найденные клинописные тексты задач с решениями (в виде рецептов). Некоторые виды квадратных уравнений, сводя их решение к геометрическим построениям, могли решать древнегреческие математики. Приемы решения уравнений без обращения к георетрии дает Диофант Александрийский (III в.) В дошедших до нас 6 из 13 книг «Арифметика» содержаться задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получить решение уравнения вида ах = b или ах2 =b. Способ решения полных квадратных уравнений Диофант изложил в книгах «Арифметика», которые не сохранились. В VII веке индийский ученый Брахмагупта дал способ решения квадратных уравнений при а> 0. Хорезмский математик аль-Хорезми разъясняет приемы решения всех видов квадратных уравнений, но лишь для положительных коэффициентов и положительных корней. Общее правило решения квадратных уравнений, приведенных к виду х2 + bх = с, было сформулировано немецким математиком М. Штифелем (1487 – 1567).
Ученики озвучивают ВЫВОДЫ у доски.
ЗАПОЛНЕНИЕ БЛОК – СХЕМЫ КАЖДЫМ УЧЕНИКОМ.
ДОМАШНЕЕ ЗАДАНИЕ.
ПРИМЕНЕНИЕ НОВЫХ СВОЙСТВ К РЕШЕНИЮ ПРИДУМАННЫХ УРАВНЕНИЙ.
Карточка 3
дополнительно
Придумать уравнения одно на свое правило другое на правило из другой группы. Решить 1-2 уравнения.
ВЫВОДЫ.
КАРТОЧКА № 1.
ГРУППА № 1. Ученик:_____________________________________
Время.
2 мин.
2 мин.
3 мин.
2мин.
4 мин.
Выполняемая работа.
Задание 1.
Найдите ошибку в решении.
6х2 – 13х + 2 = 0
D= b2 - 4ac; D = (-13)2 – 4 6 2 = 169 – 48 = 121>0, 2 корня
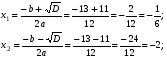
Ответ: х1 =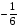 , х2= - 2.
, х2= - 2.
Задание 2.
Обсуждение с учителем результатов пункта 1.
Задание 3.
Решите уравнение, используя формулы дискриминанта и корней квадратного уравнения.
4х2 – 7х + 3 = 0
______________________________________
_______________________________________
_______________________________________
Ответ: ___________________
По окончании решения найди на парте звездочку со своим ответом, если звездочки с твоим ответом нет, то твое решение неверное, найди ошибку.
Задание 4.
Выпиши значения коэффициентов квадратного уравнения из задания 3.
а =_________b= с =________
проверь, выполняется ли для этих коэффициентов равенство:
а + b + с = 0:_________________________________________
Задание 5.
Вместе с товарищами по группе заполни на КАРТОЧКЕ 2 колонку, обозначенную ГРУППА 1 и 3.
ГРУППА 1 и 2
ГРУППА 3 И 4
Домашнее задание.
ВИД
КОРНИ
ВИД
КОРНИ
ВИД
КОРНИ
х1 + х2
х1 х2
3х2 – 2х – 1 = 0
2х2 – 5х + 3 = 0
4х2 – 9х + 5 = 0
2х2 + 3х – 5 = 0
7х2 – 6х – 1 = 0
4х2 – 7х + 3 = 0
6х2 + 5х - 1 = 0
3х2 + 5х + 2 = 0
7х2 + 9х + 2 = 0
5х2 + 2х - 3 = 0
3х2 + 8х + 5 = 0
7х2 + 8х + 1 = 0
х2 – 3х – 10 = 0
х2 + 7х + 10 = 0
х2 + 6х + 5 = 0
х2 – 9х + 20 = 0
х2 – 2х – 15 = 0
х2 + 2х – 15 = 0
ГРУППА 1 и 3 КАРТОЧКА 2 ГРУППА 2 и 4
ВИД
Значение
а + b + c равно
КОРНИ
а
b
c
ВИД
Значение
а + b + c равно
КОРНИ
а
b
с
3х2 – 2х – 1 = 0
2х2 – 5х + 3 = 0
4х2 – 9х + 5 = 0
6х2 + 5х - 1 = 0
3х2 + 5х + 2 = 0
7х2 + 9х + 2 = 0
Обсудите в группе результаты данной колонки. Найдите закономерность между корнями уравнения и его коэффициентами. Заполните пропуски в выводе.
Обсудите в группе результаты данной колонки. Найдите закономерность между корнями уравнения и его коэффициентами. Заполните пропуски в выводе.
ВЫВОД: Если для коэффициентов квадратного уравнения выполняется условие __________________ , то один из корней всегда равен_____ , а второй можно выразить через коэффициенты квадратного уравнения и получится
формула
__________
ВЫВОД: Если для коэффициентов квадратного уравнения выполняется условие __________________ , то один из корней всегда равен_____ , а второй можно выразить через коэффициенты квадратного уравнения и получится
формула
___________
КАРТОЧКА 3
Решите уравнения из таблицы, используя формулы дискриминанта и корней квадратного уравнения.
Заполните таблицу.
Домашнее задание.
ВИД
КОРНИ
Значение х1 + х2
равно
Значение х1 х2
равно
b
с
х2 – 3х – 10 = 0
х2 + 7х + 10 = 0
х2 + 6х + 5 = 0
. Найдите закономерность между значениями
х1 + х2, х1 х2 и коэффициентами квадратных уравнений. Заполните пропуски в выводе
ВЫВОД: Если в квадратном уравнении первый коэффициент а = ___ ,
D 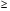 0 и то для корней этого уравнения выполняется условие
0 и то для корней этого уравнения выполняется условие
х1 + х2_= ___ , х1 х2 =______________.
Узнай, как называется квадратное уравнение старший коэффициент, которого равен 1.
Кто впервые открыл данную закономерность между значениями
х1 + х2, х1 х2 и коэффициентами квадратных уравнений.
КАРТОЧКА 3
Решите уравнения из таблицы, используя формулы дискриминанта и корней квадратного уравнения.
Заполните таблицу.
Домашнее задание.
ВИД
КОРНИ
Значение х1 + х2
равно
Значение х1 х2
равно
b
с
х2 – 3х – 10 = 0
х2 + 7х + 10 = 0
х2 + 6х + 5 = 0
. Найдите закономерность между значениями
х1 + х2, х1 х2 и коэффициентами квадратных уравнений. Заполните пропуски в выводе
ВЫВОД: Если в квадратном уравнении первый коэффициент а = ___ ,
D 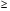 0 и то для корней этого уравнения выполняется условие
0 и то для корней этого уравнения выполняется условие
х1 + х2_= _____, х1 х2 =_______________.
Узнай, как называется квадратное уравнение старший коэффициент, которого равен 1.
4. Кто впервые открыл данную закономерность между значениями
х1 + х2, х1 х2 и коэффициентами квадратных уравнений.
КАРТОЧКА № 1.
ГРУППА № 4. Ученик:_____________________________________
Время.
2 мин.
2 мин.
3 мин.
2мин.
4 мин.
Выполняемая работа.
Задание 1.
Найдите ошибку в решении.
3х2 – 7х – 6 = 0
D= b2 - 4ac; D = (-7)2 – 4 3 (- 6) = 49 + 72 = 121>0, 2 корня
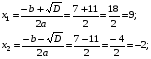
Ответ: х1= 9, х2 = -2,
Задание 2.
Обсуждение с учителем результатов задания 1.
Задание 3.
Решите уравнение, используя формулы дискриминанта и корней квадратного уравнения.
3х2 + 8х + 5 = 0
______________________________________
_______________________________________
_______________________________________
Ответ: ___________________
По окончании решения найди на парте звездочку со своим ответом, если звездочки с твоим ответом нет, то твое решение неверное, найди ошибку.
Задание 4.
Выпиши значения коэффициентов квадратного уравнения из задания 3
а =_________b= с =________
проверьте, выполняется ли для этих коэффициентов равенство:
а – b + с = 0_________________________________________
Задание 5.
Используя результаты решения товарищей по группе, заполните на КАРТОЧКЕ 2 колонку, обозначенную ГРУППА 2 и 4.
КАРТОЧКА № 1.
ГРУППА № 3. Ученик:_____________________________________
Время.
2 мин.
3 мин.
3 мин.
2мин.
3 мин.
Задание.
1. Найдите ошибку в решении.
6х2 + 13х – 2 = 0
D= b2 - 4ac; D = 132 – 4 6 (- 2) = 169 – 48 = 121>0, 2 корня
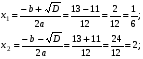
Ответ: х1 =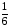 , х2= - 2.
, х2= - 2.
Обсуждение с учителем результатов пункта 1.
2. Решите уравнение, используя формулы дискриминанта и корней квадратного уравнения.
х2 – 9х + 20 = 0
______________________________________
_______________________________________
_______________________________________
Ответ: ___________________
3. Найдите значения выражений
х1 + х2_= ____ х1 х2 =______________,
где х1 и х2 корни уравнения из пункта 2._______
Сравни получившиеся результаты с коэффициентами квадратного уравнения из пункта 2..
4. Обсуди со своими с товарищами по группе результаты получившиеся после сравнения пунктов 2 и 3 у тебя и у них. Найдите закономерность и запишите вывод.
Вывод: Если в квадратном уравнении первый кэффициент
а = ___ , D > 0 и то для корней этого уравнения выполняется
условие х1 + х2_= _____, х1 х2 = _______________.
Выступление одного участника группы с докладом о получившемся выводе.
3х – 5 = 0
2х2 – 5х + 3 = 0
4х2 + 5 = 0
7х2 – 6х = 1
5х - 2х2 + 3 = 0
4х2 – 7х + 3 = 4х2
х3 + 2х = 0
Деяние есть
живое единство
теории и практики.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ