Конспект урока по Математике "Решение уравнений методом подстановки"
Открытый урок по теме:
Решение уравнений методом подстановки
Учитель математики ГОУ гимназии № 1549 Шмелева Ирина Дмитриевна
Г. Москва январь 2013г.
Цели урока:
Образовательная:
формирование навыков решения уравнений повышенной сложности методом подстановки.
Развивающая:
развитие памяти, любознательности, познавательного интереса учащихся, умения преодолевать трудности при решении задач.
Воспитательная:
воспитание аккуратности, наблюдательности, настойчивости в учебе, умение видеть красивое и удивительное вокруг нас.
Задачи урока:
Закрепление и отработка навыков решение уравнений методом введения новой переменной.
Методы:
Преобразовательный (при усвоении учащимися и творческом применении навыков и умений в процессе выполнения упражнений проблемных заданий).
I.Объяснение нового материала.
Метод замены переменной ( или, иначе, метод введения нового неизвестного) состоит в следующем. Предположим , что уравнение f(x)=p(x). Удалось переписать в виде f((g(x))= p(g(x)).
Решение уравнения f(x)=p(x) проведем в два этапа:
Будем считать, что g(x)=u, решим уравнение f(u)=p(u).
Последовательно решим уравнение g(x)=u
 , g(x)= u
, g(x)= u ,…, g(x)=u
,…, g(x)=u .
.
Полученные корни и будут корнями уравнения f(x)=p(x).
Схема метода:
f((g(x))=p(g(x))

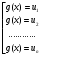 ,где u
,где u , u
, u ,….., u
,….., u корни уравнения f(u)=p(u).
корни уравнения f(u)=p(u).
Введение новой переменной позволяет «разбить задачу на полузадачи», т.е. вместо основного сложного решать несколько простых уравнений.
Пример.
Решить уравнение (х +х+1) (х
+х+1) (х +х+2)=12.
+х+2)=12.
Решение:
Решение:
(х +х+1) (х
+х+1) (х +х+2)=12
+х+2)=12 

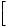
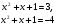

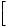
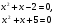

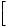
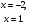
Пусть u=х
 +х+1, тогда исходное уравнение:
+х+1, тогда исходное уравнение:
(u+1)u=12 u
u +u-12=0
+u-12=0
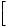
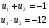

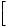
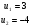
 .
.
х
 +х+5=0,
+х+5=0,
D<0, корней нет.
-Нет ли других замен переменной? (Есть).
II. Домашнее задание:
Решить уравнение, используя метод подстановки:
х
 +х=u;
+х=u;х
 +х+2= u .
+х+2= u .
III. Обобщение нового материала.
В математике существуют целые классы уравнений, которые можно решать этим методом
- биквадратные уравнения;
- дробно-рациональные.
IV. Закрепление материала.
Решить уравнение:
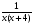 -
-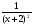 =
=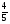 .
.
Решение:
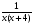 -
-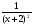 =
=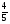

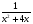 -
-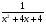 =
=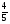

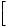
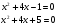


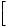
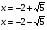 .
.
u =x
 +4x;
+4x;
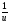 -
-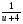 =
=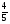

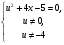



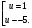

х
 +4х-1=0;
+4х-1=0;
D =
=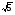 , уравнение имеет два корня;
, уравнение имеет два корня;
х =-2+
=-2+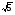 ;
;
х =-2-
=-2-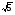 .
.
х
 +х+5=0;
+х+5=0;
D<0, корней нет.
Ответ: -2+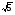 ; -2-
; -2-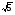 .
.
2. Решить уравнение: х +
+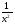 +
+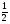 (х-
(х-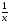 )=5.
)=5.
Решение:
х +
+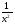 +
+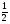 (х-
(х-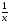 )=5
)=5 


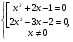


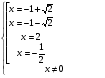

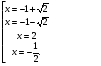
Пусть u = х-
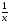 ; u
; u +2= х
+2= х +
+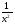 .
.
u +
+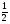 u-3=0
u-3=0 2 u
2 u +u-6=0
+u-6=0
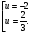
Ответ: -1+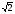 ; -1-
; -1-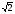 ; 2; -
; 2; -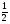 .
.
V. Самостоятельная работа:
1. (х +3х+3)(х
+3х+3)(х -2х+3)=24 х
-2х+3)=24 х .
.
Ответ: 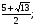
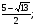 -3+
-3+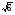 ;-3-
;-3-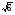 .
.
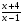 +
+ =
=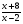 +
+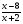 -
-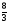 .
.
Ответ: 4;-4;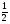 ; -
; -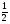 .
.
VI. Домашнее задание.
Решите уравнение методом замены переменной:
х
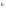 -9х
-9х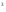 +8=0. Ответ: 1;2.
+8=0. Ответ: 1;2.(х
 +х+4)
+х+4) +8х(х
+8х(х +х+4)+15 х
+х+4)+15 х =0. Ответ: -2; -3;
=0. Ответ: -2; -3; 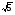 ; -
; -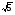 .
.х
 +
+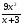 =27. Ответ:
=27. Ответ: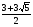 ;
; 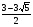 .
.Х(х+3)(х+5)(х+8)=10. Ответ: -4+
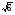 ;-4-
;-4-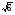 .
.
Анализ усвоения материала и интереса учащихся к теме.
Проверка умения решать основные ключевые задачи при решении уравнений методом введения новой переменной показала , что все учащиеся справились с решением. Они уверенно распознают задачу, безошибочно обосновывают решение.
Часть учеников испытывали неуверенность, но желание деятельности не пропало, поняли , что надо совершенствоваться.
Правильно научились оформлять письменно решение, что поможет школьникам при подготовке к выпускным экзаменам, для формирования уверенности учащихся в своих силах и возможностях. Самостоятельная работа вселила в учеников желание деятельности.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ