Цели урока:

1. Организовать повторение формул тригонометрии, создать условия для совершенствования навыков их применения при различных тригонометрических преобразованиях;

2. Вывести формулы суммы и разности синусов и косинусов;

Формировать практические навыки применения новых формул

ПЛАН – КОНСПЕКТ

урока в 10 классе

«Сумма и разность синусов

и косинусов»

Учитель: Левочкина Анна Николаевна,

МБОУ СОШ № 60 г. Пенза

Тема урока: Сумма и разность синусов и косинусов

Цели урока:

3. Организовать повторение формул тригонометрии, создать условия для совершенствования навыков их применения при различных тригонометрических преобразованиях;

4. Вывести формулы суммы и разности синусов и косинусов;

5. Формировать практические навыки применения новых формул.

Оборудование: таблицы для устной работы, таблицы тригонометрических формул, карточки

Ход урока

I. Организационный момент

II. Проверка домашнего задания №179(2), 180(2,4), 181(2),

№179

№180

№181

1=1

Ученик с места комментирует решение №179(2), указывает, какие формулы применял при решении. У доски 2 ученика работают по карточкам.

Карточка №1

1. Упростить выражение:

Карточка №2

2. Упростить выражение:

Учащиеся поясняют свои преобразования. Каждому учитель задает по одному вопросу дополнительно.

III. Актуализация знаний учащихся.

1. Что называется синусом угла ?

2. Что называется косинусом угла ?

3. Что называется тангенсом угла ?

4. В каких единицах измеряется угол?

5. это? (); это? (); это? (); это? (); это? (); это? (); это? ().

6. Итак, .

7. Какие знаки имеют синус, косинус, тангенс, котангенс?

8. Формулы .

9. Какая точка получается при повороте точки (1;0) на углы и + 2 радиан?

Значит справедливы формулы (одна и та же):

10. Основное тригонометрическое тождество.

11. Как определяется знак перед корнем (знак выражения, стоящего в левой части формулы)?

12. Формулы приведения (правило).

Найди ошибку

Вывешивается плакат

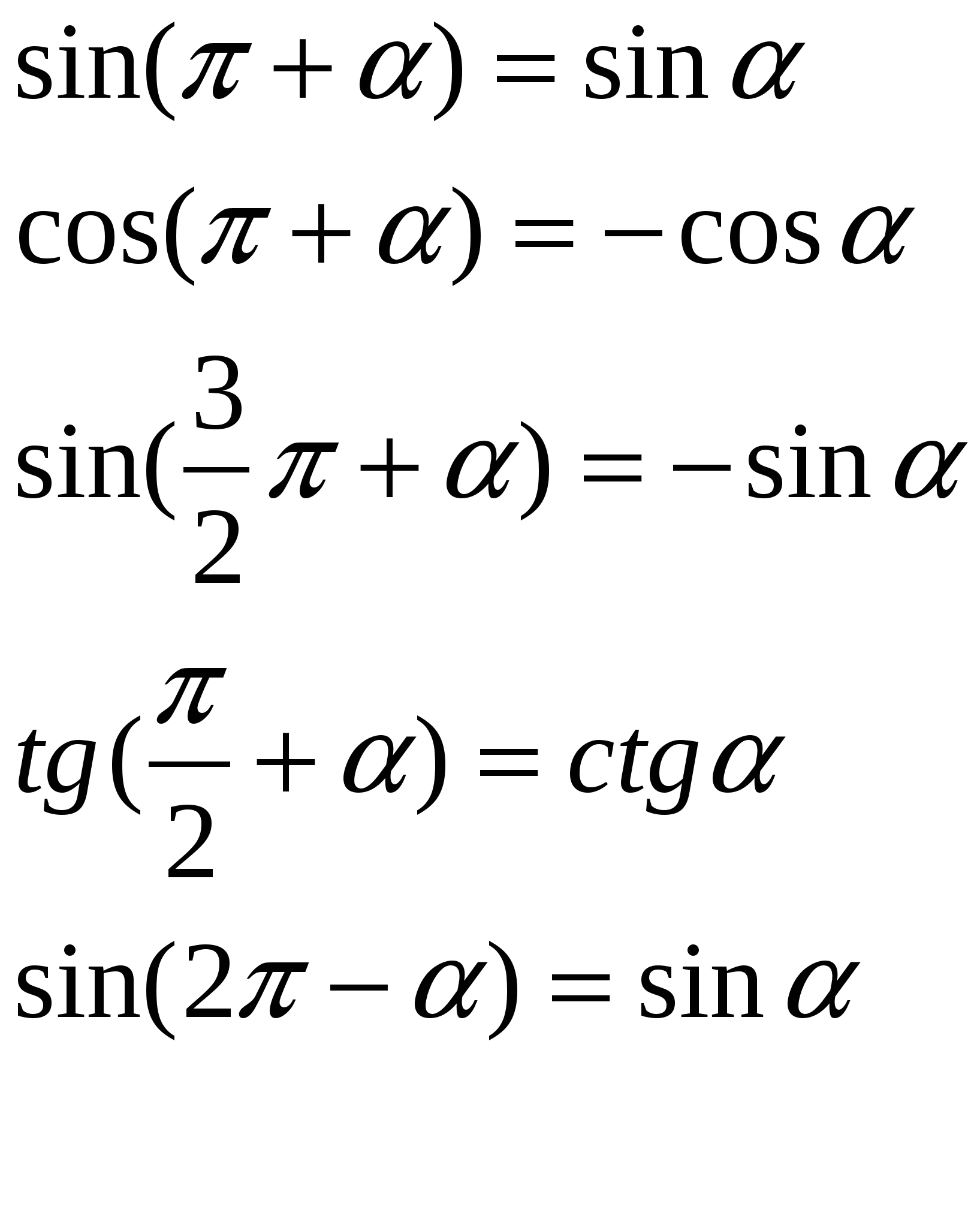
13. Что называется тождеством?

IV. Устная работа

На плакате.

1. Определить четверть, в которой находится точка, полученная поворотом точки (1;0) на угол , если =, , , , , , , .

2. Определить четверть и знак числа , если числа , если ,

V. Открытие новых знаний.

Вспомним формулы .

Вызывается ученик, и выполняется задание у доски.

Упростить выражение:

Ребята, тема сегодняшнего урока «Сумма и разность синусов и косинусов». Я сообщаю вам формулу, по которой мы снова выполним это задание:

(1)

Ученик выходит и решает это задание у доски. Ответ получает тот же.

А теперь выведем эту формулу:

Обозначим = x, = y, тогда x + y = , x – y = , получим

Заменяя в формуле (1) = - получим

Записать эти формулы в справочный материал.

VI. Закрепление

Решение №194(1), 195(1,3)

VII. Итог урока:

- Что нового узнали на уроке?

- Где можно использовать новые знания?

- Оцените свою работу на уроке.

Сообщить оценки за урок.

VIII. Задание на дом: §11, №194(2,4), №195(2,4) - по выбору.