Контрольная работа

по математике за I полугодие

6 класс.

В - 1

1. Выполните действия: .

2. Решите уравнение:

^.

3. Масса курицы равна кг, а масса утки в 2 раза больше. На сколько масса утки больше массы курицы?

4. Даны числа: , , и . Запишите выражение и вычислите его значение: сумма разности первых двух чисел и разности последних двух чисел.

5. Представьте дробь в виде произведения:

1. целого числа и дроби;

2) двух дробей.

В – 2

1. Выполните действия: .

2. Решите уравнение:

^.

3. Масса собаки равна кг, а масса кошки в 3 раза меньше. На сколько масса кошки меньше массы собаки?

4. Даны числа: , , и . Запишите выражение и вычислите его значение: разность суммы первых двух чисел и суммы последних двух чисел.

5. Представьте дробь в виде произведения:

1) целого числа и дроби;

2) двух дробей.

Административная контрольная работа

по математике за I полугодие 5 класс.

В – 1

1. Вычислите: 180  94 – 47700 : 45 + 4946.

2. Задача:

В треугольнике MFK сторона FK равна 62 см, сторона КМ на 1 дм больше стороны FK, а сторона MF – на 16 см меньше стороны FK. Найдите периметр треугольника MFK и выразите его в дециметрах.

3. Решите уравнение:

13y – 6y + 14y = 420.

4. Используя формулу пути S = v  t, найдите:

а) путь, пройденный автомашиной за 3ч, если её скорость 80 км/ч;

б) время движения катера, прошедшего 90 км со скоростью 15 км/ч.

5. Придумайте четырёхзначное число, которое при делении на 36 даёт остаток 31.

В – 2

1. Вычислите: 86  170 – 5793 + 72800 : 35;

2. Задача:

В треугольнике BNP сторона NP равна 73 см, сторона BP на 1 дм меньше стороны NP, а сторона BN – на 11 см больше стороны NP. Найдите периметр треугольника BNP и выразите его в дециметрах.

3. Решите уравнение:

21y + 13y - 17y = 187.

4. Используя формулу пути S = v  t, найдите:

а) путь, пройденный моторной лодкой за 2ч, если её скорость 18 км/ч;

б) скорость движения автомобиля, за 3ч прошедшего 150 км.

5. Придумайте четырёхзначное число, которое при делении на 41 даёт остаток 1.

Административная контрольная работа

по алгебре за I полугодие 7 класс.

В – 1

1. Найдите значение выражения, используя свойства степеней:

3⁷  ( 3² )³ : 3¹⁰

2. Решите уравнение: 30 +5  ( 3х – 1 ) = 35х - 25.

3. Задача:

На базе хранится 590 тонн овощей. При этом картофеля в 2,5 раза больше, чем моркови. Лука на 14 тонн больше, чем картофеля. Сколько тонн картофеля, моркови и лука находится на базе?

4. Упростите выражение и найдите его значение:

2a(a + b) – b(2a – b) – b(b + 1) при а = - 0,3 и b = - 0,4.

5. Постройте в одной системе координат графики функций y = 2 - х и

y = х - 2 и укажите координаты точки их пересечения.

В – 2

1. Найдите значение выражения, используя свойства степеней:

2⁸  ( 2³ )² : 2¹²

2. Решите уравнение: 20 + 4  ( 2х – 5 ) = 14х + 12.

3. Задача:

На базе хранится 520 тонн рыбы. При этом трески в 1,5 раза больше, чем наваги. Окуня на 16 тонн больше, чем трески. Сколько тонн трески, наваги и окуня находится на складе?

4. Упростите выражение и найдите его значение:

с(2а – 2с) + а(3с – а) -2(а – с²) при а = - 0,1 и с = 0,7.

5. Постройте в одной системе координат графики функций y = 0,5x + 1 и

y = - x +4 и укажите координаты точки их пересечения.

Административная контрольная работа по алгебре за I полугодие, 8 класс

Ф.И. учащегося ________________________

Часть 1

В – 1

1. Какое из чисел является иррациональным?

А. Б. В. Г. Все эти числа.

2. Найдите значение выражения при х = .

А. Б. 1 В. Г. При х = выражение не имеет смысла.

3. Соотнесите с соответствующей точкой координатной прямой каждое из чисел:

1) ; 2) ; 3) .

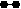
М N P Q

3 4 5 6 7 х

Ответ:

1

2

3

4. Каждый график соотнесите с соответствующей ему формулой:

а) y = ; б) y = 2x ; в) y = 2 – x² ; г) y = 2x + 2.

Ответ:

1

2

3

4

5. Каждое из уравнений соотнесите с множеством его корней.

1) х² = х; 2) х² = -х; 3) х² = -1; 4) х² = 1.

а) 1 и –1; б) 0 и 1; в) 0 и –1; г) корней нет.

Ответ:

1

2

3

4

Часть 2 (В – 1)

6. Сократить дробь: .

7. Упростите выражение .

8. При каком значении a тождественно равны выражения и ?

Оценка

«2»

«3»

«4»

«5»

Часть 1

4

4

4

4

Часть 2

-

1

2

3

Административная контрольная работа по алгебре за I полугодие, 8 класс

Ф.И. учащегося ___________________________

Часть 1

В – 2

1. Какое из чисел является рациональным?

А. Б. В. Г. Ни одно из этих чисел.

2. Найдите значение выражения при х = - 0,17.

А. 0,07 Б. 0,7 В. 1,24 Г. При х = - 0,17 выражение не имеет смысла.

3. Соотнесите с соответствующей точкой координатной прямой каждое из чисел:

1) ; 2) ; 3) .

M N P Q

3 4 5 6 7

Ответ:

1

2

3

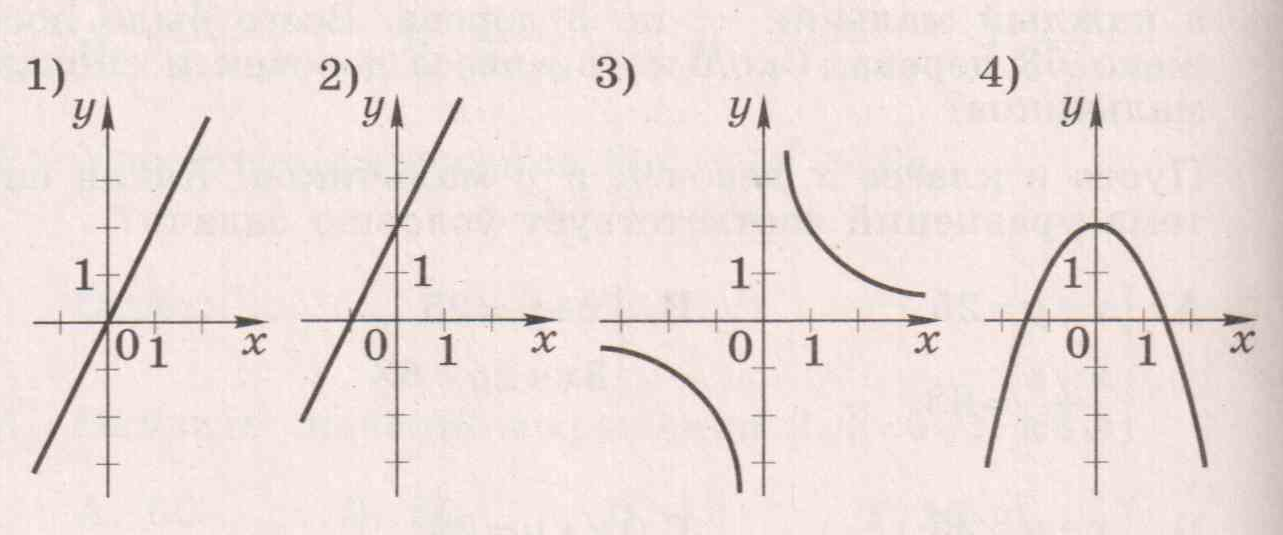
4. Каждый график соотнесите с соответствующей ему формулой:

а) y = ; б) y = x²-1; в) y = – x ; г) y = 1 - x .

Ответ:

1

2

3

4

5. Каждое из уравнений соотнесите с множеством его корней.

1) х² – 1 = 0; 2) х² + 1 = 0; 3) х² = x; 4) х² = -x.

а) 0 и –1; б) 0 и 1; в) 1 и –1; г) корней нет.

Ответ:

1

2

3

4

Часть 2 (В – 2)

6. Сократить дробь: .

7. Упростите выражение .

8. При каком значении a тождественно равны выражения и ?

Оценка

«2»

«3»

«4»

«5»

Часть 1

4

4

4

4

Часть 2

-

1

2 - 3

3 - 4

Контрольная работа

по алгебре и началам математического анализа

за I полугодие 11 класс.

В – 1

1. Найдите множество значений функции:

а) y = sinx – 5; б) y = 4cos2x.

2. Найти область определения функции y = .

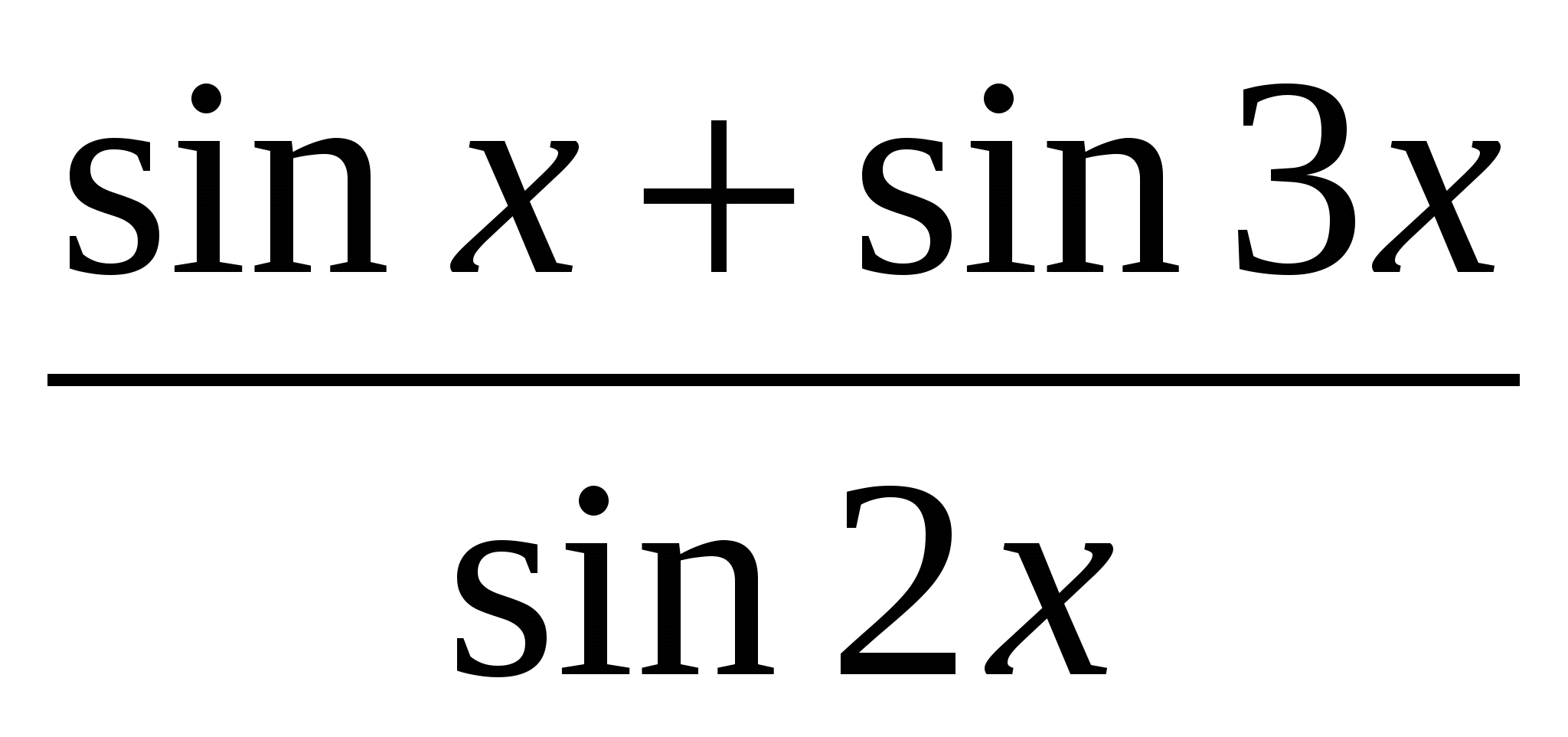3. Найдите производную функции:

а) f(x) = е^x (1 + sinx);

б) h(x) = и вычислите h(2).

2. Напишите уравнение касательной к графику функции f(x) = x² – 2x в точке его с абсциссой х₀ = -1.

2. Функция y = f(x) определена на всей числовой прямой и является периодической с периодом 5. На промежутке ( -1; 4 ] она задаётся формулой f(x) = 1 + 2х – х². Найдите значение выражения

2f(-15) + 3f(18).

В - 2

1. Найдите множество значений функции:

а) y = sinx – 5; б) y = 4cos2x.

2. Найти область определения функции y = .

3. Найдите производную функции:

а) f(x) = 2^x (1 + cosx);

б) h(x) = и вычислите h(4).

4. Напишите уравнение касательной к графику функции f(x) = x² + 2x в

точке его с абсциссой х₀ = -2.

5. Функция y = f(x) определена на всей числовой прямой и является периодической с периодом 5. На промежутке [ -4; 1 ) она задаётся формулой f(x) = -х² –4х -2. Найдите значение выражения

4f(-18) + 3f(18).

Административная контрольная работа по алгебре за I полугодие, 9 кл.

Ф.И. учащегося ___________________________

В – 1

Часть 1

1. Какое из чисел не входит в область определения выражения ?

А. –6 Б. 0 В. 4 Г. 8

2. Каждый график соотнесите с соответствующей ему формулой.

а) y = ; б) y = 2x ; в) y = 2 – x² ; г) y = 2x + 2.

Ответ:

1

2

3

4

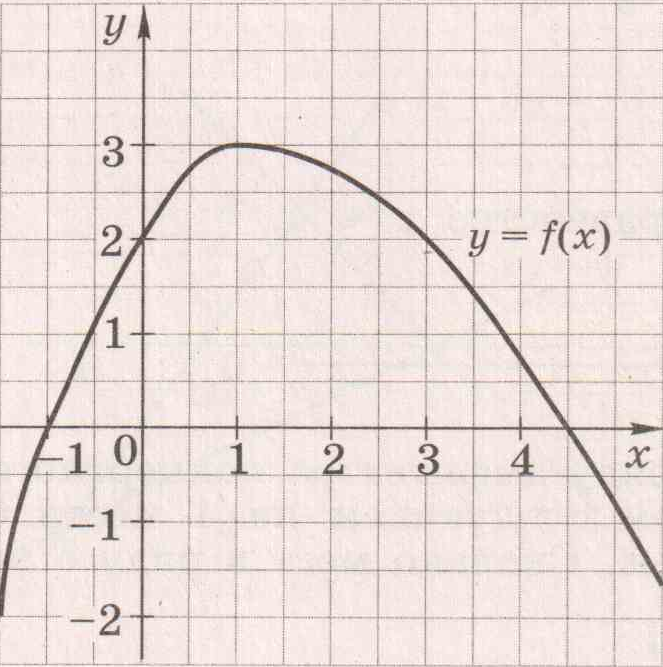
3. На рисунке изображён график функции y = f(x).

Из приведённых утверждений выберите верное.

А. f(-1) > f(3)

Б. Функция y = f(x) убывает на промежутке .

В. f(2) = 0.

Г. Наибольшее значение функции y = f(x) равно 1.

4. Найдите значение выражения .

А. Б. В. 16 Г. –16

Часть 2

5. Найдите значение выражения а² - 6а – 1 при а = + 4.

6. Решите графически уравнение х³ – 2х – 4 = 0.

7. При каких значениях х имеет смысл выражение ?

8. Известно, что парабола y = ax² – 4x + 2 проходит через точку D(3; 1). Найдите коэффициент а. Пересекает ли эта парабола ось х?

Административная контрольная работа по алгебре за I полугодие, 9 кл.

Ф.И. учащегося ____________________________

В – 2

Часть 1

1. Какое из чисел не входит в область определения выражения ?

А. 2 Б. 0 В. -4 Г. -2

2. Каждый график соотнесите с соответствующей ему формулой.

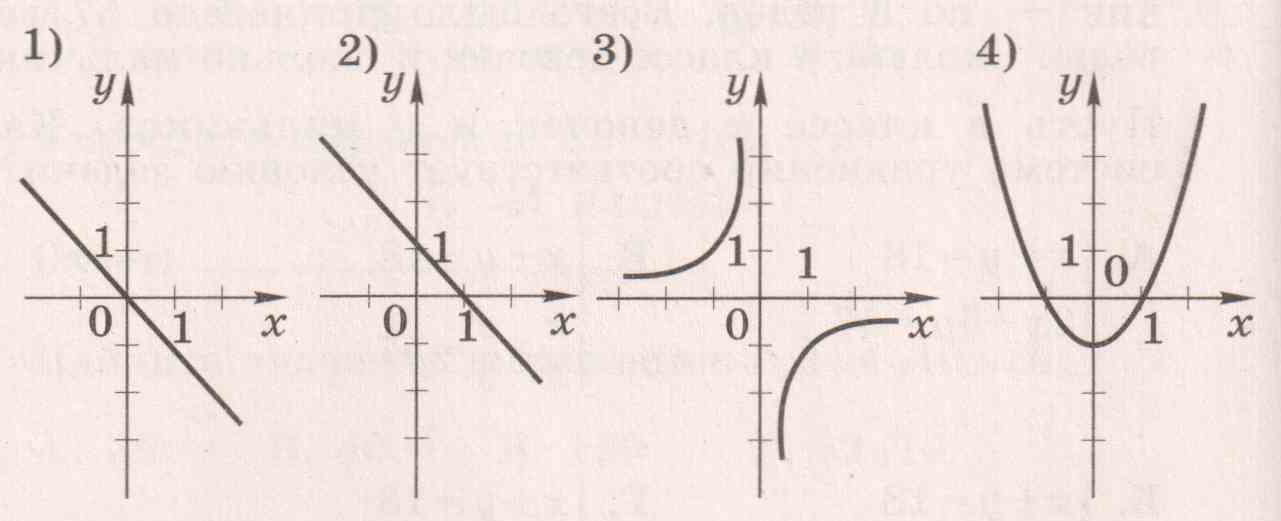
а) y = ; б) y = x²-1; в) y = – x ; г) y = 1 - x .

Ответ:

1

2

3

4

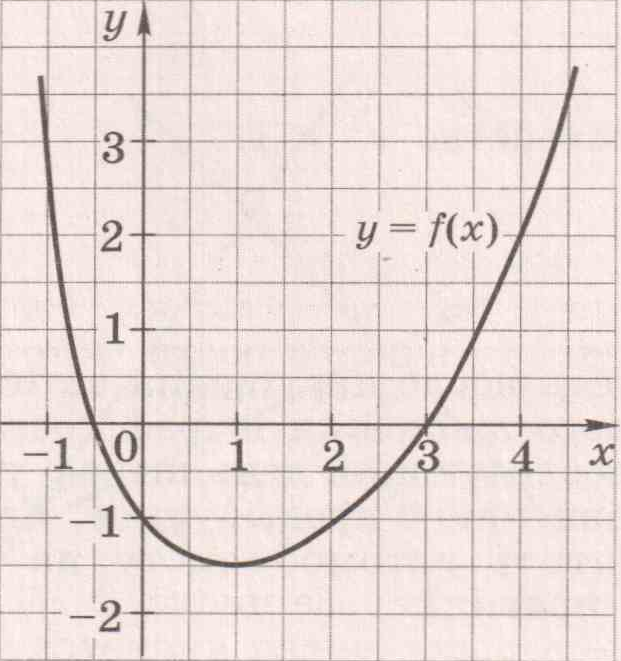
3. На рисунке изображён график функции y = f(x).

Из приведённых утверждений выберите верное.

А. f(-1) < f(2)

Б. Функция y = f(x) убывает на промежутке .

В. f(0) = 2.

Г. Функция принимает наименьшее значение при х = 3.

4. Найдите значение выражения .

А. 6 Б. В. Г. –6

Часть 2

5. Найдите значение выражения с² - 4с + 2 при с = - 3.

6. Решите графически уравнение х³ – 2х + 4 = 0.

7. При каких значениях х имеет смысл выражение ?

8. Известно, что парабола y = 2x² + bx + 3 проходит через точку В(2; 9). Найдите коэффициент b. Пересекает ли эта парабола ось х?

Административная контрольная работа по алгебре и началам математического анализа за I полугодие

10 класс.

В – 1

1. Вычислить: .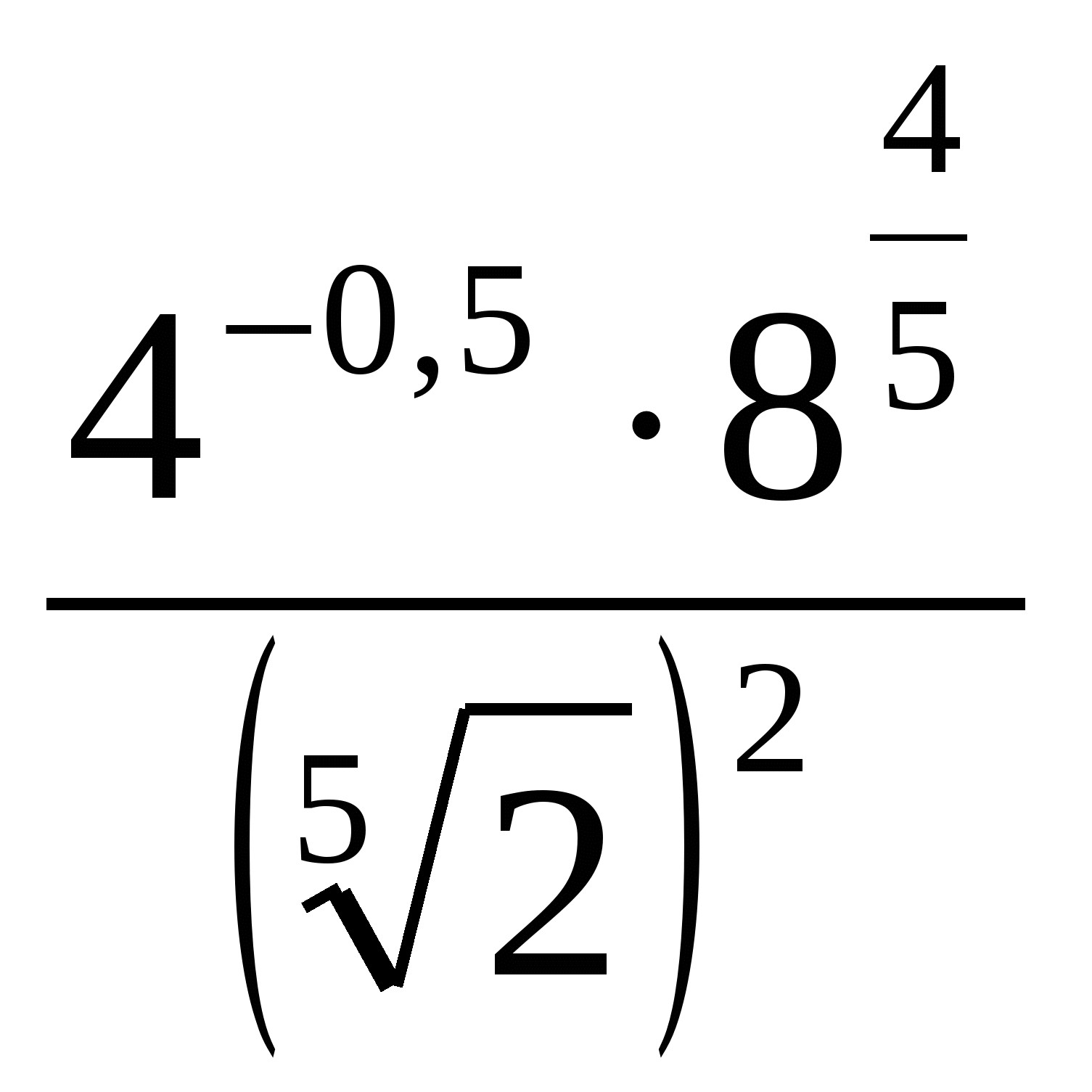

2. Какому интервалу принадлежит корень уравнения :

1) ( - 5; - 3] 2) ( - 3; 3 ) 3) [ 3; 4 ) 4) [ 4; 17 )

3. Найдите область определения функции :

1) [ 3; + ) 2) [ - 4; 3 ] 3) x = 3 4) ( - ; - 4]  [ 3; +  )

4. Наименьший из корней уравнения равен:

1) – 3 2) – 2 3) 1 4) – 1

5. Укажите число натуральных решений неравенства:

1) 3 2) 4 3) 6 4) число бесконечно

В – 2

1. Вычислить: .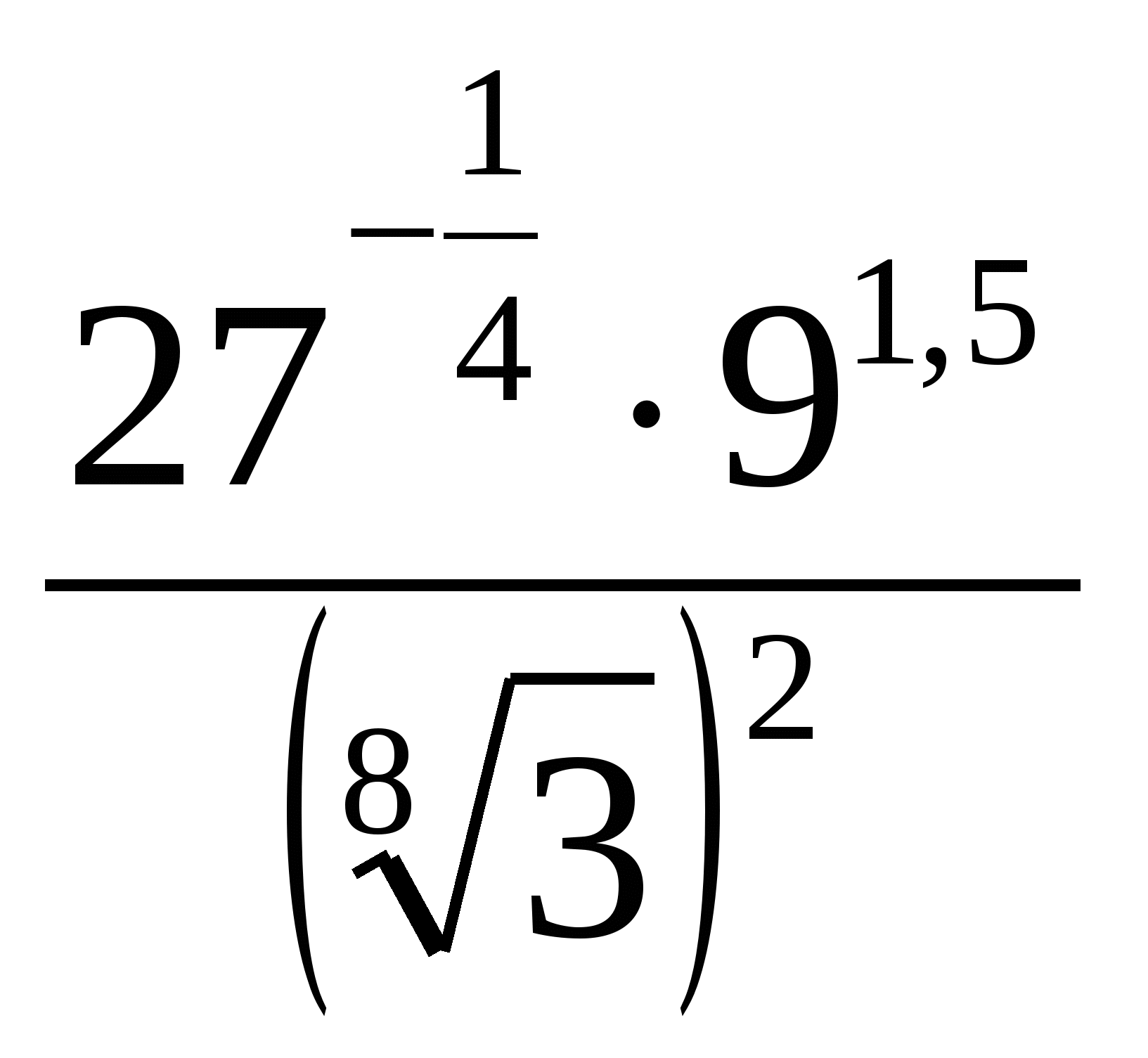

2. Какому интервалу принадлежит корень уравнения :

1) [ - 5; - 3] 2) ( - 3; 0 ] 3) [ 0; 4 ] 4) ( 4; 20 )

3. Найдите область определения функции :

1) (- ; - 3]  [ 0,5; + ) 2) [ - 3; 0,5 ] 3) (- ; + ) 4) ( - ; - 2,5]  [ 0; +  )

4. Все корни уравнения принадлежат отрезку:

1) [ - 4; - 1] 2) [ - 1; 1 ] 3) [ - 2; 0 ] 4) [ 1; 3 ]

5. Сколько натуральных чисел являются решениями неравенства ?

1) 0 2) 1 3) 2 4) бесконечное множество