Курсовая работа «Организация работы над текстовой задачей как средство формирования логических умений младших школьников»

Министерство образования и науки Волгоградской области

Государственное бюджетное образовательное учреждение дополнительного профессионального образования (повышения квалификации) специалистов

«Волгоградская государственная академия повышения квалификации и переподготовки работников образования»

(ГБОУ ДПО «ВГАПКиПРО»)

Кафедра начального образования

Курсовая работа

«Организация работы над текстовой задачей как средство формирования логических умений младших школьников»

Выполнил: слушатель курсов № 210

учитель начальных классов МКОУ Песковатская СОШ Дубовского района Волгоградской области

Лукьяненко Светлана Геннадьевна

Проверил: старший методист кафедры начального образования ВГАПКиПРО, магистр педагогики

Казачкова Светлана Петровна

Волгоград – 2012 год

Содержание работы:

Введение…………………………………………………………………………

Глава I. Организация работы над текстовыми задачами в начальной школе……………………………………………………………………………

1.1. Понятие «текстовые задачи», классификация текстовых задач……….

1.2. Методы и формы работы над текстовыми задачами……..……………...

Глава II. Педагогический опыт по организации работы над текстовыми задачами…………………..…………………………………….

2.1 Описание опыта работы над текстовыми задачами по УМК «Школа России»……………….……………………………………………………...….

2.2. Методические рекомендации по организации работы над текстовыми задачами…………………………………..……………………………………..

Заключение……………………………………………………………………..

Литература……………………………………………………………………...

Приложения:

Конспект урока математики по теме «Задача».

Алгоритм решения задачи

Тесты « Решение задач»

Введение

Ребенок с первых дней занятий в школе встречается с задачей. Сначала и до конца обучения в школе математическая задача неизменно помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. В тоже время решение задач способствует развитию логического мышления.

Как обучать детей нахождению способа решения текстовой задачи? Этот вопрос – центральный в методике обучению решения задач. Для ответа на него в литературе предложено немало практических приемов, облегчающих поиск способа решения задачи. Однако теоретические положения относительного нахождения пути решения задачи остаются мало разработанными.

Особенности текста задачи могут определить ход мыслительного процесса при ее решении. Как сориентировать детей на эти особенности? Знание ответов на них составляют теоретико-методические положения, на основе которых можно строить конкретную методику обучения; они помогут определить методические приемы поиска способов решения задачи, в том числе решения различными способами.

Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала. Решая их, учащиеся приобретают математические знания, готовятся к практической деятельности. Задачи способствуют развитию их логического мышления.

Исходя из вышеизложенного необходимо выделить следующее:

Цель работы: разработать алгоритм действия по организации работы с текстовыми задачами.
Объект исследования: образовательный процесс в начальной школе.
Предмет исследования: формы и методы работы над текстовыми задачами.
Задачи исследования:

- рассмотреть понятие «текстовые задачи», виды текстовых задач;

- проанализировать формы и методы работы над текстовой задачей;

- описать опыт работы над текстовой задачей;

- разработать педагогические рекомендации по организации работы над текстовыми задачами.

Методы исследования: анализ методической литературы, систематизация видов текстовых задач, определение эффективных форм и методов работы над текстовыми задачами.

Глава 1. Организация работы над текстовыми задачами в начальной школе.

1.1 Понятие «текстовые задачи», классификация текстовых задач.

Текстовая задача – это описание некоторой ситуации на естественном языке, с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами и определить вид этого отношения.
Любая текстовая задача состоит из двух частей – условия и требования (вопроса). В условии соблюдаются сведения об объектах и некоторые числовые данные объекта, об известных и неизвестных значениях между ними. Требования задачи – это указание того, что нужно найти. Оно выражено предложением в повелительной или вопросительной форме.
Ученик должен, прежде всего, осознать, что такое текстовая задача. И целью подготовительного периода является возможность показать перевод различных реальных явлений на язык математических символов и знаков.
При введении термина «задача» следует опираться на разные упражнения с той целью, чтобы показать отличие задачи от упражнений, которые они выполняли по картинке. [5, c. 266]

Единой классификации не существует. Классификация на простые и составные компоненты (2 и более действия). Простые задачи Бантова М.А. делит на группы в зависимости от понятий, которые формируются при ее решении.

К первой группе относятся простые задачи, при решении которых дети усваивают конкретный смысл каждого из арифметических действий, т. е. дети устаивают, какое арифметическое действие соответствует той или иной операции над множествами. В этой группе пять задач:

1) Нахождение суммы двух чисел;

2) Нахождение остатка;

3) Нахождение суммы одинаковых слагаемых (произведения);

4) Деление на равные части;

5) Деление по содержанию.

Ко второй группе относятся простые задачи, при решении которых учащиеся усваивают связь между компонентами результатами арифметических действий. К ним относятся задачи на нахождение неизвестных компонентов.

1) Нахождение первого слагаемого по известным сумме и второму слагаемому;

2) Нахождение второго слагаемого по известным сумме и первому слагаемому;

3) Нахождение уменьшаемого по известным вычитаемому и разности;

4) Нахождение вычитаемого по известным уменьшаемому и разности;

5) Нахождение первого множителя по известным произведению и второму множителю;

6) Нахождение второго множителя по известным произведению и первому множителю;

7) Нахождение делимого по известным 'делителю и частному;

Неизвестное число разделили на 9 и получили 4. Найти неизвестное число.

8) Нахождение делителя по известным делимому и частному.

К третьей группа относятся задачи, при решении которых раскрывается новый смысл арифметических действий. К ним относятся простые задачи, связанные с понятием разности, и простые задачи, связанные с понятием отношения (6 видов).

1) Разностное сравнение чисел или нахождение разности двух чисел (I вид).

Один дом построили за 10 недель, а другой за 8 недель. На сколько недель больше затратили на строительство первого дома?

2) Разностное сравнение чисел или нахождение разности двух чисел (II вид).

Один дом построили за 10 недель, а другой за 8. На сколько недель меньше затратили на строительство второго дома?

3) Увеличение числа на несколько единиц (прямая форма).

4) Увеличение числа на несколько единиц (косвенная форма).

5) Уменьшение числа на несколько единиц (прямая форма).

6) Уменьшение числа на несколько единиц (косвенная форма).

Назовем задачи, связанные с понятием отношения.

1) Кратное сравнение чисел или нахождение отношения двух чисел (I вид).

Колхоз купил 24 сеялки и 8 тракторов. Во сколько раз больше купили сеялок, чем тракторов?

2) Кратное сравнение чисел или нахождение отношения двух чисел (II вид).

3) Увеличение числа в несколько раз (прямая форма).

4) Увеличение числа в несколько раз (косвенная форма).

5) Уменьшение числа в несколько раз (прямая форма).

6)'Уменьшение числа в несколько раз (косвенная форма).

Для составных задач выделить единую классификацию не представляется возможным. Составные задачи Бантова делит на:

1) задачи, в которой нет тройки взаимосвязанных величин

2)задачи с пропорциональными величинами:

а) задачи на нахождение 4-го пропорционального;

б) задачи на нахождение неизвестного по 2 разностям;

в) задача на пропорциональное деление;

г) задачи связанные с движением.

В зависимости от соответствия понятия «задача» выделяют следующие виды:

1) задача-вопрос;

2) задачи с недостающим составом условия;

3) задачи с излишним составом условия;

4) с несформированным вопросом;

5) логические задачи;

6) с разным методом решения. . [4, c. 171]

Работа по формированию умения решать текстовые задачи начинается с первых дней обучения в школе. Первые шаги при решении простых задач не вызывают у учащихся затруднений. Но самостоятельное решение составных задач оказывается не по силам многим, и от класса к классу эти учащиеся испытывают всё большие трудности. Причина возникающих затруднений состоит в том, что у учащихся не сформировано в значительной степени умение анализировать текст задачи, правильно выделять известное и неизвестное, устанавливать взаимосвязь между ними, которая является основой выбора действия для решения текстовой задачи.

Методы и формы работы над текстовыми задачами.

Сам процесс решения задач при определенной методике оказывает весьма

положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения, обобщения. Так, при решении любой задачи ученик выполняет анализ: отделяет вопрос от условия, выделяет данные и искомые числа; намечая план решения, он выполняет синтез, пользуясь при этом конкретизацией (мысленно рисует условие задачи), а затем абстрагированием (отвлекаясь от конкретной ситуации, выбирает арифметические действия); в результате многократного решения задач какого-либо вида ученик обобщает знания связей между данными и искомым в задачах этого вида, в результате чего обобщается способ решения задач этого вида.

Задачи выполняют очень важную функцию в начальном курсе математики – они являются полезным средством развития у детей логического мышления, умения проводить анализ и синтез, обобщать, абстрагировать и конкретизировать, раскрывать связи, существующие между рассматриваемыми явлениями.

Решение задач – упражнения, развивающие мышление. Мало того, решение

задач способствует воспитанию терпения, настойчивости, воли, способствует пробуждению интереса к самому процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.

Овладение основами математики немыслимо без решения и разбора задачи, что является одним из важных звеньев в цепи познания математики, этот вид занятий не только активизирует изучение математики, но и прокладывает пути к глубокому пониманию её. Работа по осознанию хода решения той или иной математической задачи даёт импульс к развитию мышления ребенка. Решение задач нельзя считать самоцелью, в них следует видеть средство к углублённому изучению теоретических положений и вместе с тем средство развития мышления, путь осознания окружающей действительности, тропинку к пониманию мира.

Общепризнанно, что для выработки у учащихся умения решать задачи,

важна всесторонняя работа над одной задачей, в частности, и решение её

различными способами.

Следует отметить, что решение задач различными способами позволяет

убедиться в правильности решения задачи даёт возможность глубже раскрыть зависимости между величинами, рассмотренными в задаче.

Возможность решения некоторых задач разными способами основана на различных свойствах действий или вытекающих из них правила.

При решении задач различными способами ученик привлекает дополнительную информацию, поскольку он непроизвольно выполняет в большем числе выборы суждений, хода мысли из нескольких возможных; рассматривается один и тот же вопрос с разных точек зрения. При этом полнее используется активность учащихся, прочнее и сознательнее запоминается материал. Как правило, различными способами решается те из задач, где этого требует вопрос, поэтому такая работа носит эпизодический характер.

В качестве основных в математике различают арифметический и алгебраический способы решения задач. При арифметическом способе ответ на вопрос задачи находится в результате выполнения арифметических действий над числами. Арифметические способы решения задач отличаются друг от друга одним или несколькими действиями или количеством действий, также отношениями между данными, данными и искомым, данными и неизвестным, положенными в основу выбора арифметических действий, или последовательностью использования этих отношений при выборе действий. При алгебраическом способе ответ на вопрос задачи находится в результате составления и решения уравнения. В начальной школе алгебраический способ почти не используется. [15, c. 46]

Опираясь только на чертёж, легко можно дать ответ на вопрос задачи.

Такой способ решения называется графическим.

До настоящего времени вопрос о графическом способе решения арифметических задач не нашёл должного применения в школьной практике.

Графический способ даёт возможность более тесно установить связь между арифметическим и геометрическим материалами, развить функциональное мышление детей.

Следует отметить, что благодаря применению графического способа в

начальной школе можно сократить сроки, в течение которых ученик научится решать различные задачи. В то же время умение графически решать задачу – это важное политехническое умение.

Графический способ даёт иногда возможность ответить на вопрос такой

задачи, которую дети ещё не могут решить арифметическим способом и которую можно предлагать во внеклассной работе. [14, c.26]

Решение задач различными способами – дело непростое, требующее

глубоких математических знаний, умения отыскивать наиболее рациональные решения.

Решение текстовых задач – это сложная деятельность, содержание которой зависит как от конкретной задачи, так и от умений решающего. Тем не менее, в ней можно выделить несколько этапов:

1. Ознакомление с содержанием задачи;

2. Поиск решения задачи;

3. Выполнение решения задачи;

4. Проверка решения задачи. [9, c. 23]

Выделенные этапы органически связанны между собой, и работа на каждом этапе ведётся на этой ступени преимущественно под руководством учителя.

Ознакомиться с содержанием задачи – значит, прочитав её, представить

жизненную ситуацию, отраженную в задаче. Читают задачу, как правило, дети.

Очень важно научить детей правильно читать задачу: делать ударение на

числовых данных и на словах, которые определяют выбор действия, таких, как «было», «уехали», «осталось», «стало поровну» и т.п., выделять интонацией вопрос задачи.

Задачу дети читают один – два, а иногда и большее число раз, но

постепенно их надо приучать к запоминанию задачи с одного чтения, так как в этом случае они будут сразу читать задачу более сосредоточенно.

После ознакомления с содержанием задачи можно приступить к поиску её решения: ученики должны выделить величины, входящие в задачу; данные и искомые числа, установить связи между данными и искомым и на этой основе выбрать соответствующие арифметические действия.

Выделяются несколько приёмов поиска решения задачи.

Иллюстрация задачи – это использование средств наглядности для выявления величин, входящих в задачу, данных и искомых чисел, а также для установления связей между ними. [ 5, c.294]

Иллюстрация может быть предметной и схематической. В первом случае используются для иллюстрации либо предметы, либо рисунки предметов, о которых идёт речь в задаче: с их помощью иллюстрируется конкретное содержание задачи.

Предметная иллюстрация помогает создать яркое представление той

жизненной ситуации, которая описывается в задаче, что в дальнейшем послужит отправным моментом для выбора действия. Предметной иллюстрацией пользуются только при ознакомлении с решением задачи нового вида и преимущественно в 1 классе.

Начиная с 1 класса, используется и схематическая – это краткая запись

задачи.

В краткой записи фиксируются в удобнобразной форме величины, числа данные и искомые, а также некоторые слова, показывающие, о чём говорится в задаче: «было», «положили», «стало» и т.п., и слова, обозначающие отношения: «больше», «меньше», «одинаковая» и т.п.

Краткую запись задачи можно выполнять в таблице и без неё, а также в форме чертежа.

Иллюстрацию в виде чертежа целесообразно использовать при решении задач, в которых даны отношения значений величин (больше, меньше, столько же), а также при решении задач, связанных сдвижением. При этом надо соблюдать указанные в условии отношения: большее расстояние изображать

большим отрезком.

Чертеж наглядно иллюстрирует отношение значений величин, а в задачах на движение схематически изображает соответствующую ситуацию.

Любая из названных иллюстраций только тогда поможет ученикам найти решение, когда её выполняют сами дети, поскольку только в этом случае они будут анализировать задачу сами.

Дети могут установить связи между данными и искомым и выбрать

соответствующее арифметическое действие только с помощью учителя. В этом случае учитель проводит специальную беседу, которая называется разбором задачи.

При разборе задачи нового вида учитель должен в каждом отдельном

случае поставить детям вопросы так, чтобы навести их на правильный или

осознанный выбор арифметических действий.

Очень важно чтобы вопросы не были подсказывающими, а вели бы к самостоятельному нахождению пути решения задачи.

Разбор задачи заканчивается составлением плана решения. План решения – это объяснение того, что узнаём, выполнив то или иное действие, и указания по порядку арифметических действий.

Часто при введении задач нового вида ученики затрудняются

самостоятельно составить план решения, тогда им помогает учитель. В этом случае рассуждение можно строить двумя способами: идти от вопроса задачи к числовым данным или от числовых данных идти к вопросу.

Решение задачи – это выполнение арифметических действий, выбранных при составлении плана решения. При этом обязательны пояснения, что находим, выполняя каждое действие.

Решение задачи может выполняться устно и письменно. При устном решении соответствующие арифметические действия и пояснения выполняются устно. Решение почти половины всех задач должно выполняться в начальных классах устно. При этом надо учить детей правильно и кратко давать пояснения к выполненным действиям.

Проверить решение задачи – значит установить, что оно правильно или

ошибочно.

В начальных классах используются четыре вида проверки:

1. Составление и решение обратной задачи. Если при решении обратной

задачи в результате получится число, которое было известно в данной задаче,

то можно считать, что данная задача решена правильно. Он применим к любой задаче, лишь бы обратная задача была посильна детям, а поэтому им надо указывать, какое число можно брать искомым в обратной задаче.

2. Установления соответствия между числами, полученными в результате решения задачи и данными числами. При проверке решения задачи этим способом выполняют арифметические действия над числами, которые получаются в ответе на вопрос задачи, если при этом получатся числа, данные в условии задачи, то можно считать, что задача решена правильно. Его целесообразно применять для проверки решения задач такой структуры, в которых можно получить числа, данные в задаче, путём выполнения соответствующих действий над числами, полученными в ответе.

3. Решение задачи другим способом.

Если задачу можно решить различными способами, то получение одинаковых результатов подтверждает, что задача решена правильно. Два способа нельзя считать различными, если они отличаются только порядком выполнения действий.

4. Прикидка ответа.

Применение этого способа состоит в том, что до решения задачи

устанавливается область значений искомого числа, т.е. устанавливается,

больше или меньше какого-то из данных чисел должно быть искомое число. После решения задачи определяется, соответствует ли полученный результат установленной области значений, если он не соответствует установленным границам, значит, задача решена неправильно. [14, c.42]

Таким образом, этот способ помогает заметить ошибочность решения, но он не исключает других способов проверки решения задач.

Глава II. Педагогический опыт по организации работы над текстовыми задачами.

2.1 Описание опыта работы над текстовыми задачами по УМК «Школа России».

В математике УМК «Школа России», по которому я работаю, знакомство с простыми задачами начинается в 1-ом классе при изучении чисел первого десятка. Это задачи на сложение и вычитание. Во 2-ом классе при изучении новых арифметических действий (умножение и деление) ребята знакомятся и с новыми задачами, при решении которых используются эти действия. В 3-eм классе ведется работа по закреплению умений решать задачи в одно, два или три действия; происходит знакомство с задачами на нахождение доли числа; решаются задачи с величинами: цена, количество, стоимость. В 4-ом классе к новым видам задач относятся задачи, сформулированные в косвенной форме и задачи, с помощью которых раскрывается связь между величинами, например, скоростью, временем и расстоянием.

Поспешное и поверхностное отношение детей к обдумыванию решения задачи начинает складываться ещё в 1 классе. Из опыта знаю, что сразу же после ознакомления с содержанием задачи ребёнок спешит назвать ответ и только по требованию учителя сообщает решение задачи. Ошибки при этом маловероятны, потому что сюжеты задач близки жизненному опыту детей, числа в условии небольшие и, следовательно, нужное арифметическое действие и число – ответ можно найти даже по представлению, не прибегая к вычислениям. Решение задач кажется первокласснику совсем не сложным. Зарождается стремление и постепенно формируется прочная привычка сводить всю работу над задачей к простой вычислительной деятельности. Но процесс решения любой текстовой задачи, это известно всем, состоит из нескольких этапов:

Восприятие и первичный анализ задачи.
Поиск решения и составление плана решения.
Выполнение решения и получение ответа на вопрос задачи.
Проверка решения.

Для себя я выделила следующие возможные приёмы выполнения первого этапа решения текстовой задачи:

Разный способ анализа задачи – с вопроса или от данных к вопросу.
Представление жизненной ситуации, которая описана в задаче.

Разбиение текста задачи на смысловые части. Применение этого приёма обеспечивает как понимание содержания задачи, так и запоминание.
Переформулировка текста задачи, т.е. «отбрасывание» несущественных деталей, уточнение и раскрытие смысла задачи.
Моделирование ситуации, описанной в задаче (т.е. краткая запись), с помощью:

а) реальных предметов, о которых идёт речь в задаче;

б) предметных моделей;

в) опорных слов;

г) графических моделей в виде рисунка; схемы;

д) чертежа;

е) таблицы;

На более поздних этапах обучения использую следующие формы работы:

Анализ задач с недостающими или лишними данными.
Составление условия к данному вопросу.
Постановка вопроса к данному условию.

Остановлюсь на иллюстрациях моделирования условия задач:

а) реальные предметы, о которых идёт речь в задаче;

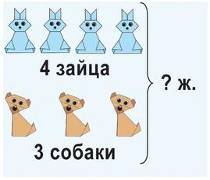
б) предметные модели;

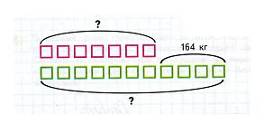
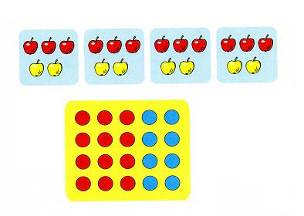
в) опорные слова;

Маша – 7 зн.

Таня – ? на 2 зн. больше

г) графические модели в виде рисунка и схемы;

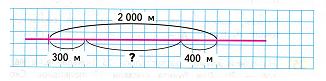
д) чертежи;

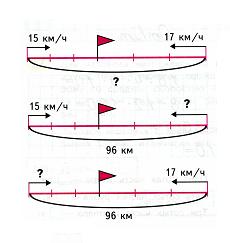
е) таблицы;

Приведу пример работы над условием с недостающими данными или заменой условия (вопроса).

В пенале карандашей, а в коробке на 4 карандаша меньше. Сколько в коробке?
В коробке на 4 карандаша больше, чем в пенале. Сколько карандашей в пенале?

- Предлагаю учащимся данные, которыми можно дополнить условие задачи, чтобы ответить на ее вопрос. Среди них есть и провокационные.

В пенале 7 карандашей.
В пенале на 6 карандашей больше.
В коробке 9 карандашей.
Всего в коробке и пенале 14 карандашей.

2.2 Методические рекомендации по организации работы над текстовыми задачами.

Работая над текстовыми задачами, я выработала следующие рекомендации:

Многие учащиеся только после повторного анализа осознают план решения задачи. Конечно, повторение анализа требует времени, но это окупается.
Необходимо анализировать готовое решение задачи.
Составление различных выражений по данным задачи; объяснение, что обозначает то или иное готовое выражение; выбор тех выражений, которые являются ответом на вопрос задачи.
Сравнения решений нескольких задач.
Запись двух решений на доске – одного верного и другого неверного.
Изменение вопроса задачи, без изменения условия; изменение условия, без изменения вопроса; изменение и того, и другого, ранее решенной

задачи.

Изменение условий задачи так, чтобы задача решалась другим действием, двумя или более действиями.
Завершение начатого решения задачи.
Определение лишнего или недостающего действия в решении задачи.
Составление аналогичной задачи с измененными данными.

Заключение

В данной работе решался ряд задач:

- мы выяснили, что собой представляют текстовые задачи и рассмотрели их классификацию;

- рассмотрели и проанализировали формы и методы работы над текстовой задачей, выявили наиболее эффективные;

- разработали методические рекомендации по работе над текстовыми задачами.

К выше изложенному хочу добавить, что наибольший эффект в развитии школьников в процессе обучения решению задач может быть достигнут в результате систематического использования на уроках математики и внеурочных занятиях специальных задач, направленных на развитие абстрактного и логического мышления. Решение нестандартных задач и задач повышенной сложности расширяет математический кругозор младших школьников и позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.

Написание курсовой работы позволило глубже изучить процесс обучения младших школьников решению текстовых задач и осознать значимость решения задач сначала в начальной школе, а потом и на других ступенях образования. Сначала и до конца обучения в школе сюжетная задача неизменно помогает ученику глубже выяснять различные стороны взаимосвязей в окружающей жизни, расширять свои представления о реальной действительности, учиться решать и другие математические и нематематические задачи.

Литература

1. Алексеева А. В., Бокуть Е. Л., Сиделева Т. Н. Преподавание в начальных

классах: Психолого – педагогическая практика. Учебно-методическое

пособие. – М.: ЦГЛ, 2003. – 208 с.

2. Ануфриев А. Ф., Костромина С. Н. Как преодолеть трудности в обучении детей: Психодиагностические таблицы. Психодиагностические методики. Коррекционные упражнения. – М.: Ось – 89, 2001. – 272 с.

3. Артёмов А.К., Истомина Н.Б. Теоретические основы методики обучения математике в начальных классах: Пособие для студентов факультета тподготовки учителей начальных классов заочного отделения. - М.: Институт практической психологии, Воронеж: НПО «МОДЭК»,1996. – 224 с.

4. Бантова М.А. Методика преподавания математики в начальной школе. – М.: Просвещение, 1984. – 335 с.

5.Белошистая А.В. Методика обучения математике в начальной школе. Курс лекций. – М.: Владос, 2007. – 455 с.

6. Винокурова Н. К. Развиваем способности детей: 2 класс. – М.: Росмэн-

Пресс, 2002. – 79 с.

7. Истомина Н. Б. Методика обучения математике в начальных классах. – М.: ЛИНКА – ПРЕСС, 1997. – 288 с.

8. Лавриненко Т. А. Как научить детей решать задачи: Методические

рекомендации для учителей начальных классов. – Саратов: Лицей, 2000. –

64 с.

9. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова

С. В. Математика: Учебник для 1 класса начальной школы. В 2 частях.

– М.: Просвещение, 2012. – 110 с.

10. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова

С. В. Математика: Учебник для 2 класса начальной школы. В 2 частях.

– М.: Просвещение, 2012. – 96 с.

11. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова

С. В. Математика: Учебник для 3 класса четырёхлетней начальной школы. – М.: Просвещение, 2011. – 112 с.

12. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова

С. В. Математика: Учебник для 4 класса четырёхлетней начальной школы. – М.: Просвещение, 2010. – 112 с.

13. Моро М. И., Пышкало А. М. Методика обучения математике в I –III

классах: Пособие для учителя. Издание второе, переработанное и

дополненное. – М.: Просвещение, 1978. – 336с.

14. Овчинникова В. С. Методика обучения решению задач в начальной школе: Учебное пособие по курсу «Методика обучения математике» для студентов педагогических факультетов высших учебных заведений и колледжей. – М.: Мегатрон, 1998. – 67с.

15. Стойлова Л.П. Математика: Учебник для студентов высших педагогических учебных заведений. – М.: Издательский центр «Академия», 2007. – 432 с.

Приложение

Конспект урока математики по теме «Задача».

(УМК «Школа России», 1 класс)

Цель: Познакомиться с понятием «задача», научиться выделять части задачи.

Задачи:

Предметные:

- Знать структуру текстовой задачи. Знать правило оформления решения задачи в тетради.
- Уметь различать условие задачи, вопрос. Уметь правильно оформлять решение задачи.
- Уметь составлять схему к рисунку, составлять равенство, используя связь целого и частей.

Метапредметные:

Личностные УУД:

-формировать положительное отношение к школе и учебной деятельности, к изучению математики;
- формировать представление о значении математики в жизни человека;
- формировать способность к самооценке на основе критерия успешности учебной деятельности.

Регулятивные УУД:

-формировать умение принимать и сохранять учебную задачу, соответствующую этапу обучения;
- формировать умение оценивать совместно с учителем или одноклассниками результат своих действий;
- овладевать умениями выполнять учебные действия в устной речи;
-в сотрудничестве с учителем, классом находить несколько вариантов решения учебной задачи.
- формировать умение определять и формулировать цель на уроке с помощью учителя;
- проговаривать последовательность действий на уроке;
- работать по коллективно составленному плану;
- планировать своё действие в соответствии с поставленной задачей;
- вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок;
- высказывать своё предположение

Познавательные УУД:

-формировать умение осуществлять анализ, сравнение объекта;
- под руководством учителя проводить классификацию изучаемых объектов;
- под руководством учителя осуществлять обобщение, выводы (подведения под понятие);
-строить небольшие математические высказывания в устной форме (2-3 предложения);
- давать характеристики изучаемым математическим объектам на основе их анализа.
- уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;
- добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке;

Коммуникативные УУД:

- принимать участие в работе парами и группами;
- понимать задаваемые вопросы;
-выражать свою точку зрения;
-адекватно воспринимать другое мнение и позицию.

Оборудование: И К Т и мультимедийная система, диск, карточки с названиями этапов исследования, карточки с выражениями, набор цифр у детей, карточки с названиями составных частей задачи, тексты задач.

Ход урока:

I. Орг. момент. Мотивация к учебной деятельности.

Я рада, что вы собрались здесь, друзья. И думаю, встретились мы не зря. Мы будем учиться сегодня решать, Исследовать, сравнивать и рассуждать,

Секрет математики вновь открывать.

– Сегодня на уроке мы будем внимательно слушать учителя и друг друга, наблюдать, стараться запоминать и понимать.

Девиз нашего урока: «Знаешь – говори, не знаешь – слушай».

- Значит, чему будет посвящён наш урок? (Открытию нового знания)

- Над развитием, каких умений мы будем с вами сегодня работать? (Появляется запись на доске) Уметь

- сравнивать;

- исследовать;

- рассуждать;

- решать;

- обобщать,

- делать выводы…

И так, друзья, в путь! Но для начала, как всегда, нужна гимнастика ума.

чему равна сумма чисел 3 и 2; 4. чему равна сумма чисел 4 и 2;
8 уменьшить на 2; 5. увеличить на 2;
10 уменьшить на 2; 6. 9 уменьшить на 2

II. Подготовка к работе на основном этапе.

Актуализация знаний. Подведение к целеполаганию.

-Послушайте два рассказа и сравните их:

1 .Мишутка нашёл 6 грибочков, а белочка 1 грибочек. Сколько всего грибов нашли звери?

2 Мишутка нашёл 6 грибочков, а белочка 1 грибочек. Мишутка и белочка

– звери, потому что их тело покрыто шерстью.

-Как вы думаете, какой из этих рассказов можно поместить в учебник «Математика», а какой в учебник «Окружающий мир»? (ответы детей)

Такие рассказы в математике называются задачами.

III. Усвоение новых знаний и способов действий.

Формулирование темы и цели урока.

- Кто догадался, о чем пойдет речь сегодня на уроке? (ответы детей)

- А какие цели урока вы себе поставите? (ответы детей)

- Давайте сделаем вывод: главная цель нашего урока: познакомиться с задачами и понять, почему не все рассказы могут быть задачей.

IV. Физкультминутка. «Открывай скорее книжку»

V. Открытие нового знания

- Юные мои математики, не хотите ли узнать ещё что-то о задаче и её составных частях? С этой целью предлагаю провести исследование по теме. В конце урока мы должны получить проект под названием "Задача".

- Давайте наметим наш план действий.

Работа в группах.

1 этап - карточка с восклицательным знаком (надпись "Подумать!")

2 этап - "Узнать из книг" (рисунок книги)

3 этап - "Наблюдение и эксперимент" (рисунок ладони)

4 этап - "Обобщение материала" (нарисован вопросительный знак)

- Все этапы понятны? Желаю удачи!

1 этап - карточка с восклицательным знаком (надпись "Подумать!")

- Найдите задачу! Обсудите свой выбор. Сразу скажу, что в задаче то, что нам известно, называется УСЛОВИЕМ. А то, что нужно найти - ВОПРОСОМ задачи. Прочитайте в нашей задаче условие. А теперь вопрос задачи. (На листочках - УСЛОВИЕ, ВОПРОС).

- Давайте проверим это знание вторым этапом.

2 этап - "Узнать из книг" (рисунок книги)

- Из какой книги вы сейчас можете узнать о задаче? (из учебника). С.88 Исследуйте эту страницу и найдите подсказку (чтение по учебнику чему должны научиться).

- Итак, действительно, задача состоит из УСЛОВИЯ, ВОПРОСА.

- Закрепим это знание. Послушайте внимательно (объяснение с диска).

VI. Физкультминутка. «Вновь у нас физкультминутка»

- Давайте выясним точно, что является какой частью задачи. Для этого давайте прочитаем №1 с.88. Закрепим это знание.

3 этап - "Наблюдение и эксперимент" (рисунок ладони)

- Вернемся к нашим полузадачам и проанализируем их: а можем ли мы им помочь превратиться в настоящие задачи? Каких частей не хватает?(ответы детей) - Давайте решим их.

4 этап - "Обобщение материала" (нарисован вопросительный знак)

На листочках и на доске записаны слова столбиком: ЗАДАЧА, УСЛОВИЕ, ВОПРОС, РЕШЕНИЕ, ОТВЕТ

- Если условие неполное, не хватает чисел - можно решить задачу?

- Если нет вопроса, можно ли считать такую запись задачей?

- Посмотрите на доску. Весь собранный материал у нас расположен в строгой последовательности. Это и есть наш проект, который мы должны были составить к концу урока

Задача состоит из условия, вопроса. Задачу можно решить и дать ответ на вопрос. А чтобы правильно ее решить, я предлагаю посмотреть памятку и запомнить.

Памятка

Прочитать задачу
Узнать о чём (ком) задача.
Что об этом известно.
Найти вопрос задачи.
Написать краткое условие.
Решить задачу.
Написать ответ.

Работа в группах:

СОЕДИНИ ВОПРОС С УСЛОВИЕМ ЗАДАЧИ

4 медвежонка РЕШЕНИЕ

На поляне играли 6 медвежат,

2 медвежонка убежали ВОПРОС

Сколько медвежат осталось играть ОТВЕТ

6-2=4 УСЛОВИЕ

VII. Систематизация и самооценка полученных знаний.

- Какие новые знания вы получили на уроке?

1. Самостоятельная работа учащихся в тетрадях на странице 33.

2. Контроль. Сверьте свою работу с работой на доске.

IX. Итог урока. Рефлексия учебной деятельности.

- Какие умения помогли вам сегодня на уроке?

- Какие знания вы использовали и приобрели? Дополняется таблица.

Уметь:

-сравнивать;

-исследовать;

-рассуждать;

- решать;

-группировать;

-анализировать,

-работать в группе, паре.

Знать:

-понятие «задача»;

-части задачи;

Подведем итог урока: - Как одним понятием назвать математический рассказ? (задача)

- Из чего состоит задача? (Условие, вопрос)

Рефлексия:

Я узнал …

Я научился…

Мне понравилось…

Я бы хоте…

Алгоритм решения задачи.

1.Читаю задачу...

2.Известно...

3.Надо узнать...

4.Объясняю...

5.Решаю...

6.Ответ...

7.Проверяю...

Пример решения задачи с использованием памятки

1.Поезд состоял из 12 вагонов. На стоянке несколько вагонов отцепили, и осталось 10 вагонов. Сколько вагонов отцепили?

2.Известно, что было 12 вагонов, несколько отцепили, 10 осталось.

3.Надо узнать, сколько вагонов отцепили.

Было — 12 в.

Отцепили — ?

Осталось — 10 в.

4.Объясняю: отцепили 12 вагонов без 10, которые остались.

5.Решаю: 12 - 10 = 2 (в.)

6.Ответ: 2 вагона отцепили.

7.Проверяю: 10 + 2 = 12 (в.)

Для закрепления умения решать простые задачи ученик составляет задачи по готовому решению, по краткой записи, по рисунку.

Тесты «Решение задач»

I уровень

A. Какое действие следует выбрать, если в задаче поставлен вопрос: «На сколько больше…?»

1) сложение 2) вычитание 3) умножение

Б. Какое действие следует выбрать, если в задаче поставлен вопрос: «На сколько меньше…?»

1) вычитание 2) сложение 3) умножение

В. Как следует продолжить правило? «Чтобы узнать, на сколько одно число больше или меньше другого, надо …»?

1) к меньшему прибавить большее

2) к большему прибавить меньшее

3) из большего вычесть меньшее

Г. Вите 8 лет, Кате – 12. На сколько лет Катя старше Вити?

Какое решение задачи является верным?

1) 12 – 8 = 4 (г.) 2) 12 + 8 = 20 (л.) 3) 8 + 12 = 20 (л.)

Д. Грибник нашёл 11 подосиновиков и 4 подберёзовика. На сколько меньше подберёзовиков, чем подосиновиков нашёл грибник? Какое число является ответом к задаче?

1) 15 2) 8 3) 7

Е. Машина в первый день прошла b км, а во второй – d км. На сколько больше километров прошла машина во второй день, чем в первый? Какой знак будет в выбранном действии в решении задачи?

1) +

2) ○

3) –

II уровень

А. Какая задача решается действием сложения?

1) В саду растёт 5 яблонь, а груш – на 2 меньше. Сколько груш растёт в саду?

2) В саду растёт 5 яблонь и 3 груши. На сколько больше растёт яблонь, чем груш в саду?

3) В саду растёт 5 яблонь и 3 груши. Сколько всего деревьев растёт в саду?

Б. Какая задача решается действием вычитания?

1) Купили 10 кг овощей. Из них 6 кг – картофель, а остальные – морковь. Сколько килограммов моркови купили? 2) Купили 6 кг моркови, это на 2 кг меньше, чем картофеля. Сколько килограммов картофеля купили? 3) Купили несколько килограммов овощей. После того как израсходовали 6 кг, осталось 4 кг. Сколько килограммов овощей купили?

В. Миша поймал □ карасей и ○лещей. На сколько меньше карасей, чем лещей поймал Миша? 9 – 4 = 5 (к.) Какие числа нужно вставить в квадратик и кружочек?

1) 5 и 4 2) 9 и 4 3) 4 и 9

Г. Когда с полки взяли 7 книг, то осталось 6 книг.

Какой вопрос надо поставить к задаче, чтобы она решалась сложением?

1) На сколько больше книг взяли, чем их осталось на полке?

2) Сколько книг взяли?

3) Сколько книг было на полке?

Д. Из коробки взяли 7 цветных и 2 простых карандаша.

Какой вопрос надо поставить к задаче, чтобы она решалась вычитанием?

1) На сколько больше цветных карандашей, чем простых взяли из коробки?

2) Сколько карандашей взяли из коробки?

3) Сколько простых карандашей взяли из коробки?

Е. В трёх клетках – попугаев поровну. В одной из клеток – 3 попугая. Сколько попугаев в двух других клетках?