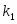
з дисципліни: „Вища математика”

Розділ 6: „Диференціальні рівняння”

на тему:

„Лінійні різницеві рівняння із сталими коефіцієнтами.

Задача Коші.”

1.Лінійні різницеві рівняння із сталими коефіцієнтами.

Основною задачею в диференціальних рівняннях є знаходження їхнього загального розв’язку. Ця задача найповніше вивчена для лінійних рівнянь із сталими коефіцієнтами.

Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами.

Розглянемо лінійне однорідне рівняння другого порядку

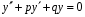1

де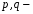дійсні числа.

Ейлер запропонував шукати частинні розв’язки цього рівняння у вигляді 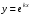, де 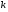- стала(дійсна чи комплексна), яку треба знайти. Підставивши функцію 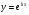в рівняння 1, дістанемо

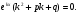
Оскільки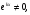 то

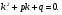2

Отже, якщо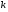 буде коренем рівняння 2, то функція 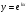буде розв’язком рівняння 1.Квадратне рівняння 2 називається характеристичним рівнянням диференціального рівняння 1.

Позначимо корені характеристичного рівняння через 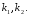можливі три випадки:

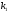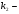І. і дійсні і різні числа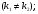

І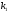І. і 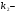комплексні числа);

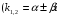ІІІ. і 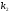- дійсні і рівні числа ;

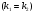Розглянемо кожен випадок окремо.

І.Корені характеристичного рівняння дійсні і різні: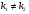 . У цьому випадку частинними розв’язками рівняння 1 є функції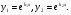

Ці розв’язки лінійно незалежні, тому що при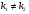

.

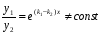Загальний розв’язок рівняння 1 знаходять за формулою .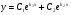

ІІ. Корені характеристичного рівняння комплексно – спряжені:

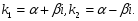
Підставивши значення 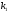та 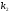у формулу 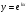,знайдемо розв’язки

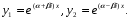
За формулою Ейлера

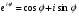
маємо

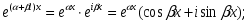
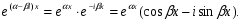
Зауважимо ,що коли функція 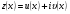є розв’язком рівняння 1, то розв’язками будуть також функції 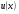та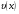. Дійсно, підставивши функції 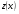в рівняння 1, дістанемо:

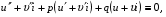
або

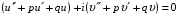
Остання тотожність можлива, коли вирази в дужках дорівнюють нулю. Це означає ,що функції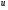та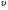 - розв’язки рівняння 1.Згідно з цим зауваженням частинними розв’язками рівняння 1 є функції .

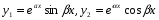Ці розв’язки лінійно незалежні, оскільки

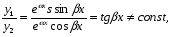
тому загальний розв’язок рівняння 1 запишеться у вигляді

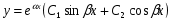3

ІІІ. Корені характеристичного рівняння дійсні і рівні: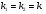 За формулою 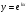дістанемо один з розв’язків :.

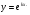Другий розв’язок шукатимемо у вигляді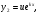 де 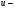невідома функція від 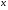. знайшовши 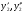та підставивши їх у рівняння 1 дістанемо:

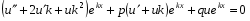
або

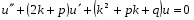
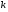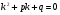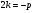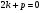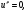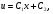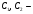Оскільки- корінь рівняння 2, тоі за теоремою Вієта, тому і звідки де довільні сталі. Поклавши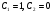(нас цікавить розв’язок 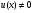), знайдемо другий частинний розв’язок рівняння 1:

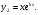
Розв’язки 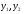- лінійно незалежні, тому загальний розв’язок рівняння 1 має вигляд:

.

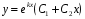Приклад 1:

Розв’язати рівняння:.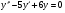

Розв’язання :

Складемо характеристичне рівняння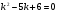 і знайдемо його корені 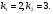за формулою 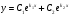шуканий розв’язок має вигляд:

.

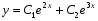Приклад 2:

Розв’язати рівняння:

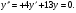
Розв’язання:

Характеристичне рівняння 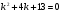має комплексні корені 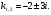Загальний розв’язок дістанемо за формулою 3:

.

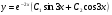Неоднорідні диференціальні рівняння із сталими коефіцієнтами. Рівняння із спеціальною правою частиною.

Розглянемо неоднорідне диференціальне рівняння

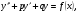4

де 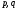- задані дійсні числа, 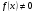- задана функція неперервна на деякому проміжку .

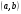Загальний розв’язок такого рівняння являє собою суму частинного

розв’язку рівняння 4 і загального розв’язку відповідного однорідного рівняння. Розглянемо питання про знаходження частинного розв’язку неоднорідного рівняння.

Насамперед слід зазначити , що частинний розв’язок диференціального неоднорідного рівняння 4 можна знайти в квадратурах методом варіації довільних сталих. Проте для рівнянь із спеціальною правою частиною розв’язок можна знайти значно простіше, не вдаючись до операції інтегрування.

Розглянемо деякі з таких рівнянь.

І. Нехай права частина в рівнянні 4 має вигляд

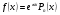, 5

де 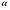- дійсне число, 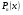- многочлен степеня .

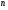Можливі такі випадки:

а) число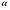 не є коренем характеристичного рівняння

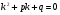6 Тоді диференціальне рівняння 4 має частинний розв’язок виду

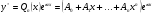, 7 де 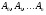- невизначені коефіцієнти.

Справді, підставляючи функцію 7 в рівняння 4, після скорочення на 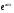дістанемо

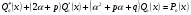8 де 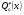- многочлен степеня 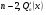- многочлен степеня 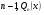і 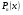- многочлени степеня 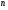.Таким чином зліва і справа в тотожності 8 стоять многочлени степеня 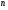.Прирівнюючи коефіцієнти при однакових степенях 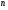, дістанемо систему 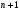лінійних алгебраїчних рівнянь, з якої визначимо 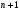невідомих коефіцієнтів 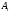многочлена .

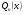Не зупиняючись далі на доведеннях, вкажемо форму, в якій потрібно шукати частинний розв’язок рівняння 4 , залежно від виду правої частини 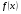цього рівняння;

б) якщо число 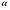збігається з одним коренем характеристичного рівняння 6, тобто є простим коренем цього рівняння, то частинний розв’язок рівняння 4 треба шукати у вигляді

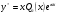; 9

в) якщо число 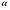є двократним коренем рівняння 6 , то частинний розв’язок рівняння 4 шукають у вигляді

.

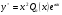Об’єднаємо випадки а)-в): якщо права частина рівняння 4 має вигляд 5, то частинний розв’язок цього рівняння треба шукати у вигляді

,

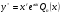де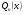- многочлен з невизначеними коефіцієнтами того самого степеня, що й многочлен 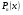,а - число коренів характеристичного рівняння, які дорівнюють 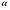. Якщо 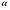не є коренем характеристичного рівняння, то приймаємо .

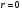ІІ. Нехай права частина в рівнянні 4 має вигляд

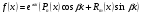, 9.1

де 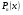- многочлен степеня 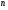, 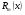- многочлен степеня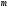; 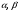- дійсні числа.

Частинний розв’язок рівняння 4 треба шукати у вигляді

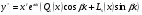, 9.2

де 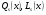многочлени степеня 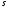з невизначеними коефіцієнтами; 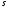- найвищий степінь многочленів 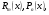тобто 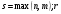- число коренів характеристичного рівняння, які дорівнюють .

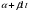Зокрема, якщо права частина рівняння 4 має вигляд

,

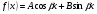де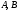- відомі дійсні числа, то частинний розв’язок цього рівняння треба шукати у вигляді

,

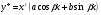де 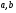- невідомі коефіцієнти; - число коренів характеристичного рівняння 6 , які дорівнюють .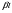

Приклад:

Розв’язати рівняння.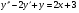

Характеристичне рівняння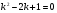 має корені 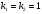, тому загальний розв’язок однорідного рівняння має вигляд 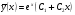.Оскільки правою частиною даного рівняння є функція виду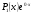,причому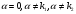, то за формулою 7 частинний розв’язок шукаємо у вигляді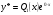,тобто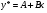, де А і В - знайшовши похідні 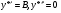і підставивши їх у рівняння дістанемо

.

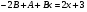Прирівнюючи коефіцієнти при однакових степенях, дістаємо систему рівнянь

,

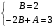звідки 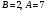.Отже частинний розв’язок даного рівняння має вигляд

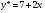, тому

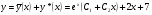
шуканий загальний розв’язок.

Лінійні диференціальні рівняння 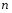-го порядку.

Застосуємо методи знаходження розв’язків диференціальних рівнянь другого порядку до рівнянь вищих порядків.

Нехай маємо лінійне диференціальне рівняння n-го порядку

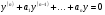, 10 де 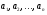- сталі дійсні числа.

Характеристичним для рівняння 10 називається алгебраїчне рівняння n-го степеня виду

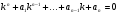11

де 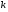- невідоме дійсне чи комплексне число.

Рівняння 11 має n коренів. Позначимо ці корені через .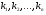

Теорема: Кожному простому кореню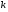рівняння 11 відповідає частинний розв’язок 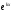рівняння 10, а кожному кореню 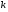кратності 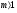відповідає ь частинних розв’язків виду .

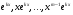Кожній парі 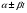простих комплексно спряжених коренів рівняння 11 відповідає два частинних розв’язки 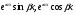рівняння 10 , а кожній парі 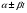комплексно-спряжених коренів кратності 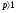відповідає 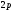частинних розв’язків виду

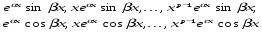
Загальна сума кратностей всіх коренів рівняння 11 дорівнює 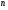, тому кількість всіх частинних розв’язків рівняння 10 , складених згідно з цією теоремою, дорівнює 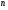.тобто збігається з порядком рівняння 10 . Позначимо ці частинні розв’язки через 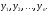Можна показати, що знайдені частинні розв’язки є лінійно незалежними. І загальний розв’язок рівняння 10 знаходиться за формулою

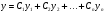. 12

Нехай задано неоднорідне рівняння 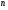-го порядку

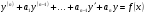13 де 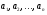- сталі дійсні числа, 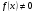- неперервна на деякому проміжку функція.

Як і для рівнянь другого порядку, загальним розв’язком рівняння 13 є функція

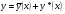де 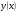- загальний розв’язок відповідного однорідного рівняння 10, а 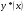- частинний розв’язок рівняння 13.

Побудову загального розв’язку 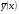рівняння10 з’ясовано. Проаналізуємо знаходження частинного розв’язку 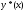. Якщо права частина 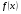рівняння 13 є функція спеціального виду 9.1, то частинний розв’язок цього рівняння треба шукати за формулою 9.2. якщо права частина 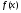не є функцією виду 9.1, то для знаходження 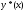застосовують метод варіації довільних сталих. Стосовно рівняння 13 суть цього методу така.

Нехай функція 12 є загальним розв’язком відповідного однорідного рівняння 10. знаходимо частинний розв’язок рівняння 13 за тією ж формулою 12, вважаючи. Що величини 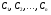- функції від 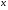, тобто покладемо

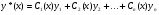, 14 де 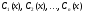- невідомі функції.

Складемо систему рівнянь

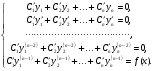
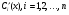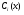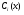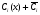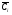розв’язуючи цю систему. Знаходимо похідні , а потім інтегруванням і самі функції . Якщо взяти всі сталі інтегрування рівними нулю і підставити функції в рівність 14 то матимемо частинний розв’язок рівняння 13; якщо у рівність 14 підставити функції, де - довільні сталі. То відразу отримаємо загальний розв’язок.

Приклад:

Розв’язати рівняння .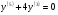

Характеристичне рівняння 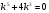має корені 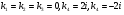. Згідно з теоремою маємо частинні розв’язки: 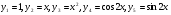. Загальний розв’язок даного рівняння знаходимо за формулою 12:

.

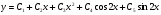ПЛАН

1. Лінійні різницеві рівняння із сталими коефіцієнтами.

Контрольні питання:

1.Що називається лінійним однорідним диференціальним рівнянням другого порядку із сталими коефіцієнтами ?

2.Яке рівняння називається характеристичним? Як його знаходять?

3. Який вигляд має розв’язок лінійного однорідного рівняння другого порядку із сталими коефіцієнтами , якщо корені характеристичного рівняння дійсні і різні?

4. Який вигляд має розв’язок лінійного однорідного рівняння другого порядку із сталими коефіцієнтами , якщо корені характеристичного рівняння дійсні рівні?

5. Який вигляд має розв’язок лінійного однорідного рівняння другого порядку із сталими коефіцієнтами , якщо корені характеристичного рівняння комплексні?

6. Для яких диференціальних рівнянь застосовується метод підбору?

7.Як знайти загальний розв'язок лінійного однорідного рівняння 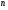-го порядку із сталими коефіцієнтами?

8. як знайти частинний і загальний розв’язки неоднорідного диференціального рівняння 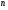-го порядку із сталими коефіцієнтами?

Література:

Барковський В.В., Барковська Н.В. Вища математика для економісті . -.,2002.

Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник. - К.: А.С.К., 2001.