Математический анализ
 1.Счетные и несчетные множества. Счетность множества рациональных чисел.
1.Счетные и несчетные множества. Счетность множества рациональных чисел.
Множество - совокупность некоторых объектов
Элементы множества - объекты составляющие множество
Числовые множества - множества элементами которых являются числа.
Задать множество значит указать все его элементы:
1 Способ: А={а: Р(а)} эти записи Читать- множество тех а таких что...
A={а-Р(а)} равноценны
Р(а) - предикат = высказывание об элементе, бывает ложно или истинно по отношению к кокретному элементу. Множество А состоит из тех а для которых предикат истина.
2 Способ: Конструирование из других множеств:
AB = {c: cA cB}, AB = {c: cA cB}, A\ B = {c: cA сB}
U - универсальное множество (фиксированное)
UA; U \ A = A’ = cA (A’ - дополнение множества A)
Свойства:
1. A(BC)=(AB)C - ассоциативность; AB=BA - коммутативность; A=A; AU=U
2. A (BC)=(AB)(AC) & A (BC)=(AB)(AC) - дистрибутивность; А=А
A” =A - закон исключающий третьего (AB)’=A’B’; (AB)’=A’B’; AA’=
Иллюстрация свойств: Диаграммы Эйлера-Венна.
"=>" c(AB)’ => cAB => cA & cB => c A’ & cB’ => cA’B’
"<=" cA’B’ => cA’ & cB’ => cA & cB => cAB => cAB)’
Отображение множеств:
f:Aна множестве А задано отображение f со значением множества B
aA; b=> b - образ элемента а при отображении f; a - прообраз элемента b при отображении f
Так как для каждого элемента из А ставится в соответствие элемент из В, значит А - область определения (Dom f=А), а область значенийB (Im f B)
Для отображения задают: 1) способ 2) Dom 3) Im
Отображение f инъективно если f(x)=f(x’) => x=x’(разные переходят в разные)
Отображение f сурьективно если Im f =B(каждый переходит в каждый)
Если же отображение инъективно+сурьективно, то множества равномощны(содержат одинаковое кол-во элементов), а отображение биективно - взаимооднозначно.
Счетные множества - множества равномощные множеству натуральных чисел (N)
Теорема: Множество Q счетно.
Докозательство: Q=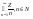
Лемма 1: nN Z/n - счетно.
Каждому элементу из N надо взаимноднозначно сопоставить элемент Z/n:
10/n 5-2/n
2/n 63/n
3-1/n 7-3/n
42/n ...
Лемма 2: Объединение счетного или конечного(не более чем счетного) числа счетных множеств - счетно.
А1={а11, а12, а13,...}
А2={а21, а22, а23,...}
А3={а31, а32, а33,...}
...
Применяем диагональную нумерацию (а11 - 1; а21 - 2; а12 - 3; а31 - 4; а22 - 5...) и таким образом взаимнооднозначно сопоставляем каждому элементу из таблицы его номер, значит объединение счетного или конечного числа счетных множеств - счетно.
Часть может быть равномощна целому: (-1,1) равномощен R (через полуокружность и лучи)
Из Леммы1 и Леммы 2 получаем: Множество рациональных чисел счетно
2. Определение действительного числа бесконечной десятичной дробью. Плотность Q в R.
Действительные числа - множество чисел вида [a0],а1 a2 а3... где а0Z а1,а2,а3,...{0,1,...,9}
Действительное число представляется в виде суммы целой и дробной части:
[ао],а1 а2 а3...ак (0) = ао + а1/10 + а2/100 + ... +ак/10k = [ао],а1 а2 а3...а’к (9), где а’к=ак-1
х=[хо],х1 х2 х3...хк...
у=[уо],у1 у2 у3...ук...
х’к - катое приближение икса с недостатком = [хо],х1 х2 х3...хк
у”к - катое приближение игрека с избытком = [уо],у1 у2 у3...ук + 1/10k
х’к+1 > х’к (х’к - монотонно растет)
у”к+1 у”k (у”k - не возрастает), т.к. у”к=[уо],у1 у2 у3...ук + 1/10к
у”к+1 = [уо],у1 у2 у3...ук ук+1 + 1/10к+1
у”к - у”к+1 = 1/10к - ук+1 + 1/10к+1 0
10 - ук+1 - 1 / 10к+1 0
9 ук+1
Определение: 1) х > у <=> к: х’к > у”к
2) х = у <=> х’к не> у”к & у”к не> х’к
По определению получаем, что [1],(0)=[0],(9)
Свойства: 1)х, у либо х<у, либо х>у, либо х=у
2) х>у & у>z => х>z
3) х не> х
Док-во (2): х>у у>z
х’к>у”к у’m>z”m
n=max{k;m}
х’nх’к>у”ку”n у’n у’m>z”mz”n
у”n>у’n => х’n>z”n
Определение: Если АR и х,уR аА: х<а<у, то А плотно в R
Теорема: Q плотно в R.
Доказательство: х > у х’к > у”к х х’к у”к у
х х’к / 2 + х’к / 2 > х’к / 2 + у”к / 2 > у”к / 2 + у”к / 2 > у
Видим: х > х’к / 2 + у”к / 2 > у, где (х’к / 2 + у”к / 2)Q
3.Несчетность множества действительных чисел.
Теорема: R несчетно.
Доказательство от противного:
1х1=[х1], х11 х12 х13... |
2х2=[х2], х21 х22 х23... | Пусть здесь нет девяток в периоде
3х3=[х3], х31 х32 х33... |
... | (*)
кхк=[хк ], хк1 хк2 хк3... |
... |
Найдем число которого нет в таблице:
с=[с], с1 с2 с3...
[с][х1] => сх1
с1 {9;х21} => сх2
с2 {9;х32} => сх3
...
ск {9;хк+1к} => схк
Таким образом С - число которое отсутствует в таблице (*)
5.Теорема Дедекинда о полноте R
Пусть 1) 0АR; 2) aA, b: а
Замечания: 1) для Q и I не выполняется (между двумя иррациональными всегда одно рациональное следует из теоремы о плотности Q в R)
2) А называют нижним множеством сечения (нижний класс), В называют верхним множеством сечения (верхний класс)
Доказательство:
aA, b: а A ограничено сверху => SupA=m => b: bm => B ограничено снизу => InfB=n, mn
Докажем, что m = n:
Пусть m
следует, что m=n если обозначим m=n через c, то получим асb
Докажем, что с единственное(от противного):
Пусть с’с,с’>с (с’<с), так как c=n=InfB=m=SupA=>по опр-нию. с’>с (с’<с) найдется такое b(a), что b
8.Лемма о зажатой последовательности (Лемма о двух милиционерах)
Если n0:n>n0 xNyNzN и Lim xN=x, Lim zN=z, причем x=z, то Lim yN=y => x=y=z.
Доказательство: n>n0 xNyNzN
Возьмем произвольно Е>0, тогда n’: n>n’ xN(х-Е,х+Е) & n”: n>n” zN(х-Е,х+Е) => n>max{n0,n’,n”} yN(x-E,x+E)
4. Верхние и нижние грани числовых множеств.
Определение: АR mR, m - верхняя (нижняя) грань А, если аА аm (аm).
Определение: Множество A ограничено сверху (снизу), если существует такое m, что аА, выполняется аm (аm).
Определение: SupA=m, если 1) m - верхняя грань A
2) m’: m’
InfA = n, если 1) n - нижняя грань A
2) n’: n’>n => n’ не нижняя грань A
Определение: SupA=m называется число, такое что: 1) aA am
2) >0 aA, такое, что aa-
InfA = nназывается число, такое что: 1) 1) aA an
2) >0 aA, такое, что aEa+
Теорема: Любое, непустое ограниченное сверху множество АR, имееет точную верхнюю грань, причем единственную.
Доказательство:
Построим на числовой прямой число m и докажем что это точная верхняя грань А.
[m]=max{[a]:aA} [[m],[m]+1]A=>[m]+1 - верхняя грань A
Отрезок [[m],[m]+1] - разбиваем на 10 частей
m1=max[10*{a-[m]:aA}]
m2=max[100*{a-[m],m1:aA}]
...
mк=max[10K*{a-[m],m1...mK-1:aA}]
[[m],m1...mK, [m],m1...mK + 1/10K]A=>[m],m1...mK + 1/10K - верхняя грань A
Докажем, что m=[m],m1...mK - точная верхняя грань и что она единственная:
к: [m’K,m”K)Aк аА: а
Единственность(от противного):
аА, пусть а>m”K => к: а’K>m”K => аа’K>m”K - это противоречит ограниченности => am
Точная верхняя грань:
Пусть l
Теорема: Любое, непустое ограниченное снизу множество АR, имееет точную нижнюю грань, причем единственную.
Рассмотрим множество B{-а: аА}, оно ограничено сверху и не пусто => -SupB=InfA
6.Бесконечно малые и бесконечно большие последовательности. Их свойства.
Определение: Последовательность аN называется бесконечно малой (бм) если ее предел равен нулю (Е>0 n0: n>n0 |аN|<Е)
Теорема: Сумма (разность) бм последовательностей является бм последовательностью.
Доказательство: Пусть Lim aN=Lim bN=0, cN=aN+bN, dN=aN-bN. Так как вне любой эпсилон-окрестности точки 0 (в частности окрестности Е/2) лежит конечное число членов последовательности aN, т.е. n’: n>n’: |aN|<Е/2. Аналогично n”: n>n”: |bN|<Е/2. При n>max{n’,n”} выполнены оба неравен ства |aN|<Е/2 & |bN|<Е/2 => при любом n> max{n’,n”} имеем: |cN|=|aN+bN||aN|+|bN|
Теорема: Произведение бм и ограниченной последовательности - бм последовательность.
Доказательство: Пусть aN - бм посл-ть, bN - ограниченная посл-ть zN=aN*bN.
Т.к. bN - ограниченная посл-ть, значит такое с: |bN|с0
Т.к. aN - бм посл-ть, значит вне любой Е-окрестности точки 0 (в частности Е/с)лежит конечное число членов посл-ти aN, т.е. n0: n>n0 |aN|<Е/с.Таким образом n>n0: |zN|=|aN*bN|=|aN|*|bN|<Е/с * с=Е
Следствие: произведение бм посл-тей - тоже бм посл-ть
Теорема: Пусть aN - бм. Еслиn’: n>n’ последовательностьть |bN|aN => bN - бм
Доказательство: aN - бм => n”: n>n”: |aN|<Е. Для n>=max{n’,n”} |bN||aN|<Е
Определение: Последовательность аN называется бесконечно большой (бб) если Е>0 n0: n>n0 |аN|>Е)
Теорема: Если aN - бм, то 1/aN - бб последовательностьть, обратное тоже верно.
Доказательство:
"=>" aN-бм=>вне любой эпсилон-окрестности точки 0 (в частности 1/Е) находится конечное число членов посл-ти, т.е. n0: n>n0 |aN|<1/E =>1/|aN|>Е.
"<=" 1/|aN| - бб последовательность => Е>0 n0: n>n0 1/|aN|>1/Е => |aN|<Е
Теорема: Пусть aN - бб. Если n’: n>n’ последовательность bN|aN| => bN - бб.
Доказательство: aN - бб => n”: n>n” |aN|>Е. Для n>max{n’,n”} bN|aN|>Е
7.Арифметика пределов
Предложение: Число а является пределом последовательности aN если разность aN-a является бм (обратное тоже верно)
Докозательство: Т.к. Lim aN=a, то |aN-a|<Е. Пусть N=aN-a. |N|=|aN-a|<Е
Обратное: Пусть N=aN-a, т.к. N - бм => |N|Е. |N|=|aN-a|<Е
Теорема: Если Lim xN=x, Lim yN=y, то:
Lim (xN+yN) и Lim (xN+yN)=х+у
Lim (xN*yN) и Lim (xN*yN)=х*у
n yN0 & y0 => Lim (xN/yN) и Lim(xN/yN)=х/у
Доказательство:
Пусть xN=х+N, N - бм; yN=у+N, N - бм
1) (xN+yN)-(х+у)=N+N (По теореме о сумме бм: N+N - бм => (xN+yn)-(х+у)-бм, дальше по предложению)
2) xN*yN - х*у = х*N+у*N+N*N (По теоремам о сумме бм посл-тей и * бм посл-тей на огр. посл-ти получаем: xN*yN - х*у - бм, дальше по предл-нию)
3) xN/yN - х/у = (у*N-х*N) / (у*(у+N))= (у*N-х*N) * 1/у * 1/уN доказательство сводится к доказательству утверждения: если уn - сходящаяся не к 0 посл-ть, то 1/уN тоже сходящаяся последовательность: Lim уN=y => по определению предела получаем n0: n>n0 |уn-у|<у/2 (Е=y/2), что равносильно неравенству: у-у/2<уN<у/2+у, откуда получаем: |уN|уN>у/2.|уN|>у/2=>1/|уN|<2/у => n: 1/|уN|max{2/у, 1/у1, 1/у2,...1/уno}
Теорема: Если хN сходится к х, yN сходится к у и n0: n>n0 последовательность хNуN, то ху
Доказательство(от противного): Пусть х>у. Из опр. предела E>0 (в частности Е<(у-х)/2): n’: n>n’ |xN-x|
(х-Е,х+Е)(у-Е,у+Е)=. И т.к мы предположили, что х>у, то n>max{n’,n”}: хN>уN - противоречие с условием => ху.
5. Определение предела последовательности и его единственность.
Определение: Пусть даны два множества Х и У. Если каждому элементу хХ сопоставлен по определенному правилу некоторый элемент уУ, то говорят, что на множестве Х определена функция f и пишут f:ХУ или х (f(х)| хХ).
Определение: Последовательность-это ф-ция определенная на мн-ве N, со значениями во мн-ве R f:NR. Значение такой ф-ции в (.) nN обозначают аN.
Способы задания:
1) Аналитический: Формула общего члена
2) Рекуррентный: (возвратная) формула: Любой член последовательности начиная с некоторого выражаетс через предидущие. При этом способе задани обычно указывают первый член (или нсколько начальных членов) и формулу, позволющкю определить любой член последовательности через предидущие. Пример: а1=а; аN+1=аN + а
3) Словесный: задание последовательности описанием: Пример: аN = n-ый десятичный знак числа Пи
Определение: Число а называется пределом последовательности аN, если n0: n>n0 выполняется неравенство |аN-a|<. Обозначение Lim aN=a.
Если не существует числа а, являющегося пределом посл-ти, то говорят что последовательность расходится, если существует, то сходится (к числу а).
Геометрически существование предела последовательности означает, что любой интервал вида (а-,а+), называемый эпсилон-окрестностью точки а, содержит все члены последовательности аN начиная с некоторого номера, или что то же самое, вне любой эпсилон-окрестности точки а находится ко нечное число членов последовательности аN.
Определение: Число а назывется пределом посл-ти аN если вне всякой окрестности точки а содержится конечное число членов последова тельности.
Теорема: Сходящаяся последовательность имеет только один предел.
Доказательство(от противного):
Пусть последовательность аN имеет предел а и предел с, причем ас. Выберем такой эпсилон, чтобы пересечение эпсилон-окрестностей точек а и с бы ло пусто. Очевидно достаточно взять эпсилон меньше |а-с|/2. Вне окрестности точки а содержится конечное число членов последовательности => в ок рестности точки с содержится конечное число членов последовательности - противоречие с условием того, что с - предел последовательности.
Теорема: Сходящаяся последовательность ограничена.
Доказательство:
Пусть последовательность аN сходится к числу а. Возьмем какое-либо эпсилон, вне эпсилон-окрестности точки а лежит конечное число членов последо вательности, значит всегда можно раздвинуть окрестность так, чтобы все члены последовательности в нее попали, а это и означает что последователь ность ограничена.
Замечания: 1) Обратное не верно (аn=(-1)N, ограничена но не сходится)
2) Если существует предел последовательности аN, то при отбрасывании или добавлении конечного числа членов предел не меняется.
Порядковые свойства пределов:
Теорема о предельном переходе: Если Lim xN=x, Lim yN=y, n0: n>n0 хNyN, тогда xy
Доказательство(от противного):
Пусть х>у => по определению предела n0’: n>n0’ |хN-х|
Теорема: Если n0:n>n0 aNbNcN и Lim aN=a, Lim cN=c, причем a=c, то Lim bN=b => a=b=c.
Доказательство: Возьмем произвольно Е>0, тогда n’: n>n’ => cN<(a+E) & n”: n>n” => (a-E)
9. Предел монотонной последовательности
Определение: Последовательность называется монотонно возрастающей (убывающей) если n1>n2 (n1
Замечание: Если xN1 строго больше (меньше) xN2, тогда посл-ть называется строго монотонно возрастающая (убывающая) в случае нестрогости неравенства последовательность называется нестрого возрастающей (убывающей).
Теорема: Всякая ограниченная монотонная последовательность сходится.
Доказательство: Пусть хN ограниченная монотонно возрастающая последовательность. Х={xN: nN}
По теореме о существовании точной верхней грани у ограниченного множества имеем: SupX=x, Е>0 xE: (х-Е)<хE => n0 xNo>(х-E). Из монотон ности имеем: n>n0 xNxNo>(x-E), получили xNx=SupX, значит n>n0 xN(x-E,х]<(x-E,x+E)
10.Лемма о вложенных промежутках
Определение: Пусть а,bR и а
1) Mножество хR: ахb (а<х
2) Mножество хR: ахb) - открытый справа (слева) промежуток
3) Mножество хR: а<х & x
4) Mножество хR: ах & хb - числовой луч
5) Mножество хR - числовая прямая
Определение: Число b и а (если они существуют) называются правым и левым концами отрезка (далее промежутка), и его длина равна b-a
Лемма: Пусть aN монотонно возрастает, bN монотонно убывает, n aNbN и (bN-aN)-бм, тогда ! с: n c[aN,bN] (с[aN,bN])
Доказательство:
aNbNb1 aN монтонно возрастает & aNb1 => Lim aN=a
a1aNbN bN монтонно убывает & a1bN => Lim bN=b
aNa bbN aNbN => ab
Lim (bN-aN)=b-a=0(по условию)=>a=b
Пусть c=a=b, тогда aNcbN
Пусть с не единственное: aNc’bN, с’с
aNcbN=>-bN-c-aN => aN-bNc’-cbN-aN => (По теореме о предельном переходе) => Lim(aN-bN)Lim(c’-c)Lim(bN-aN) => (a-b)Lim(c`-c)b-a) =>
0lim(c`-c)0 => 0(c`-c)0 => c’=c => c - единственное.
Перефразировка Леммы: Пусть имеется бесконечнаz посл-ть вложенных друг в друга промежутков (промежуток 1 вложен в промежуток 2 если все точки промежутка 1 принадлежат промежутку 2: [a1,b1],[a2,b2],...,[an,bn]..., так что каждый последующий содержится в предыдущем, причем длины этих промежутков стремятся к 0 при n lim(bN-aN)=0, тогда концы промежутков aN и bN стремятся к общему пределу с (с разных сторон).
42.Локальный экстремум. Теорема Ферма и ее приложение к нахождению наибольших и наименьших значений.
Определение: Пусть задан промежуток I=(a;b), точка x0a;bТочка x0, называется точкой локалниого min(max), если для всех xa;bвыполняется
f(x0)
Лемма: Пусть функция f(x) имеет конечную производную в точке x0. Если эта производная f‘(x0)>0(f‘(x0)<0), то для значений х, достаточно близких к x0 справа, будет f(x)>f(x0) (f(x)
Доказательство: По определению производной,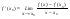 .
.
Если f‘(x0)>0, то найдется такая окрестность (x0-,x0+) точки x0, в которой (при хx0) (f(x)-f(x0))/(x-x0)>0. Пусть x0
Теорема Ферма: Пусть функция f(x) определена в некотором промежутке I=(a;b) и во внутренней точке x0 этого промежутка принимает наибольшее (наименьшее) значение. Если функция f(x) дифференцируема в точке x0, то необходимо f‘(x0)=0.
Доказательство: Пусть для определенности f(x) принимает наибольшее значение в точке x0. Предположение, что f‘(x0)0, приводит к противоречию: либо f‘(x0)>0, и тогда (по лемме) f(x)>f(x0), если x>x0 и достаточно близко к x0, либо f‘(x0)<0, и тогда f(x)>f(x0), если x
Следствие: Если существует наибольшее (наименьшее) значение функции на [a;b] то оно достигается либо на концах промежутка, либо в точках, где производной нет, либо она равна нулю.
43.Теоремы Ролля, Лагранжа, Коши (о среднем значении).
Теорема Ролля
Пусть 1) f(x) определена и непрерывна в замкнутом промежутке [a;b]
2) сущестует конечная производная f’(x), по крайней мере в отткрытом промежутке (a;b)
3) на концах промежутка функция принимает равные значения: f(a)=f(b)
Тогда между a и b найдется такая точка c(a
Доказательство: f(x) непрерывна в замкнутом промежутке [a;b] и потому, по второй теореме Вейерштрасса (Если f(x), определена и непрерывна в замкну том промежутке [a;b], то она достигает в этом промежутке своих точных верхней и нижней границ), принимает в этом промежутке как свое наибольшее значение M, так и свое наименьшее значение m.
Рассмотрим два случая:
1) M=m. Тогда f(x) в промежутке [a;b] сохраняет постоянное значение: неравенство mf(x)M в этом случае x дает f(x)=M => f’(x)=0 во всем промежутке, так что в качестве с можно взять любую точку из (a;b).
2) M>m. По второй теореме Вейерштрасса оба эти значения функцией достигаются, но, так как f(a)=f(b), то хоть одно из них достигается в некоторой точ ке с между a и b. В таком случае из теоремы Ферма (Пусть функция f(x) определена в некотором промежутке I=(a;b) и во внутренней точке x0 этого промежутка принимает наибольшее (наименьшее) значение. Если функция f(x) дифференцируема в точке x0, то необходимо f‘(x0)=0) следует, что произ водная f’(с) в этой точке обращается в нуль.
Теорема Коши:
Пусть 1) f(x) и g(x) непрерывны в замкнутом промежутке [a;b] & g(b)g(a)
2) сущестуют конечные производные f’(x) и g’(x), по крайней мере в отткрытом промежутке (a;b)
3) g’(x)в отткрытом промежутке (a;b)
Тогда между a и b найдется такая точка c(a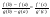
Доказательство: Рассмотрим вспомогательную функцию h(x)=[f(x) - f(a) -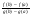 *(g(x) - g(a))]
*(g(x) - g(a))]
Эта функция удовлетворяет всем условиям теоремы Ролля:
1) h(x) непрерывна на [a;b], как комбинация непрерывных функций
2) сущестует конечная производная h’(x) в (a;b), которая равна h’(x)=f’(x) -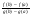 *g’(x)
*g’(x)
3) прямой подстановкой убеждаемся h(a)=h(b)=0
Вследствие этого в промежутке (a;b) существует такая точка с, что h’(x)=0 => f’(c) -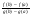 *g’(c) или f’(c) =
*g’(c) или f’(c) =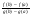 *g’(c).
*g’(c).
Разделив обе части равенства на g’(x) (g’(x)0) получаем требуемое равенство.
Теорема Лагранжа:
Пусть 1) f(x) определена и непрерывна в замкнутом промежутке [a;b]
2) сущестует конечная производная f’(x), по крайней мере в отткрытом промежутке (a;b)
Тогда между a и b найдется такая точка c(a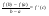
Доказательство: По теореме Коши, полагая g(x)=x, имеем: 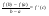
Промежуточное значение с удобно записывать в виде с=а+b-a, где (0;1). Тогда принимая x0=a, (b-a)=h, мы получаем следующее следствие:
Следствие: Пусть f(x) дифференцируема в интервале I=(a;b), x0 x0+hтогда 0;1f(x0+h)-f(x0)=f’(x0+h)*h ([x0;x0+h] h>0, [x0+h;x0] h<0)
11. Подпоследовательности. Теорема Больцано-Вейерштрасса.
Определение: Пусть аN некоторая числовая посл-ть и kN-строго возрастающая посл-ть N чисел. В результате композиции ф-ций naN и nkN получа ем посл-ть aKn-которая наз. подпосл-тью посл-ти aN=>подпосл-сть - это либо сама посл-ть либо исходная посл-ть, из которой выбросили часть членов.
Теорема: Если Lim аN=а, то и Lim аKn=а.
Доказательство: Вне любой Е-окрестности точки а лежит конечное число членов последовательности аn и в частности последовательности.
Доказательство: Пусть для заданного Е нашлось n0: n>n0 |аN-а|<Е, ввиду того что kNсуществует и такое n’, что при всех n>n’ kN>n0 тогда при тех же значениях n будет верно |аKn-а|<Е
Теорема Больцано-Вейерштрасса: Из всякой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство: хN - ограничена => n: ахNb. Поделим промежуток [a,b] пополам, хотя бы в одной его половине содержится бесконечное множество членов посл-ти хN (в противном случае и во всем промежутке содержится конечное число членов посл-ти, что невозможно). Пусть [а1,b1] - та половиа, которая содержит бесконечное число членов посл-ти. Аналогично выделим на промежутке [а1,b1] промежуток [а2,b2] также содержащий бесконечное число членов посл-ти хN. Продолжая процесс до бесконечности на к-том шаге выделим промежуток [аK,bK]-также содержащий содержащий бесконеч ное число членов посл-ти хN. Длина к-того промежутка равна bK-аK = (b-a)/2K, кроме того она стремится к 0 при к и аKаK+1 & bKbK+1. Отсюда по лемме о вложенных промежутках ! с: n аNcbN.
Теперь построим подпоследовательность:
хN1 [а1,b1]
хN2 [а2,b2] n2>n1
. . .
хNK[аK,bK] nK>nK-1
ахNkb. (Lim aK=LimbK=c из леммы о вложенных промежутках)
Отсюда по лемме о зажатой последовательности Lim хNk=c - ч.т.д.
12.Верхний и нижний пределы последовательности.
xN - ограниченная последовательность =>n аNхNbN
хNKх, так как хNK-подпоследовательность => n ахNb =>ахb
х - частичный предел последовательности хN
Пусть М - множество всех частичных пределов.
Множество М ограничено (аМb) => SupM & InfM
Верхним пределом посл-ти xN называют SupMSup{xN}: пишут Lim xN
Нижним предел ом посл-ти xn называют InfMnf{xN}: пишут lim xN
Cуществование нижнего и верхнего пределов вытекает из определения.
Достижимость:
Теорема: Если хN ограничена сверху (снизу), то подпосл-ть хNK: предел которой равен верхнему (нижнему) пределу хN.
Доказательство: Пусть х=SupM=верхний предел хN
х’М: х-1/к<х’ (следует из того что х - SupМ), т.к. х’М => подпоследовательность хNSх’ => Е>0 (в частности Е=1/к) s0: s>s0 =>
х’-1/к<хNS<х’+1/к
х -1/к-1/к<х’-1/к<хNS<х’+1/к<х+1/к (т.к.х-1/к<х’ и х’<х=SupМ)
х-2/к<хNS<х+1/к
Берем к=1: х-2<хNS<х+1, т.е s0: s>s0 это неравенство выполняется берем член посл-ти хNS с номером больше s0 и нумеруем его хN1
k=1: х-2/1<хN1<х+1/1
k=2: х-2/2<хN2<х+1/2 n1
...
k=k: х-2/к<хNK<х+1/к nK-1
При к хNKх
13.Фундаментальные последовательности.
Определение: Последовательность {аN} - называется фундаментальной, если Е>0 n0: n>n0 и любого рN выполнено неравенство |аN+р-аN|<Е. Геометрически это означает что Е>0 n0, такой что расстояние между любыми двумя членами посл-ти, с большими чем n0 номерами, меньше Е.
Критерий Коши сходимости посл-ти: Для того, чтобы данная посл-ть сходилась необходимо и достаточно, чтобы она являлась фундаментальной.
Доказательство:
Необходимость: Пусть Lim xN=x, тогда Е>0 n0: n>n0 |хN-х|<Е/2. n>n0, n’>n0 |хN-хN’|=|хN-х+х-хN’|<|хN-х|+|х-хN’|<Е/2+Е/2<Е
Достаточность: Пусть хN - фундаментальная
1) Докажем что хN ограничена: Е1=1998 n0: |хN-хN’|<Е, n>n0, n’>n0
n>n0 |хN-хN0|<Е1 х N0-1998<хN<х N0+1998 => хN - ограничена
2) По теореме Больцано-Вейерштрасса
подпосл-ть хNKх. Можно выбрать к настолько большим, чтобы |хNK-х|<Е/2 и одновременно nк>n0. Следовательно (из фунд-ти) |хN-хNK|<Е/2 =>
|хNK-х|<Е/2 => х-Е/2<хNK<х+Е/2 => |хN-хNK|<Е/2 => хNK-Е/2<хN<хNK+Е/2 => х-Е<хN<х+Е => |хN-х|<Е
14.Бином Ньютона для натурального показателя.Треугольник Паскаля.
Формула Ньютона для бинома:
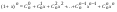 n
n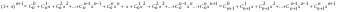

 Разложение Паскаля
Разложение Паскаля
 (Записав коэффициенты в виде пирамиды - получим треугольник Паскаля)
(Записав коэффициенты в виде пирамиды - получим треугольник Паскаля)
...
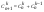
*: 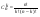 к=0,1,...,n
к=0,1,...,n
Доказательство(по индукции):
1) n=0 - верно (1+х)0=1 =>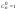 (1+х)0 =
(1+х)0 =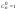
2) Пусть верно для n: докажем что это верно и для n+1:
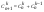 =
= 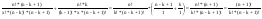 Ч.т.д
Ч.т.д
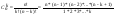
16.Последовательности 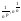 (во всех пределах n)
(во всех пределах n)
1) Lim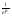 = 0 (p>0)
= 0 (p>0)
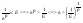 - это означает что, мы нашли такое n0=
- это означает что, мы нашли такое n0=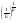 : n>n0 |
: n>n0 |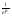 |
|
2) Lim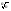 =1
=1
xN=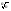 - 1
- 1
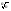 =1+xN
=1+xN
n=(1+xN)n
n=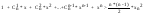
xN2<2/(n-1)
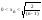 При n
При n 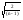 0 => xN0 (Лемма о зажатой последовательности)=>Lim
0 => xN0 (Лемма о зажатой последовательности)=>Lim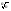 =Lim (1+xN)=1+0=1
=Lim (1+xN)=1+0=1
16.Последовательность (1+1/n)n и ее предел.
xN=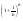 ; yN=
; yN=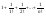 ; zN=yN +
; zN=yN +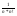
xN монотонно возрастает: докажем:
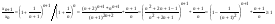
xN=(1+1/n)n=1+ n/1!*1/n + n*(n-1)/2!*1/n2 +... < 1 + 1/1! + 1/2!+...+1/n! = yN => yN
Воспользуемся неравенством Бернулли (1+x)n1+nx, x>-1) (доказывается по индукции):
x=1/n => (1+1/n)n1+n/n=2
Получили: 2 xN<3 => xN - ограничена, учитывая что xN - монотонно возрастает => xN - сходится и ее пределом является число е.
17. Последовательности 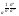 (во всех пределах n)
(во всех пределах n)
1) Lim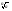 =1, a>0
=1, a>0
a) a1:
xN=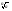 xN+1=
xN+1=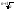
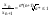 => Lim xN=x
=> Lim xN=x
xN+1=xN *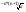
xN=xN+1 *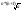
xN=xN+1*xN*(n+1)
Lim xN=Lim (xN+1*xN*(n+1)) => x = x*x => x = 1
б) 0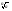
Lim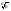 =1 b=1/a =>
=1 b=1/a =>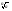 = 1/
= 1/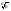 => Lim
=> Lim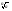 = 1/1 = 1
= 1/1 = 1
2) Lim 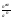 = 0, a>1
= 0, a>1
xN=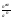 xN+1=
xN+1=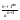
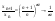 т.к. Lim
т.к. Lim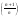 = Lim
= Lim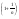 =Lim
=Lim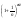 =1
=1
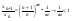 => n0: n>n0 xn+1/xn<1 => СТ x=limxn
=> n0: n>n0 xn+1/xn<1 => СТ x=limxn
xN+1=xN*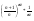
Lim xN+1 = Lim xN*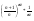 => x = x*1/a => x=0
=> x = x*1/a => x=0
Докажем, что если xN1 => (xN)1:
a) n: xN1 и 0
(xN) [](xN)<(xN)[]+1 => по лемме о зажатой посл-ти, учитывая что Lim (xN)[]=Lim (xN)[]+1=1 (по теореме о Lim произведения) получаем Lim (xN)=1
б) n: 0
yN=1/xN => yn>1 Lim yN=lim1/xN=1/1=1 => (по (а)) Lim (yN) =1 => lim 1/(xN)=1 => Lim (xN) =1
Объединим (а) и (б):
xN1 >0
xN1,xN2,...>1 (1)
xM1,xM2,...<1 (2)
Вне любой окрестности точки 1 лежит конечное число точек (1) и конечное число точек (2) => конечное число точек xN.
в) <0
(xN) =1/(xN) <0 => ->0 => по доказанному для >0 получаем, Lim 1/(xN) = 1 => Lim (xN)
15. Доказательство формулы e=...
yN=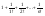 ; zN=yN +
; zN=yN +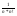
1) yN монотонно растет
2) yN
3) zN-yN0
4) zN монотонно убывает
Доказателство:
zN-zN+1 = yN +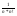 - yN+1 -
- yN+1 -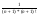 =
= 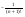 +
+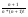 -
-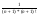 =
=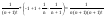
2=y1
e = Lim yN = Lim zN - по лемме о вложенных промежутках имеем: yN<e
Если через обозначить отношение разности e - yN к числу 1/(n*n!), то можно записать e - yN =/(n*n!), заменяя yN его развернутым выражением получаем e = yN + /(n*n!), (0,1)
Число e иррационально:
Доказательство(от противного): Пусть e=m/n, mZ, nN
m/n = e = yN + /(n*n!)
m*(n-1)!= yN*n! + /n, где (m*(n-1)! & yN*n!)Z, (/n)Z => противоречие
23. Определения предела функции по Коши и по Гейне. Их эквивалентность.
Определение по Коши: f(x) сходится к числу А при хх0 если Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е
Определение по Гейне: f(x) сходится к числу А при хх0 если последовательности хNх0, хNх0 f(xN)А
Теорема: Два определения эквивалентны:
Д-во: Для эквивалентности определений достаточно доказать, что из сходимости по Коши следует сходимость по Гейне и из сходимости по Гейне следует сходимость по Коши.
1) (К)=>(Г)
Е>0 >0: 0<|х-х0|< & хDf => |f(x)-А|<Е - определение Коши
хNх0, хNх0, т.к. хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => 0<|xN-x0|< => по определению Коши |f(xN)-А|<Е
2) (Г)=>(К) Воспользуемся законом логики: Если из отрицания B следует отрицание А, то из А следует В:
Таким образом нам надо доказать что из отрицания (К) => отрицание (Г)
Отрицание (К): Е>0: >0 x: 0<|x-x0|< => |f(x)-A|E
Отрицание (Г): хNх0, хNх0: |f(xN)-A|E
хNх0, хNх0 => n0: n>n0 0<|xN-x0|<Е (Е=) => по отрицанию определения Коши |f(xN)-А|Е
Для ф-ции хf(х) определенной на интервале (а,+), определяется предел при хN следующим образом: limf(х) при хN = Limf(1/t) t+0
(если последний существует). Таким же образом определяются Lim f(х) при хN = Lim f(1/t) t0 и хN = lim f(1/t) t0
24. Односторонние пределы. Классификация разрывов. Определение непрерывности.
Lim(х0|h|) при h0 - называется односторонним правым (левым пределом) ф-ции f(x) в точке х0
Теорема: Пусть интервал (x0-,x0+)\{x0} принадлежит области определения ф-ции для некоторго >0. Тогда Lim f(x) в точке х0 существует <=> когда cуществуют правый и левый предел f(x) в точке х0 и они равны между собой.
Необходимость: Пусть предел f(х) существует и равен А => Е>0 >0: -<х-х0< => |f(х)-А|<Е, т.е. такое, что как только х попадает в -окрестность точки x0 сразу f(х) попадает в интервал (f(х)-А,f(х)+А). Если х попадает в интервал (0, x0+) => x попадает в интервал (x0-,x0+) => f(х) попадает в интервал (f(х)-А,f(х)+А) => правый предел существует и он равен А. Если х попадает в интервал (x0-,0) => x попадает в интервал (x0-,x0+) => f(х) попадает в интер вал (f(х)-А,f(х)+А) => левый предел существует и он равен А.
Достаточность: Lim (х0|h|) при h0: Lim(х0+|h|) = Lim(х0-|h|)=А
Е>0 ’ >0: 0<х-х0<’ => |f(х)-А|<Е
Е>0 ” >0: -”<х-х0<0 => |f(х)-А|<Е
Получили Е>0 0<=min{’,”}: - <х-хо< => |f(х)-А|<Е
Определение: Функция f(x) называется непрерывной в точке х0 если при хх0 Lim f(х)=f(х0). Заменяя в определениях предела фнкции по Коши и по Гейне А на f(х0) получаем определения по Коши и по Гейне непрерывности ф-ции f(x) в точке х0. Поскольку в опр-нии по Коши нер-во |f(х)-f(х0)|<Е выполнено и при х=х0 => в определении можно снять ограничение хх0 => получим второе равносильное определение:
Определение 2: Функция f(x) называется непрерывной в точке х0, если Е>0 >0: - <х-хо< => |f(х)-f(а)|<Е
Аналогично сняв ограничение хх0 - получим определение по Гейне:
Определение 3: Функция f(x) называется непрерывной в точке х0, если посл-ти хNх0, f(xN)f(a)
Если при хх0 limf(х)f(х0), то говорят что функция f(x) имеет разрыв в точке х0. Это происходит если:
а) f(х) неопределена в точке х0
б) Предел f(х) в точке х0 не существует
в) f(х) определена в х0 и limf(х) в точке х0 существует но равенство Дшь f(х)=f(а) не выполняется
Различают:
1) точки разрыва I рода, для которых существуют конечные односторонние пределы (либо они неравны друг другу либо равны, но неравны f(х0)
2) точки разрыва II рода - не существует хотя бы один односторонний предел.
Если правый и левый предел в х0 совпадают, то х0 называют устранимой точкой разрыва.
Если хотя бы один из односторонних пределов равен бесконечности, то х0 - точка бесконечного разрыва.
Пусть x0 - точка разрыва, x0 называется изолированной, если в некоторой окрестности этой точки других точек разрыва нет.
Если значение правого (левого) предела в точке х0 совпадает со значением f(x0), то f(x) называется непрерывной справа (слева).
Если предел f(x) справа (слева) в точке х0 не существует, а предел слева (справа) существует и равен значению f(х0), то говорят что функция f(x) имеет в точке х0 разрыв справа (слева). Такие разрывы называют односторонними разрывами f(x) в точке х0.
Функция хf(x) называется непрерывной на множестве Х если она непрерывна в каждой точке х этого множества.
26. Арифметика пределов функций. Порядковые свойства пределов.
Теорема: Все пределы в точке х0: Пусть ф-ции f:ХR и g:ХR (ХR) таковы, что Lim f(x)=F, Lim g(x)=G, тогда
Lim f(x) Lim g(x) = FG
Lim f(x)*Lim g(x) = F*G
Если G0 и g(x)0 Limf (x) / Lim g(x) = F/G
Доказательство:
1) Е>0(в частности Е/2) ’>0: -’<х-х0<’ => |f(х)-F|<Е & ”>0: -”<х-х0<” => |g(х)-G|<Е
Получили Е>0 0<=min{’,”}: -<х-х0< =>-Е/2 - Е/2
2) Пусть посл-ть хNх0 (хNх0, xNX), тогда в силу определения предела по Гейне имеем: при n Lim f(xN)=F & Lim g(xN)=G по теореме об арифметике пределов посл-тей получаем: при n Lim f(xN)*g(xN)=Lim f(xN)*Lim g(xN)= F*G => по определению предела по Гейне при хх0 Lim f(x)*Lim g(x)=F*G
3) Пусть посл-ть хNх0 (хNх0, xNX), тогда в силу определения предела по Гейне имеем: при n Lim f(xN)=F & Lim g(xN)=G по теореме об арифметике пределов посл-тей получаем: при n Lim f(xN)/g(xN)=Lim f(xN)/Lim g(xN)=F/G => по определению предела по Гейне при хх0 Lim f(x)/Lim g(x)=F/G, G0 и g(x)0.
Порядковые свойства пределов:
Теорема: Если хX: f(x)g(x), при хх0 A=Lim f(x), B=Lim g(x), то AB
Доказательство(от противного):
Пусть A>B => из определения предела следует (берем 0<Е<|A-B|/2): ’>0: |х-х0|<’ => |f(x)-A|
Получили, что 0<=min{’;”}: |х-х0|< => |f(x)-A|<|A-B|/2 & |g(х)-B|<|A-B|/2, учитывая что А>В и что (А-Е,А+Е)(В-Е,В+Е)= получаем что для
х(х0-, х0+) f(x)>g(x) - противоречие с условием.
Теорема: Если хX: f(x)g(x)h(x) и при хх0 Lim f(x)=А=Lim h(x), то Lim g(x)=А
Доказательство:
Е>0 ’>0: |х-х0|<’ => A-E
Получили, что 0<=min{’;”}: |х-х0|< => A-E
27. Непрерывность тригонометрических функций. Предел (Sin x)/x при х
1) Sin x:
Lim Sin x = Sin x0 (при хх0)
|Sin x-Sin x0|=2*|Sin((x-x0)/2)|*|Cos((x+x0)/2)| < 2*|(x-x0)/2|=|x-x0| => -|x-x0|
2) Cos x:
Lim Cos x = Cos x0 (при хх0)
Cos x = Sin (П/2 - x) = Sin y; Cos x0 = Sin (П/2 - x0) = Sin y0
|Sin y-Sin y0|=2*|Sin((y-y0)/2)|*|Cos((y+y0)/2)| < 2*|(y-y0)/2|=|y-y0| => -|y-y0|
3) Tg x - непрерывная ф-ция исключая точки х = П/2 +2Пк, кZ
4) Ctg x - непрерывная ф-ция исключая точки х = Пк, кZ
Теорема: Lim (Sin x)/x=1 (при х0), 0
Доказательство:
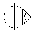
Составляем нер-во для площадей двух треугольников и одного сектора (Sсект=х*R2) откуда и получаем Sinx
28.Теорема о промежуточном значении непрерывной функции.
Определение: Пусть а,bR и а
1) Mножество хR: ахb (а<х
2) Mножество хR: ахb) - открытый справа (слева) промежуток
3) Mножество хR: а<х & x
4) Mножество хR: ах & хb - числовой луч
5) Mножество хR - числовая прямая
Теорема: Пусть f(x) непрерывна на [a,b] и с - произвольное число лежащее между f(а) и f(b), тогда существует х0[a,b]: f(х0)=c.
Доказательство: g(х)=f(х)-с (g(x) - непрерывна). g(а)*g(b)<0
Поделим промежуток [a,b] пополам, если в точке деления g((а+b)/2)=0, то полагая х0=(а+b)/2 видим что теорема доказана (g(х0)=f(х0)-с=0 => f(х0)=с). Пусть в точке деления функция g(x) в ноль не обращается, тогда выбираем из двух полученных промежутков тот, для которого g(а1)*g(b1)<0, делим его пополам если в точке деления функция g(x) обращается в ноль => теорема доказана. Пусть в точке деления функция g(x) в ноль не обращается, тогда выбираем из двух полученных промежутков тот для которого g(а2)*g(b2)<0... продолжая процесс до бесконечности мы либо получим на каком-либо шаге что ф-ция g(x) обращается в ноль, что означает что теорема доказана, либо получим бесконечное число вложенных друг в друга промежутков. Для n-го промежутка [aN,bN] будем иметь: g(aN)<0, g(bN)>0, причем длина его равна bN-aN=(b-a)/2n0 при n. Построенная посл-ть промежутков удов летворяет условию Леммы о вложенных промежутках => точка x0 из промежутка [a,b], для которой Lim aN=Lim bN= x0. Покажем, что x0-удовлетворяет требованию теоремы: g(aN)<0, g(bN)>0 => переходим к пределам: Lim g(aN)0, Lim g(bN)0, используем условие непрерывности: g(x0)0 g(x0)0 => g(x0)=0 => f(х0)-c=0 => f(х0)=c
Следствие: Если функция f(x) непрерывна на промежутке Х, то множество У=f(Х)={f(х):хХ} также является промежутком (Непрерывная ф-ция перево дит промежуток в промежуток.)
Доказательство: Пусть у1,у2У; у1уу2, тогда существуют х1,х2Х: у1=f(х1), у2=f(х2). Применяя теорему к отрезку [х1,х2]Х (если х1<х2) и к отрезку
[х2,х1]Х (если х2<х1) получаем, что у=f(с) при некотором с => У - удовлетворяет определению промежутка.
29. Предел суперпозиции функций. Непрерывность суперпозиции непрерывных функций
Определение: Суперпозицией (композицией) двух функций f и g называется функция f(g(x)) - определенная для всех х принадлежащих области опреде ления ф-ции g таких что значения ф-ции g(x) лежат в области определения ф-ции f.
Теорема: Если Lim g(x)=b (при xa) и f - непрерывна в точке b, то Lim f(g(x))=f(b) (при xa)
Доказательство:
Пусть xN: xNa - произвольная посл-ть из области определения ф-ции хf(g(x)), сходящаяся к а, тогда последовательность yN: yN=g(xN) сходится к b в силу опр. по Гейне. Но тогда Lim f(yN)=f(b) (n) в силу опр. непрерывности ф-ции f по Гейне. Т.о. Lim f(g(xN))=Lim f(yN)=f(b) (n). Заметим что в посл-ти yN - некоторые (и даже все члены) могут оказаться равными b. Тем не менее в силу нашего замечания о снятии ограничения yNb в определении непрерывности по Гейне мы получаем f(yN)f(b)
Следствие: Пусть функция g непрерывна в точке x0, а функция f непрерывна в точке у0=g(x0), тогда ф-ция f(g(x)) непрерывна в точке х0.
30. Обращение непрерывной монотонной функции.
Определение: Функция f обратима на множестве Х если уравнение f(х)=у однозначно разрешимо относительно уf(Х).
Определение: Если функция f обратима на множестве Х. То функция однозначно сопоставляющая каждому уо такое х0 что f(х0)=у0 - называется обратной к функции f.
Теорема: Пусть строго возрастающая (строго убывающая) ф-ция f определена и непрерывна в промежутке Х. Тогда существует обратная функция f’,
определенная в промежутке Y=f(Х), также строго возрастающая (строго убывающая) и непрерывная на Y.
Доказательство: Пусть f строго монотонно возрастает. Из непрерывности по следствию из Теоремы о промежуточном значении следует, что значения непрерывной функции заполняют сплошь некоторый промежуток Y, так что для каждого значения у0 из этого промежутка найдется хоть одно такое значение х0Х, что f(х0)=у0. Из строгой монотонности следует что такое заначение может найтись только одно: если х1> или <х0, то соответственно и f(х1)> или
было х’>х”, тогда из возрастания f следует что у’>у” - противоречие с условием, если х’=х”, то у’=у” - тоже противоречие с условием.
Докажем что f` непрерывна: достаточно доказать, что Lim f`(у)=(у0) при уу0. Пусть f`(у0)=х0. Возьмем произвольно Е>0. Имеем уУ: |f`(у)-f`(у0)|<Е <=> х0-Е
полагая =min{’,”} имеем: как только |у-у0|< => -’<у-у0<” <=> |f`(у)-f`(у0)|<Е
Непрерывность степенной функции с рациональным показателем:
Определение: Степенной функцией с Q показателем называется функция хM/N - где mZ, nN. Очевидно степенная функция явл-ся cуперпозицией непре рывных строго монотонно возрастающих ф-ций хM и х1/M => ф-ция хM/N - непрерывна при х>0. Если х=0, то хM/N = 1, а следовательно непрерывна.
Рассмотрим ф-цию хN, nN: она непрерывна так как равна произведению непрерывных функций у=х.
n=0: хN тождественно равно константе => хN - непрерывна х-N=1/хN, учитывая что:
1) 1/х - непрерывная функция при х0
2) хN (nN) - тоже непрерывная функция
3) х-N=1/хN - суперпозиция ф-ий 1/х и хN при х0
По теореме о непрерывности суперпозиции ф-ций получаем: х-N - непрерывная при х0, т.о. получили что хMmZ - непрерывная ф-ция при х0. При х>0ф-ция хN nN строго монотонно возрастает и ф-ция хNнепрерывна=>функция обратная данной, которая также строго монотонно возрастает (при m>0), очевидно этой функцией будет функция х1/N
Тригонометрические функции на определенных (для каждой) промежутках обратимы и строго монотонны =>имеют непрерывные обратные функции => обратные тригонометрические функции - непрерывны
31. Свойства показательной функции на множестве рациональных чисел.
Определение: Показательная функция на множестве рациональных чисел: Функция вида аX, а>0, а1 xQ.
Свойства: для mZ nN
1) (аM)1/N = (а1/N)M
(аM)1/N=(((а1/N)N)M)1/N = ((а1/N)N*M)1/N = (((а1/N)M)N)1/N = (а1/N)M
2) (аM)1/N=b <=> аM=bN
3) (аM*K)1/N*K=(аM)1/N
(аM*K)1/N*K=b <=> аM*K=bN*K <=> аM=bN <=> (аM)1/N=b
Из свойств для целого показателя вытекают св-ва для рационального если обозначить: aM/N=(аM)1/N=(а1/N)M,a-M/N=1/aM/N, а0=1
Св-ва: x,yQ
1) aX * aY = aX+Y
aX * aY =b; x=m/n, y=-k/n => aM/N * 1/aK/N = b => aM/N = b * aK/N => aM = bN * aK => aM-K = bN => a(M-K)/N = b => aX+Y = b
2) aX/aY = aX-Y
3) (aX)Y=aX*Y
(aX)Y=b; x=m/n, y=k/s => (aM/N)K/S=b => (aM/N)K=bS => (a1/N)M*K=bS => (aM*K)1/N=bS => aM*K=bS*N => a(M*K)/(S*N)=b => aX*Y=b
4) x
z=y-x>0; aY=aZ+X => aY-aX=aZ+X-aX=aX*aZ-aX=aX*(aZ-1) => если aZ>1 при z>0, то aX
z=m/n => aZ=(a1/N)M => a1/N>1 => (a1/N)M>1 => aX*(aZ-1)>1, (a>1 n>0)
5) при x0 aX1 (xR)
Т.к. Lim a1/N=1 (n), очевидно, что и Lim a-1/N=Lim1/a1/N=1 (n). Поэтому Е>0 n0: n>n0 1-E
a-1/N
32.Определение и свойства показательной функции на множестве действительных чисел.
Определение: Показательная функция на множестве действительных чисел: Функция вида аX, а>0, а1 xR.
Свойства: x,yR.
1) aX * aY = aX+Y
xNx, yNy => aXn * aYn = aXn+Yn => Lim aXn * aYn = Lim aXn+Yn => Lim aXn * lim aYn = Lim aXn+Yn => aX * aY = aX+Y
2) aX / aY = aX-Y
3) (aX)Y=aX*Y
xNx, yKy => (aXn)Yk = aXn*Yk => (n) (aX)Yk=aX*Yk =>(k) (aX)Y=aX*Y
4) x
x<x’ x,x’R; xNx x’Nx’ xN,x’NQ => xN<x’N => aXn < aX’n => (n) aXaX’- монотонна
x-x`>q>0 => aX-X’ aQ>1 => aX-X’1 => aX<aX’ - строго монотонна
5) при x n0 aX 1
Т.к. Lim a1/N=1 (n), очевидно, что и Lim a-1/N=Lim1/a1/N=1 (n). Поэтому Е>0 n0: n>n0 1-E
a-1/N
6) aX - непрерывна
Lim aX=1 (n из (5) - это означает непрерывность aX в точке 0 => aX-aXo= aXo(aX-Xo - 1) при хx0 x-x0 n0 => aX-x0 n1 => при хx0 lim(aX - aXo)=
Lim aXo*Lim(aX-Xo - 1) = x0 * 0 = 0 => aX - непрерывна
33.Предел функции (1+x)1/X при x0 и связанные с ним пределы.
1) Lim (1+x)1/X = e при x0
У нас есть Lim (1+1/n)n = e при n
Лемма: Пусть nK nKN Тогда (1+1/nK)Nke
Доказательство:
E>0 k0: n>n0 0
Lim (1+xK)1/Xk при x0+:
1/xK=zK+yK, zKN => 0yK<1 => (1+1/zK+1)Zk<(1+xK)1/Xk < (1+1/zK)Zk+1=(1+1/zK)Zk*(1+1/zK)=>(1+1/zK+1)Zk=(1+1/zK+1)Zk+1)/(1+1/zK+1) => (1+1/zK+1)Zk+1/(1+1/zK+1) < (1+xK)1/Xk < (1+1/zK)Zk*(1+1/zK) kучитывая, что: (1+1/zK)1 (1+1/zK+1)1 => получаем:
eLim (1+xK)1/Xke => Lim (1+xK)1/Xk=e => Lim (1+x)1/X=e при x0+
Lim (1+xK)1/Xk при x0-:
yK=-xK0+ => доказываем аналогично предыдущему => получаем Lim (1+x)1/X=e при x0-
Видим что правый и левый пределы совпадают => Lim (1+x)1/X=e при x0
2) n lim (1+x/n)N = (lim (1+x/n)N/X)X = eX
3) xx R - непрерывна
x=(eLn x)=e*Ln x
непр непр непр непр
xLn x*Ln*Ln x => xe*Ln x
4) x0 Lim (Ln (1+x))/x = Lim Ln (1+x)1/X = Ln e = 1
4’) x0 Lim LogA(1+x)1/X = 1/Ln a
5) x0 Lim (eX-1)/x = {eX-1=t} = Lim t/Ln(1+t) => (4) = 1/1 = 1
5’) x0 Lim (aX-1)/x = Ln a
6) x0 Lim ((1+x)-1)/x = Lim ([e*Ln (1+x) -1/[Ln(1+x)]Ln (1+x)]/x = 11=
34.Теорема Вейрштрасса об ограниченности непрерывной функции на отрезке.
Функция хf(x) называется непрерывной на множестве Х если она непрерывна в каждой точке х этого множества.
Теорема: Функция непрерывная на отрезке [a,b], является ограниченной на этом отрезке (1 теорема Вейрштрасса) и имеет на нем наибольшее и наимень шее значение (2 теорема Вейрштрасса).
Доказательство: Пусть m=Sup{f(x):x[a,b]}. Если f не ограничена сверху на [a,b], то m=, иначе mR. Выберем произвольную возрастающую посл-ть (сN), такую что Lim cN=m. Т.к. nN: cN
Для mR - по теореме о том, что предел произвольной подпосл-ти равен пределу посл-ти получаем cKnm.
Для m=+ - по Лемме о том что всякая подпосл-ть бб посл-ти явл-ся бб посл-тью получаем cKnm. Переходя к пределу в нер-вах cKn
Lim f(xKn)=b n но в силу непрерывности ф-ции f имеем Lim f(xKn)=f() => f()=m - что и означает что функция f ограничена сверху и достигает верхней
граница в точке . Существование точки =Inf{f(x):x[a,b]} доказывается аналогично.
35. Равномерная непрерывность. Ее характеризация в терминах колебаний.
Определение: Е>0 >0: х’,х”: |х’-х”|< => |f(x’)-f(x”)|<Е => функция называется равномерно непрерывной
Отличие от непрерывности состоит в том, что там зависит от Е и от х”, то здесь не зависит от х”.
Определение: Ф-ция f - не равномерно непрерывна, если Е>0 >0: х’,х”: |х’-х”|< => |f(x’)-f(x”)|Е>0
Рассмотрим множество {|f(x’)-f(x”)|:|x’-x”|<, x’,x”I}, IDf.
Верхняя точная граница этого множества обозначаемое Wf() называется колебанием функции f на множестве I вызванное колебаниями аргумента:
1/х - Wf() = +Sin x - Wf() = 1
Таким образом равномерно непрерывную функцию можно определить по другому: Е>0 >0: Wf()Е Lim Wf()=0 0
36.Теорема Кантора о равномерной непрерывности непрерывной функции на отрезке.
Теорема: Если f непрерывна на [a,b], то она равномерно непрерывна на [a,b].
Доказательство(от противного):
Пусть f не равномерно непрерывна на [a,b]=>Е>0 >0 х’,х”: |х’-х”|<=>|f(x’)-f(x”)|Е. Возьмем =1/к, кN хK, х’K[a,b]: |хK-х’K|<1/к |f(xK)-f(x’K)|E
Т.к хK - ограничена => из нее по теореме Больцано-Вейерштрасса можно выделить подпосл-ть xKs сходящуюся к х0. Получаем: |хKs-х’Ks|<1/к
хKs-1/k<х’Ks<хKs-1/k по Лемме о зажатой посл-ти х’Ksх0 kS |f(xKs)-f(x’Ks)|E кS0E - противоречие с условием.
37.Определение производной и дифференциала.
Касательная в точке x0 к функции xf(x): возьмем еще одну точку х соединим x0 и х - получим секущую. Касательной назовем предельное положение секущей при хx0, если это предельное положение существует. Т.к. касательная должна пройти ч/з точку (x0,f(x0) => уравнение этой касательной (если она не вертикальна) имеет вид y=k*(x-x0)+f(x0). Необходимо только опр-ть наклон k касательной. Возьмем произвольное число х0 так, чтобы x0+хХ. Рассмотрим секущую МОМ, МО(x0,f(x0)), М(x0+х,f(x0+х)). Уравнение секущей имеет вид: у=к(х)(х-x0)+f(x0), где k=f((x0+х)-f(x0))/х - наклон секущей. Если существует Lim к(х) при х0, то в качестве искомого наклона k возьмем это предел. Если Lim к(х)=при х0, то перепишем уравнение секу щей в виде x=(1/k(х))*(y-f(x0))+x0 перейдя к пределам при х0, получим x=x0 (Lim x=Lim x0 х0 => x = Lim x0)
Определение: Производным значением функции f в точке х0 называется число f’(х0)=Lim (f(x0+х)-f(x0))/х xx0, если этот предел существует.
Геометрически f’(х0) - это наклон невертикальной касательной в точке (x0,f(x0)). Уравнение касательной y=f’(x0)*(x-x0)+f(x0). Если Lim (f(x0+х)-f(x0))/х= х0, то пишут f`(x0)= касательная в этом случае вертикальна и задается уравнением х=x0. f`(x0)=lim(f(x0+х)-f(x0))/х xx0=>(f(x0+х)-f(x0))/х=f’(x0)+(x), (x)0 при xx0. f(x0+х)-f(x0)=f`(x0)*х+(x)*х учитывая, что x0+х=x и обозначая (x)*х через o(x-x0) получим f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0). Необхо димо заметить, что o(x-x0) уменьшается быстрее чем (x-x0) при xx0 (т.к. o(x-x0)/(x-x0)0 при xx0)
Определение: Ф-ция f называется дифференцируемой в точке x0 если сR: в некоторой окрестности точки x0 f(x)=С(x-x0)+f(x0)+o(x-x0)
Теорема: Функция диффференцируема в точке x0 <=> f’(x0)
Доказательство:
<=: f(x)=f’(x0)*(x-x0)+f(x0)+o(x-x0) => f`(x0)=C
=>: f(x)=C(x-x0)+f(x0)+o(x-x0) => (f(x)-f(x0))/(x-x0)=C+o(x-x0)/(x-x0)=C+(x), (x)0 при xx0.
Переходим к пределу при xx0 => Lim (f(x)-f(x0))/(x-x0)=C+0=C => Слева записано производное значение ф-ции f => по определению C=f`(x0)
Определение: Если функция хf(x) дифференцируема в точке x0, то линейная функция хf’(x0)*х называется дифференциалом функции f в точке x0 и
обозначается df(x0). (диф-ал ф-ции хх обозначают dx). Т.о. df(x0):хf`(x0)*х и dх:хх. Отсюда df(x0)=f’(x0)*dх => df(x0)/dх: хf`(x0)*х/х=f’(x0) при х0. В силу этого пишут также f’(x0)=df(x0)/dх - обозначение Лейбница. График диф-ла получается из графика касательной переносом начала коор динат в точку касания.
Теорема: Если ф-ция f диф-ма в точке x0, то f непрерывна в точке x0.
Докозательство: f(x)=f(x0)+f’(x0)*(x-x0)+o(x-x0)f(x0) при xx0 => f непрерывна в точке x0.
Определение: Нормаль к ф-ции f в точке x0: это прямая перпендикулярная касательной к ф-ции f в точке x0. Учитывая что тангенс угла наклона нормали равен tg(90+угол наклона касательной)= -Ctg(наклона касательной), получаем уравнение нормали: y=-1/f’(x0)*(x-x0)+f(x0)
38. Арифметика диф-цирования. Производные тригонометрических функций.
Теорема: Пусть ф-ции f и g дифференцируемы в точке x0, тогда ф-ции f+g, f*g и f/g (при g(x0)0) дифференцируемы в точке x0 и:
1) (f+g)’(x0)=f’(x0)+g’(x0)
2) (f*g)’(x0)=f’(x0)*g(x0)+f(x0)*g’(x0)
3) (f/g)’(x0)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x0)2
Доказательство:
1) f(x0)=f(x0+x)-f(x0)
g(x0)=g(x0+x)-g(x0)
(f+g)(x0)=f(x0)+g(x0)=f(x0+x)-f(x0)+g(x0+x)-g(x0)
(f+g)(x0)/x=(f(x0+x)-f(x0)+g(x0+x)-g(x0))/x=(f(x0+x)-f(x0))/x+(g(x0+x)-g(x0))/xf’(x0)+g’(x0) при x0
2)(f*g)(x0)=f(x0+x)*g(x0+x)-f(x0)*g(x0)=(f(x0)+f(x0))*(g(x0)+(x0))-f(x0)*g(x0)=g(x0)*f(x0)+f(x0)*g(x0)+f(x0)*g(x0) (f*g)(x0)/x=g(x0)*(f(x0)/x)+f(x0)*(g(x0)/x)+(f(x0)/x)*(g(x0)/x)*xf’(x0)*g(x0)+f(x0)*g’(x0) при x0
3) Ф-ция g - дифференцируема в точке x0 => Ф-ция g - непрерывна в точке x0 => Е>0 (Е=|g(x0)|/2) >0: |x|<=> |g(x0+x)-g(x0)|<|g(x0)|/2.
g(x0)-|g(x0)|/2
Рассмотрим разность (1/g(x0+x)-1/g(x0))/x = -(g(x0+x)-g(x0))/x*g(x0+x)*g(x0) -g’(x0)/g(x0)2 при x0
(f/g)’(x0)=(f*1/g)’(x0) => (2) = f’(x0)*1/g(x0)+f(x0)*(1/g)’(x0)=f`(x0)*1/g(x0)+f(x0)*(-g’(x0)/g(x0)2)=(f’(x0)*g(x0)-f(x0)*g’(x0))/g(x0)2
Теорема: Пусть f=Sin(x), g=Cos(x)
1) Sin’(x0) = Cos (x0)
2) Cos’(x0) = -Sin (x0)
Доказательство:
1)f/x=(Sin(x0+x)-Sin(x0))/x = Sin(x/2)/(x/2) * Cos(x0+x/2) Сos x0 при x0
2) g/x=(Cos(x0+x)-cos(x0))/x=Sin(x/2)/(x/2)*-Sin(x0+x/2) -Sin x0 при x0
Производные Tg и Ctg выводятся непосредственно из производных для Sin и Cos по формулам дифференцирования.
39. Производная суперпозиции.Производные степенной, показательной и логарифмической функции.
Теорема: Пусть функция g диф-ма в точке x0, а ф-ция f диф-ма в точке y0=g(x0), тогда ф-ция h(х)=f(g(х)) диф-ма в точке x0 и h’(x0)=f`(y0)*g’(x0)
Доказательство:
y=y-y0, x=x-x0, f(y0)=f’(y0)*y+o(y), g(xo)=g’(xo)*x+o(x), y=g(x0+x)
h(x0)=f(g(x0+x))-f(g(x0))=f(y)-f(y0)=f’(y0)*y+o(y)=f’(y0)*(g(x0+x)-g(x0))+o(g)==f’(y0)*(g’(x0)*x+o(x))+o(y)= f’(y0)*g’(x0)*x+f’(y0)*o(x)+o(y)
h(x0)/x=f’(y0)*g’(x0)+r, r=f`(y0)*o(x)/x+o(y)/x
r=f`(y0)*o(x)/x+o(y)/x=f`(y0)*((x)*x)/x+(’(x)*y)/x=f’(y0)*(x)+’(x)*y/xf’(y0)*0 + 0*g’(y0) при x0 ((x)0 ’(x)0)
Производная:
1) x=*x-1
Lim (y/x)=lim((x+x)-x)/x = Lim x* ((1+x/x))/x/x. Используя замечательный предел x0 Lim ((1+x)-1)/x=, получим x0
Lim x*Lim((1+x/x))/x/x = x
2) (aX)’=aX*Ln a (xaX)’=(xeX*Ln a)’
xeX*Ln a - композиция функций xеX и xx*Ln a обе непрерывны на R => (xaX)’=(xе X*Ln a)’=(xеX*Ln a)’*(xx*Ln a)’=aX*Ln a
Д-во : (eX)’=eX
Lim(y/x)=Lim(eX+X-eX)/x=LimeX*(eX-1)/x, используя зам-ный предел при x0 Lim(eX-1)/x=1, получим при x0 Lim(y/x)=eX
3) (LogA(x))’=1/x*Ln a
Lim(y/x) = Lim (LogA(x+x) - LogA(x))/x = Lim 1/x*LogA(1+x/x)/x/x, используя замечательный предел при x0 Lim LogA(1+x)/x=1/Ln a, получим
Lim (y/x) = Lim 1/x*Lim LogA(1+x/x)/x/x=1/x*Ln a
40. Производная обратной функции. Производные обратных тригонометрических функций.
Предложение: Если производная обратной функции g для ф-ции f существует в точке y0, то g’(y0)=1/f’(x0), где y0=f(x0)
Доказательство: g(f(x))=x g’(f(x))=1
g’(f(x0))=g’(f(x0))*f’(x0)=1, g’(f(x0))=g(y0)=1/f’(x0)
Теорема: Пусть ф-ция f строго монотонно и непрерывно отображает () в (а,b) тогда обратная ей ф-ция g, которая строго монотонно и непрерывно отображает (а,b) в (). Если f диф-ма в точке x0() и f’(x0)0, то g диф-ма в точке y0=f(x0) и g’(y0)=1/f’(x0)
Доказательство:
Возьмем произвольную последовательность сходящуюся к y0: yNy0, yNy0 => посл-ть xN: xN=g(yN), f(xN)=yN
g(yN)-g(y0)/yN-yO = xN-xO/f(yN)-f(yO) = 1/f(yN)-f(yO)/xN-xO 1/f’(xo) при nполучили при xNxO g(yN)-g(yO)/yN-yO1/f’(xO) => g’(уO)=1/f’(xO)
Производные:
1) xrcsin x по теореме имеем Arcsin’x=1/Sin’y, где Sin y=x при условии, что Sin’y<0, получаем (используя производную синуса): Arcsin’x=1/Cos y, т.к. rcsin: [-1,1][-П/2,П/2] и Cos:[-П/2,П/2][0,1], то Cos y0 и, значит Arcsin’x = 1/Cos y = 1/(1-Sin2y)1/2 = 1/(1-x2)1/2
2) xArccos’x = -1/(1-x2)1/2
3) xArctg’x = 1/1+x2
4) xArcctg’x= -1/1+x2
41.Производные и дифференциалы высших порядков.
Определение: Если ф-ция f диф-ма в некоторой окрестности точки xO, то ф-ция f’(x):xf’(x) в свою очередь может оказаться диф-мой в точке xO или даже в некоторой ее окрестности. Производная ф-ции f’(x) - называется второй производной (или производной порядка 2) ф-ции f в точке xO и обознача ется f”(x). Аналогично определяется третья и четвертая производная и так далее. Для единообразия обозначаем через fN(xO) - производную порядка n функции f в точке xO и при n=0 считаем f0(xO)=f(xO).
Замечание: Cуществование производной порядка n требует того чтобы существовала производная пордка (n-1) уже в некоторой окрестности точки xO (следует из теоремы о связи диф-ти и непрерывности), в таком случае функция xfN-1(x) непрерывна в точке xO, а при n2 все производные порядка не выше (n-2) непрерывны в некоторой окрестности точки xO.
Определение: Дифференциалом ф-ции f порядка n в точке xO называют функцию dхfN(x)*dх и обозначают dNf(x). Таким образом dNf(x):dхfN(x)dxN.
Так как fN(x)dхN:dхfN(x)dxN, то dNf(x)=fN(x)dхN. В силу этого соотношения производную fN(x) обозначают также dNf(x)/dхN
Инвариантность:
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию у=f(g(t)). Если существуют производные у’(х) и х’(t) то cуществует производная у’(t)=у’(х)*х’(t). Если х считать независимой переменной, то диф-ал dy=y’(х)dx. Перейдем к независимой переменной t, учитывая что у’(t)=у’(х)*х’(t): dy=y’(t)dt=y’(x)*х’(t)dt. x’(t)dt=dх => dy=y’(t)dt=у’(х)*х’(t)*dt=у’(x)dх - видим что при переходе к новой независимой переменной форма дифференциала может быть сохранена - это свойство называют инвариантностью формы первого дифференциала.
Пусть функции у=f(х) и х=g(t) таковы, что из них можно составить сложную функцию у=f(g(t)) Если существуют производные у’(х) и х’(t) то существует производная у’(t)=у’(х)*х’(t) и по доказанному ее первый диф-ал по t можно написать в форме dy=y’(х)dх, где dх=x’(t)dt. Вычисляем второй диф-ал по t: d2y=d(y’(x)dx)=dy’(x)dx+y’(x)d(dx). Снова пользуясь инвариантностью первого диф-ла dy’(x)=у”(х2)dx => d2y=у”(х2)dx2x+y’(x)*d2x, в то время как при независимой переменной х второй диф-ал имел вид д2y=у’(х2)*dx2x => неинвариантность формы второго диф-ла.
Формула Лейбница:
f(x)=u(x)*v(x) 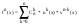
Доказательство по индукции.
1) n=0 верно
2) Предположим для n - верно => докажем для (n+1)
Если для u и v n+1) производные, то можно еще раз продифференцировать по х - получим:
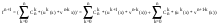
Объединим теперь слагаемые обеих последних сумм, содержащие одинаковые произведения производных функций u и v (сумма порядков производ ных в таком произведении, как легко видеть, равна всегда (n+1)). Произведение u0*vN+1 входит только во вторую сумму с коэффициентом С0N=1. Произведение uN+1*v0 входит только в первую сумму с коэффициентом СNN=1. Все остальные произведения входящие в эти суммы имеют вид uK*vN+1-K. Каждое такое произведение встречается в первой сумме с номером k = i-1, а во второй i=k. Сумма соотв. коэффициентов будет 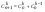 =>
=>
получаем fN+1(x)=u0*vN+1+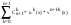 + uN+1*v0=
+ uN+1*v0=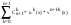
44. Нахождение промежутков постоянства монотонности функции и ее экстремумов.
Теорема: Пусть f(x) непрерывна в замкнутом промежутке [a;b] и диф-ма в открытом промежутке (a;b), если f’(x)=0 в (a;b), то f(x)-const в [a;b].
Докозательство:
Пусть xb, тогда в замкнутом промежутке в [a;x] по теореме Лагранжа имеем: f(x)-f(a)=f’(a+(x-a))(x-a) 0<т.к. по условию f’(x)=0 в (a;b), то f’(a+(x-a))=0 => f(x)=f(a)=Const для все х(a;b).
Теорема: Пусть f(x) непрерывна в замкнутом промежутке [a;b] и диф-ма в открытом промежутке (a;b), тогда:
1) f монотонно возрастает(убывает) в нестрогом смысле в (a;b) <=> f’(x)0(f’(x)0) в (a;b).
2) Если f’(x)>0(f’(x)<0) в (a;b) и f непрерывна в [a;b], то f строго возрастает(убывает) в [a;b].
Доказательство:
1) Пусть f непрерывна на [x’,x”] x’, x”(a;b), тогда по теореме Лагранжа (f(x”)-f(x’))/(x”-x’)=f’(c), с(x’,x”). По условию имеем f’(x)f’(x)в (a;b) => f’(c)f’(c)f(x”)f(x’)( f(x”)f(x’)) => f(x) возрастает(убывает) в нестрогом смысле в (a;b).
2) Используя аналогичные (1) рассуждения, но заменяя неравенства на строгие получим (2).
Следствие: Если xO-критическая точка непрерывной ф-ции f. f’(x) в достаточно малой -окр-ти точки xO имеет разные знаки, то xO-экстремальная точка.
Достаточное условие экстремума: (+)xO(-) => локальный min, (-)xO(+) => локальный max
46. Выпуклые множества Rn. Условие Иенсена. Выпуклые функции.Неравенство Йенсена.
Определение: Множество М выпукло <=> если А,ВМ [А,В]М
[А,В]М => [А,В]={А+t(В-А):t[0,1]} => А(1-t)+tВМ
[А,В]М => А,ВМ; 1=1-t, 2=t => 1+2=1 1,20 => 1А+2ВМ
Рассмотрим точки: А1,А2,...АNМ 1,20 i=1,n):= 1
Докажем что i=1,n):*АI М
Д-во: По индукции:
1) n=1, n=2 - верно
2) Пусть для (n-1) - верно => докажем для n:
а) =1 => приравниваем 1=...==0 => верно
б) <1 *А1 +...+ *А +*А= (1-)((/1-)*А1+...+(/1-)*А) + *А = (1-)*B + *А
BМ - по индуктивному предположению АМ - по условию=>(1-)*B + *АМ Ч.т.д
График Гf = {(x,f(x)):хDf}, Надграфик UPf={(x,y):y>f(x)}
Определение: Функция f выпукла <=> UPf - множество выпукло.
Условие Йенсена: АIМ 0 i=1,n):=1 => i=1,n):*АI М, xI0, f(xI)yI => i=1,n):*АI =xI;*yIf(xI)*yI
Неравенство Йенсена: АIМ 0 =1f(xI)*f(xI)
47.Критерий выпуклости дифференцируемой функции.
Теорема: Пусть f определена в интервале (a;b), тогда следующие условия эквивалентны: 1) f - выпукла в (a;b) ~ 2) x’,xO,x”(a;b) x’
(f(xO)-f(x’))/(xO-x’)(f(x”)-f(xO))/(x”-xO). Геометрический смысл: при сдвиге вправо угловой коэффициент секущей растет.
Доказательство:
“=>” AB: k=(y-f(x’))/(xO-x’)(f(xO)-f(x’))/(xO-x’) => yf(xO); AB: k=(f(x”)-y)/(x”-xO)(f(x”)-f(xO))/(x”-xO) =>yf(xO)
(f(xO)-f(x’))/(xO-x’)(f(x”)-f(xO))/(x”-xO)
“<=”

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ