Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Московский педагогический государственный университет»

математический факультет

кафедра Алгебры.

РЕФЕРАТ

По теме «Некоторые примеры некоммутативных алгебр».

Выполнила:

Студентка

3. группы 6 курса

Браницкая Нина Анатольевна

Научный руководитель:

Ширшова Елена Евгеньевна.

Москва, 2010

Содержание:

Глава 1. Основные понятия и определения 4

Глава 2. Примеры некоммутативных алгебр 3

1. Множество векторов трехмерного векторного пространства над полем 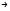3

   1. Свойства векторного произведения 4

   2. Выражение векторного произведения через координаты 4

2. Множество квадратных матриц 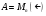над полем 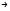5

3. Тело кватернионов К над полем 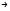5

   1. Основные свойства 6

4. Алгебра Грассмана над полем 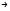9

   1. Следствия 10

5. Список литературы 11

1. Основные понятия и определения.

Определение: Пусть F – поле, V - некоторое множество, на котором заданы следующие операции:

1. операция сложения:

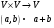
2. операция умножения:

Множество V с заданными на нем операциями сложения и умножения элементов из V на элементы из F называется векторным (линейным) пространством над полем F, если выполняются следующие условия:

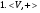- абелева группа;

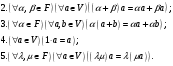
Элементы множества V называются векторами, а элементы поля F – скалярами.

Определение: Векторное пространство А над полем Р называется алгеброй, если выполняются следующие условия:

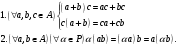
Определение (И.Л. Бухбиндер): Линейное пространство А называется (линейной) алгеброй, если в нем определена бинарная операция умножения элементов, то есть любым двум элементам 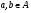сопоставляется единственный элемент, обозначаемый 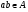: 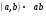, при этом бинарная операция удовлетворяет следующему свойству:

.

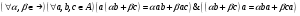Определение: Алгебра 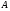называется ассоциативной, если .

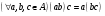Определение: Алгебра 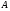называется коммутативной, если .

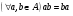Определение: Если в алгебре 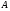существует элемент 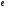, обладающий свойством единицы, то есть 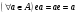, то данная алгебра называется алгеброй с единицей, а элемент 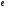- единицей алгебры.

2. Примеры некоммутативных алгебр.

1. Множество векторов трехмерного векторного пространства над полем 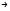, в котором роль бинарной операции умножения играет векторное произведение векторов.

Определение: Векторным произведением вектора 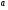на вектор 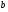называется вектор 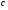, который удовлетворяет следующим условиям:

1. ;

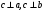2. имеет длину, численно равную площади параллелограмма, построенного на векторах 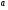и 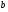, как на сторонах, т.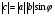е. , где ;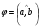

3. векторы 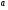, 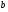и 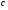образуют правую тройку векторов.

Обозначени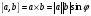е: , где .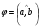

Свойства векторного произведения.

1. При перестановки сомножителей векторное произведение меняет знак, то есть

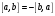
Доказательство: Векторы 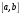и 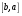коллинеарные, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройк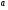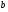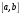и , , и 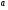, , 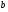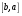противоположной ориентации). Следовательно, .

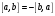2. Векторное произведение обладает ассоциативным законом относительно операции умножения на скаляр, то есть .

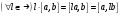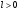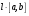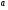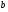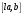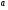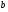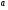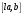Доказательство: Пусть . Вектор перпендикулярен векторам и . Вектор также перпендикулярен векторам и (векторы , лежат в одной плоскости). Значит, векторы и 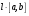коллинеарные, сонаправленые (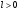), имеют одинаковую длину ()

Поэтому 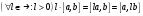. Аналогично доказывается при .

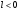3. Два ненулевых вектора 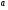и 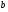коллинеарные тогда и только тогда, когда их векторное произведение равно нулевому вектору, то есть.

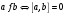Доказательство: 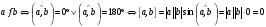. Следовательно, .

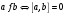В частности, .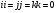

4. Векторное произведение обладает законом дистрибутивности умножения относительно сложения, то есть

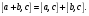
Выражение векторного произведения через координаты.

Таблица векторного произведения векторов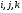

Пусть заданы два вектора 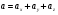и 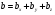, такие, что ,

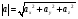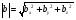
Векторное произведение этих векторов вычисляется по формуле: .

Проверим, является ли векторное пространство 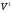линейной алгеброй.

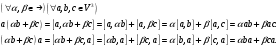
Следовательно, по определению И.Л. Бухбиндера, - алгебра.

Проверим, является ли 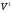ассоциативной алгеброй.

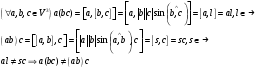
Следовательно, 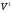не является ассоциативной алгеброй.

Проверим, является ли 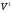коммутативной алгеброй.

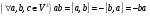, такие образом, .

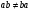Следовательно, 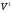не является коммутативной алгеброй.

Замечание: 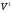является неассоциативной, некоммутативной алгеброй без единицы.

2. Множество квадратных матриц 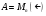над полем 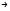, в котором роль бинарной операции умножения играет обычное произведение матриц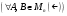

.

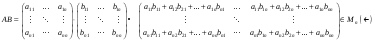Замечание: является некоммутативной, ассоциативной алгеброй с единицей .

3. Тело кватернионов К над полем 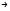. Роль бинарной операции умножения здесь играет обычное умножение кватернионов.

,

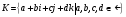где 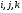- мнимые единицы со следующей таблицей умножения:

Определим бинарные операции сложения и умножения кватернионов:

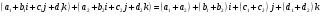
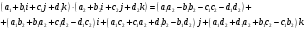
Определение: Кватернион 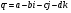называется сопряженным к .

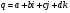Определение: называется модулем кватерниона .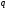

Кватернионы можно определить как комплексные матрицы с обычными матричными произведением и суммой.

Рассмотрим базис: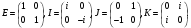

Проверим свойства мнимых единиц кватернионов на данных элементах базиса:

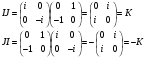
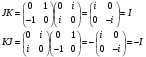
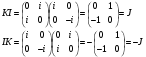
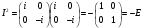
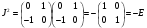
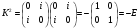
Любой кватернион представим в виде квадратной матрицы:

,

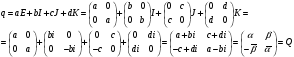здесь 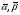- комплексно-сопряженные числа к .

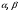Основные свойства.

1. комплексному числу соответствует диагональная матрица;

2. сопряженному кватерниону соответствует сопряженная транспонированная матрица .

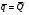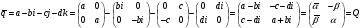
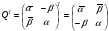
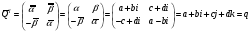
3. квадрат модуля кватерниона равен определителю соответствующей матрицы .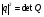

Докажем это свойство: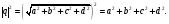

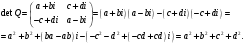
Следовательно, .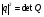

Проверим, является ли 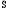алгеброй.

1. 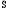- векторное пространство?

а). 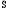- абелева группа?

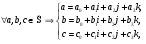
1).

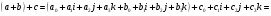
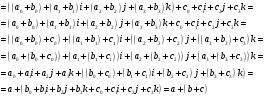
2).

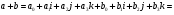
3).

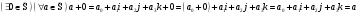
4).

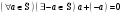
Из 1) - 4) следует, что - абелева группа.

б).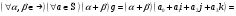

в).

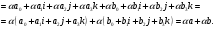
г).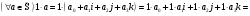

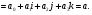
д).

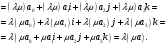
Из а) - д) следует, что 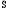- векторное пространство.

2.

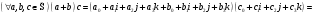
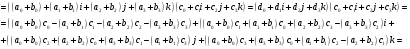
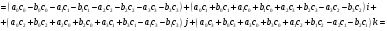
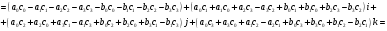
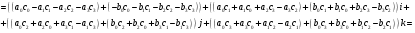
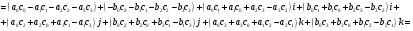
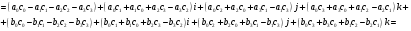
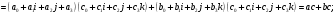
Аналогично проверяется, что

3.

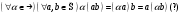
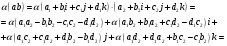
Аналогично проверяется, что .

Из 1-3 следует, что 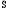- алгебра над полем .

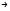Замечание: 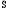- некоммутативная алгебра с единицей Е над полем .

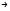4. Алгебра Грассмана над полем .

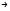Определение: Ассоциативная алгебра с единицей называется алгеброй Грассмана, если в ней существует система линейно-независимых образующих элементов 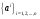, обладающих свойствами:

(a) *свойство антикоммутативности* 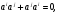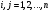(1)

(b) любое другое соотношение между образующими элементами 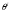является следствием соотношения (1), в частности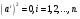

Обозначение: 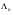- алгебра Грассмана с 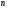образующими элементами.

Выясним, как выглядит произвольный элемент алгебры Грассмана.

Начнем с алгебры 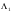. В этом случае имеется только один образующий элемент 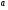, причем 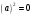, и, поэтому . Следовательно, произвольный элемент алгебры 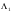есть .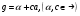

Рассмотрим алгебру 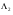, содержащую два образующих элемента 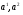, причем 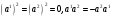. Путем их перемножения можно построить еще один элемент 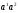. Таким образом, произвольный элемент алгебры 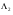выглядит так: .

Обратимся теперь к общему случаю 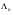. Здесь мы имеем 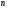образующих элементов 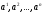. Перемножая эти элементы получим мономы 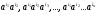, где индексы 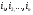принимают значения .

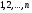Заметим теперь, что любой моном 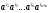, где 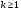, всегда обращается в нуль. Дело в том, что в этом случае среди сомножителей 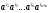какой-нибудь из элементов встретится, по крайней мере, два раза. Используя соотношение (1) переставим сомножители так, чтобы возникло произведение 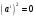.В результате, мы получаем следующие независимые мономы: 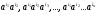. Следовательно, произвольный элемент алгебры 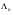имеет вид:

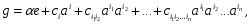(2)

где . По повторяющимся индексам 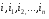подразумевается суммирование от 1 до 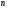в каждом слагаемом.

Следствия.

1. Любой моном, содержащий ровно 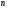сомножителей, равен с точностью до знака произведению .

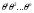2. Рассмотрим соотношение (2),оно представляет собой разложение элемента 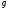некоторого линейного пространства по базису, образованному линейно-независимыми мономами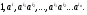

Подсчитаем число базисных элементов.

Число образующих равно 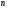, число мономов 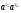- числу сочетаний из 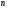элементов по 2, то есть 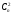, число мономов 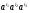- числу сочетаний из 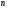элементов по 3, то есть 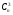, и так далее.

В результате число базисных элементов в соотношении (2) составляет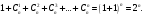

Таким образом, алгебру Грассмана можно рассматривать как линейное пространство размерности .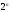

Список литературы.

1. Ван дер Варден Б.Л. Алгебра. М.: Наука, 1976.

2. Зорич В.А. Математический анализ. М.: Наука, 1981. Т.1.

3. Курош Л.Г. Курс высшей алгебры. М.: Наука, 1965.

4. Buchbinder I.L., Kuzenko S.M. Ideas and Method of Supersymmetry and Sypergravity or a Walk through Superspace.Bristol; Philadelphia:IOP Publ., 1995.