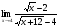Системы линейных алгебраических уравнений
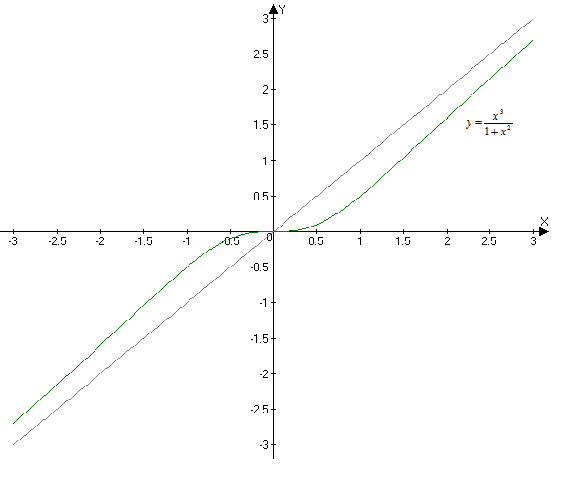
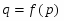
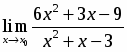
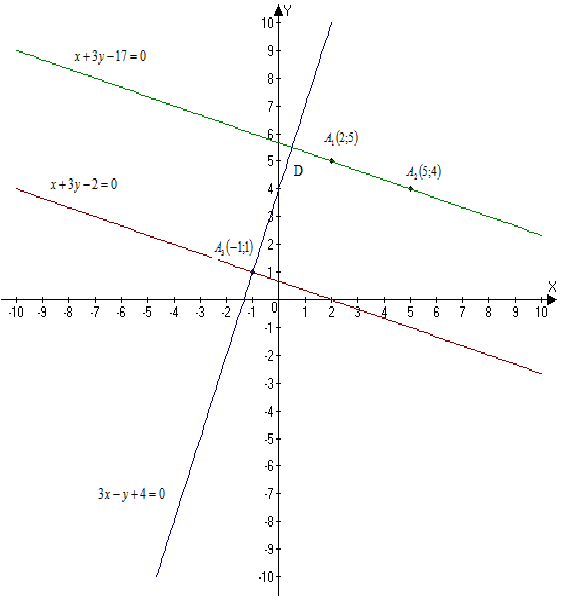
Высшая математика
Контрольная работа №1
Вариант 3
Задание №1
Дана система линейных алгебраических уравнений:
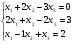
Требуется:
Записать матрицу коэффициентов (А) и свободных членов (
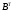 );
);Решить систему методом Гаусса и (в случае её невырожденности) Крамера.
Решение.
Запишем матрицу коэффициентов:
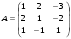
Матрица свободных членов:
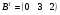
Решим систему методом Гаусса.
Запишем расширенную матрицу системы и преобразуем её методом Гаусса (приведём к ступенчатому виду с помощью элементарных преобразований строк):
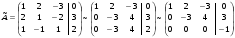
Шаг 1: из строки 2 вычитаем строку 1, умноженную на 2; из строки 3 вычитаем строку 1;
Шаг 2: из строки 3 вычитаем строку 2;
Получили вырожденную систему уравнений, так как если записать уравнение по последней строке преобразованной матрицы, получим 0 = -1, что неверно. Значит, заданная система не имеет решений.
Ответ: решения системы не существует.
Задание №2
Решить матричное уравнение:
АXBт + m AB = С
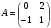 ,
, 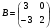 и
и 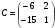 , m=2.
, m=2.
Решение.
Для того, чтобы решить заданное матричное уравнение, перенесём все известные слагаемые в правую часть, а неизвестные оставим в левой:
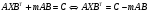
Затем обе части уравнения домножим справа на матрицу, обратную к транспонированной матрице В, и домножим слева на матрицу, обратную к матрице А, получим:
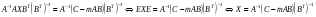
где Е – единичная матрица.
Для того, чтобы найти Х, найдём все необходимые матрицы, затем перемножим их.
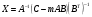 (*)
(*)
Запишем транспонированную матрицу Bт, для чего на место столбцов запишем соответствующие строки:
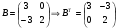
Вычислим произведение матриц А и В, затем умножим полученную матрицу на m=2:
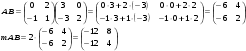
Вычтем полученную матрицу из матрицы С:
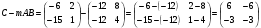
Теперь найдём матрицы 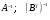 .
.
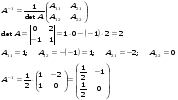
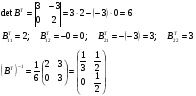
Подставляем все найденные матрицы в уравнение (*)
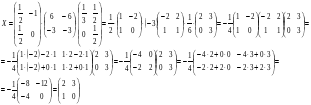
Ответ: 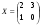 .
.
Задание №3
Даны векторы:
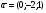 ,
, 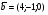 и
и 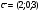 .
.
Требуется:
– найти длину вектора
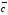 ;
;- вычислить скалярное произведение
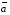
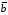 ;
;– найти координаты вектора
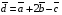 ;
;– установить, является ли система векторов
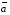 ,
,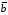 ,
,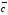 линейно зависимой.
линейно зависимой.
Решение.
Длина (модуль) вектора
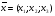 находится по формуле:
находится по формуле:
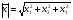
Значит, длина вектора 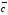 равна:
равна:
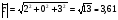
Скалярное произведение векторов
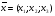 и
и 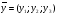 ищется следующим образом:
ищется следующим образом:
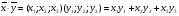
Подставляем координаты векторов 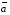 и
и 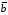 .
.
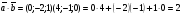
Сложение и вычитание векторов заключается в поэлементном соответственно сложении или вычитании их координат. Чтобы умножить вектор на число, необходимо умножить каждую координату вектора на это число. Поэтому:
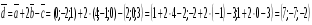
Для того, чтобы определить, является ли система из трёх векторов, линейно независимой, достаточно вычислить определитель третьего порядка, составленный из координат этих векторов. Если определитель окажется равным 0, значит, система векторов линейно зависима; если определитель будет отличен от 0 – система векторов линейно независима. Координаты векторов будут строками определителя. Вычислим определитель, разложив его по первому столбцу.
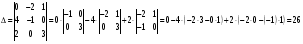
Так как определитель не равен 0, значит, система векторов линейно независима.
Ответ: 1) 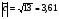 ; 2)
; 2) 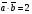 ; 3)
; 3) 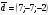 ; 4) система векторов линейно независима.
; 4) система векторов линейно независима.
Задание №4
Даны координаты точек: 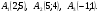
Требуется:
найти общее уравнение прямой
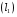 , проходящей через точки А1 и А2;
, проходящей через точки А1 и А2;найти уравнение прямой
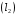 , проходящей через точку
, проходящей через точку 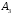 параллельно прямой
параллельно прямой 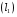 ;
;найти расстояние между прямыми
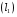 и
и 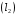 ;
;написать уравнение прямой, проходящей через точку
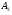 перпендикулярно прямой
перпендикулярно прямой 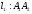 и найти координаты точки пересечения этих прямых;
и найти координаты точки пересечения этих прямых;построить схематический чертеж.
Решение.
Сначала запишем уравнение прямой, проходящей через две точки М1(x1,y1) и М2(x2,y2):
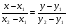
Подставляем координаты точек А1 и А2 и получаем:
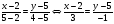
Преобразуем полученное уравнение и получим общее уравнение прямой 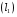 :
:
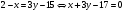
Запишем уравнение прямой
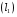 в виде
в виде 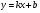 :
:
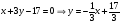
Если прямые параллельны, то они имеют одинаковый коэффициент k. Значит прямая 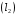 имеет вид
имеет вид 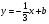 . Так как она проходит через точку
. Так как она проходит через точку 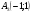 , значит можем подставить координаты этой точки и найти b:
, значит можем подставить координаты этой точки и найти b:
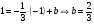
Уравнение прямой 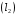 :
: 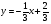 или
или 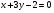
Если две параллельные прямые заданы общими уравнениями
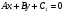 и
и 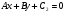 , то расстояние между ними можно вычислить по формуле:
, то расстояние между ними можно вычислить по формуле:
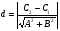
Подставляя коэффициенты из уравнений прямых 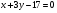 и
и 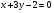 , получаем:
, получаем:
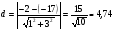
Уравнение прямой, проходящей через точку М1(x1,y1) и перпендикулярной к прямой
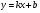 , представляется уравнением:
, представляется уравнением:
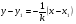
Подставим координаты точки 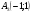 и коэффициенты уравнения прямой
и коэффициенты уравнения прямой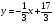 :
:
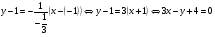
Координаты точки пересечения прямых 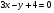 и
и 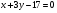 найдём, решив систему уравнений:
найдём, решив систему уравнений:
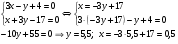
Координаты точки пересечения прямых D(0,5; 5,5).
На рисунке изобразим все необходимые прямые и точки:
Ответ: 1) 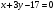 ; 2)
; 2) 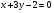 ; 3)
; 3) 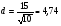 ; 4)
; 4) 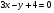 ; D(0,5; 5,5)..
; D(0,5; 5,5)..
Задание №5
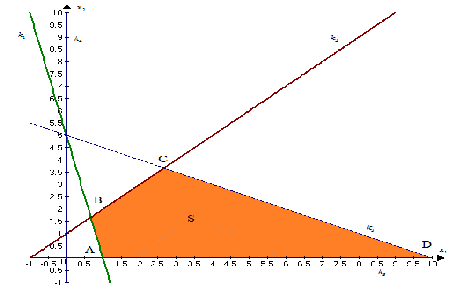
Построить на плоскости область решений и определить координаты угловых точек области решений системы неравенств:
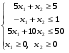
Решение.
Построим прямые:
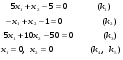
На рисунке изображены прямые и выделена интересующая нас область решений S.
Угловыми точками этой области являются точки А, В, С и D. Найдём их координаты, как координаты точек пересечения соответствующих двух прямых:
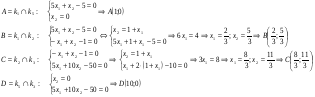
Итак, координаты угловых точек области решений неравенств:
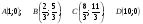
Ответ: 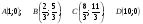 .
.
Задание №6
Не применяя правило Лопиталя, вычислить следующие пределы
1. , если: а) 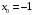 , б)
, б) 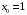 , в)
, в) 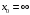 .
.
2. 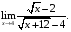
Решение.
а)
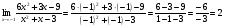
б) 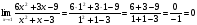
в) 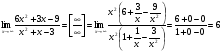
Введём замену 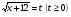 , тогда
, тогда 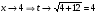 . Затем домножим числитель и знаменатель на выражение, сопряжённое числителю:
. Затем домножим числитель и знаменатель на выражение, сопряжённое числителю:
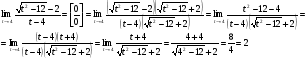
Ответ: 1) а) 2; б) 0; в) 6; 2) 2.
Задание №7
Задана функция спроса от цены товара . Найти эластичность спроса по цене 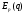 при цене
при цене 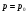 , и дать экономическую интерпретацию.
, и дать экономическую интерпретацию.
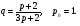
Решение.
Эластичность функции y относительно переменной х вычисляется по формуле
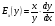
Вычислим производную функции q по p и подставим наши значения в формулу:
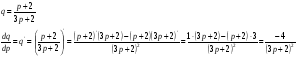
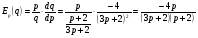
Подставим значение 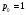 , тогда получим:
, тогда получим:
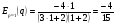
Полученное значение эластичности спроса по цене показывает, что если цена увеличится на 1%, то спрос снизится на 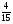 %.
%.
Ответ: 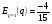 .
.
Задание №8
Исследовать функцию и построить ее график:
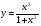
Решение.
Область определения функции
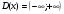
Функция не является периодической.
Функция является нечётной, так как

Так как функция нечётна, значит точка пересечения с осью Оу – это начало координат, т.е. точка (0; 0).
Точки пересечения с осью Ох: 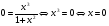 ,т.е. только точка (0; 0).
,т.е. только точка (0; 0).
y(x) непрерывна на всей области определения D(x), значит точек разрыва нет, вертикальных асимптот нет.
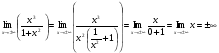
Так как пределы бесконечны, значит, горизонтальных асимптот нет.
Найдём наклонные асимптоты вида 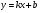 , если они есть:
, если они есть:
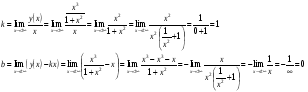
Прямая 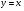 будет наклонной асимптотой.
будет наклонной асимптотой.
Найдём экстремумы функции и интервалы возрастания и убывания. Для этого найдём точки, в которых первая производная обращается в 0:
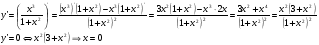
Т.е. критической является точка 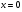 .
.
Но в точке x=0, производная не меняет знак, поэтому эта точка не является точкой экстремума.
На всей области определения функции y(x) производная 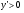 , следовательно, функция возрастает.
, следовательно, функция возрастает.
Найдём интервалы выпуклости и вогнутости кривой, а также точки её перегиба. Для этого найдём точки, в которой вторая производная меняет знак.
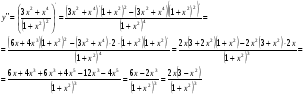
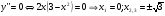
Значит, функция имеет три точки перегиба: 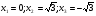 .
.
На каждом из промежутков 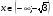 и
и 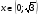 вторая производная
вторая производная 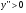 , следовательно, функция вогнута. На каждом из промежутков
, следовательно, функция вогнута. На каждом из промежутков 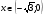 и
и 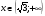 вторая производная
вторая производная 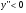 , следовательно, функция выпукла.
, следовательно, функция выпукла.
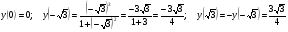
Построим график функции
Задание №9
Найти градиент функции в указанной точке:
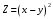 , М (1,1);
, М (1,1);
Решение.
Градиент функции в точке 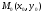 находится по формуле:
находится по формуле:
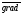
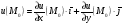
Вычислим частные производные заданной функции Z и их значения в точке 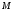 :
:
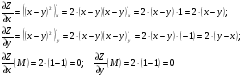
Подставим значения частных производных в точке 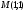 в формулу для вычисления градиента в точке, получим:
в формулу для вычисления градиента в точке, получим:
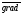
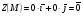
Ответ: 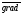
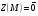 .
.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ