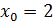
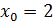
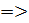
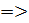
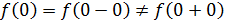
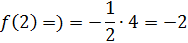
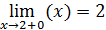
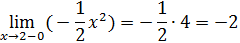
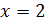
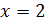
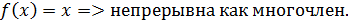
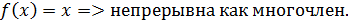
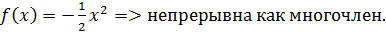
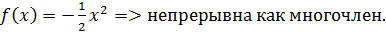
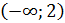
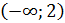
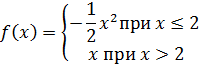
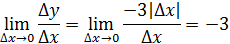
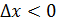
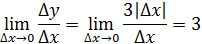
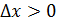
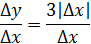
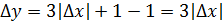
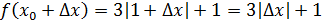
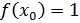
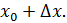
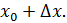
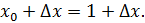
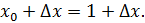
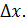
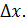
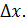
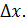
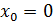
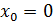
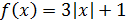
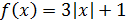
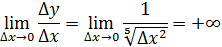
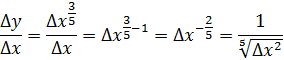
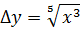
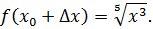
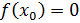
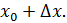
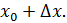
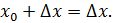
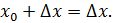
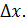
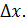
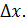
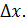
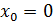
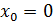
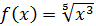
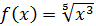
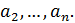
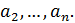
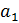
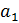
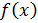
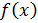
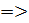
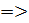
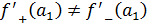
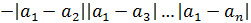
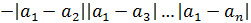
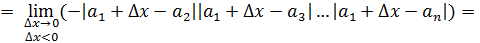
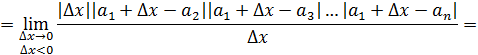
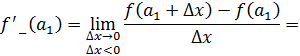
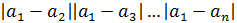
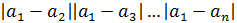
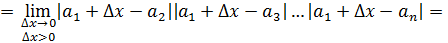
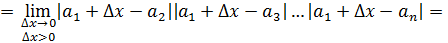
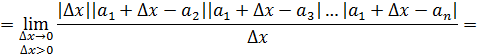
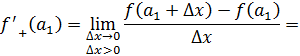
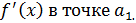
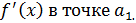
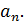
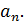
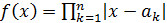
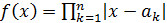
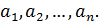
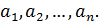
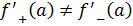
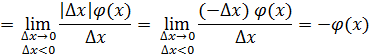
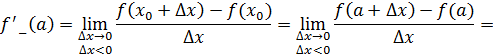
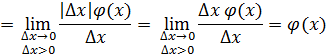
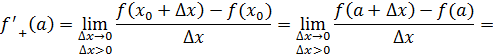
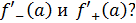
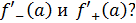
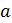
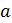
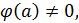
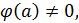
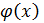
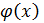
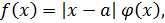
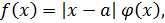
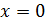
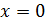
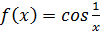
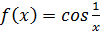
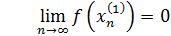
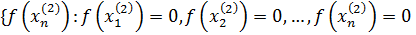
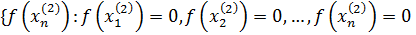
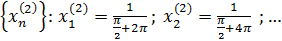
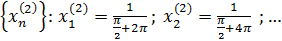
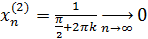
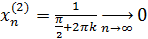
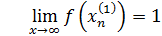
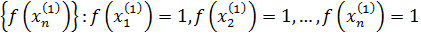
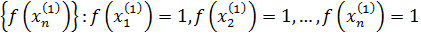
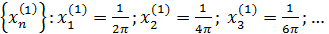
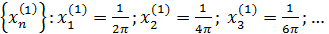
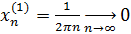
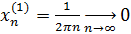
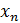
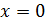
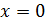
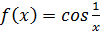
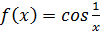
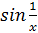
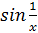
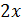
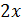
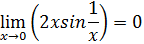
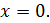
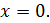
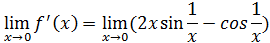
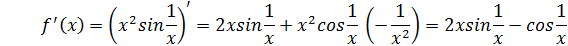
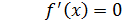
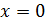
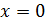
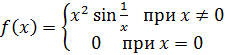
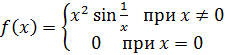
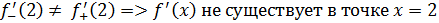
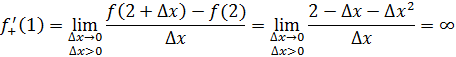
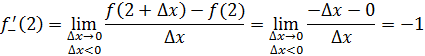
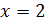
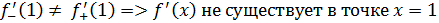
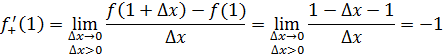
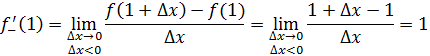
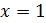
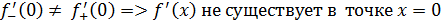
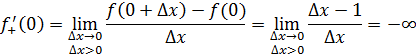
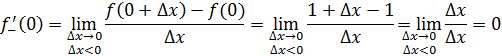
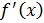
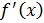
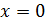
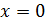
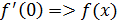
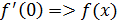
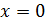
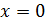
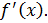
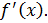
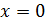
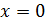
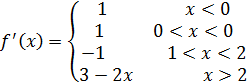
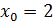
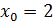
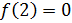
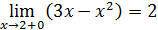
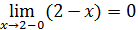
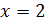
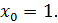
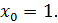
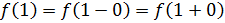
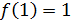
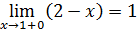
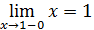
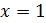
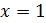
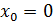
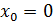
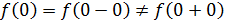
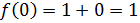
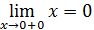
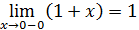
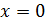
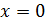
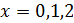
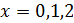
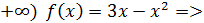
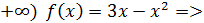
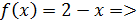
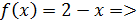
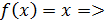
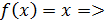
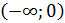
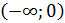
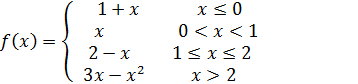
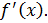
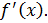
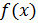
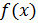
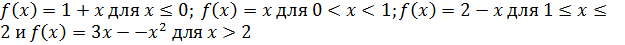
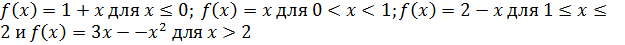
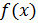
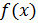
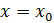
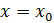
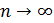
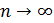
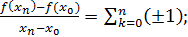
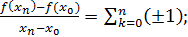
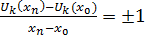
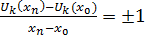
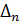
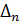
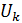
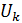
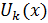
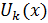
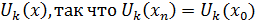
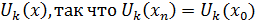
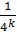
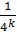
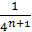
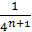
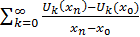
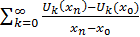
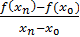
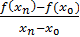
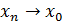
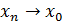
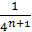
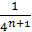
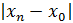
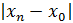
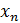
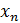
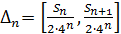
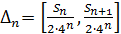
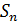
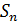
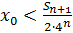
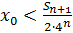
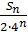
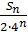
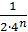
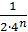
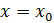
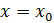
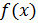
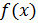
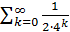
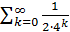
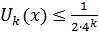
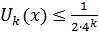
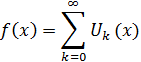
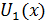
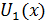
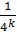
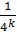
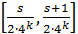
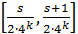
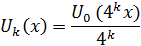
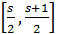
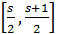
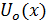
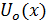
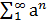
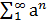
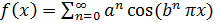
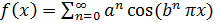
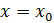
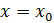
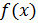
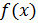
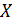
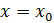
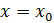
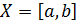
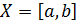
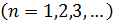
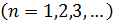
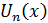
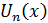
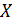
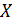
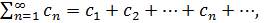
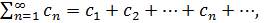
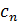
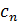
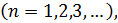
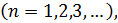
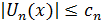
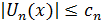
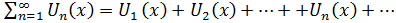
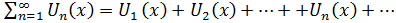
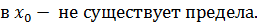
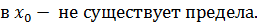
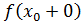
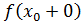
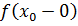
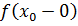
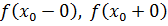
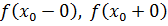
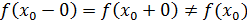
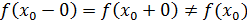
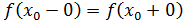
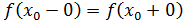
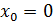
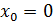
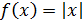
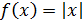
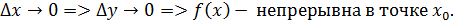
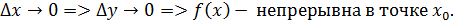
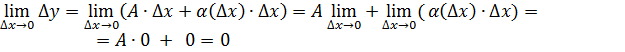
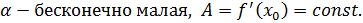
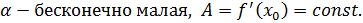
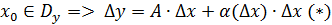
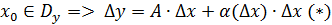
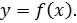
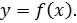
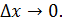
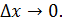
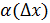
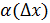
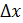
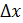
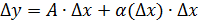
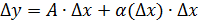
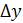
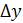
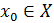
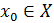
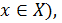
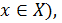
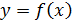
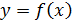
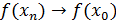
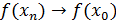
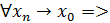
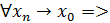
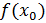
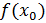
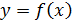
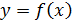
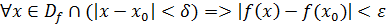
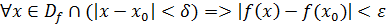
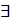
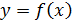
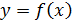
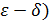
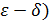
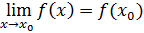
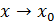
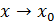
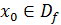
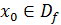
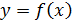
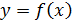
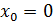
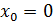
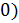
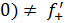
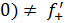
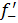
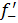
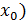
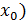
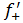
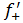
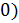
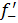
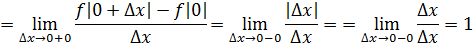
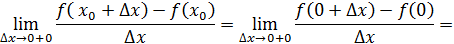
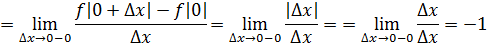
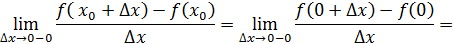
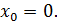
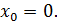
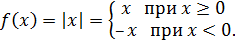
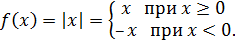
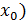
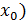
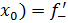
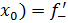
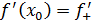
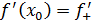
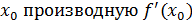
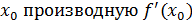
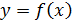
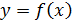
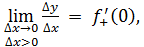
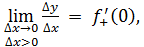
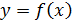
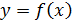
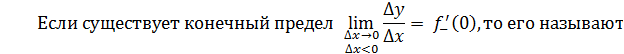
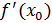
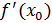
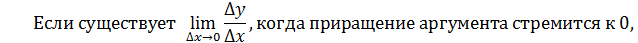
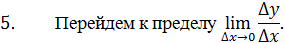
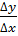
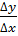
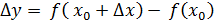
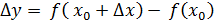
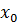
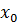
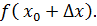
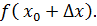
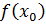
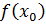
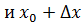
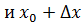
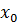
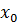
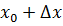
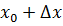
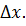
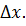
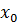
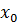
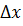
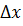
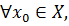
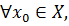
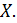
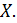
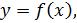
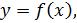
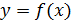
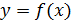
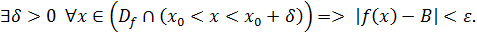
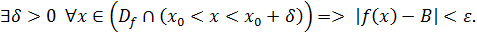
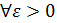
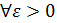
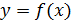
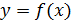
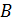
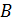
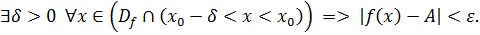
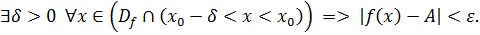
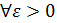
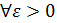
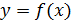
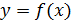
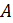
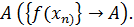
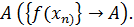
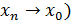
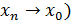
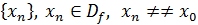
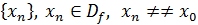
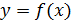
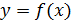
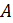
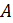
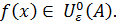
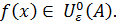
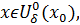
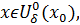
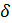
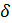
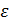
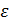
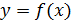
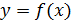
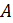
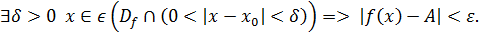
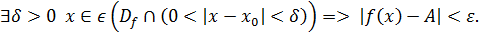
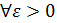
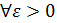
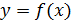
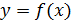
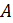
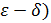
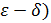МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«УССУРИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ»

Физико–математический факультет

Курсовая работа по математическому анализу

Тема: «Непрерывная, но не дифференцируемая функции»

Выполнила: Пляшешник Ксения

студентка 131 группы

Руководитель: Делюкова Я.В.

Уссурийск – 2011г.

Содержание

Введение

Курсовая работа посвящена изучению связи между непрерывностью и существованием производной функции одной переменной. Исходя из цели ставились задачи:

1. Изучить учебную литературу;

2. Изучить пример непрерывной функции, не имеющей производной ни в одной точке, построенной ван-дер-Варденом;

3. Прорешать систему упражнений.

Историческая справка

Ба́ртель Лее́ндерт ван дер Ва́рден (нидерл. Bartel Leendert van der Waerden, 2 февраля 1903, Амстердам, Нидерланды — 12 января 1996, Цюрих, Швейцария) — голландский математик.

Обучался в Амстердамском университете, затем в Гёттингенском университете, где на него огромное влияние оказала Эмми Нётер.

Основные работы в области алгебры, алгебраической геометрии, где он (наряду с Андре Вейлем и О.Зарисским) поднял уровень строгости, и математической физики, где он занимался приложением теории групп к вопросам квантовой механики (наряду с Германом Вейлем и Ю.Вигнером). Его классическая книга Современная алгебра (1930) стала образцом для последующих учебников по абстрактной алгебре и выдержала множество переизданий.

Ван дер Варден — один из крупнейших специалистов по истории математики и астрономии в Древнем мире. Его Пробуждающаяся наука (Ontwakende wetenschap 1950, русский перевод 1959) даёт развёрнутое изложение истории математики и астрономии в Древнем Египте, Вавилоне и Греции. В Приложении к русскому переводу этой книги опубликована статья «Пифагорейское учение о гармонии» (1943) — фундаментальное изложение пифагорейских взглядов на музыкальную гармонию.

Основные определения и теоремы

Предел функции в точке. Левые и правые пределы

Определение (предел по Коши, на языке Число называется пределом функции в точке , если

Определение (на языке окрестности) Число называется пределом функции в точке , если для любой -окрестности числа сущесвует - окрестность точки такая, что как только

Определение (по Гейне) Число называется пределом функции в точке , если для любой последовательности , сходящейся к ( то есть , соответствующая последовательность значений функции сходится к числу

Определение Число называется левым пределом функции в точке , если

Определение Число называется правым пределом функции в точке , если

Теорема (необходимое и достаточное условие существования предела)

Для того чтобы в точке существовал предел функции необходимо и достаточно, чтобы существовали левые и правые пределы равные между собой.

Понятие производной. Односторонние производные.

Рассмотрим функцию заданную на множестве

1. Возьмем возьмем приращение . Дадим точке приращение Получим .

2. Вычислим значение функции в точках . и

3. Найдем приращение функции в точке .

4. Составим отношение приращения функции в точке к приращению аргумента .

причем приращение аргумента может быть как положительным, так и отрицательным, то этот предел называется производной в точке и обозначают . Он может быть и бесконечным.

левой (левосторонней) производной функции в точке , а если

существует конечный предел то его называют правосторонней производной функции в точке .

Функция имеет в точке тогда и только тогда, когда в точке совпадают ее левая и правая производные:

((.

Рассмотрим функцию Найдем односторонние производные в точке

Следовательно, (=-1;(=1 и ((, то есть в точке функция производной не имеет.

Различные определения непрерывности функции в точке.

Определение 1 (основное) Функция называется непрерывной в точке , если предел функции при равен значению функции в этой точке.

Определение 2 (на языке Функция называется непрерывной в точке , если ε, δ>0, такое что .

Определение 3 (по Гейне, на языке последовательности) Функция называется непрерывной в точке , если для любой последовательности сходящейся к точке соответствующая последовательность значений функции сходится к .

Определение 4 (на языке приращений) Функция называется непрерывной в точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Понятие дифференцируемой функции

Определение 1 Функция , заданная на множестве (называется дифференцируемой в точке , если ее приращение в этой точке можно представить как (*), где A-const, независящая от , - бесконечно малая при

Определение 2 Функция, дифференцируемая в любой точке множества, называется дифференцируемой на множестве.

Связь между дифференцируемостью и непрерывностью

Теорема. Если функция дифференцируема в точке , то она непрерывна в точке .

Доказательство.

Пусть задана функция Функция дифференцируема в точке , где

При

Обратная теорема. Если функция непрерывна, то она дифференцируема.

Обратная теорема неверна.

в - не дифференцируема, хотя непрерывна.

Классификация точек разрыва

Определение Функция не являющаяся непрерывной в точке является разрывной в точке , а саму точку называют точкой разрыва.

Существуют две классификации точек разрыва: I и II рода.

Определение Точка называется точкой разрыва I рода, если в этой точке существуют конечные односторонние пределы неравные друг другу.

Определение Точка называется точкой устранимого разрыва, если , но они не равны значению функции в точке .

Определение Точка называется точкой разрыва II рода, если в этой точке односторонние пределы равны или один из односторонних пределов бесконечен или в точке не существует предела.

• – бесконечные;

• – бесконечный или – бесконечный;

Признаки равномерной сходимости рядов

Признак Вейерштрасса.

Если члены функционального ряда (1) удовлетворяют в области неравенствам где - член некоторого сходящегося числового ряда то ряд (1) сходится в равнмерно.

Теорема 1 Пусть функции определены в промежутке и все непрерывны в некоторой точке этого промежутка. Если ряд(1) в промежутке сходится равномерно, то и сумма ряда в точке также будет непрерывна.

Пример непрерывной функции без производной

Первый пример такого рода был построен Вейерштрассом; его функция определяется рядом:

,

где 0<a<1, а b есть нечетное натуральное число (причем ab>1+π). Этот ряд мажорируется сходящейся прогрессией , следовательно (признаки равномерной сходимости рядов), сходится равномерно, и его сумма является всюду непрерывной функцией от x. Кропотливым исследованием Вейерштрассу удалось показать, что тем не менее ни в одной точке для нее не существует конечной производной.

Здесь будет рассмотрен более простой пример ван-дер-Вардена, построенный по существу на той же идее, лишь колеблющиеся кривые у=cosωχ заменены колеблющимися ломаными.

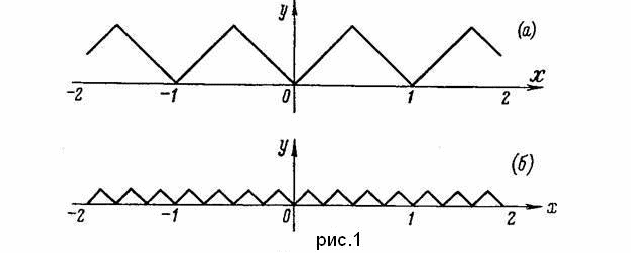
Итак, обозначим через абсолютную величину разности между числом χ и ближайшим к нему целым числом. Эта функция будет линейной в каждом промежутке вида , где s-целое; она непрерывна и имеет период 1. Ее график представляет собой ломаную, он изображен на рис.1; отдельные звенья ломаной имеют угловой коэффициент ±1.

Положим, затем, для к=1,2,3,…:

Эта функция будет линейной в промежутках вида ; она также непрерывна и имеет период . Ее график также ломаная, но с более мелкими зубчиками; на рис.1(б), например, изображен график функции . Во всех случаях угловые коэффициенты отдельных звеньев ломаной и здесь равны ±1.

Определим теперь, для всех вещественных значений x, функцию f(x) равенством

Так как, очевидно, 0≤ (k=0,1,2,…), так что ряд мажорируется сходящейся прогрессией , то (как и в случае функции Вейерштрасса) ряд сходится равномерно, и функция всюду непрерывна.

Остановимся на любом значении . Вычисляя его с точностью до (где n=0,1,2,…), по недостатку и по избытку, мы заключим его между числами вида:

≤ , где -целое.

(n=0,1,2,…).

Очевидно, что замкнутые промежутки оказываются вложенными один в другой. В каждом из них найдется такая точка , что расстояние ее от точки равно половине длины промежутка.

=;

Ясно, что с возрастанием n варианта .

Составим теперь отношение приращений

=

Но при k>n, число есть целое кратное периодам функции , соответствующие члены ряда обращаются в 0 и могут быть опущены. Если же k≤n, то функция , линейная в промежутке , будет линейной и в содержащемся на нем промежутке , причем

(k=0,1,…,n).

Таким образом, имеем окончательно иными словами, это отношение равно четному целому числу при нечетном n и нечетному числу при четном n. Отсюда ясно, что при отношение приращений ни к какому конечному пределу стремится не может, так что наша функция при конечной производной не имеет.

Решение упражнений

Упражнение 1 ([2], №909)

Функция определена следующим образом: . Исследовать непрерывность и выяснить существование

Решение

На непрерывна как многочлен;

На (0;1) непрерывна как многочлен;

На (1;2) непрерывна как многочлен;

На (2; непрерывна как элементарная функция.

- точки подозрительные на разрыв

Так как левый предел равен значению функции в точке, то функция разрывна в точке .

Так как левый предел равен правому пределу и равен значению функции в точке функция непрерывна в точке

Так как левый предел равен значению функции в точке, то функция разрывна в точке .

1 способ. В точке не существует конечной производной функции Действительно, предположим противное. Пусть в точке существует конечная производная функции непрерывна в точке (по теореме 1: Если функция дифференцируема в точке , то она непрерывна.

2 способ. Найдем односторонние пределы функции в точке x=0.

Упражнение 2 ([1], №991)

Показать, что функция имеет разрывную производную.

Решение.

Найдем производную функции.

При

При

Предел не существует разрывна в точке

Так как – бесконечно малая функция, - ограниченная.

Докажем, что функция в точке предела не имеет.

Для доказательства достаточно показать, что существуют две последовательности значений аргумента сходящиеся к 0, что не сходится к

Вывод: функция в точке предела не имеет.

Упражнение 3 ([1], №995)

Показать, что функция где - непрерывная функция и не имеет производной в точке . Чему равны односторонние производные

Решение.

Односторонние пределы не равны функция не имеет производной в точке .

Упражнение 4 ([1], №996)

Построить пример непрерывной функции, не имеющей производной функции в данных точках:

Решение.

Рассмотрим функцию в точках

Найдем односторонние пределы

=

=

Односторонние пределы не равны функция не имеет производной в точке . Аналогично, функция не имеет производных в остальных точках

Упражнение 5 ([4], №125)

Показать, что функция не имеет производной в точке .

Решение

Возьмем приращение Дадим точке приращение Получим

Найдем значение функции в точках и

Найдем приращение функции в точке

Составим отношение приращения функции в точке к приращению аргумента

Перейдем к пределу

Вывод: не имеет конечной производной в точке .

Упражнение 6 ([4], №128)

Показать, что функция не имеет производной в точке .

Решение

Возьмем приращение Дадим точке приращение Получим

Найдем значение функции в точках и

Найдем приращение функции в точке

Составим отношение приращения функции в точке к приращению аргумента

Перейдем к пределу

Вывод: не имеет конечной производной в точке .

Упражнение 7 ([4], №131)

Исследовать функцию на непрерывность

Решение.

На

На

– точка подозрительная на разрыв

Так как левый предел равен значению функции в точке, то функция непрерывна в точке существует разрыв Iрода.

Заключение

В курсовой работе излагается материал, связанный с понятием «Непрерывная, но не дифференцируемая функции», цели данной работы достигнуты, задачи решены.

Список литературы

1. Б. П. Демидович, / Сборник задач по курсу математического анализа. Учебное пособие для студентов физико-математического факультета педагогических институтов. – М.: Просвещение, 1990 –624с.

2. Г. Н. Берман, / Сборник задач по курсу математического анализа. – М.: Наука, 1977 – 416с.

3. Г. М. Фихтенгольц, / Курс дифференциального и интегрального исчисления т.II. - М., Наука, 1970- 800с.

4. И.А. Виноградова, /Задачи и упражнения по математическому анализу ч.1. – М.:Дрофа,2001 – 725с.

5. Ресурс Интернет \ http://ru.wikipedia.org/wiki.

6. Ресурс Интернет \http://www.mathelp.spb.ru/ma.htm.