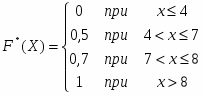
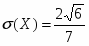
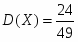
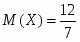
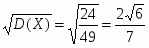
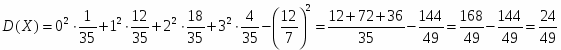
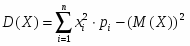
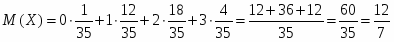
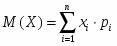
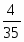
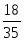
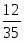
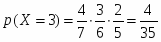
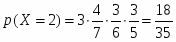
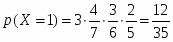
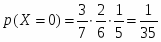
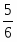
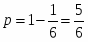
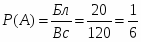
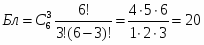
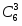
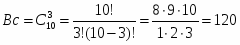
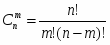
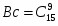
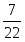
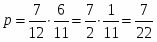
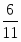
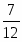
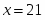
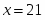
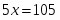
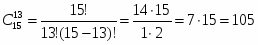
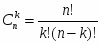
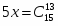Вариант 2

1. Решите уравнение

Решение:

По определению .

Тогда и уравнение принимает вид откуда получаем .

Ответ: .

2. В урне находится 7 белых и 5 черных шаров. Найти вероятность того, что два одновременно изъятых шара будут белыми.

Решение:

Изначально в урне 12 шаров и вероятность извлечь первый шар белый составляет . После того как извлечен первый белый шар в урне остается 11 шаров, из них 6 белых, следовательно вероятность извлечь второй белый шар составит .

В итоге вероятность совместного появления двух белых шаров равна:

Ответ: .

3. В ящике 10 деталей, из которых 4 стандартные. Контролер взял наудачу 3 детали. Найти вероятность того, что хотя бы одна из изъятых деталей окажется стандартной.

Решение:

События «хотя бы одна стандартная» и «все детали не стандартные» противоположны и сумма их вероятностей равна 1.

Найдем вероятность того, что 3 извлеченных детали не стандартные.

Общее число возможных элементарных исходов выбора 3-х деталей из 10 равно числу сочетаний из 10 элементов по 3: , где , тогда

Определим число исходов, благоприятствующих интересующему нас событию А (среди 3-х выбранных деталей 3 не стандартных). Три детали из 6 имеющихся можно выбрать способами следовательно, число благоприятствующих исходов .

Искомая вероятность равна отношению числа исходов, благоприятствующих нужному событию, к числу всех элементарных исходов: .

Тогда искомая вероятность того, что хотя бы одна из изъятых деталей окажется стандартной равна:

Ответ: .

4. В коробке 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекается 3 карандаша. Х – число красных карандашей. Найти закон распределения случайной величины Х, функцию распределения и основные числовые характеристики.

Решение:

Среди 3-х извлеченных карандашей может быть 0, 1, 2 или 3 красных.

Найдем вероятность каждого исхода.

0 красных:

1 красный:

2 красных:

3 красных:

Закон распределения принимает вид:

Х

0

1

2

3

р

Запишем функцию распределения полученной случайной величины Х:

Математическое ожидание М(Х) дискретной случайной величины находится по формуле:

,

и подставляя данные получим:

Дисперсию дискретной случайной величины можно вычислить по формуле:

,

и, подставляя данные, получим:

Среднеквадратичное отклонение: (Х)=

Ответ: ;

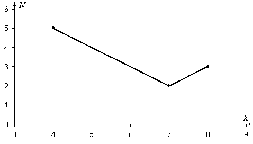
5. По данной выборке постройте полигон. Найти эмпирическую функцию.

Хi

4

7

8

Ni

5

2

3

Решение:

Построим полигон частот – ломаную, соединяющую точки с координатами (Хi; Ni).

Объем выборки равен N = 5 + 2 + 3 = 10.

Найдем относительные частоты и составим эмпирическую функцию распределения:

Хi

4

7

8

wi

0,5

0,2

0,3

Ответ: решение выше.