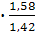
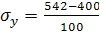
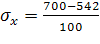
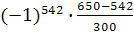
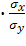
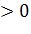
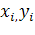
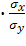
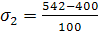
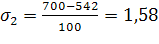
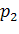
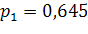
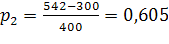
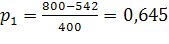
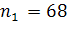
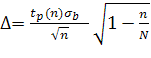
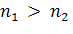
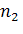
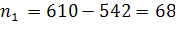
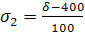
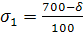
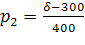
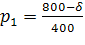
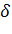
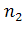
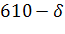
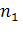
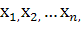
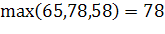
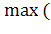
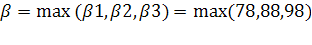
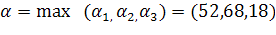
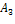
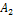
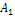
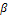
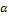
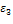
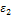
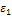
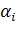
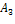
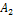
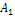
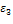
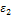
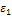
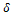
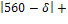
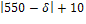
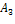
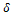
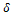
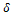
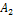
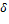
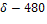
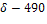
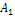
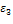
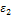
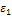
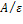
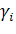
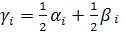
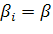
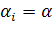
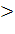
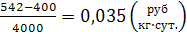
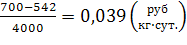
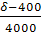
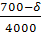
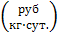
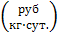
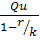
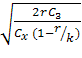
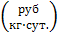
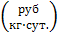
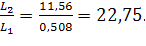
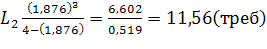
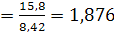
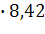
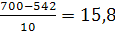
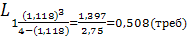
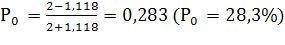
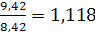
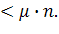
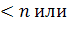
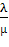
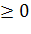
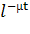
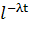
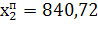
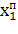
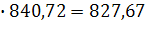
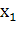
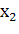
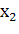
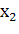
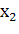
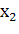
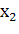
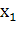
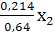
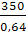
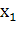
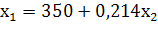
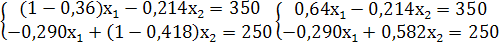
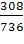
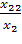
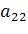
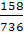
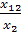
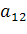
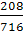
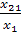
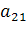
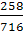
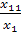
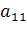
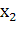
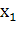
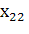
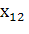
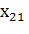
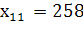
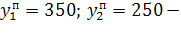
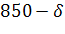
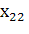
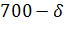
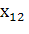
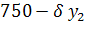
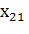
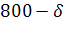
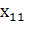
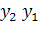
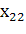
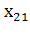
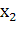
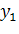
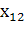
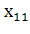
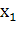
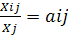
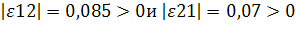
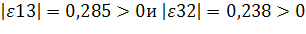
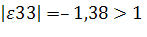
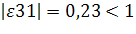
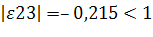
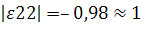
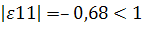
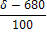
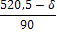
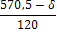
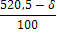
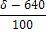
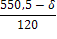
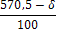
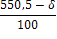
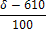
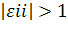
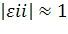
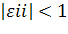
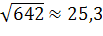
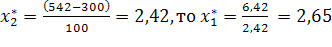
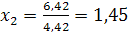
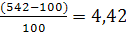
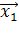
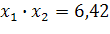
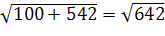
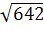
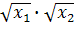
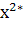
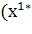
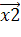
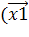
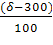
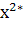
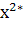
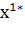
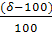
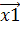
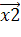
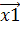
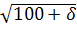
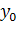
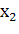
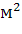
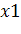
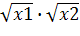
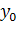
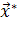
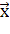
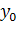
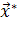
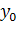
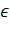
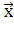
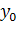
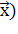
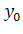
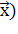
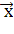
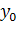
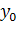
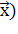
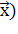
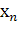
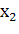
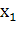
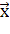
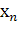
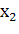
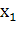
Экономико-математические методы

Вариант №40 (δ = 542)

Задание 1. Производственные функции

1.1 Дайте понятия производственной функции и изокванты. Что означает взаимозаменяемость ресурсов?

Пусть для производства некоторого продукта в количестве y единиц используются различные ресурсы: , ,...,выраженные в соответствующих единицах. Если принята закономерность получения продукта y из ресурсов =(, ,...,)т.е. если в явном виде выражена зависимость y=f(, то такая функция f(, называется производственной.

Пусть зафиксировано некоторое число . Множество в n-мерном пространстве, определяемое равенством

Q={:f(=}

называется изоквантой функции f( уровня

Из самого определения изокванты следует, что если Q, ∈Q, то ресурсы и обеспечивают производство одного и того же количества продукта , т. е. являются в этом смысле взаимозаменяемыми. Для организаторов производства знание изокванты позволяет недостаток одних ресурсов компенсировать увеличением других.

1.2 Производственная функция для райпо имеет вид

f(X1,X2)=10,

где f – товарооборот (млн руб.); – производственная площадь (тыс. ); – численность работников (сотни чел.). Рассмотрите изокванту уровня

=и найдите на ней точку C1с координатами , , где

=

и точку С2 с координатами , , где

=.

Сделайте вывод о возможности замены ресурсов , ,)и , )

Полученные результаты изобразите графически.

Решение:

Из дано число δ = 542. Тогда уравнение изокванты:

10=, (

Возведя обе части в квадрат и разделив их на 100, получим:

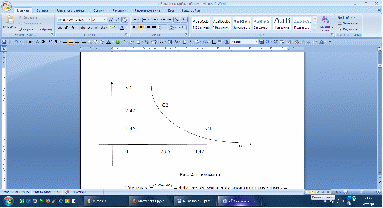
Найдем координаты точки C1 (рис. 2).

Рис. 2. Изокванта

Так как =, то из уравнения изокванты находим. Аналогично находим координаты точки C2. Так как

Итак, 145 работников райпо, используя 4,42 тыс. м2 производст-венной площади, обеспечат товарооборот млн руб., и такой же товарооборот могут обеспечить 242 работника райпо, используя площадь 2,42 тыс. м2.

Задание 2. Функция покупательского спроса

2.1 Дайте понятия малоэластичных, среднеэластичных и высокоэластичных товаров. Какие товары называются взаимозаменяемыми?

Классификация товаров на основе прямой и перекрестной эластичности сводится к следующему:

если , то i-й товар называется малоэластичным;

если, то i-й товар называется среднеэластичным;

если, то i-й товар называется высокоэластичным.

Если увеличение цены на j-й товар приводит к уменьшению спроса на i-й и наоборот, то эти товары называются взаимодополняемыми.

2.2 Произведите классификацию товаров по следующей таблице эластичностей

Товар

1-й

2-й

3-й

1-й

2-й

3-й

Пусть δ = 543. Тогда таблица эластичностей принимает вид:

Товар

1-й

2-й

3-й

1-й

–0,68

0,085

0,285

2-й

0,07

–0,98

–0,215

3-й

0,23

–0,238

–1,38

Так как, то 1-й товар малоэластичный;

так как, то 2-й товар среднеэластичный;

Так как, то товар малоэластичный;

Так как, то товар малоэластичный;

так как, то 3-й товар высокоэластичный.

Поскольку то 1-й и 3-й товары взаимозаменяемые.

Поскольку то товары взаимозаменяемые.

Задание 3. Межотраслевой баланс

3.1 Дайте определение коэффициентов прямых затрат. Где они могут быть использованы?

Отношение называется коэффициентом прямых затрат, означает объем продукции i-й отрасли, который требуется передать j-й отрасли, чтобы последняя произвела единицу своей валовой продукции.

Модель межотраслевого баланса может использоваться в планировании деятельности отраслей материального производства. Если технологии производства продуктов не меняются, то коэффициенты прямых затрат остаются неизменными.

3.2 За отчетный период имел место следующий баланс продукции

=++

=++=300

=

==220

=

=

а) вычислите коэффициенты прямых затрат;

б) вычислите плановый объем валовой продукции отраслей при плане выпуска конечной продукции:при условии неизменности технологии производства.

Решение:

=208

=158

=308

=258+158+300=716

=208+308+220=736

а. Вычислим коэффициенты прямых затрат:

===0,36

===0,290

===0,214

===0,418

б. Вычислим плановый объем валовой продукции отраслей:

0,64

=+

=546,875+0,334

-0,290(546,875+0,334)+0,582=250

0,582-0,096=250+158,59

=840,72

=546,875+0,334

Таким образом,=827,67 – плановый объем валовой продукции первой отрасли;

– плановый объем валовой продукции второй отрасли.

Задание 4. Системы массового обслуживания

4.1 Дайте описание входящего потока требований и каналов обслуживания. Какие экономические показатели характеризуют работу СМО?

К системам массового обслуживания относятся магазины, рестораны, автозаправочные станции, аэродромы, автоматизированные телефонные станции и многие другие объекты.

Для входящего потока требований предположим, что интервалы между поступлениями соседних требований есть случайная величина X с показательным законом распределения, т. е. ее интегральная функция F(t) имеет вид:

F(t)=1-

Число λ (треб./ед. времени) называется интенсивностью входящего потока, она показывает, сколько в среднем требований поступает в единицу времени.

Будем считать, что очередь не ограничена и требования обслуживаются в порядке поступления.

Для обслуживания примем предположения о том, что все n каналов одинаковы и для каждого из них время обслуживания одного требования есть случайная величина Y, распределенная по показательному закону, т. е. ее интегральная функция имеет вид:

F(t)=1-, t

Число μ (треб./ед. времени) называется интенсивностью обслуживания, она показывает, сколько требований обслуживается в единицу времени.

Обозначим

α =

(α – параметр загрузки СМО) и предполо-жим, что выполняется условие стационарности α λ (8)

Условие (8) означает, что интенсивность входящего потока меньше, чем суммарная интенсивность обслуживания.

4.2 В магазине самообслуживания работают две кассы с интенсивностью μ=(δ=300)/100 треб./мин. каждая. Входящий поток требований имеет интенсивность λ=(δ+400)/100 треб./мин. Рассчитайте долю времени простоя касс и среднюю длину очереди. Если интенсивность входящего потока станет равной λ= (700-δ)/10 треб./мин., то будет ли выполнено условие стационарности? Если будет, то во сколько раз увеличится средняя длина очереди?

Решение:

Пусть δ=542. Тогда μ=8,43 треб./мин., а первоначальное значение λ равно 9,42 треб./мин.

α=.

Если интенсивность λ станет равной треб./мин., то в силу неравенства 15,8<2 условие стационарности СМО выполнено, и можно вычислить среднюю длину очереди:

α

Итак, при интенсивности обслуживания μ=8,42 треб./мин. и интенсивности входа λ=9,42 треб./мин. доля времени простоя касс составляет 28,3% времени, а средняя длина очереди равна 0,508 треб. Если же интенсивность входа станет равной 15,8 треб./мин., то средняя длина очереди увеличится в 22,75 раза.

Задание 5. Модели управления запасами

5.1 Сформулируйте задачу оптимального управления запасами

Задача оптимального управления запасами будет формулироваться следующим образом: определить объем q заказываемой партии товара, при котором достигается минимум затрат на складские операции в единицу времени в предположении, что темп поступления заказанного товара превышает норму спроса на него.

5.2 Дайте экономическую интерпретацию предельной арендной плате

Экономически λ интерпретируется как предельная (максимальная) арендная плата за использование дополнительных складских емкостей. Если фактическая арендная плата α меньше либо равна предельной λ т. е. α≤λ, то аренда выгодна, и объем заказываемой партии вычисляется по формуле (10)

q=.

Если же α>λ, то аренда невыгодна, и тогда объем заказа надо уменьшать, он рассчитывается в этом случае по формуле (13)

q= .

5.3 Сделайте вывод о целесообразности аренды дополнительных складских емкостей или о необходимости сокращения объема заказываемой партии товара с учетом имеющихся складских емкостей при сравнении фактической α и предельной λ арендной платы за хранение единицы товара в единицу времени

α=

λ=

Решение:

α= , λ=

α λ

Вывод: фактическая арендная плата больше предельной арендной платы. Следовательно аренда дополнительных складских емкостей невыгодна. Объем заказываемой партии следует сократить до таких пределов, чтобы возникший товарный запас можно было разместить в имеющихся складских емкостях.

Задание 6. Модели теории игр

6.1 Объясните смысл элементов платежной таблицы и способы выбора стратегий с позиций крайнего пессимизма, крайнего оптимизма и оптимизма-пессимизма

Предлагается выбирать стратегию, соответствующую величине H.

При λ=0 H=max, и этот подход превращается в подход с позиции крайнего пессимизма.

При λ=1 H=max1, и этот подход превращается в под-ход с позиции крайнего оптимизма.

Величина H при изменении λ от 0 до 1 непрерывно изменяется от α до β, и выбор некоторого промежуточного λ соответствует сочетанию пессимизма и оптимизма при выборе стратегии. Возьмем, например, λ=0,5 и вычислим

а затем выберем наибольшее γ=max()

Стратегию, на которой достигается величина γ, будем называть соответствующей подходу с позиции пессимизма-оптимизма.

6.2 Выберите стратегии с позиций крайнего пессимизма, крайнего оптимизма и оптимизма-пессимизма для следующей платежной матрицы:

620-

610-

620-

630-

10

640-

Укажите соответствующие выигрыши.

Для числа δ = 542 таблица приобретает вид:

A ε

52

62

78

68

78

88

18

28

98

Выберем по каждой строке минимальное из чисел , максимальное βi, а затем вычислим их полусумму γi и получим матрицу:

A ε

i

i

γi

52

62

78

52

78

65

68

78

88

68

88

78

18

28

98

18

98

58

=68

=98

γ= γ1, γ2, γ3)=

Так как α=68, и это число находится в строке, соответствующей A2, то A2 – стратегия крайнего пессимизма, ожидаемый выигрыш равен 68 единицам. Так как β=98, и это число находится в строке, соответствующей A3, то A3– стратегия крайнего оптимизма, ожидаемый выигрыш равен 98 единицам. Так как γ=78, и это число находится в строке, соответствующей A2 , то A2 – стратегия оптимизма-пессимизма, ожидаемый выигрыш равен 78 единицам.

Задание 7. Эконометрические модели. Выборочный метод

7.1 Дайте понятия генеральной и выборочной совокупностей

Генеральной совокупностью называется множество однородных объектов, изучаемых относительно некоторого количественного признака или группы признаков. Количество объектов в этой совокупности называют объемом генеральной совокупности, при этом предполагается, что признак Х имеет значения для каждого из элементов совокупности.

Зачастую изучение всей генеральной совокупности объектов относительно определенного признака по ряду причин обусловлено большими трудностями или же вообще невозможно. Тогда изучение осуществляется на основе выборочной совокупности, которая формируется из генеральной отбором объектов случайным образом. Объем n выборочной совокупности существенно меньше объема N генеральной совокупности.

7.2 Определите соотношения между доверительными интервалами

а) при фиксированных значениях среднеквадратического отклонения σ, надежности P и различных значениях объема выборки:

=

=-490

б) при фиксированных значениях среднеквадратического отклонения σ, объема выборки n и различных значениях надежности:

в) при фиксированных значениях надежности P, объема выборки n и различных значениях среднеквадратического отклонения:

а)

=542-490=52

Объемы выборок находятся в соотношении . Тогда из формулы нахождения погрешности

(15)

следует, что при возрастании объема выборки n значение Δ уменьшается и Δ1<Δ2, т. е. доверительный интервал, соответствующий объему выборки , будет меньше доверительного интервала, соответствующего объему выборки n2=52.

б)

Исходя из формулы (15) следует, что при возрастании надежности P значение увеличивается, так как увеличивается значение функции Стьюдента tp(n). Следовательно, Δ1>Δ2, т. е. доверительный интервал, соответствующий надежности , будет больше доверительного интервала, соответствующего надежности =0,605

в)

=1,42

Исходя из формулы (15) следует, что при возрастании среднеквадратического отклонения значение Δ увеличивается. Следовательно, Δ1>Δ2, т. е. доверительный интервал, соответствующий среднеквадратическому отклонению σ1=1,58, будет больше доверительного интервала, соответствующего среднеквадратическому отклонению σ2=1,42.

Задание 8. Эконометрические модели. Корреляционные методы

8.1 Дайте понятия функциональной и корреляционной зависимостей

Функциональная зависимость – это такая связь между результативными и факторными признаками, когда значение результативного при-знака-функции полностью определяется значениями факторных признаков.

Корреляционная зависимость – это такая связь между признаками, когда определенным значениям факторных признаков соответствует множество случайных значений результативного признака. Например, зависимость веса человека от роста: множество людей, имеющих одинаковый рост, обладают различным весом.

8.2 Дайте определение коэффициента корреляции. Каковы его смысл и свойства?

Особое место в анализе взаимосвязей между результативным и факторным признаками занимает выявление тесноты связи между ними, которая характеризуется при линейной корреляционной связи коэффициентом корреляции r. Он рассчитывается по формуле

r=b

где σx, σy– среднеквадратические отклонения факторного x и результативного y признаков.

Если r=1, то все точки (), расположены на прямой и связь между признаками y и x самая сильная – функциональная. Если r, то связь называют прямой, т. е. с возрастанием значения факторного признака возрастает значение результативного. При r<0 – связь обратная, т. е. с возрастанием значения факторного признака значение результативного убывает. Таким образом, знак определяет направление связи (прямая, обратная). При r=0 признаки y и x называют некоррелированными.

8.3 Оцените тесноту связи и направление связи между признаками x и y, если известны: b– коэффициент регрессии, σx, σy – среднеквадратические отклонения признаков x и y

Направление и теснота связи между признаками и оцениваются на основе коэффициента корреляции, который рассчитывается по формуле

r=b

В данном случае

b==-0,359

=1,58

=1,42

r=-0,359=-0,400

r=-0,400

Коэффициент корреляции показывает, что связь между признаками x и y умеренная и обратная, т. е. при возрастании факторного признака x значение результативного признака y уменьшается.

Список использованной литературы

1. Антонов А. В. Системный анализ: учебник для вузов / А. В. Антонов. – М.: Высш. шк., 2004. – 454 с.

2. Сурмин Ю. П. Теория систем и системный анализ: учебник для вузов / Ю. П. Сурмин. – М.: МАУП, 2003. – 368 с.

3. Бабенко Л.О., Лабскер Л.Г. Игровые методы в управлении экономикой и бизнесом. – М.: Дело, 2001.