по Алгебре и геометрие
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Алгебра и геометрия
Выполнил: Шевыряев А.Н.
Группа: СДТ-03
Вариант:6
Проверил: ___________________
Новосибирск, 2010 г
Задача 1. Дана система трех линейных уравнений. Найти решение ее двумя способами: методом Крамера и методом Гаусса.
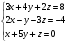
Решение системы методом Крамера.
Формулы Крамера:
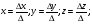
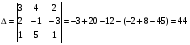
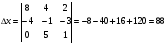
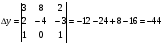
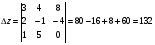
Найдем значения неизвестных:
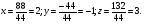
Выполним проверку:
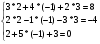
Решение системы методом Гаусса.
Составим расширенную матрицу системы:
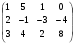
Выполним преобразования:
умножим первую строку на (-2) и сложим со 2-й строкой матрицы;
умножим первую строку на (-3) и сложим с 3-й строкой матрицы;
умножим 2-ю строку на (-1) и сложим с 3-й строкой матрицы.
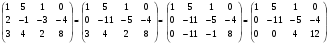
В результате получили матрицу системы треугольного вида.
Запишем итоговую систему:
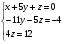
Найдем значения неизвестных: 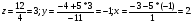
Задача 2. Даны координаты вершин пирамиды 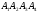 . Найти:
. Найти:
длину ребра
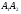 ;
;угол между ребрами
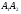 и
и 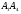 ;
;площадь грани
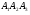 ;
;уравнение плоскости
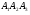 .
.объём пирамиды
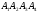 .
.
Решение.
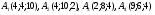
Рисунок 1.

Длина ребра равна расстоянию между точками
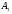 и
и 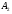 или модулю вектора
или модулю вектора 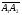 . Расстояние между точками
. Расстояние между точками 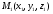 и
и 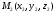 вычисляется по формуле
вычисляется по формуле 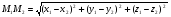 . Подставляя в эту формулу исходные данные, получим
. Подставляя в эту формулу исходные данные, получим 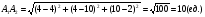
Угол между ребрами будем искать, используя формулы векторной алгебры:
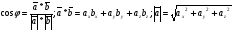
В нашем случае: 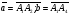
Чтобы найти координаты вектора, из координат конца вектора следует вычесть координаты начала вектора. Таким образом,
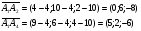
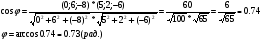
Площадь грани
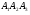 можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах
можно найти, используя свойства скалярного произведения: площадь параллелограмма, построенного на векторах 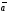 и
и 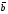 численно равна модулю их векторного произведения. В нашем случае
численно равна модулю их векторного произведения. В нашем случае
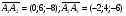
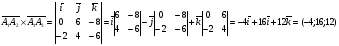
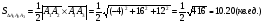
Уравнение плоскости
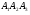 будем искать как уравнение плоскости, проходящей через три данные точки
будем искать как уравнение плоскости, проходящей через три данные точки 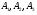 :
:
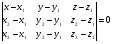 ;
;
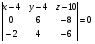 ;
;
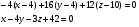
Полученное уравнение является уравнением плоскости 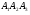 .
.
Объем пирамиды
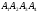 найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно
найдем, используя свойство смешанного произведения трех векторов – модуль смешанного произведения численно равен объему параллелепипеда, построенного на этих векторах. Соответственно 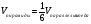
Найдем смешанное произведение векторов 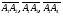 :
:
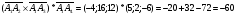
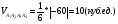

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ