Муниципальное бюджетное

общеобразовательное учреждение

«Средняя общеобразовательная

школа №3 «Пеликан»

Различные способы нахождения
наибольшего общего делителя двух натуральных чисел.

Математика.

Выполнил: Первухин

Дмитрий Евгеньевич

ученик 6 А класса,

Руководитель: Козлова

Наталья Дмитриевна,

учитель математики

г. Бердск. 2014 г.

Оглавление:

1. Введение……………………………………………………………………….2

1.2.Цель работы и ее задачи…………………………………………………2

2. Различные способы нахождения наибольшего общего делителя

двух натуральных чисел………………………………………………………

0. 2.1.Что такое НОД…………………………………………………………….2

1. 2.2. Свойства НОД…………………………………………………………….3

2.3. Метод полного перебора для нахождения НОД  натуральных чисел..5

2.4. Метод перебора делителей меньшего числа для нахождения

наибольшего общего делителя (НОД)  натуральных чисел…………...5

2.5. Метод нахождения наибольшего общего делителя (НОД)

натуральных чисел с помощью разложения на множители…………...6

2.6. Алгоритм Евклида нахождения наибольшего общего делителя

(НОД)  двух натуральных чисел вычитанием…………………………...6

2.7. Алгоритм Евклида нахождения наибольшего общего делителя

(НОД)  двух натуральных чисел делением………………………………7

2.8. Бинарный алгоритм Евклида нахождения наибольшего общего

делителя (НОД)  двух натуральных чисел………………………………7

2.9. Геометрический метод нахождения наибольшего общего

делителя (НОД)  натуральных чисел с помощью квадратов………….8

3. Выводы…...…………………………………………………………………….9

4. Список используемой литературы……………..…………………………….9

5. Приложение 1. Мои примеры нахождения наибольшего общего

делителя двух натуральных чисел (способы 1- 4)………………………….10

3. Приложение 2. Мои примеры нахождения наибольшего общего

делителя двух натуральных чисел (способы 5- 7)………………………….11

1. Введение

В начале этого учебного года на уроках математики мы познакомились с Наибольшим Общим Делителем (в дальнейшем для удобства будем называть его коротко НОД). Мы узнали, что такое НОД двух и более натуральных чисел и два способа его нахождения. Мы выяснили, что очень полезно уметь находить НОД двух чисел. Например, это может пригодиться, если мы захотим представить какое-нибудь рациональное число в виде дроби, имеющей по возможности меньший числитель и знаменатель. Или позволит найти красивые способы решения нестандартных текстовых задач.

Мне стало интересно, а есть ли другие способы нахождения НОД и, если есть, то, может быть они интереснее или рациональнее уже известных нам. Я заинтересовался этим и решил разобраться в этом вопросе подробнее.

1.2.Цель работы и её задачи

Цель работы:

1. Изучить различные способы нахождения НОД натуральных чисел;

2. Научиться пользоваться этими способами;

3. Выбрать самый удобный и рациональный.

Достижение этих целей возможно путем решения следующих задач:

1. Изучить литературу о наибольшем общем делителе;

2. Рассмотреть различные способы нахождения НОД;

3. Проверить эффективность найденных способов нахождения НОД на конкретных примерах.

2. Различные способы нахождения наибольшего общего делителя двух натуральных чисел.

2. 1. Что такое НОД двух чисел?

В школьном учебнике математики дается такое определение: наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем этих чисел.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел a или b не ноль.

Обозначения наибольшего общего делителя чисел a и b: НОД(a; b).

2.2. Свойства наибольшего общего делителя.

Наибольший общий делитель обладает рядом свойств. Перечислим основные  свойства наибольшего общего делителя (НОД).

Все свойства наибольшего общего делителя будем формулировать для положительных целых чисел, при этом будем рассматривать лишь положительные делители этих чисел.

1. Наибольший общий делитель чисел a и b равен наибольшему общему делителю чисел b и a, то есть, НОД(a; b)=НОД(b; a).

Это свойство НОД напрямую следует из определения наибольшего общего делителя.

2. Если a>b, то НОД(a; b) = НОД(a – b; b).

Иначе говоря, НОД двух натуральных чисел равен НОД их положительной разности (модуля их разности) и меньшего числа.

Легко доказать это свойство. Пусть k - общий делитель a и b (a> b). Это значит, что a = mk, b = nk, где m, n - натуральные числа, причем m > n. Тогда a - b = k(m - n), откуда следует, что k - делитель числа a - b. Значит, все общие делители чисел a и b являются делителями их разности a - b, в том числе и наибольший общий делитель. На этом свойстве основан алгоритм Евклида нахождения НОД двух чисел вычитанием.

3.Если a делится на b, то множество общих делителей чисел a и b совпадает с множеством делителей числа b, в частности, НОД(a;b)=b.

В частности, если числа a и b равны, то  НОД(а;b)=НОД(a;a)= НОД(b;b)=a=b. К примеру, НОД(132, 132)=132.

Данное свойство наибольшего делителя позволяет нам находить НОД двух чисел, когда одно из них делится на другое. При этом НОД равен одному из этих чисел, на которое делится другое число. Например,  НОД(8, 24)=8, так как 24 кратно восьми.

4. Если a=b·q+c, где a, b, c и q – целые числа, то множество общих делителей чисел a и b совпадает с множеством общих делителей чисел b и c, в частности, НОД(a, b)=НОД(b, c).

Обоснуем это свойство НОД.

Так как имеет место равенство a=b·q+c, то всякий общий делитель чисел a и b делит также и c (это следует из свойств делимости). По этой же причине, всякий общий делитель чисел b и c делит a. Поэтому совокупность общих делителей чисел a и b совпадает с совокупностью общих делителей чисел b и c. В частности, должны совпадать и наибольшие из этих общих делителей, то есть, должно быть справедливо следующее равенство  НОД(a, b)=НОД(b, c).

5. Сейчас мы сформулируем теорему, которая представляет собой алгоритм Евклида. Алгоритм Евклида позволяет находить НОД двух чисел.

Прежде чем дать формулировку теоремы, рекомендуем освежить в памяти теорему, которая утверждает, что делимое a может быть представлено в виде b·q+r, где b – делитель, q – некоторое целое число, называемое неполным частным, а r – целое число, удовлетворяющее условию 0≤ r< |b|, называемое остатком.

Итак, пусть для двух ненулевых целых положительных чисел a и b справедлив ряд равенств:

a = b·q₁ + r₁, 0< r₁< b

b = r₁·q₂ + r₂, 0< r₂< r₁

r₁ = r₂·q₃ + r₃, 0< r₃< r₂

r₂ = r₃·q₄ + r₄, 0< r₄< r₃

_·

_·

_·

r _k-2 = r_k-1·q_k + r_k, 0< r_k< r_k-1

r _k-1 = r_k·q_k+1
заканчивающийся, когда r_k+1=0 (что неизбежно, так как b>r₁>r₂>r₃, … - ряд убывающих целых чисел, и этот ряд не может содержать более чем конечное число положительных чисел), тогда r_k – это наибольший общий делитель чисел a и b, то есть, r_k=НОД(a, b).

Из рассмотренного свойства наибольшего общего делителя следует, что множество общих делителей чисел a и b совпадает с множеством делителей наибольшего общего делителя этих чисел. Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.

5. Пусть a и b – целые числа, одновременно не равные нулю, тогда существуют такие целые числа u₀ и v₀, то справедливо равенство  НОД(a, b)=a·u₀+b·v₀. Последнее равенство представляет собой линейное представление наибольшего общего делителя чисел a и b, это равенство называют соотношением Безу, а числа u₀ и v₀ – коэффициентами Безу.

6. Если m – любое натуральное число, то НОД(m·a, m·b)=m·НОД(a, b).

Обоснование этого свойства наибольшего общего делителя таково. Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД (m·a, m·b) = m·r_k, а r_k – это НОД(a, b). Следовательно, НОД(m·a, m·b)=m·НОД(a, b).

На этом свойстве наибольшего общего делителя основан способ нахождения НОД с помощью разложения на простые множители.

7. Пусть p – любой общий делитель чисел a и b, тогда НОД(a:p, b:p)= НОД(a, b):p, в частности, если p =НОД(a, b) имеем НОД (a:НОД(a, b), b : НОД(a, b))=1, то есть, числа a : НОД(a, b) и b:НОД(a, b) - взаимно простые.

Так как a=p·(a:p) и b=p·(b:p), и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД(a, b)= НОД(p·(a:p), p·(b:p))=p· НОД(a:p, b:p), откуда и следует доказываемое равенство.

Это свойство наибольшего общего делителя лежит в основе приведения обыкновенных дробей к несократимому виду.

8. Это свойство НОД, которое сводит задачу нахождения наибольшего общего делителя трех и большего количества чисел к последовательному отысканию НОД двух чисел.

Наибольший общий делитель чисел a₁, a₂, …, a_k равен числу d_k, которое находится при последовательном вычислении НОД(a₁, a₂)=d₂, НОД(d₂, a₃)=d₃,НОД(d₃, a₄)=d₄, …, НОД(d_k-1, a_k)=d_k.

Доказательство базируется на следствии из алгоритма Евклида. Общие делители чисел a₁ и a₂ совпадают с делителями d₂. Тогда общие делители чисел a₁, a₂ иa₃ совпадают с общими делителями чисел d₂ и a₃, следовательно, совпадают с делителями d₃. Общие делители чисел a₁, a₂, a₃ и a₄ совпадают с общими делителями d₃ и a₄, следовательно, совпадают с делителями d₄. И так далее. Наконец, общие делители чисел a₁, a₂, …, a_k совпадают с делителями d_k. А так как наибольшим делителем числа d_k является само число d_k, то НОД(a₁, a₂, …, a_k)=d_k.

На этом закончим обзор основных свойств наибольшего общего делителя и перейдем к различным способам его нахождения.

1 способ (следует из определения): Метод полного перебора для нахождения наибольшего общего делителя (НОД)  натуральных чисел.

1. Выписываем все делители числа а;

2. Выписываем все делители числа b;

3. Выбираем среди них общие делители;

4. Среди общих делителей выбираем самое большое число – это и есть НОД(a, b).

Например: Найти НОД(32;48).

Обозначим делители числа буквой D.

D (32) = {1; 2; 4; 8; 16; 32};

D (48) = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}.

D (32; 48) = {1; 2; 4}.

НОД(32; 48) = 4.

2 способ : Метод перебора делителей меньшего числа для нахождения наибольшего общего делителя (НОД)  натуральных чисел.

1. Найти делители меньшего из данных чисел.

2. Найти, начиная с большего, тот из выписанных делителей, который является также делителем другого числа.

3. Записать найденное число – НОД.

Например: Найти НОД(12;32).

D(12) = {1; 2; 3; 4; 6; 12}.

12 не является делителем числа 32;

6 не является делителем числа 32;

4- делитель 32.

НОД(12; 32) = 4.

Этот алгоритм легко реализуется, но его недостатком является то, что

необходимо проверять много вариантов. Это я показываю на примере нахождения НОД(195;156) (см. приложение 1).

3 способ; Метод нахождения наибольшего общего делителя (НОД) натуральных чисел с помощью разложения на множители.

1. Находим разложение чисел на простые множители.

2. Подчеркиваем общие числа.

3. Находим произведение подчеркнутых чисел у одного числа.

4. Записываем ответ.

Например:

Найти НОД(36; 48).

36=2•2•3•3,

48=2•2•2•2•3.

НОД(36,48)=2•2•3=12

Это способ часто удобен, но у него есть большой недостаток: разложить большое число на множители чрезвычайно трудно. Попробуйте найти, например, НОД(54739; 205 757).

Есть сравнительно простой алгоритм нахождения общего делителя двух чисел. Его приписывают Евклиду, одному из величайших математиков древности. Евклид жил в III-II в до н.э. в Александрии, а по другим источникам, в Дамаске. Оставил несколько сочинений, известных в латинских и арабских переводах, наиболее значительное из которых – состоящие из 13 книг «Начала» («Elements»)- представляет собой систематическое изложение математики того времени.

4 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД)  двух натуральных чисел вычитанием.

Древнегреческие математики называли этот алгоритм  ἀνθυφαίρεσις  или  ἀνταναίρεσις  — «взаимное вычитание». Этот алгоритм, видимо, не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.

1. Из большего числа вычитается меньшее.

2. Если получается 0, то числа равны друг другу и являются наибольшим общим делителем.

3. Если результат вычитания не равен 0, то большее число заменяется на результат вычитания

4. Переход к пункту 1.

Например: Найти НОД(30; 18).

30 - 18 = 12;
18 - 12 = 6;
12 - 6 = 6;
6 – 6 = 0.

НОД – это уменьшаемое или вычитаемое.

НОД (30; 18) = 6.

Приведенный метод вычисления не является оптимальным. Например, для нахождения НОД(100; 2) следует выполнить 50 (!!) операций вычитания (см. приложение 1). Для ускорения вычисления НОД операцию вычитания следует заменить операцией взятия остатка от деления.

5 способ: Алгоритм Евклида нахождения наибольшего общего делителя (НОД)  двух натуральных чисел делением.

1. Большее число делится на меньшее

2. Если делится без остатка, то меньшее число и есть наибольший общий делитель.

3. Если есть остаток, то большее число заменяем на остаток от деления.

4. Продолжаем деление до тех пор, пока не получим в остатке нуль. Последний неравный нулю остаток и есть НОД данных чисел.

Например: Найти НОД (273;1014).

Решение. Выполняем деление с остатком: По лемме:

1014=273*3+195

273=195*1+78

195=78*2+39

78=39*2

НОД (273;1014) = НОД(195;273) = НОД(195;78) = НОД(78;39)= 39

НОД(273;1014)=39

6 способ: Бинарный алгоритм Евклида нахождения наибольшего общего делителя (НОД)  двух натуральных чисел.

Данный алгоритм быстрее обычного алгоритма Евклида, т.к. вместо медленных операций деления и умножения используются сдвиги. Алгоритм был известен еще в Китае 1-го века, но опубликован был лишь в 1967 году израильским физиком и программистом Джозефом Стайном. Он основан на использовании следующих свойств НОД:

НОД(2a; 2b) = 2 НОД(a; b),

НОД(2a; 2b+1) = НОД(a; 2b+1),

НОД(-a; b) = НОД(a; b)

Сам алгоритм выглядит так:

1. Если a, b чётные, то НОД(a; b) = 2*НОД(a/2; b/2);

2. Если a чётное, b нечётное, то НОД(a; b) = НОД(a/2; b);

3. Если b чётное, a нечётное, то НОД(a; b) = НОД(a; b/2);

4. Если a, b нечётные и b > a, то НОД(a; b) = НОД((b-a)/2; a);

5. Если a, b нечётные и b < a, то НОД(a; b) = НОД((a-b)/2; b);

Например:

НОД(1978;2666)=2*НОД(989;1333)=2*НОД(989;344)=2*НОД(989;172)=2*НОД(989;86)=2*НОД(989;43)=2*НОД(946;43)=2*НОД(473;43)=2*НОД(430;43)= 2*НОД(215; 43)=2*НОД(172; 43)=2НОД*(86; 43)=2*НОД(43; 43)=2*43=86.

НОД(1978; 2666)=86

7 способ: Геометрический метод нахождения наибольшего общего делителя (НОД)  натуральных чисел с помощью квадратов.

Этот алгоритм – геометрическая иллюстрация алгоритма Евклида, описанного в 5-ем способе.

Например: Найти НОД(162;48).

Построим прямоугольник со сторонами 162мм и 48 мм.

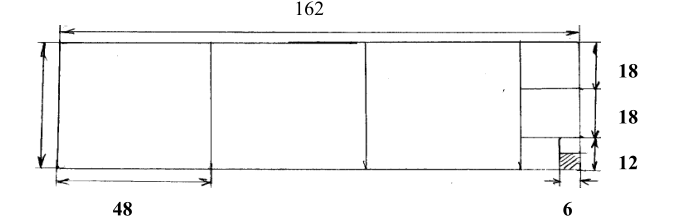
От прямоугольника отрежем несколько квадратов со стороной 48 мм – таких квадратов три.

Остался прямоугольник со сторонами 48 мм и 162-3*48=18 мм.

От полученного прямоугольника снова отрезаем квадраты, у которых сторона равна 18 мм – таких квадратов получится два.

Остался прямоугольник со сторонами 18 мм и 48-2*18=12 мм.

От полученного прямоугольника снова отрезаем квадраты, у которых сторона равна 12 мм – такой квадрат будет единственный.

Остался прямоугольник со сторонами 12 мм и 18-12=6 мм, который , в свою очередь состоит из двух квадратов 6мм х 6 мм.

Длина стороны последнего полученного квадрата и есть наибольший общий делитель чисел 162 и 48.

Ответ: НОД(162; 48)=6.

Этот способ мне кажется нерациональным: вычерчивая прямоугольники и квадраты, легко ошибиться в построениях и получится неверный ответ. Но все же я попробовал решить этим способом несколько примеров нахождения наибольшего общего делителя двух натуральных чисел (см. приложение 2).

4. Вывод работы

Во время работы над этим проектом я познакомился с различными способами нахождения НОД двух чисел. Выяснил, что нет идеального способа нахождения НОД двух чисел, у каждого из них есть достоинства и недостатки. Понял, что знания по этой теме позволяют экономить время, отводимое на выполнение работы, ведь теперь, в зависимости от того для каких чисел нужно будет найти НОД, я могу выбрать более рациональный способ. Может быть, мои знания по этой теме еще не велики. Но я понял самое главное, что при глубоком изучении данной темы мы получаем большие вычислительные навыки, навыки устного и быстрого счета, которые потом в дальнейшем пригодятся нам для решения более сложных задач математики, для решения практических задач, для успешной сдачи ЕГЭ.

Список используемой литературы:

1. Виленкин Н.Я. и др. Математика, 6 класс: учебник для общеобразовательных учреждений. – М.: Мнемозина, 2013.- 288с.

2. Макарычев Ю.Н., Миндюк Н.Г. Алгебра: Дополнительные главы к школьному учебнику 8 кл.: учебное пособие для школ и классов с углубленным изучением математики.- М.:Просвещение,1996.- 207 с.

3. Пичурин Л.Ф. За страницами учебника алгебры- Москва: Просвещение, 1990г. -

4. Щетников А. И. Алгоритм Евклида и непрерывные дроби. - Новосибирск: АНТ, 2003 г.

Список используемых источников информации:

1. Википедия (свободная энциклопедия), http://ru.wikipedia.org

2. Сайт "Единая коллекция цифровых образовательных ресурсов".

Приложение 1.

Мои примеры нахождения НОД двух натуральных чисел.

1способ: 1) НОД(81;243) 2) НОД(195;156)

D(81)={1,3,9,81} D(195)={1,3,5,15,65,195}

D(243)={1,3,9,27,81,243} D(156)={1,2,3,4,6,12,52,78,156}

НОД(81;243)=81 НОД(156;192)=3

__________________________________________________________________

2способ:

1)НОД(81;243) 2)НОД(195;156)

D(81)={1,3,9,27,81} D(156)={1,2,3,4,6,12,52,78,156}

81 является делителем 243 156 не является делителем 195

НОД(81;243)=81 78не является делителем 195

52 не является делителем 195

12 не является делителем 195

6 не является делителем 195

3 является делителем 195

НОД(195;156)=3

__________________________________________________________________

3 способ:1) НОД(585;360) 2) НОД(680,612)

585=13*3*3*5 612=17*2*2*3*3*3

360=2*2*3*3*5*2 680=17*2*2*2*5

5*3*3=45 17*2*2=68

НОД(585;360)=45 НОД(612;680)=68

__________________________________________________________________

4 способ:1) НОД(612,680) 2) НОД(585,360)

680-612=68 585-360=225

612-68=476 360-225=135

476-68=408 225-135=90

408-68=340 135-90=45

340-68=272 90-45=45

272-68=204 45-45=0

204-68=136 НОД(585,360)=45

136-68=68 3) НОД(100;2)

68-68=0 100-2=98

НОД(612,680)=68 98-2=96

96-2=94

94-2=92

……….

……….

……….

4-2=2

2-2=0

НОД(100;2)

Приложение 2.

Мои примеры нахождения НОД двух натуральных чисел.

5 способ: НОД(7875,4725) НОД(7920,594)

7875:4725=1(ост.3150) 7920:594=13(ост.153)

4725:3150=1(ост.1575) 594:153=3(ост.135)

3150:1575=2 153:135=1(ост.18)

НОД(7875,4725)=1575 135:18=7(ост.9)

18:9=2

НОД(7920,594)=9

__________________________________________________________________

6 способ: 1) НОД(825;675)

НОД(825;675) = НОД((825-675):2;675) = НОД((625-75) :2);75) =

НОД((275-75):2;75) = НОД((100:2);75) = НОД(50;75) = НОД(25;75) = 25 НОД(825;675)=25

2) НОД(7875;4725)

НОД(7875;4725)=НОД((7875-4725);2)=НОД(1575;4725)=НОД((4725-1575);2,1575)=НОД(1575;1575)=1575

НОД(7875;4725)=1575

7 способ: 1) НОД(160;40)

160мм

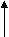
40

мм

1. Построим прямоугольник со сторонами 160мм и 40 мм.

2. От прямоугольника отрежем несколько квадратов со стороной 40 мм – таких квадратов четыре.

3. Длина стороны последнего полученного квадрата и есть наибольший общий делитель чисел 160 и 40.

НОД(160;40)=40

2) НОД(85,125)

1. Построим прямоугольник со сторонами 125мм и 85 мм.

5мм

40 мм

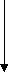
125 мм

2. От прямоугольника отрежем квадрат со стороной 85 мм – такой квадрат один.

3. Остался прямоугольник со сторонами 85 мм и 125-85=40 мм. От полученного прямоугольника снова отрезаем квадраты, у которых сторона равна 40 мм – таких квадратов получится два.

4. Остался прямоугольник со сторонами 40 мм и 85-2*40=5 мм. От полученного прямоугольника снова отрезаем квадраты, у которых сторона равна 8 мм – таких квадратов получится восемь.

5. Длина стороны последнего полученного квадрата и есть наибольший общий делитель чисел 125 и 8. НОД(85,125)=5