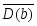
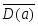
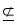
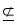
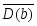
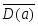
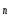
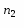
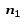
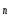
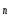
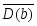
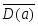
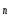
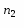
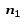
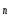
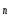
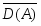
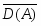
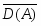
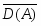
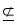
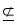
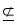
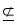
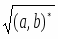
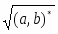
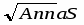
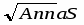
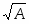
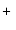
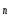
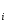
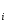
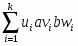
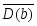
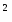
Министерство Образования Российской Федерации

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

«Редуцированные полукольца»

Работу выполнил студент

математического факультета

\Подпись\ ____________

Научный руководитель:

К.физ.-мат. наук

.

\Подпись\ ____________

Рецензент:

Д. физ.-мат. наук, профессор

.

\Подпись\ ____________

Допущен к защите в ГАК

Зав. кафедрой ___________________.

«___»________________

Декан факультета _______________.

«___»________________

Киров, 2003.

План.

1. Введение.

2. Основные понятия, леммы и предложения.

3. Доказательство основной теоремы.

1.Введение

Определение 1. Непустое множество S с бинарными операциями + и  называется полукольцом, если выполняются следующие аксиомы:

1. (S, +)  коммутативная полугруппа с нейтральным элементом 0;

2. (S, )  полугруппа с нейтральным элементом 1;

3. умножение дистрибутивно относительно сложения:

a(b + c) = ab + ac, (a + b)c = ac + bc

для любых a, b, c  S;

4. 0a = 0 = a0 для любого a S.

Итак, по принятому нами определению полукольцо отличается от ассоциативного кольца с единицей отсутствием операции вычитания и именно это вызывает основные трудности при работе с полукольцами.

В настоящей работе рассмотрен такой класс полуколец, как редуцированные полукольца.

Определение 2. Полукольцо S называется редуцированным, если для любых a, bS выполняется a = b, как только a+ b= ab + ba.

Целью данной работы является доказательство следующей теоремы.

Теорема . Для всякого редуцированного полукольца S равносильны следующие условия:

1. S слабо риккартово;

2.  a, bS (D(a)D(b)= =);

3. все идеалы Op, PSpec S, первичны(эквивалентно, вполне первичны, псевдопросты);

4. все идеалы OM, M Max S, первичны (эквивалентно, вполне первичны, псевдопросты) и P  M  Op=OM для  P Spec S и M Max S;

5. каждый первичный идеал полукольца S содержит единственный минимальный первичный идеал;

6.  a, b S (ab = 0  Ann a + Ann b = S);

Эта теорема обобщает факты, доказанные в классе колец ([1]).

2.Основные понятия, леммы и предложения

Для доказательства нашей теоремы нам потребуется определить некоторые понятия и вывести несколько фактов.

Определение 3. Полукольцо S называется симметрическим, если для любых элементов a, b, b, c  S выполняется

abc = abc  acb = acb.

Определение 4. Элемент aS называется нильпотентным, если в последовательности a, a, a,…, a, … встретится нуль.

Предложение 1. Редуцированное полукольцо S является симметрическим полукольцом без нильпотентов.

Доказательство: Пусть ab = ab. Тогда

baba = baba и baba = baba,

откуда

baba + baba = baba + baba

или иначе

(ba)+ (ba)= baba + baba.

В силу редуцированности ba = ba, т.е.

ab = ab  ba = ba. (1)

Аналогично доказывается ba = ba  ab = ab.

Пусть ab = ab. Тогда с помощью (1) ba = ba, откуда bac = bac и acb = acb. Значит, имеем:

ab = ab  acb = acb, ba = ba  bca = bca. (2)

Пусть сейчас abc = abc. Тогда

abc = abc  acbc = acbc  acbac = acbac  acbacb = acbacb и

acbacb = acbacb  (acb)+ (acb)= acbacb + acbacb  acb = acb.

Таким же образом доказывается другая импликация.

Пусть a+ b= ab + ba влечёт a = b. При b = 0 получаем a= 0  a = 0. Если с= 0 для некоторого натурального n  2, то c= 0 для k   с условием n  2. Получаем, что c= 0, и так далее. На некотором шаге получим c= 0, откуда с = 0. Предложение доказано.

Пример. Рассмотрим полукольцо S = {0, a, b, 1}, операции в котором заданы следующим образом:

+

a b 1

a

b

1

a b 1

b b b

1 b 1



a b 1

a

b

1

a a a

b b b

a b 1

Пример этого полукольца показывает, что, во-первых, в определении симметричности полукольца импликации нужны в обе стороны, поскольку aa = ab, но aa  ba. Во-вторых, S – полукольцо без нильпотентов, более того, без делителей нуля; однако симметрическим, в частности, редуцированным, оно не является. В этом проявляется отличие от колец, поскольку известно, что отсутствие нильпотентов в кольце влечёт кольцевую симметричность.

Определение 5. Собственный двусторонний идеал P полукольца S называется первичным, если AB  P влечёт A  P или B  P для любых идеалов A и B. Первичный идеал коммутативного полукольца называется простым.

Определение 6. Правый идеал P полукольца S называется псевдопростым, если ab = 0 влечёт a  P или b  P для a, b  S.

Предложение 2. Идеал P полукольца S первичен тогда и только тогда, когда для любых элементов a, b  S \ P найдётся элемент s  S такой, что asb  P. Если S  коммутативное полукольцо, то идеал P прост тогда и только тогда, когда a, b  P влечёт ab  P.

Доказательство: Пусть P первичен и элементы a, b  P. Тогда главные идеалы (a) и (b) не лежат в P, как и их произведение. Значит, некоторый элемент t  aSb не принадлежит P, поскольку t = для некоторых u,v,w S, то хотя бы для одного i  {1,…,k} a vb  P, ибо в противном случае каждое слагаемое uavbw лежит в P, и следовательно, t  P.

Обратно. Пусть произведение идеалов A и B лежит в P, но A P. Тогда найдётся a  A \ P. Предположим, что B P. Получим, что некоторый элемент b  B \ P и по условию asb  P для подходящего s S. Но тогда и AB P, и следовательно, P  первичный идеал.

Утверждение для коммутативного случая очевидно.

Определение 7. Подмножество T полукольца называется mсистемой, если 0 T, 1 T и для любых a, b  T найдётся такой s S, что asb  T.

Пример. Рассмотрим множество T = {a,a, a, … , a}, где n   и a  0. Оно является подмножеством полукольца Rнеотрицательных действительных чисел с обычными операциями сложения и умножения. 0  T, 1 T и для a,a T с = 1S : aсa= a T. Таким образом, T является mсистемой.

Легко увидеть, что если P – первичный идеал, то S \ P является m-системой. И хотя дополнение до mсистемы не обязано быть первичным идеалом, следующее утверждение показывает, что между ними существует глубокая связь.

Предложение 3. Пусть T  mсистема, а J  произвольный идеал полукольца S, не пересекающийся с T. Тогда любой максимальный идеал среди содержащих J и не пересекающихся с T первичен.

Доказательство: Пусть P  J, P  T =  и P  максимальный в семействе идеалов, удовлетворяющих этим условиям. Допустим, что aSb  P для некоторых a, b  P. Идеалы P + SaS и P + SbS строго содержат идеал P, и значит, пересекаются с T. Пусть m  (P + SaS)  T, r  (P + SbS)  T и msr  T для некоторого sS. Но, с другой стороны,

msr  (P + SaS)  (P + SbS)  P +SaSbS  P.

Получили противоречие, что P пересекается с T. Значит, предположение, что aSb  P неверно, и P  первичный идеал. Предложение доказано.

Определение 8. Собственный идеал M полукольца S называется максимальным идеалом, если M  A влечёт M = A или A = S для каждого идеала A.

Предложение 4. Максимальный идеал полукольца первичен.

Доказательство: Рассмотрим нулевой идеал J и не пересекающуюся с ним mсистему T = {1}. Любой максимальный идеал M полукольца содержит J и не пересекается с T, значит, по предложению 3 он будет первичным.

Определение 9. Для любого a  S множество

Ann aS = {t  S: (s  S) ast=0} называется аннулятором элемента a.

Ann aS является двусторонним идеалом полукольца S.

Ann a ={s  S: as = 0}  правый идеал и Ann aS  Ann a.

Определение 10. Для любого идеала P множество Op = {s  S: (tP) sSt = 0} = {s  S: Ann sS P} называется Oкомпонентой идеала P.

Лемма 1. Op является идеалом для любого первичного идеала P.

Доказательство: Пусть a, b  Op. Тогда aSt = 0 и bSu = 0 для некоторых t, u  P. В силу первичности P tsu  P для подходящего s  S. Для любого v  S

(a + b)vtsu = (avt)su + b(vts)u = 0.

Далее, (as)vt = a(sv)t = 0, (sa)vt = s(avt) = s0 = 0, поэтому a + b, sa, as  Op, и Op  идеал.

Лемма 2. Пусть P  M  первичные идеалы полукольца.

Тогда OM  Op  P.

Доказательство: Пусть a  OM, тогда aSt = 0 для некоторого t  M. Поскольку t  P, то a  Op, и значит, OM  Op. Для любого s  S 0 = ast  P. Поскольку P первичен, то a  P или t  P, отсюда a  P, и следовательно, Op  P.

Лемма 3. Для произвольных первичных идеалов P и P симметрического полукольца S верна импликация:

P  P не содержит первичных идеалов  Op P.

Доказательство: Предположим, что Op  P. Полагая A = S \ P и B = S \ P, рассмотрим множество AB всевозможных конечных произведений элементов из A  B. Покажем, что AB  Op = . В самом деле, если s  AB  Op, то sb = 0 для некоторого b  A, т.е. {0}  AB. Поскольку s является произведением элементов из A  B, то в силу первичности идеалов P и P и свойства симметрических полуколец uv = 0 для подходящих u  B, v  A. Откуда u  Op P  противоречие.

Таким образом, AB является mсистемой, и значит, существует первичный идеал Q, не пересекающийся с AB и содержащий Op. А так как A  B  AB, то P  P  Q. Получили противоречие с условием, значит наше предположение неверно, и Op P.

Следствие 1. Для произвольных первичных идеалов P и P в симметрическом полукольце, если Op  P , то пересечение P и P содержит хотя бы один первичный идеал.

Определим множество (a, b) = {s  S: xS (axs = bxs)}  идеал полукольца S для a, b  S.Очевидно, (a, 0) = Ann aS.

Для произвольного идеала A обозначим  пересечение первичных идеалов полукольца S, содержащие идеал A.

Определение 11. Полукольцо S называется строго полупервичным, если для любых элементов a, b  S выполняется

= (a, b).

Определение 12. Пересечение rad S всевозможных первичных идеалов в S называется первичным радикалом полукольца S.

Определение 13. Полукольцо называется полупервичным, если его первичный радикал равен нулю.

Предложение 5. Полукольцо S полупервично тогда и только тогда, когда = Ann aS для всех a  S.

Доказательство: При a = 1 rad S = = Ann S = 0, т.е. S  полупервично.

Пусть S  полупервичное полукольцо и b . Для каждого первичного идеала P, либо P содержит Ann aS, либо Ann aS не содержится в P. В первом случае b  P, во втором случае a  Op  P. Тогда aSb rad S = 0, откуда b  Ann aS. Следовательно,  Ann aS. Другое включение справедливо всегда.

Следствие 2. Строго полупервичное полукольцо является полупервичным.

Предложение 6. Всякое редуцированное полукольцо S строго полупервично.

Доказательство: Пусть c (a, b) для a, b  S. Тогда ac  bc и из редуцированности S вытекает, что acac + bcbc  acbc + bcac. Элементы cac и cbc отличны друг от друга, и значит, ac bc в силу симметричности редуцированного полукольца. Аналогично ac bc, и следовательно, ac bc. По индукции ac  bc. Значит, T = {1, c, c,…}  mсистема, не пересекающаяся с (a, b), и поэтому найдётся первичный идеал P, содержащий (a, b), при этом c  S \ P. Значит, c , откуда  (a, b). Другое включение справедливо всегда.

Получили = (a, b)  по определению 12 S  строго полупервично, что и требовалось доказать.

Обозначим через Spec S множество всех первичных идеалов полукольца S. Для любого идеала A полукольца S положим

D(A) = {P  Spec S: A P}.

Множество D({0}) = {P  Spec S: {0}P} = , а Spec S = D(S).

D(A)  D(B) = { P  Spec S: A P  B P} = { P  Spec S : AB P} = D(AB).

Spec S является топологическим пространством с семейством открытых множеств вида D(A).

Лемма 4. Для любого идеала A полупервичного полукольца S

= {P  Spec S: Ann A  P}.

Доказательство: Обозначим через Y правую часть доказываемого равенства. Если P  D(A), т.е. A P, то Ann A  P, т.е. P  Y. Откуда  Y, ибо Y замкнуто.

Обратно, пусть P . Тогда P лежит в некоторой окрестности D(B), где B  некоторый идеал в S, не пересекающийся с.

D(A)  D(B) = , тогда AB  rad S = 0, т.е. B  Ann A.

Тогда P не содержит Ann A , иначе P содержал бы B . Следовательно, P  Y . Получили Y  .

Лемма 5. Пусть P  первичный идеал редуцированного полукольца S. Тогда P = Op  P  минимальный первичный идеал.

Доказательство: Пусть P = Op , P  Spec S и P   P. Тогда Op  OP  P . Поэтому P = P, и P минимален.

Обратно, пусть дан минимальный первичный идеал P редуцированного полукольца S. Предположим, что существует a P \ Op. Степени элемента a образуют mсистему (0 {a}, 1{a} и для a,a{ a} с = 1S : aсa= a{ a}),не пересекающуюся с Op. Действительно, если a Op , n  , то ab = 0 для некоторого b S \ P. Но тогда (ab)= 0, так как редуцированное полукольцо симметрическое без нильпотентов, и значит ab = 0, то есть a  Op ;противоречие. Из предложения 3 видно, что найдётся идеал P  Op, не содержащий a, который будет первичным. Из следствия 1 вытекает, что в S существует первичный идеал, лежащий в P  P ,что противоречит минимальности P. Значит, P  Op. Также Op  P (Лемма 2). Тогда P = Op.

Лемма 6. Любой первичный правый идеал симметрического полукольца псевдопрост.

Доказательство: В самом деле, если a, b  S \ P, то asb  P для подходящего s  S, откуда asb  0 и ab  0.

Определение 14. S – слабо риккартово  a  S b  Ann aS

Ann aS + Ann b = S

Пример. Обозначим через N – полукольцо всех неотрицательных целых чисел с обычными операциями сложения и умножения. Возьмём a = 0 N. Тогда Ann aS = N. В результате получим, что Ann aS + Ann b = N. Теперь возьмём a  N \ {0}. Тогда Ann aS = {0}, а Ann b = N. В результате получим, что Ann aS + Ann b = {0} + N = N . Таким образом, N – слабо риккартово полукольцо. Аналогично, любое полукольцо без делителей нуля будет являться слабо риккартовым.

3. Доказательство основной теоремы.

Теорема . Для всякого редуцированного полукольца S равносильны следующие условия:

1. S слабо риккартово;

2.  a, bS (D(a)D(b)= =);

3. все идеалы Op, PSpec S, первичны(эквивалентно, вполне первичны, псевдопросты);

4. все идеалы OM, M Max S, первичны (эквивалентно, вполне первичны, псевдопросты) и P  M  Op=OM для  P Spec S и M Max S;

5. каждый первичный идеал полукольца S содержит единственный минимальный первичный идеал;

6.  a, b S (ab = 0  Ann a + Ann b = S);

Доказательство: Пусть S  редуцированное полукольцо. Такое S  симметрическое (по предложению 1), поэтому S обладает всеми свойствами симметрических полуколец. Доказательство проведём по схеме 1)3)4)5)6)1) и 2)6).

1)3). Исходя из 1), покажем, что каждый идеал Op вполне первичен. Пусть P  Spec S и ab Op при a, b  S.

Тогда  сS \ P: abSc = 0,т.е. absc = 0 для  s  S.

Возьмём s = 1  abc = 0  bc  Ann aS (по определению Ann aS). Но Ann aS  Ann a . Тогда bc Ann a. По условию 1) S  слабо риккартово, т.е. Ann aS + Ann bc = S для a S, bc  Ann aS.

 e Ann aS, f Ann bc: e + f = 1 (1S).

Предположим, что a Op  Ann aS  P (по определению Ann aS)  e P.

Тогда f P, т.к. в противном случае 1P. Но P  первичный идеал  P  собственный  1P.

f Ann bc  bcf = 0. Т.к. S  симметрическое  bScf = 0. Но cf P (т.к. c P, f P , а P  первичный идеал)  b  Op .

Таким образом, получили, что все идеалы Op , P  Spec S, вполне первичны.

3)4). По условию 3 все идеалы Op , где P  Spec S, первичны. Но M  Max S – является первичным идеалом (предложение 4), т.е. M  Spec S. Но тогда по условию 3) данной теоремы следует, что все идеалы OM , где M  Spec S и M  Max S, первичны.

Пусть P  M. Тогда OM  Op (лемма 2).

Если a  Op , т.е. ab = 0 при некотором b S \ P и s = 1S, то a OM , ибо b OM  P, а ab = 0 OM и OM псевдопрост (доказано выше). Значит и Op  OM . Тогда Op = OM .

4)5). Пусть P – первичный идеал из S и P  M. По условию 4) данной теоремы OM – первичный идеал и так как P  M  Op = OM . Также Op  P (Лемма 2). Докажем, что OM – минимальный первичный идеал в S, лежащий в P. Пусть в P лежит Q  минимальный первичный идеал полукольца S. Но Q  M  OM  OQ  Q. По условию 4) данной теоремы OM = OQ. . Так как Q – минимальный первичный идеал  OQ = Q (Лемма 5). По свойству транзитивности равенства получаем, что Op = OM =Q.

Докажем теперь единственность такого первичного идеала. Пусть P   произвольный минимальный первичный идеал в S, отличный от Q и лежащий в M. Тогда OP = OM (по условию 4)). Также OP = P  .

Тогда получили равенство Q = OQ = OM = OP = P  . Единственность доказана.

Так как все первичные идеалы полукольца S содержатся в M Max S, то мы получили, что каждый первичный идеал полукольца S содержит единственный минимальный первичный идеал.

5)6). Пусть ab = 0, но Ann a + Ann b  S для некоторых a, b S.

Тогда Ann a + Ann b  M для подходящего M  Max S.

Рассмотрим единственный минимальный первичный идеал P, содержащийся в M. Тогда OM  P (Лемма 2). Предположим, что a  P \ OM . Степени элемента a образуют mсистему (0 {a}, 1{a} и для a,a{ a} с = 1S: aсa= a{ a}),не пересекающуюся с OM. Действительно, если a OM, n  , то ab = 0 для некоторого b S \ M. Но тогда (ab)= 0, так как редуцированное полукольцо симметрическое и значит ab = 0, то есть a OM ; противоречие. Из предложения 3 видно, что найдётся идеал P  OM, не содержащий a, который будет первичным.

Пусть q, w  S \ P и q, w  S \ P . Тогда s  S: qsw  P  qsw  P  P   P  P  первичный идеал, что противоречит минимальности P. Значит P  OM и P = OM. Первичный идеал OM псевдопрост, поэтому aOM или b OM. Откуда по определению нулькомпонент Ann a M  Ann bM  Ann a + Ann b M  противоречие  Ann a + Ann b = S.

6)1). Возьмём a, b S: ab = 0  b  Ann aS.

Из условия 6) данной теоремы вытекает равенство:

Ann a + Ann b = S. Так как в симметрическом полукольце Ann aS = Ann a, то Ann aS + Ann b = S. Таким образом, полукольцо Sслабо риккартово, что и требовалось доказать.

2)6). Пусть a, b  S и ab = 0. D(a)  D(b) = {PSpec S: aP  bP} = { PSpec S: ab  P} (в силу первичности) = D(ab) = D(0) = .

Обратно, D(a)  D(b) ={PSpec S: aP  bP} ={PSpec S: ab  P}=D(ab) =  ab = 0, так как D(x) =   x = 0.

Таким образом, ab = 0  D(a)  D(b) = .

Так как S – симметрическое полукольцо на основании предложения 1, то к нему можно применить предложение 6, то есть S строго полупервично. По следствию 2 S является и полупервичным. Теперь мы можем применить лемму 4. На основании этой леммы

= {SSpec S: Ann aP  Ann bP} = .

Тогда Ann a + Ann b M для  M  Max S  Spec S  Ann a + Ann b = S.

В другую сторону, пусть Ann a + Ann b = S  Ann aM  Ann bM для подходящего M  Max S  Spec S.

Тогда = {S  Spec S: Ann a P  Ann b P} = . Таким образом, условия 2) и 6) равносильны.

Теорема доказана полностью.

Cвойство:

Если редуцированное полукольцо S слабо риккартово, то для любого правого идеала A и элементов a, b полукольца S выполняется импликация:

ab = 0 и a + b  A  a  A.

Доказательство: Пусть даны в S правый идеал A и такие элементы a и b, что ab = 0 и a + b A. Так как условие 6) доказанной теоремы равносильно тому, что S слабо риккартово, то мы можем доказать это свойство, исходя из него. Тогда Ann a + Ann b = S, то есть c + k = 1 при некоторых c Ann a и k Ann b.

c  Ann a  ac = 0 (по определению аннулятора).

k  Ann b  bk = 0.

a = a1 + 0 = a(c + k) + bk = ac + ak + bk = ac + (a + b)k = (a + b)k A.

Получили a A, что и нужно было доказать.

Литература.

1. Е.М. Вечтомов. «Функциональные представления колец». – М.: МПГУ им. Ленина, 1993. – 190 с.

2. В.В.Чермных. «Полукольца». Киров: Изд-во ВГПУ, 1997.  131 с.