Регрессионный анализ корелляции субъективного ВАШ и лабораторных признаков активности реактивного
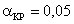
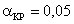
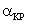
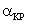
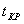
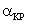
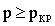



 Санкт-Петербургский Государственный Университет
Санкт-Петербургский Государственный Университет
Факультет прикладной математики – процессов управления
Кафедра диагностики функциональных систем
Варламова Александра Александровна
Регрессионный анализ корелляции субъективного ВАШ и лабораторных признаков активности реактивного артрита
Заведующий кафедрой
доктор медицинских наук, профессор Шишкин В.И.
Научный руководитель
доктор медицинских наук, профессор Шишкин В.И.
Санкт-Петербург
2008
Содержание
Введение
Артриты реактивные - термин, принятый для обозначения артритов, развивающихся после инфекций, но не обусловленных попаданием инфекционного агента в полость сустава. Обычно реактивные артриты носят иммунокомплексный характер, т. е. возникают вследствие нарушений иммунитета у генетически предрасположенных лиц из-за недостаточной утилизации комплексов антиген - антитела макрофагальной системой. Реактивные артриты могут развиваться после многих инфекций (бактериальных, вирусных и др. ) независимо от их тяжести, но чаще - после энтероколитов, вызванных иерсиниями, и инфекций мочевых путей, обусловленных хламидиями.
В настоящее время реактивный артрит (РеА) является одним из наиболее частых ревматологических диагнозов. Обычно реактивным считают артрит, который не удовлетворяет диагностическим критериям ревматоидного или подагрического артрита и не сопровождается специфической для системных ревматических заболеваний внесуставной симптоматикой.
Этиология РеА неизвестна. Предположительно, в основе РеА лежит генетически детерминированная аномалия иммунной системы, которая реализуется при инфицировании некоторыми микроорганизмами.
Клиническая картина РеА может включать:
• характерный суставной синдром;
• клинику урогенитальной инфекции;
• внесуставные поражения (кожи и слизистых оболочек);
• поражения позвоночника (обычно сакроилеит);
• висцеральные поражения;
• системную воспалительную реакцию
Суставной синдром (обязательное проявление заболевания) характеризуется:
– асимметричным олигоартритом (воспалением 2-3 суставов или суставных групп) с поражением суставов ног (коленных, голеностопных, плюснефаланговых и межфаланговых) и тендовагинитом (ахиллобурситом);
– началом первого эпизода артрита в период до 30 дней после полового контакта, со средним интервалом в 14 дней между появлением урогенитальных симптомов и артритом;
– болью и ригидностью с отеком или без него в области прикрепления мышц, сухожилий и связок, особенно ахиллова сухожилия и плантарной фасции, к пяточной кости, что часто ведет к затруднениям при ходьбе
Клинические признаки артрита :
1. Боль в суставе/суставах:
• ощущается во всем суставе;
• связана с движениями и суточным ритмом (при любых движениях, усиливается в покое и ночью);
• сопряжена с амплитудой движений в суставе (при движениях во всех плоскостях, нарастающая с увеличением амплитуды движений);
• обычно тупая, ноющая, выкручивающая.
2. Скованность – субъективное ощущение препятствия движению, которое, как правило, наиболее выражено сразу после пробуждения, периода отдыха или неактивности. Скованность обусловлена нарушением оттока жидкости из воспаленного сустава в покое, уменьшается или проходит при возобновлении движений в суставе. Продолжительность и выраженность скованности отражают степень местного воспаления.
3. Припухлость – преходящее увеличение в размерах и изменение контура сустава, обусловленные как накоплением экссудата в полости сустава, так и отеком периартикулярных тканей. Наиболее отчетливо припухлость выявляется на разгибательных (тыльных) поверхностях локтевых и лучезапястных суставов, на кисти, коленных и голеностопных суставах и стопе.
4. Повышение температуры суставов также является признаком воспаления. Определяется проведением тыльной стороной ладони по поверхности сустава.
5. Болезненность сустава при пальпации подтверждает, что боль в суставе обусловлена именно его поражением, а не является отраженной.
Системная воспалительная реакция
Системные симптомы недомогания, усталости, потеря веса и лихорадка встречаются примерно у 10% пациентов. Практические у всех больных в клиническом анализе крови повышена скорость оседания эритроцитов (СОЭ).
Объект, предмет, цель и задача исследования
В качестве исходных данных для исследования даны выборки численных значений медико-биологических показателей человеческого организма, а именно, показатели активности заболевания : СОЭ, наличие С-реактивного белка, уровня фибриногена и гемоглобина в крови больных реактивным артритом. А также выборка значений болевого синдрома оцененного в баллах по визуальной аналоговой шкале (ВАШБП) и синдрома припухлости (ВАШСП).
В целях полноты изложения приведем необходимые определения :
СОЭ (скорость оседания эритроцитов) - свойство эритроцитов оседать при помещении несвернувшейся крови в вертикально поставленную пробирку. Ускорение наблюдается при большинстве воспалительных, инфекционных и др. заболеваниях.
С-реактивный белок (СРБ) очень чувствительный элемент крови, быстрее других реагирующий на повреждения тканей. Наличие реактивного белка в сыворотке крови – признак воспалительного процесса, травмы, проникновения в организм чужеродных микроорганизмов – бактерий, паразитов, грибов. С-реактивный белок стимулирует защитные реакции, активизирует иммунитет. Определение СБР используется для диагностики острых инфекционных заболеваний и опухолей. Также анализ СРБ используется для контроля над процессом лечения, эффективности антибактериальной терапии и т.д.
Гемоглобин (от гемо... и латинское globus - шар), красный дыхательный пигмент крови человека, позвоночных и некоторых беспозвоночных животных. Состоит из белка (глобина) и железопорфирина - гема. Переносит кислород от органов дыхания к тканям и диоксид углерода от тканей к дыхательным органам. Многие заболевания крови (анемии) связаны с нарушениями строения глобина, в том числе наследственными (гемоглобинопатии - серповидноклеточная анемия, талассемия и др.).
Фибриноген (от фибрин и ...ген), растворимый белок плазмы крови, относящийся к группе глобулинов; фактор I свёртывания крови, способный под действием фермента тромбина превращаться в фибрин. Молекула имеет форму глобулы диаметром около 22 нм. Синтез фибриногена в организме происходит в паренхиматозных клетках печени. Содержание фибриногена в плазме крови здорового человека 300- 500 мг%. При недостаточности фибриногена в организме или при образовании молекул с аномальным строением наблюдается кровоточивость.
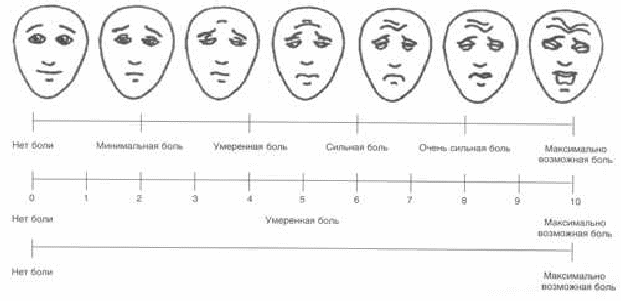
ВАШБП - оценка интенсивности боли, для характеристики которой используют простые визуальные аналоговые шкалы.
ВАШСП – оценка припухлости суставов, для характеристики которой используют простые визуальные аналоговые шкалы
Визуально аналоговые шкалы важный компонент большинства современных клинических методов, применяемых при обследовании пациентов. Специальные опросники позволяют дать более полную характеристику болевого синдрома, выявить связь между выраженностью боли и нарушением функционального состояния больных.
Объект исследования
Объектом нашего исследования являются выборочные данные результатов измерений СОЭ, СРБ, Гемоглобина, Фибриногена, ВАШБП и ВАШСП, причем изучаемые данные разделены на 4 группы. В первой группе представлены данные при болезни, вызванной моче половыми инфекциями, во второй группе - неизвестной этиологии, в третьей – ОРВИ, в четвертой – желудочно-кишечными инфекциями.
Предмет исследования
Предмет исследования определяем, как нахождение зависимости между показателями активности заболевания (СОЭ, СРБ, Фибриноген, Гемоглобин), болевым синдромом оцененным по визуально аналоговой шкале (ВАШБП) и синдромом припухлости оцененным также по визуально аналоговой шкале (ВАШСП).
Используемые методы
1.Дисперсионный анализ по одному признаку для проверки равенства нескольких средних
Во многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак. В данном случае фактором является вид инфекции вызвавший реактивный артрит, а признаками СОЭ, СРБ, Фибриноген, гемоглобин, ВАШБП и ВАШСП. Научное обоснованное решение подобной задачи при некоторых предположениях составляет предмет дисперсионного анализа.
Статистическая модель
Выборки производятся из нормальных совокупностей. Первая выборка производиться из совокупности со средним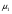 , вторая - со средним
, вторая - со средним 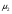 , k-я из совокупности со средним
, k-я из совокупности со средним 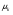 . Все наблюдения независимы.
. Все наблюдения независимы.
Критическая область.
Если значение p0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выберем критический уровень значимости pKP для условия принятия нулевой гипотезы pкр=0,05
p>pкр
Гипотезы №1.
Н0 : 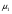 =
= 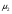 =…=
=…= 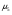
Н1: не все средние равны.
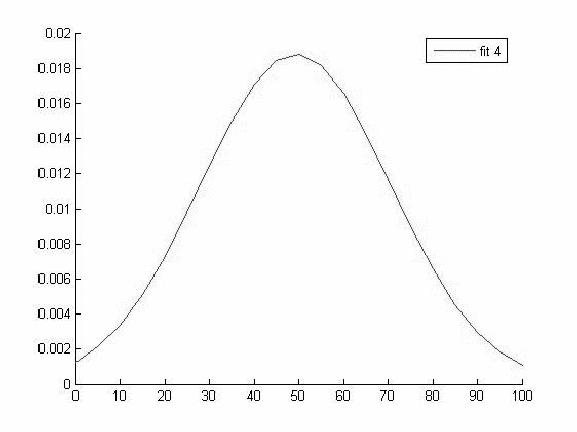
Так как данный метод работает только для нормальных совокупностей то сначала построим графики функций распределения для каждой выборки.
Для экономии времени и упрощения расчетов воспользуемся Matlab.
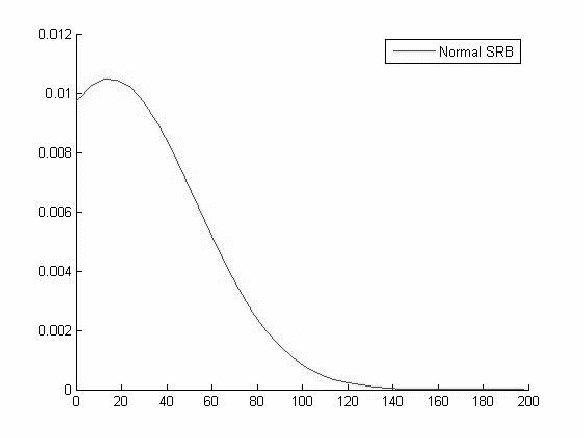
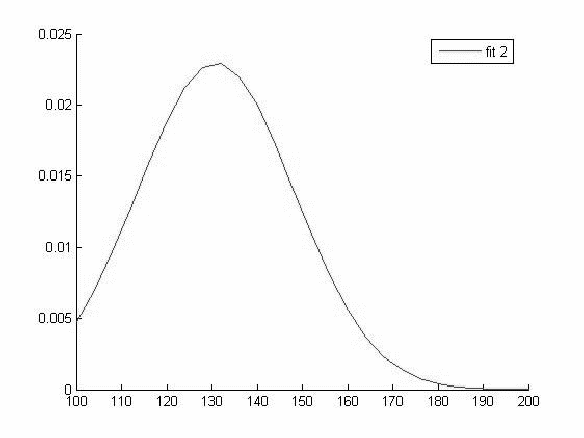
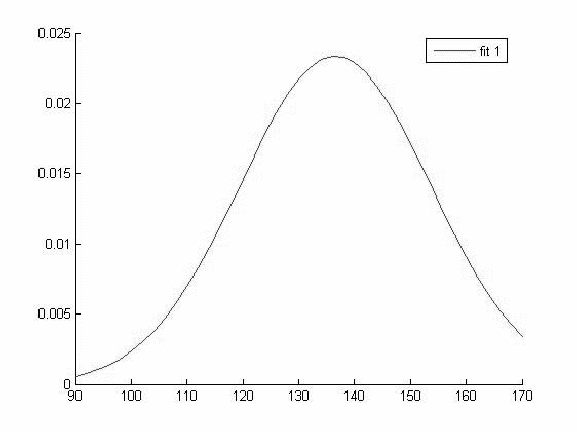
График функции распределения для значений Hb в 1 группе
График функции распределения для значений Hb в 2 группе
График функции распределения для значений Hb в 3 группе
График функции распределения для значений Hb в 4 группе
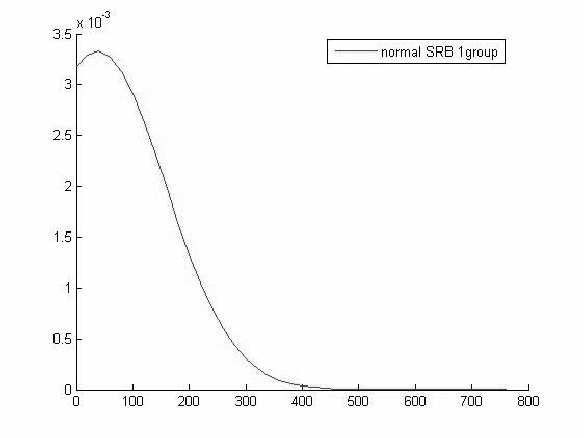
График функции распределения для значений СРБ в 1 группе
График функции распределения для значений СРБ в 2 группе
График функции распределения для значений СРБ в 3 группе
График функции распределения для значений СРБ в 4 группе
График функции распределения для значений СОЭ в 1 группе
График функции распределения для значений СОЭ в 2 группе
График функции распределения для значений СОЭ в 3 группе
График функции распределения для значений СОЭ в 4 группе
График функции распределения для значений Фибриногена в 1 группе
График функции распределения для значений Фибриногена в 2 группе
График функции распределения для значений Фибриногена в 3 группе
График функции распределения для значений Фибриногена в 4 группе
График функции распределения для значений ВАШБП в 1 группе
График функции распределения для значений ВАШБП в 2 группе
График функции распределения для значений ВАШБП в 3 группе
График функции распределения для значений ВАШБП в 4 группе
График функции распределения для значений ВАШСП в 1 группе
График функции распределения для значений ВАШСП в 2 группе
График функции распределения для значений ВАШСП в 3 группе
График функции распределения для значений ВАШСП в 4 группе
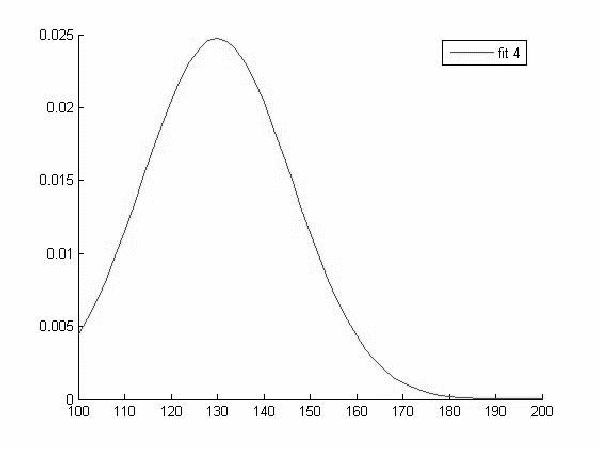
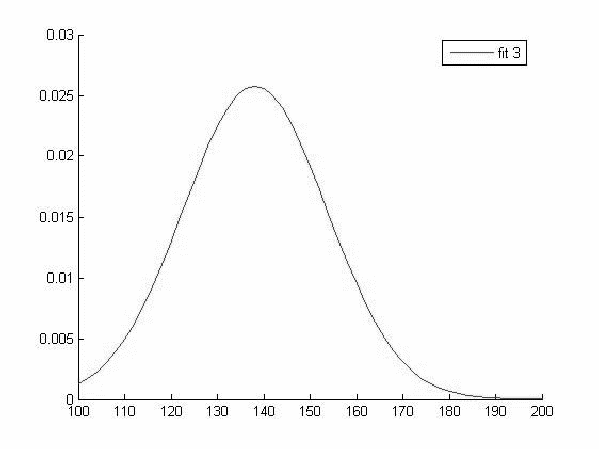
Исходя из вида графиков можно сделать вывод о том что все выборки имеют нормальное распределение и следовательно мы можем использовать выбранный нами параметрический метод дисперсионного анализа.
I) Рассмотрим сначала влияние фактора на уровень Hb (гемоглобин):
Таблица1.1.1.Зависимость уровня Hb от инфекции вызвавшей заболевание
1группа
2группа
3 группа
4группа
124
114
140
124
124
142
121
130
110
156
136
127
93
170
125
130
133
119
138
138
129
128
150
122
149
163
154
160
122
135
127
104
145
120
153
121
124
120
120
131
99
106
171
127
125
130
128
109
137
156
154
158
156
114
140
132
148
137
110
134
138
142
151
164
144
121
142
116
133
121
144
136
145
144
120
122
121
160
150
126
140
112
128
110
124
120
135
137
150
106
130
123
126
160
150
136
150
160
142
107
139
118
114
152
126
124
146
140
120
142
101
115
137
123
148
117
130
152
126
118
140
166
128
165
143
132
130
126
166
168
128
126
125
115
118
117
114
123
150
125
103
142
150
140
94
129
156
141
148
140
141
135
150
150
127
158
131
150
162
134
104
130
136
150
136
105
146
146
138
158
154
141
134
150
150
114
109
157
161
133
166
168
Здесь и далее для экономии времени и упрощения вычислительн6ой работы воспользуемся Matlab для проведения однофакторного дисперсионного анализа для сравнения средних арифметических значений выборок. Будем использовать функцию p = anova1(X) - функция позволяет провести однофакторный дисперсионный анализ для сравнения средних арифметических значений одной или нескольких выборок одинакового объема. Выборки определяются входным аргументом Х. Х задается как матрица с размерностью mxn, где m - число наблюдений в выборке (число строк Х), n - количество выборок (число столбцов матрицы Х). Выходным аргументом функции является уровень значимости p нулевой гипотезы. Нулевая гипотеза состоит в том, что все выборки в матрице Х взяты из одной генеральной совокупности или из разных генеральных совокупностей с равными средними арифметическими. p является вероятностью ошибки первого рода, или вероятностью необоснованно отвергнуть нулевую гипотезу. Если значение p0, то нулевая гипотеза может быть отвергнута, т.е. хотя бы одно среднее арифметическое отличается от остальных значений. Выбор критического уровня значимости pKP для условия принятия нулевой гипотезы
предоставлен исследователю. Здесь и далее примем pKP равным 0,05.
После выполнения вычислений мы получаем:
p = 0.3001
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №1.1.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
1012,4
3
337,451
Остаточная
30577,2
112
273,011
Полная
31589,5
115
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень гемоглобина в крови не зависит от инфекции вызывающей реактивный артрит.
II) Влияние фактора на наличие СРБ в крови
Таблица1.2.1.Зависимость уровня СРБ от инфекции вызвавшей заболевание
1 группа
2 группа
3 группа
4 группа
0
6
0
0
6
0
0
0
96
48
0
0
192
0
0
0
0
6
12
96
0
6
12
0
0
0
6
0
0
12
0
0
0
0
0
48
0
0
48
0
48
192
0
384
0
0
0
48
12
6
0
0
0
48
0
0
384
6
12
0
192
0
0
0
12
0
0
0
48
0
48
0
0
0
0
0
96
0
0
0
0
0
48
0
96
0
0
96
12
48
48
6
0
0
6
0
0
0
0
0
96
0
0
48
0
48
6
0
48
0
12
0
0
96
0
0
0
0
0
768
96
0
0
0
0
0
12
0
0
6
0
6
0
0
0
0
6
0
0
192
48
0
0
192
768
6
0
96
24
0
6
0
0
0
0
0
0
0
0
0
0
0
0
0
96
48
0
0
48
0
0
6
0
0
0
0
0
0
0
0
0
0
После выполнения вычислений мы получаем:
p =0.4677
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №1.2.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
23192,8
3
7730,92
Остаточная
1616980,7
178
9084,16
Полная
1640173,5
181
-----
p>pкр
Вывод:
Следовательно, мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень СРБ в крови не зависит от инфекции вызывающей реактивный артрит.
III) Влияние фактора на СОЭ
Таблица1.3.1.Зависимость СОЭ от инфекции вызвавшей заболевание
1 группа
2 группа
3 группа
4 группа
18
34
10
10
19
4
21
26
42
24
3
6
66
1
7
4
25
35
22
12
10
16
26
25
13
1
12
4
28
36
6
40
3
22
1
52
26
34
18
18
28
50
1
62
38
28
2
40
28
14
4
7
1
64
10
5
52
30
23
3
48
9
2
8
26
32
10
12
14
10
17
5
12
2
15
12
48
2
12
19
12
10
28
37
30
25
18
24
6
58
40
11
10
2
26
15
2
2
2
8
51
10
5
24
10
10
13
10
35
6
34
39
10
38
2
25
30
2
3
46
56
3
11
4
4
24
11
7
1
7
9
20
14
4
12
17
14
5
2
40
30
6
3
26
69
25
3
35
6
8
3
5
1
5
5
7
6
3
3
5
10
15
3
3
38
49
5
3
19
2
3
10
5
3
5
16
5
4
4
10
1
4
После вычислений получаем:
p = 0.0810
Таблица №1.3.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
1658,2
3
552,744
Остаточная
43145,7
178
242,391
Полная
44803,9
181
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости СОЭ не зависит от инфекции вызывающей реактивный артрит.
IV) Влияние фактора на уровень Фибриногена в крови
Таблица1.4.1.Зависимость уровня фибриногена от инфекции вызвавшей заболевание
1 группа
2 группа
3 группа
4 группа
3.00
5.25
6.75
2.80
4.50
2.00
2.50
3.75
3.50
5.75
3.10
2.50
7.25
2.50
3.00
3.00
4.00
5.50
6.75
3.25
3.25
3.50
4.50
3.50
5.50
3.25
3.50
3.75
4.00
7.25
2.50
5.25
3.25
3.75
2.50
5.10
5.00
3.00
4.50
4.50
3.60
7.00
3.00
12.20
4.25
5.50
2.15
5.75
4.25
4.00
2.00
5.50
3.00
7.50
3.25
3.00
10.20
3.50
4.25
2.50
4.75
4.00
2.25
3.00
4.50
5.50
2.10
3.50
5.00
3.25
4.75
3.00
5.50
2.50
3.50
2.00
5.50
3.00
3.50
3.75
3.50
4.00
3.75
5.00
3.50
4.50
3.30
3.00
5.75
5.00
2.75
3.00
4.25
3.00
4.25
3.00
2.75
3.75
2.00
3.00
5.25
3.25
2.00
6.25
2.50
1.75
2.25
3.25
4.25
3.25
4.30
3.00
2.50
4.25
2.75
4.00
4.00
2.75
4.00
4.50
6.75
3.25
3.75
3.25
4.00
4.25
3.50
2.60
2.75
4.25
2.00
3.75
4.00
4.00
3.00
4.00
3.00
3.20
2.00
8.75
4.00
4.00
5.00
5.00
7.50
4.00
3.25
2.90
3.25
2.90
3.00
2.00
3.00
2.00
2.75
3.00
2.93
4.25
3.00
3.75
4.00
3.00
2.75
2.00
6.00
3.50
3.00
2.50
4.75
3.00
2.75
3.25
2.50
2.00
3.10
2.00
3.25
3.25
3.00
3.25
3.25
4.00
После вычислений получаем:
p =0.5494
Таблица №1.4.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
4.733
3
1.57754
Остаточная
397.546
178
2.2334
Полная
402.278
181
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости уровень фибриногена в крови не зависит от инфекции вызывающей реактивный артрит.
V) Влияние фактора на показатель ВАШБП
Таблица 1.5.1.Зависимость ВАШБП от инфекции вызвавшей заболевание
1 группа
2 группа
3 группа
4 группа
15
25
45
67
28
25
57
65
63
35
40
50
45
33
33
45
40
65
55
55
80
45
50
27
20
50
55
58
48
25
40
45
75
45
0
30
35
44
45
50
55
100
48
35
85
65
30
20
45
55
25
78
43
64
20
50
45
15
40
60
50
15
20
75
50
40
13
75
56
28
30
30
10
15
5
55
55
25
15
45
17
30
95
70
20
32
45
40
25
55
35
70
40
35
45
10
15
28
5
55
27
25
30
75
10
25
45
2
16
55
35
30
35
60
33
45
5
45
35
73
55
56
43
55
20
53
30
55
55
15
70
60
36
20
38
15
53
12
23
40
52
25
0
70
95
25
10
27
40
20
45
15
17
25
25
10
35
70
12
5
38
5
0
5
65
57
5
0
25
5
20
21
5
10
15
15
23
35
3
10
37
После вычислений получаем:
p = 0.4569
Таблица №1.5.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
1210.5
3
403.498
Остаточная
82391
178
462.871
Полная
83601.5
181
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШБП не зависит от инфекции вызывающей реактивный артрит.
VI) Влияние фактора на показатель ВАШСП
Таблица 1.6.1.Зависимость ВАШСП от инфекции вызвавшей заболевание
1 группа
2группа
3группа
4группа
20
35
62
70
53
32
70
78
68
28
40
41
55
40
50
30
43
65
60
60
75
25
56
40
12
70
68
60
40
38
20
42
67
52
10
83
38
40
40
53
80
100
70
70
80
55
50
51
41
50
34
70
65
78
30
80
50
15
32
70
48
38
25
80
45
50
20
75
50
28
39
30
25
30
10
19
40
35
10
55
29
31
89
68
60
60
45
45
25
70
45
70
50
39
50
10
15
50
20
50
55
35
20
55
20
20
60
2
50
55
37
40
40
55
32
50
40
54
47
80
78
65
50
62
25
52
50
30
60
19
70
70
41
30
43
17
60
15
20
41
43
40
5
80
95
35
20
35
40
48
18
18
40
60
10
20
12
10
50
3
0
5
63
58
10
0
80
10
30
20
5
9
10
40
20
33
5
18
40
15
После вычислений получаем:
p = 0.3222
Таблица №1.6.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
1701.7
3
567.223
Остаточная
85230.9
176
484.266
Полная
86932.5
179
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу. т.е. можно предположить что при 5% уровне значимости ВАШСП не зависит от инфекции вызывающей реактивный артрит.
В связи с тем что не один из показателей активности заболевания а также показатели ВАШ не зависят от инфекции предшествующей реактивному артриту дальнейшее разделение данных на группы можно считать не целесообразным.
2 Множественная линейная регрессия
Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона - Pearson. 1908) состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной.
В общественных и естественных науках процедуры множественной регрессии чрезвычайно широко используются в исследованиях. В общем. множественная регрессия позволяет исследователю задать вопрос (и. вероятно. получить ответ) о том. "что является лучшим предиктором для...".
Общая вычислительная задача. которую требуется решать при анализе методом множественной регрессии. состоит в подгонке прямой линии к некоторому набору точек.В многомерном случае. когда имеется более одной независимой переменной. линия регрессии не может быть отображена в двумерном пространстве. однако она также может быть легко оценена. В общем случае. процедуры множественной регрессии будут оценивать параметры линейного уравнения вида:
Y = a + b1*X1 + b2*X2 + ... + bp*Xp
Регрессионные коэффициенты (или B-коэффициенты) представляют независимые вклады каждой независимой переменной в предсказание зависимой переменной.
Линия регрессии выражает наилучшее предсказание зависимой переменной (Y) по независимым переменным (X). Однако обычно имеется существенный разброс наблюдаемых точек относительно подогнанной прямой. Отклонение отдельной точки от линии регрессии (от предсказанного значения) называется остатком.
Чем меньше разброс значений остатков около линии регрессии по отношению к общему разбросу значений. тем. очевидно. лучше прогноз. Например. если связь между переменными X и Y отсутствует. то отношение остаточной изменчивости переменной Y к исходной дисперсии равно 1.0. Если X и Y жестко связаны. то остаточная изменчивость отсутствует. и отношение дисперсий будет равно 0.0. В большинстве случаев отношение будет лежать где-то между этими экстремальными значениями. т.е. между 0.0 и 1.0. 1.0 минус это отношение называется R-квадратом или коэффициентом детерминации. Это значение непосредственно интерпретируется следующим образом. Значение R-квадрата является индикатором степени подгонки модели к данным (значение R-квадрата близкое к 1.0 показывает. что модель объясняет почти всю изменчивость соответствующих переменных).
Обычно. степень зависимости двух или более предикторов (независимых переменных или переменных X) с зависимой переменной (Y) выражается с помощью коэффициента множественной корреляции R. По определению он равен корню квадратному из коэффициента детерминации. Это неотрицательная величина. принимающая значения между 0 и 1. Для интерпретации направления связи между переменными смотрят на знаки (плюс или минус) регрессионных коэффициентов или B-коэффициентов. Если B-коэффициент положителен. то связь этой переменной с зависимой переменной положительна; если B-коэффициент отрицателен. то и связь носит отрицательный характер. Конечно. если B-коэффициент равен 0. связь между переменными отсутствует.
Прежде всего. как это видно уже из названия множественной линейной регрессии. предполагается. что связь между переменными является линейной. На практике это предположение. в сущности. никогда не может быть подтверждено; к счастью. процедуры множественного регрессионного анализы в незначительной степени подвержены воздействию малых отклонений от этого предположения.
Основное концептуальное ограничение всех методов регрессионного анализа состоит в том. что они позволяют обнаружить только числовые зависимости. а не лежащие в их основе причинные связи.
Важность анализа остатков. Хотя большинство предположений множественной регрессии нельзя в точности проверить. исследователь может обнаружить отклонения от этих предположений. В частности. выбросы (т.е. экстремальные наблюдения) могут вызвать серьезное смещение оценок. "сдвигая" линию регрессии в определенном направлении и тем самым. вызывая смещение регрессионных коэффициентов. Часто исключение всего одного экстремального наблюдения приводит к совершенно другому результату.
Используя Matlab найдем уравнение множественной регрессии для нахождения зависимости ВАШБП и ВАШСП от других показателей а также найдем коэффициент корреляции для определения зависимости между данными выборками и критерий Фишера для определения уровня доверия к полученному уравнению.
Аппарат множественной линейной регрессии реализуется в Matlab при помощи функции regress. Анализ основывается на нахождении коэффициентов b уравнения вида:
y = b0 + b1x1 + b2x2 + b3x3 + ... + bnxn
Методом наименьших квадратов.
Входными данными для программы будут:
Матрица X по одному измерению равная длине вектора Y (ВАШБП, ВАШСП), а по другому количеству переменных, по которым должна предсказываться переменная “Y” плюс один. Ещё один столбик нам понадобиться для того, чтобы matlab мог по нему рассчитать свободный член уравнения b0, расположен он должен быть первым и заполнен единицами. Т.е. 2-й столбец матрицы X это значения Hb, 3-й столбец значения СОЭ, 4-й значения СРБ и 5-й Фибриноген.
Y – значения ВАШ (ВАШБП, ВАШСП)
Функция regress задается следующим образом:
[b.bint.r.rint.stats] = regress(y.X.0.01)
regress(y.X.0.01) – означает что мы будем искать зависимость Y от Х и с вероятностью 99% коэффициенты b будут принадлежать рассчитанным нами доверительным интервалам.
Выходные данные:
Вектор коэффициентов b.
Матрица bint. содержащая 99% доверительные интервалы для b.
Вектор r (длина которого равна длине Y). содержащий остатки. т.е. разницу между исходными значениями Y. и рассчитанными по полученному уравнению регрессии.
Матрицу rint. содержащую значения 99% доверительного интервала для r
Вектор stats. состоящий из следующих 4 характеристик:
первое значение – коэффициент множественной корреляции R2. показывающий связь исходных данных y и рассчитанных по полученному уравнению. другими словами – это коэффициент. показывающий на сколько хорошо «работает» полученное уравнение. Чем ближе это значение к единице. тем лучше.
второе значение – F-статистика (её ещё называют критерием Фишера).
третье значение – p. табличное значение критерия Фишера при данных степенях свободы. Если критерий Фишера выше этого значения. то уравнению можно верить.
четвёртое значение – оценка дисперсии ошибок
I) рассчитаем уравнение множественной линейной регрессии для ВАШБП
После выполнения расчетов для ВАШБП получили следующие переменные:
b
bint
r
rint
42.1283
1.8780
82.3786
-21.9027
-73.5518
29.7465
-0.1015
-0.3855
0.1824
-10.4547
-62.2125
41.3031
0.2908
-0.1418
0.7233
14.2154
-36.8404
65.2711
0.0326
-0.0177
0.0829
-18.2805
-68.5417
31.9806
0.7105
-3.0313
4.4524
1.2654
-50.5643
53.0951
45.7534
-5.3326
96.8394
-14.6868
-66.0309
36.6572
7.2762
-44.4701
59.0225
44.4133
-6.6808
95.5074
-5.6498
-57.3639
46.0644
10.6615
-40.5673
61.8902
41.4956
-9.2270
92.2183
5.2307
-46.4949
56.9564
14.2893
-37.3388
65.9175
-16.9757
-64.8977
30.9463
-1.7014
-52.3459
48.9432
11.3454
-40.2887
62.9794
18.1895
-33.3589
69.7380
-24.8022
-75.9894
26.3849
4.1667
-47.1548
55.4881
7.4767
-44.4040
59.3575
53.4995
2.7606
104.2384
-8.4099
-60.1502
43.3304
-8.1185
-59.1222
42.8851
34.8356
-16.4892
86.1604
7.3277
-44.1261
58.7815
-1.1282
-52.7224
50.4660
-22.7002
-73.0690
27.6685
35.3231
-15.4605
86.1067
12.1224
-39.4234
63.6682
23.2364
-28.4547
74.9275
2.0986
-49.7444
53.9416
3.3639
-48.4351
55.1629
-35.4930
-86.7043
15.7183
15.7701
-35.8987
67.4389
1.9511
-49.4156
53.3179
1.2643
-37.9653
40.4940
2.8817
-47.4120
53.1755
27.5456
-23.6290
78.7202
8.0058
-43.8027
59.8144
26.1533
-25.0770
77.3836
-11.6135
-63.2959
40.0690
14.2769
-37.5125
66.0664
-5.0043
-56.8847
46.8760
21.7829
-29.7810
73.3468
27.4824
-23.6602
78.6249
-15.3203
-66.5536
35.9129
36.8308
-14.3416
88.0032
21.9905
-29.7372
73.7183
-0.3487
-52.1580
51.4607
-14.4565
-65.3638
36.4507
2.2326
-49.4426
53.9079
-23.0332
-74.5239
28.4574
16.0495
-35.4532
67.5522
-21.3666
-72.7803
30.0472
-5.9001
-57.5397
45.7395
-13.5376
-63.5547
36.4796
7.2019
-44.2296
58.6334
-7.2965
-59.0702
44.4772
-31.3225
-82.2665
19.6215
24.7206
-26.5090
75.9502
12.0085
-29.4721
53.4890
-14.3362
-66.1232
37.4507
-19.4698
-71.0521
32.1125
-16.1754
-66.8306
34.4799
8.0639
-43.7532
59.8809
-12.2995
-64.1466
39.5476
13.9893
-37.7707
65.7493
-16.2954
-67.9216
35.3308
-12.3199
-64.0425
39.4027
-4.7723
-56.3885
46.8438
-7.6406
-59.3361
44.0548
-20.2521
-71.7464
31.2422
2.3469
-49.4690
54.1627
39.2104
-11.8405
90.2614
-16.6829
-68.1490
34.7832
-27.6404
-79.0945
23.8136
0.6820
-50.1330
51.4970
-30.4212
-81.9717
21.1294
-31.1453
-82.5884
20.2978
-24.1908
-75.6191
27.2374
18.2420
-33.1537
69.6377
7.2360
-43.3212
57.7931
-25.8891
-77.5028
25.7247
-29.9523
-81.4193
21.5148
-13.5789
-65.3925
38.2347
-23.7983
-75.2594
27.6627
-9.3176
-61.0193
42.3841
-12.2236
-64.0984
39.6512
-26.7522
-78.2955
24.7910
-19.1908
-70.7002
32.3185
-15.5540
-67.2924
36.1844
-21.6260
-72.8683
29.6163
-11.8236
-62.7620
39.1148
5.3410
-46.3573
57.0393
-26.0752
-77.4141
25.2636
-23.8405
-75.5436
27.8627
9.1271
-42.3050
60.5592
-22.0750
-73.2466
29.0966
-19.3643
-70.7356
32.0071
-5.2939
-57.0079
46.4201
-3.9155
-55.2281
47.3971
6.0662
-45.1461
57.2784
20.6750
-30.6746
72.0246
8.5343
-43.3618
60.4303
21.8225
-29.5504
73.1954
-19.4300
-70.1039
31.2439
5.9953
-45.8101
57.8006
2.0391
-49.2100
53.2883
42.8692
-7.4532
93.1915
24.0227
-27.3822
75.4275
21.6036
-29.8883
73.0954
7.9463
-42.0260
57.9186
-24.6224
-75.8610
26.6162
-18.1688
-69.9114
33.5739
-3.0542
-54.5917
48.4834
-7.0589
-58.7440
44.6261
-14.8646
-66.5830
36.8538
-3.5953
-55.2165
48.0260
-16.8888
-68.7256
34.9480
24.7304
-26.4446
75.9054
9.0011
-42.8700
60.8722
1.6549
-48.7937
52.1035
4.7382
-46.8959
56.3724
-24.8120
-76.4793
26.8554
-24.7124
-76.2026
26.7778
-10.3635
-61.9389
41.2118
-24.0183
-75.5760
27.5393
-31.1297
-82.7024
20.4430
-10.2047
-61.4757
41.0663
13.1655
-38.3588
64.6897
4.6407
-47.1058
56.3873
9.3834
-40.9519
59.7187
19.2757
-32.2076
70.7590
8.6060
-43.1614
60.3735
-0.6029
-52.3315
51.1257
15.3004
-35.5974
66.1982
11.9546
-39.5044
63.4137
22.3373
-29.2132
73.8877
7.2462
-44.4642
58.9567
-28.6600
-80.0657
22.7457
5.0618
-46.6397
56.7633
20.8124
-30.2927
71.9175
-1.2405
-52.8524
50.3713
-4.0754
-55.6256
47.4747
-13.1297
-64.9991
38.7397
-1.0570
-52.6293
50.5152
-8.9762
-60.6462
42.6938
-19.1095
-70.6665
32.4476
-7.3882
-59.1979
44.4216
-31.7918
-83.1929
19.6092
32.5654
-18.8114
83.9423
25.8476
-25.6974
77.3926
17.2462
-34.3729
68.8654
12.7771
-38.9022
64.4564
17.9586
-33.6785
69.5957
-12.4963
-64.2189
39.2263
28.2903
-23.0283
79.6090
-1.9287
-53.1104
49.2530
-20.1486
-70.8255
30.5284
12.7423
-39.0574
64.5419
-33.4366
-79.4435
12.5702
-28.3399
-79.4332
22.7535
45.9715
-4.3766
96.3197
17.6894
-33.9998
69.3786
28.8293
-22.6317
80.2902
45.0664
-5.5918
95.7246
38.6743
-12.3544
89.7029
-1.9044
-53.7565
49.9477
20.3493
-31.0914
71.7901
-17.8734
-69.5782
33.8313
-6.5057
-57.7216
44.7103
-23.8741
-75.3281
27.5800
-0.4543
-52.0199
51.1113
-9.0759
-59.6117
41.4599
6.4047
-45.2060
58.0155
-14.4330
-66.1409
37.2749
19.2787
-31.6829
70.2403
-3.4277
-54.6947
47.8392
-10.2520
-61.6535
41.1494
-28.7033
-80.0804
22.6737
-13.9223
-64.7794
36.9348
stats = 0.1569; 8.2341; 0.0000; 398.2227;
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШБП= 42.1283 – 0.1015 Hb + 0.2908 СОЭ + 0.0326 СРБ +0.7105 Фибриноген
R2=0.1569 - 15.69% от исходной изменчивости могут быть объяснены. а 84.31% остаточной изменчивости остаются необъясненными.
F=8.2341
p= 0
F>p следовательно полученному уравнению можно верить с вероятностью в 99%
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения. а затем заново рассчитаем уравнение множественной регрессии.
После вычислений получаем новые переменные и новое уравнение:
b
bint
r
rint
68.6128
42.6275
94.5981
-9.0527
-37.3058
19.2004
-0.3179
-0.4996
-0.1362
12.6863
-14.9838
40.3564
0.2660
0.0000
0.5319
4.7180
-23.6375
33.0735
0.0363
0.0073
0.0653
-7.8665
-35.8002
20.0673
0.5753
-1.9305
3.0812
8.4230
-19.8230
36.6691
-3.9845
-32.2508
24.2819
6.5985
-21.2655
34.4624
9.6122
-18.6033
37.8276
-10.2044
-35.0328
14.6240
2.7871
-24.8193
30.3934
17.2257
-10.7195
45.1709
5.4367
-22.5254
33.3988
9.2325
-19.0964
37.5614
-7.7024
-35.9560
20.5512
-1.2661
-28.9378
26.4056
14.4948
-13.4018
42.3914
7.5633
-20.5114
35.6379
-17.4951
-44.6647
9.6746
17.8317
-9.9962
45.6596
5.8425
-22.4781
34.1631
9.3237
-18.9007
37.5480
3.3445
-24.6908
31.3798
-0.8088
-21.5731
19.9554
8.6299
-18.5165
35.7762
9.9962
-18.2684
38.2609
-6.5170
-34.7503
21.7163
17.5223
-10.5451
45.5896
-2.6598
-31.0639
25.7443
-4.7289
-32.6182
23.1603
1.1007
-27.2539
29.4553
-15.4184
-42.9371
12.1002
1.9826
-26.2594
30.2246
14.9612
-12.9779
42.9002
0.3910
-27.7965
28.5784
-11.5190
-38.0908
15.0528
4.1080
-23.9282
32.1441
-2.3669
-30.6874
25.9536
5.7176
-16.0196
27.4548
-11.7715
-40.0204
16.4775
-11.6867
-39.7871
16.4137
-11.2514
-38.7594
16.2566
14.1006
-14.0387
42.2399
-7.9019
-36.2419
20.4382
18.4706
-9.5140
46.4553
-13.1757
-41.2401
14.8888
-5.9183
-34.1797
22.3430
1.5930
-26.5748
29.7608
-6.1504
-34.3885
22.0877
-11.9710
-40.0136
16.0715
4.7517
-23.5772
33.0805
-7.6354
-35.6957
20.4249
-2.5114
-30.1466
25.1238
-17.8750
-45.7099
9.9598
4.9776
-22.4033
32.3584
-9.2707
-37.5638
19.0224
-15.6411
-43.5795
12.2973
-2.0349
-30.2891
26.2193
-7.5352
-35.9057
20.8354
-12.8750
-40.8787
15.1286
-9.0399
-37.2915
19.2118
-14.1604
-41.7111
13.3903
13.3652
-14.6783
41.4087
-17.2193
-45.0403
10.6016
19.0244
-8.6055
46.6542
-11.5693
-39.3592
16.2207
-19.6532
-47.3414
8.0351
-0.6843
-28.9330
27.5644
4.5464
-23.3429
32.4356
16.7275
-10.8084
44.2634
10.5922
-17.7215
38.9060
-14.8775
-42.1330
12.3780
6.5270
-21.7825
34.8365
2.7666
-25.1568
30.6900
8.5476
-18.2907
35.3860
-13.1649
-41.3581
15.0284
-1.8218
-29.9553
26.3117
-6.6755
-34.9033
21.5523
-9.8041
-38.0180
18.4097
4.9947
-23.1450
33.1345
-12.3110
-40.5921
15.9700
12.6185
-15.6296
40.8666
0.0386
-27.2984
27.3755
6.3388
-21.8537
34.5312
-10.6292
-38.7183
17.4599
-13.4573
-41.1993
14.2847
14.4516
-13.5325
42.4357
4.6315
-23.6516
32.9145
14.3512
-12.5735
41.2759
12.0414
-16.1382
40.2210
0.5380
-27.7541
28.8300
20.0878
-7.0899
47.2654
19.1331
-8.6111
46.8774
8.7274
-19.4685
36.9234
5.4167
-22.8281
33.6615
0.3107
-27.8741
28.4954
3.1306
-24.9738
31.2350
-8.6352
-36.9898
19.7193
-2.6414
-30.7999
25.5171
-2.4350
-30.6568
25.7869
-14.3378
-42.3473
13.6717
-1.8313
-30.1660
26.5034
18.7274
-9.1685
46.6234
14.9255
-13.1336
42.9846
-11.4913
-39.6756
16.6930
-4.2104
-32.0433
23.6225
-18.6544
-45.9305
8.6218
15.6565
-12.4643
43.7773
1.5669
-26.8071
29.9410
-11.1319
-39.3470
17.0832
-7.9681
-35.8440
19.9077
3.3454
-24.8477
31.5384
-6.2493
-33.6830
21.1844
14.9947
-12.9265
42.9160
-8.0405
-36.2726
20.1915
16.5496
-10.9807
44.0799
-4.8517
-32.7475
23.0440
-9.6016
-37.5465
18.3433
-14.1529
-41.6157
13.3098
stats = 0.5231; 30.9919; 0; 118.0091;
ВАШБП= 68.6128 – 0.3179 Hb + 0.2660 СОЭ + 0.0363 СРБ +0.5753 Фибриноген
R2=0.5231 - 52.31% от исходной изменчивости могут быть объяснены. а 47.69% остаточной изменчивости остаются необъясненными.
F=30.9919
p= 0
F>p следовательно полученному уравнению можно верить.
Исключая и далее экстремальные наблюдения. возможно построить уравнение объясняющее еще больший процент изменчивости переменной Y (ВАШБП).
Построенное уравнение показывает что наилучшим предсказывающим фактором (предиктором) для ВАШБП является Фибриноген.
II) рассчитаем уравнение множественной линейной регрессии для ВАШСП
После выполнения расчетов для ВАШСП получаем:
b
bint
r
rint
34.4446
-5.3696
74.2588
-22.0047
-73.0438
29.0343
-0.0248
-0.3063
0.2567
9.4034
-41.7566
60.5635
0.4860
0.0556
0.9164
11.0867
-39.4013
61.5746
0.0269
-0.0230
0.0768
-18.9427
-68.5986
30.7132
0.6296
-3.0822
4.3415
-2.8132
-54.0347
48.4083
36.8501
-13.8945
87.5948
-28.5283
-79.0411
21.9845
-7.5443
-58.6841
43.5956
32.6494
-18.1678
83.4666
-9.1522
-60.2423
41.9378
30.8460
-19.4622
81.1541
27.5125
-22.9630
77.9879
-6.6522
-57.7655
44.4612
32.0518
-18.6502
82.7538
-22.7943
-70.0647
24.4762
-14.5034
-64.4720
35.4653
-1.6638
-52.7402
49.4126
7.6126
-43.4318
58.6569
-15.1416
-65.8714
35.5883
-20.8158
-71.3764
29.7448
12.0866
-39.1543
63.3276
40.4712
-10.1110
91.0534
13.5493
-37.5432
64.6418
-12.5814
-62.9502
37.7874
31.2113
-19.5904
82.0130
3.8039
-47.0594
54.6671
16.1928
-34.6959
67.0816
-6.6698
-56.6177
43.2782
7.4368
-43.2022
58.0757
21.2822
-29.5356
72.1001
19.1169
-32.0283
70.2620
2.5209
-48.7140
53.7558
-1.4753
-52.6685
49.7179
-8.3178
-59.3686
42.7330
20.6240
-30.3657
71.6137
11.7056
-39.0037
62.4150
2.6396
-36.0613
41.3405
12.9805
-36.6568
62.6177
31.1705
-19.3079
81.6490
11.0245
-40.1560
62.2050
27.6597
-22.9260
78.2454
-10.3585
-61.4439
40.7269
6.4906
-44.7533
57.7345
10.9088
-40.3295
62.1471
-6.3570
-57.4778
44.7639
27.4574
-23.0693
77.9842
-17.5149
-68.1171
33.0872
33.0984
-17.5583
83.7551
26.4393
-24.5970
77.4755
0.3345
-50.8698
51.5388
-6.0534
-56.4208
44.3141
3.7625
-47.3066
54.8317
-25.3221
-76.1620
25.5178
19.5298
-31.3220
70.3816
-20.8371
-71.6505
29.9762
-12.9534
-63.9315
38.0246
-20.4564
-69.7872
28.8745
-7.2787
-58.1104
43.5530
3.6446
-47.5376
54.8268
-30.3284
-80.6854
20.0286
28.0814
-22.4730
78.6359
3.9765
-37.0488
45.0017
-11.0738
-62.2851
40.1374
-14.0776
-65.1176
36.9624
-17.3640
-67.3964
32.6683
3.6203
-47.6074
54.8481
13.6091
-37.5453
64.7636
-17.4134
-68.5347
33.7079
-14.4674
-65.4316
36.4968
4.9588
-46.2466
56.1643
25.0177
-25.7733
75.8087
-25.8147
-76.5983
24.9690
-15.9546
-67.0693
35.1600
-22.5584
-73.2294
28.1126
-25.9105
-76.7866
24.9657
10.7575
-39.4114
60.9264
-37.3978
-88.1530
13.3575
-34.2591
-85.0080
16.4898
-28.4395
-79.1662
22.2873
7.1019
-43.8000
58.0038
-1.1487
-51.1280
48.8305
-25.1404
-76.1545
25.8736
-33.8536
-84.6079
16.9008
35.4639
-15.3332
86.2611
-23.3846
-74.2392
27.4701
-3.8124
-54.9315
47.3066
-18.0134
-69.2128
33.1859
-30.1234
-80.9801
20.7333
-24.4395
-75.2474
26.3685
-25.1041
-76.0837
25.8755
-0.6512
-51.4711
50.1687
-16.2161
-66.5045
34.0724
-1.5388
-52.6389
49.5613
-29.2822
-79.9380
21.3737
-20.0506
-71.2057
31.1045
7.1426
-43.6939
57.9791
-19.7381
-70.3403
30.8641
-16.6074
-67.4100
34.1953
-2.1240
-53.2381
48.9901
-19.1491
-69.7304
31.4321
7.7141
-42.8786
58.3068
12.8733
-37.9695
63.7160
-16.4096
-67.6248
34.8056
37.0681
-13.3471
87.4834
-15.4789
-65.6088
34.6509
7.4797
-43.7139
58.6732
-9.8804
-60.4900
40.7292
34.3137
-15.6535
84.2810
6.7098
-44.2910
57.7105
9.9425
-41.0808
60.9658
9.2656
-40.0972
58.6285
-32.9906
-83.4306
17.4494
0.1865
-51.0727
51.4458
-0.4577
-51.3953
50.4799
-10.3484
-61.4071
40.7103
-3.4172
-54.6044
47.7701
1.6651
-49.3512
52.6814
-10.0063
-61.3041
41.2914
15.1540
-35.5594
65.8675
3.0794
-48.2116
54.3703
5.5574
-44.2786
55.3934
11.1460
-39.8436
62.1357
-30.2489
-81.1894
20.6917
-13.1520
-64.1954
37.8915
-3.4228
-54.4306
47.5849
-17.7521
-68.8004
33.2962
-35.8769
-86.7118
14.9581
-14.4932
-65.1229
36.1365
-0.1188
-51.1060
50.8683
3.7897
-47.3559
54.9354
21.9194
-27.6652
71.5039
26.7776
-23.9676
77.5227
5.5205
-45.6555
56.6965
13.3664
-37.6893
64.4221
13.7147
-36.6026
64.0320
9.4851
-41.3890
60.3592
29.1797
-21.6240
79.9835
-15.7831
-66.8133
35.2470
-22.7078
-73.6132
28.1977
-4.3393
-55.4381
46.7594
37.4241
-12.6945
87.5427
16.4062
-34.4985
67.3108
0.1738
-50.7715
51.1190
-7.8769
-59.1793
43.4256
-13.8921
-64.7886
37.0044
-8.0860
-59.1509
42.9788
-17.1031
-68.0762
33.8699
-4.4151
-55.6334
46.8032
-30.9607
-81.7690
19.8475
32.0094
-18.7677
82.7865
31.7837
-19.0185
82.5860
5.2169
-45.8980
56.3317
-5.0515
-56.1756
46.0727
18.5197
-32.4990
69.5385
-5.7714
-56.9352
45.3925
25.2208
-25.5482
75.9898
-12.6104
-63.1297
37.9090
21.7828
-28.2603
71.8259
10.2245
-40.9908
61.4398
-9.4350
-55.3153
36.4453
-5.0919
-55.8748
45.6909
32.6112
-17.5312
82.7536
44.5121
-5.9272
94.9515
35.8486
-14.8237
86.5210
43.8482
-6.2251
93.9214
35.3981
-15.1079
85.9040
-5.3886
-56.6237
45.8465
-19.5086
-70.3569
31.3398
-28.7582
-79.6589
22.1426
-8.0440
-58.6477
42.5597
9.2664
-41.7655
60.2984
-2.1800
-53.1386
48.7786
-8.6818
-58.6147
41.2510
5.6651
-45.3400
56.6702
-18.4257
-69.4724
32.6210
12.4336
-38.0096
62.8769
-15.3049
-65.8878
35.2780
-17.3295
-68.1602
33.5013
-2.4444
-53.5238
48.6351
-13.7255
-64.1018
36.6508
stats = 0.2171 12.1355 0.0000 388.8866
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШСП= 34.4446 – 0.0248 Hb + 0.4860 СОЭ + 0.0269 СРБ +0.6 296Фибриноген
R2=0.2171 - 21.71% от исходной изменчивости могут быть объяснены
F=12.1355
p= 0
F>p следовательно полученному уравнению можно верить.
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения. а затем заново рассчитаем уравнение множественной регрессии.
Новое уравнение будет выглядеть следующим образом:
ВАШСП= 32.6943 – 0.0638 Hb + 0.4418 СОЭ + 0.0269 СРБ +1.9637 Фибриноген
stats =0.5550; 34.9170; 0; 111.2369;
R2=0.5550 - 55.50% от исходной изменчивости могут быть объяснены
F=34.9170
p= 0
F>p следовательно полученному уравнению можно верить.
Вывод: исходя из полученного уравнения, можно сделать вывод о том, что наилучшим предсказывающим фактором для ВАШСП является фибриноген.
Зависимость ВАШБП и ВАШСП от показателей активности в динамике
Разобьем наши данные на три группы. В первую группу войдут данные полученные до лечения. во вторую данные после 2 месяцев лечения а в третью после трех месяцев.
Так как ранее мы уже проводили исследование на проверку распределения выборок то мы можем воспользоваться параметрическим методом дисперсионного анализа для проверки различий средних. Проверка необходима для подтверждения целесообразности разделения данных, если это подтвердится, то затем мы рассчитаем для каждой группы уравнение зависимости ВАШСП и ВАШБП от показателей активности заболевания.
3 Дисперсионный анализ
Таблица 2.1.1. Зависимость Hb от стадии лечения
1 группа
2 группа
3 группа
124
125
134
124
115
104
110
118
130
93
117
136
133
114
150
129
123
136
149
150
105
122
125
146
145
103
146
124
142
138
99
150
158
125
140
154
137
94
141
156
129
134
148
156
150
138
141
150
144
148
114
133
141
109
145
135
157
121
150
161
126
150
133
128
127
166
120
158
168
150
131
136
123
162
142
150
121
118
160
144
126
139
160
140
152
140
101
146
110
123
142
135
117
137
106
151
148
126
142
130
154
144
152
140
120
126
110
107
118
116
114
140
136
124
166
122
120
128
150
115
165
112
143
124
132
137
130
130
126
160
166
150
168
128
126
114
142
156
170
119
128
163
135
120
120
106
130
156
114
137
142
121
140
121
136
125
138
150
154
127
153
120
171
128
124
130
127
130
138
122
160
104
121
131
127
109
158
132
134
164
После вычислений получаем:
p =0.7913
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.1.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
136,7
2
68,326
Остаточная
51587,5
177
291,455
Полная
51724,2
179
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень гемоглобина в крови не зависит от стадии лечения.
Таблица 2.2.1. Зависимость СОЭ от стадии лечения
1 группа
2 группа
3 группа
18
14
5
19
4
10
42
12
15
66
17
3
25
14
3
10
5
38
13
2
49
28
40
5
3
30
3
26
6
19
28
3
2
38
26
3
28
69
10
1
25
5
52
3
3
48
35
5
26
6
16
14
3
5
12
5
4
48
1
4
19
5
10
28
5
1
25
7
4
6
6
15
11
3
2
26
10
10
2
2
10
51
2
10
24
12
34
13
37
38
6
18
25
10
58
2
2
10
10
30
4
17
2
10
15
3
23
8
46
12
5
56
5
10
3
12
35
11
12
39
4
10
4
30
24
24
11
40
7
2
1
2
7
9
20
34
4
24
1
35
16
1
36
22
34
50
28
14
64
30
9
32
10
21
3
7
22
26
12
6
1
18
1
2
10
26
6
4
12
25
4
40
52
18
62
40
7
5
3
8
После вычислений получаем:
p = 0.0219
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.2.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
136,7
2
68,326
Остаточная
51587,5
177
291,455
Полная
51724,2
179
-----
p
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости СОЭ зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие. Для проверки такой параметрической гипотезы используется процедура множественного сравнения. При проверке простой параметрической гипотезы (нулевой гипотезы) о равенстве средних одной группы выборок по отношению к другой по статистике t необходимо задать уровень значимости , определяющий критическое значение статистики. Примем равным 0,05. Это означает, что в 5% случаев будет неверно отвергнута нулевая гипотеза.
При увеличении групп выборок, увеличивается число проверяемых гипотез.
При использовании простой параметрической гипотезы по статистике t, уровень значимости будет применяться к каждой гипотезе отдельно, что повлечет к росту вероятности неверно отвергнуть нулевую гипотезу пропорционально количеству выполненных проверок. Т.е., неверно определить значимое отличие выборочных средних. Процедура множественного сравнения обеспечивает заданный уровень значимости для каждой проверки.
Выходной параметр с представляет результаты множественного сравнения в виде матрицы из 5 столбцов. Срока матрицы с соответствуют результатам проверки одной параметрической гипотезы. Таким образом, каждая строка с соответствует одной паре выборок. Первые два значения в строке с показывают номера сравниваемых выборок, пятый - величину разности средних арифметических сравниваемых выборок, четвертый и третий столбцы - 95% доверительный интервал полученной разности средних арифметических.
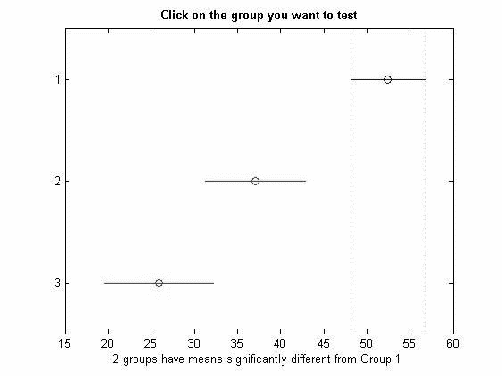
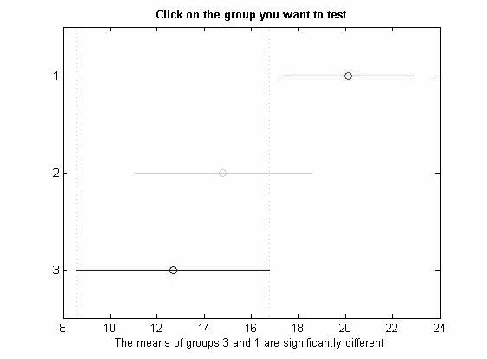
Таблица 2.2.3 Различия между средними для СОЭ
№ группы
№ группы
Нижняя граница доверительного интервала
Разница средних арифметических
Верхняя граница доверительного интервала
1 группа
2 группа
-1.2331
5.3127
11.8585
1 группа
3 группа
0.5745
7.4420
14.3096
2 группа
3 группа
-5.7354
2.1293
9.9941
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 3 группой, величина их разности равна 7.4420, 95% доверительный интервал полученной разности средних арифметических составил [0,5745, 14.3096]. Различия считаются значимыми, если в доверительный интервал не попало нулевое значение. Т.е. средние арифметические выборок статистически значимо отличаются друг от друга, для .
Отобразим графически значения средних арифметических и их доверительных интервалов. Два выборочных средних значимо отличаются, если их доверительные интервалы не пересекаются на графике. При наложении границ доверительных интервалов двух средних арифметических, различие между ними можно считать статистически незначимым.
Таблица 2.3.1. Зависимость СРБ от стадии лечения
1 группа
2 группа
3 группа
0
0
0
6
0
0
96
0
0
192
0
0
0
6
0
0
0
96
0
0
48
0
192
0
0
48
0
0
0
48
48
0
0
0
192
0
12
768
6
0
6
0
384
0
0
192
96
0
12
24
0
48
6
0
0
0
0
96
0
0
0
0
0
48
0
0
0
0
0
12
0
0
6
0
0
6
0
0
0
0
0
96
0
0
48
0
12
6
0
96
0
0
0
0
48
0
0
0
0
0
0
48
0
0
0
0
12
0
768
0
0
96
0
0
0
0
48
0
0
48
0
0
0
96
0
96
12
48
0
0
0
0
6
0
6
6
0
48
0
6
6
0
12
0
0
192
0
6
48
6
0
0
0
0
0
0
12
12
6
0
0
48
0
0
0
0
0
0
96
0
0
0
48
0
384
48
0
0
0
0
После вычислений:
p = 0.4019
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.3.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
16791,5
2
8395,73
Остаточная
1621687,7
177
9162,08
Полная
1638479,2
179
-----
p>pкр
Вывод:
Следовательно мы принимаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости уровень СРБ в крови не зависит от стадии лечения.
Таблица 2.4.1. Зависимость фибриногена от стадии лечения
1 группа
2 группа
3 группа
3,00
4,00
3,75
4,50
4,00
4,00
3,50
3,00
3,00
7,25
4,00
2,75
4,00
3,00
2,00
3,25
3,20
6,00
5,50
2,00
3,50
4,00
8,75
3,00
3,25
4,00
2,50
5,00
4,00
4,75
3,60
5,00
3,00
4,25
5,00
2,75
4,25
7,50
3,25
3,00
4,00
2,50
10,20
3,25
2,00
4,75
2,90
3,10
4,50
3,25
2,00
5,00
2,90
3,25
5,50
3,00
3,25
5,50
2,00
3,00
3,75
3,00
3,25
3,75
2,00
3,25
4,50
3,00
4,00
5,75
2,93
3,00
3,00
4,25
2,00
4,25
3,25
3,25
3,75
2,50
2,50
5,25
3,00
3,25
6,25
3,50
4,30
2,25
5,00
4,25
3,25
3,30
4,00
2,50
5,00
2,25
2,75
4,25
2,10
4,00
2,00
4,75
2,75
3,25
3,50
4,00
4,25
3,00
4,50
3,50
2,00
6,75
3,00
1,75
3,25
2,00
4,25
3,75
3,50
3,00
3,25
4,00
4,00
3,50
4,25
3,00
3,50
2,75
2,60
3,00
2,75
2,75
4,25
2,00
3,75
5,25
2,00
5,75
2,50
5,50
3,50
3,25
7,25
3,75
3,00
7,00
5,50
4,00
7,50
3,50
4,00
5,50
6,75
2,50
3,10
3,00
6,75
4,50
3,50
2,50
2,50
4,50
3,00
2,15
2,80
3,75
2,50
3,00
3,25
3,50
3,75
5,25
5,10
4,50
12,20
5,75
5,50
3,00
2,50
3,00
p = 0.0003
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.4.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
34,806
2
17,4029
Остаточная
365,662
177
2,0659
Полная
400,467
179
-----
p
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости фибриноген зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
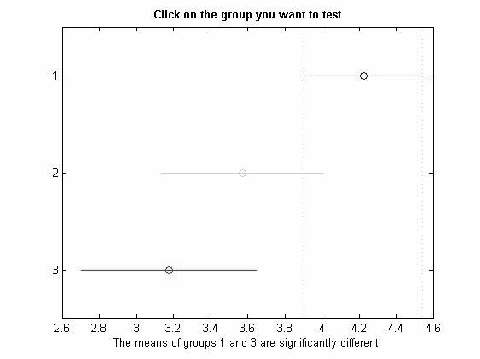
Таблица 2.4.3 Различия между средними для фибриногена
№ группы
№ группы
Нижняя граница доверительно интервала
Разница средних арифметических
Верхняя граница доверительного интервала
1 группа
2 группа
-0.1003
0.6532
1.4067
1 группа
3 группа
0.2579
1.0484
1.8389
2 группа
3 группа
-0.5101
0.3952
1.3005
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 3 группой, величина их разности равна 1.0484, 95% доверительный интервал полученной разности средних арифметических составил [0,2579, 1.8389]. Т.е. средние арифметические выборок статистически значимо отличаются друг от друга, для .
Отобразим графически значения средних арифметических и их доверительных интервалов.
Таблица 2.5.1. Зависимость ВАШБП от стадии лечения
1 группа
2 группа
3 группа
15
36
5
28
20
38
63
38
5
45
15
0
40
53
5
80
12
65
20
23
57
48
40
5
75
52
0
35
25
25
55
0
5
85
70
20
45
95
21
43
25
5
45
10
10
50
27
15
50
40
15
56
45
23
10
15
35
55
17
3
45
25
10
95
25
37
32
10
7
25
35
10
70
12
5
45
28
25
28
15
10
27
25
2
75
17
35
45
70
60
55
45
45
35
55
20
33
40
13
5
25
30
45
20
5
35
40
55
73
75
30
55
30
25
56
55
16
43
15
30
55
30
20
20
53
40
30
35
55
35
55
15
15
70
60
25
25
35
33
65
45
50
25
45
44
100
65
55
64
15
15
40
45
57
40
33
55
50
55
40
0
45
48
30
67
65
50
45
55
27
58
45
30
50
35
20
78
50
60
75
После вычислений получаем:
p = 4.8659e-011
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.5.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
19350,2
2
9675,1
Остаточная
62873,6
177
355,22
Полная
82223,8
179
-----
p
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости ВАШБП зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
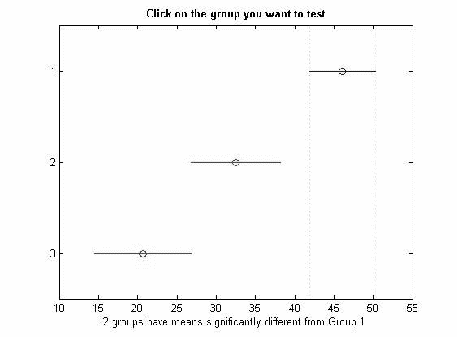
Таблица 2.5.3 Различия между средними для ВАШБП
№ группы
№ группы
Нижняя граница доверительно интервала
Разница средних арифметических
Верхняя граница доверительного интервала
1 группа
2 группа
3,7045
13,5851
23,4657
1 группа
3 группа
15,0439
25,4101
35,7763
2 группа
3 группа
-0.0464
11,8250
23,6964
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 2 группой и 1 и 3 группой.
Отобразим графически значения средних арифметических и их доверительных интервалов.
Таблица 2.6.1. Зависимость ВАШСП от стадии лечения
1 группа
2 группа
3 группа
20
41
10
53
30
50
68
43
3
55
17
0
43
60
5
75
15
63
12
20
58
40
41
10
67
43
0
38
40
80
80
5
10
80
80
30
41
95
20
65
35
5
50
20
9
48
35
10
45
40
40
50
48
20
25
18
33
40
18
5
55
40
18
89
60
40
60
10
15
25
20
10
70
12
20
50
28
35
50
30
20
55
35
2
55
29
37
60
68
55
55
45
50
40
70
25
32
50
20
40
34
39
54
30
10
47
32
50
80
75
20
78
30
20
65
19
50
50
10
40
62
31
25
60
52
45
50
45
30
39
60
15
19
70
70
35
32
28
40
65
25
70
38
52
40
100
55
50
78
15
38
50
62
70
40
50
60
56
68
20
10
40
70
50
70
78
41
30
60
40
60
42
83
53
70
51
70
80
70
80
После вычислений получаем:
p =1.0573e-011
Запишем выходные данные в таблицу дисперсионного анализа
Таблица №2.6.2. Дисперсионный анализ по одному признаку.
Компонента дисперсии
Сумма квадратов
Степень свободы
Средний квадрат
Между выборками
21595,1
2
10797,6
Остаточная
65337,4
177
369,1
Полная
86932,6
179
-----
p
Вывод:
Следовательно мы отвергаем нулевую гипотезу, т.е. можно предположить что при 5% уровне значимости ВАШСП зависит от стадии лечения. Используя функцию multcompare, целесообразно определить для какой пары выборок средние арифметические значения имеют статистически значимое различие.
Таблица 2.6.3 Различия между средними для ВАШСП
№ группы
№ группы
Нижняя граница доверительно интервала
Разница средних арифметических
Верхняя граница доверительного интервала
1 группа
2 группа
5,2663
15,3386
25,4109
1 группа
3 группа
15,9332
26,5005
37,0679
2 группа
3 группа
-0.9398
11,1620
23,2637
Полученные значения показывают, что значимая разница средних арифметических наблюдается между 1 и 2 группой и 1 и 3 группой.
Отобразим графически значения средних арифметических и их доверительных интервалов.
4 Линейная регрессия
1. Построим уравнение зависимости ВАШБП и ВАШСП для первой группы
После выполнения расчетов для ВАШБП получаем:
b
bint
r
rint
55.5897
-1.0234
112.2027
-32.5449
-81.3671
16.2774
-0.0352
-0.4366
0.3663
-16.7412
-66.1905
32.7082
0.1469
-0.4263
0.7201
9.0742
-39.3668
57.5152
0.0356
-0.0260
0.0972
-8.5563
-55.9419
38.8293
-2.1095
-6.7707
2.5517
-6.1470
-55.9481
43.6541
34.3332
-14.4218
83.0883
-20.6578
-69.6085
28.2929
1.0256
-48.6646
50.7159
30.9239
-18.0042
79.8520
-9.5008
-59.1208
40.1192
4.6638
-43.7703
53.0980
37.1898
-10.8186
85.1982
-1.3469
-51.0447
48.3509
-0.9230
-50.3921
48.5461
-5.1806
-49.4128
39.0516
-4.6042
-52.2626
43.0542
4.7203
-44.8871
54.3278
11.8687
-37.5070
61.2444
-30.6516
-79.1407
17.8375
4.7988
-44.2927
53.8902
-1.0393
-50.8820
48.8034
45.9999
-2.0349
94.0347
-13.5494
-63.0684
35.9696
-14.4945
-62.8987
33.9097
23.2344
-25.8160
72.2847
-0.3824
-49.5880
48.8231
-14.3471
-63.5227
34.8285
-23.5363
-70.7562
23.6836
32.7050
-15.5714
80.9813
-2.8328
-52.0938
46.4282
10.3778
-39.3362
60.0918
-11.9676
-61.5539
37.6187
-11.8785
-61.3934
37.6363
-41.9868
-90.1676
6.1939
0.2621
-49.2959
49.8201
-8.1621
-56.7824
40.4582
-3.0527
-28.9716
22.8662
6.9288
-40.5712
54.4287
12.6622
-36.2299
61.5544
-1.7940
-51.4348
47.8467
11.4802
-37.4851
60.4455
-22.7112
-71.8517
26.4293
7.4921
-42.3668
57.3509
-15.6784
-65.2347
33.8778
8.2972
-41.0592
57.6536
10.9012
-37.9236
59.7261
-26.9591
-75.2568
21.3387
21.8081
-27.1771
70.7933
13.6002
-36.1128
63.3132
-20.7137
-69.7056
28.2783
-21.9653
-71.0527
27.1220
-8.2091
-57.2974
40.8792
-11.4855
-59.8857
36.9147
19.8426
-29.2750
68.9603
-1.2694
-51.1186
48.5798
6.8505
-42.3175
56.0185
-16.2637
-64.7218
32.1944
-1.6909
-51.3675
47.9858
-6.0354
-54.7918
42.7211
48.7233
2.2018
95.2447
21.4711
-27.8084
70.7507
11.0636
-38.3336
60.4607
17.1311
-30.0069
64.2690
-33.0091
-81.2869
15.2687
-28.4807
-77.6532
20.6918
-4.4328
-53.8928
45.0273
7.1032
-40.3586
54.5650
7.8543
-41.4167
57.1253
-4.7090
-54.2491
44.8311
-12.8942
-62.1290
36.3406
14.8432
-33.7018
63.3881
4.9313
-44.3565
54.2190
10.2322
-39.2524
59.7168
-6.7317
-56.0897
42.6263
-45.0832
-92.8981
2.7317
-1.2306
-50.6325
48.1713
4.6044
-44.0055
53.2143
-16.8474
-65.7849
32.0901
20.2082
-28.9442
69.3606
18.0733
-31.4132
67.5598
3.2683
-46.1174
52.6539
-0.2778
-49.6871
49.1316
5.9373
-43.6017
55.4764
-20.5885
-69.9104
28.7334
15.3592
-33.8331
64.5514
-1.7328
-50.4724
47.0067
-19.9232
-67.8864
28.0400
5.8655
-43.9565
55.6874
-13.1686
-54.8756
28.5383
-27.2116
-75.7461
21.3230
38.5398
-9.0647
86.1444
4.6457
-44.8956
54.1870
13.9550
-35.3909
63.3008
30.3302
-17.8422
78.5026
stats =0.0513 1.2021 0.3156 360.6221
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШБП= 55.5897 – 0.0352 Hb + 0.1469 СОЭ + 0.0356 СРБ -2.1095Фибриноген
R2=0.0513 - 5.13% от исходной изменчивости могут быть объяснены
F=1.2021
p= 0.3156
F>p следовательно полученному уравнению можно верить.
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения, а затем заново рассчитаем уравнение множественной регрессии.
Новое уравнение будет выглядеть следующим образом:
ВАШБП= 39,5747 +0,1252 Hb + 0.3508СОЭ + 0.0253 СРБ -4,0355 Фибриноген
stats =0.2812 5.5758 0.0007 78.6334
R2=0.2812 - 28,12% от исходной изменчивости могут быть объяснены
F=5,5758
p= 0
F>p следовательно полученному уравнению можно верить..
После выполнения расчетов для ВАШСП получаем:
b
bint
r
rint
50.8776
-3.1564
104.9115
-32.7325
-79.2404
13.7754
0.0166
-0.3665
0.3998
2.5397
-44.8640
49.9434
0.2963
-0.2508
0.8434
6.0810
-40.1855
52.3475
0.0337
-0.0252
0.0925
-10.0531
-55.2500
35.1438
-1.8469
-6.2958
2.6019
-10.1094
-57.5855
37.3666
25.0166
-21.8947
71.9280
-35.0493
-81.0569
10.9584
-13.8155
-61.0841
33.4531
18.8248
-28.3079
65.9575
-13.4091
-60.6874
33.8691
24.2126
-21.5301
69.9554
23.6332
-22.7868
70.0532
-13.0071
-60.3015
34.2874
16.7728
-30.2081
63.7536
-12.8332
-54.9193
29.2530
-17.0851
-62.3357
28.1656
-8.0691
-55.3793
39.2411
0.3814
-46.8518
47.6146
-21.6864
-68.2933
24.9205
-20.1860
-66.7151
26.3432
3.3231
-44.2405
50.8868
33.0074
-13.5531
79.5680
8.0302
-39.3183
55.3788
-19.9338
-65.9570
26.0893
19.1564
-27.7641
66.0770
-3.4287
-50.3828
43.5255
2.7951
-44.2907
49.8809
-6.8360
-52.3028
38.6309
4.4110
-42.4748
51.2967
6.7961
-40.1882
53.7803
5.9857
-41.5151
53.4865
-11.5016
-58.8274
35.8241
-16.8523
-63.9817
30.2772
-14.5411
-61.7055
32.6233
5.0812
-42.1976
52.3600
0.5260
-45.9305
46.9824
-4.0088
-28.7348
20.7172
17.4362
-27.6732
62.5457
16.4756
-30.0832
63.0344
0.6604
-46.7209
48.0417
13.1959
-33.4931
59.8849
-22.0531
-68.9410
24.8349
-0.3347
-47.9643
47.2949
-0.2385
-47.7231
47.2461
-20.2450
-67.0619
26.5718
11.1447
-35.4423
57.7317
-29.0980
-75.0374
16.8415
18.0209
-28.8239
64.8657
17.8249
-29.4994
65.1491
-18.3536
-65.1590
28.4519
-18.7303
-65.6559
28.1952
-23.5790
-70.0136
22.8555
-9.3835
-55.6061
36.8390
11.7287
-35.3366
58.7939
-26.4849
-73.4803
20.5106
22.1181
-24.4339
68.6701
-12.8035
-59.1195
33.5125
-0.4660
-47.8815
46.9495
-17.4071
-63.7135
28.8994
39.0101
-5.9565
83.9767
3.8219
-43.5506
51.1945
-0.4344
-47.6739
46.8052
18.4989
-26.4261
63.4238
-40.7830
-86.2847
4.7188
-10.5180
-57.9744
36.9384
-2.2137
-49.4313
45.0039
18.2980
-26.7498
63.3459
15.5050
-31.3669
62.3769
-8.3026
-55.5452
38.9400
0.5104
-46.6079
47.6286
12.3716
-34.0022
58.7454
2.8311
-44.2230
49.8853
17.2681
-29.7928
64.3289
-30.1500
-76.5286
16.2285
-39.1008
-85.0149
6.8132
-11.5112
-58.5528
35.5305
21.5233
-24.4938
67.5404
0.3722
-46.5532
47.2975
19.2687
-27.6451
66.1824
24.1824
-22.8096
71.1744
-9.1500
-56.2240
37.9239
-18.6838
-65.5500
28.1823
6.0431
-41.2354
53.3216
-13.8500
-61.0871
33.3872
12.2025
-34.8040
59.2090
-12.7632
-59.1466
33.6201
22.5056
-23.1477
68.1590
2.9215
-44.6495
50.4926
8.2468
-31.6490
48.1426
-4.5385
-51.4144
42.3374
24.5790
-21.5012
70.6591
30.9866
-15.5081
77.4813
20.6225
-26.2676
67.5126
29.5655
-16.3814
75.5124
stats =0.0890 2.1745 0.0783 328.5125
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШСП= 50.8776 + 0.0166 Hb + 0.2963 СОЭ + 0.0337 СРБ -1.8469Фибриноген
R2=0.0890 - 8.9% от исходной изменчивости могут быть объяснены
F=2.1745
p= 0.0783
F>p следовательно полученному уравнению можно верить.
Далее произведем анализ остатков и исключим из выборки экстремальные наблюдения, а затем заново рассчитаем уравнение множественной регрессии.
Новое уравнение будет выглядеть следующим образом:
ВАШСП= 39.8065 +0,0884 Hb + 0.0029СОЭ + 0.0389 СРБ -0.4223 Фибриноген
stats = 0.2067 3.3879 0.0155 86.9531
R2=0.2067 - 20,67% от исходной изменчивости могут быть объяснены
F=3.3879
p= 0.0155
F>p следовательно полученному уравнению можно верить.
Рассчитаем уравнение зависимости ВАШБП и ВАШСП для 2 группы
После выполнения расчетов для ВАШБП получаем:
b
bint
r
rint
90.4842
24.1462
156.8221
2.8245
-34.9728
40.6217
-0.4358
-0.8641
-0.0074
-14.6052
-49.9660
20.7557
0.2928
-0.3478
0.9334
0.6256
-36.7237
37.9750
0.0538
-0.0164
0.1239
-22.5401
-58.7748
13.6946
-1.7341
-7.8643
4.3962
12.9742
-23.6786
49.6270
-20.7990
-56.9699
15.3718
0.7644
-36.4334
37.9622
-2.8781
-30.9361
25.1800
1.9709
-34.6095
38.5513
1.5751
-36.0531
39.2034
-17.3262
-52.1622
17.5098
31.2551
-3.0712
65.5815
-3.0250
-15.1183
9.0683
-9.9760
-47.2306
27.2785
-7.7462
-44.9435
29.4512
-12.4228
-46.8670
22.0214
16.5984
-20.5358
53.7326
19.7876
-17.0973
56.6725
-12.9166
-50.4226
24.5895
-4.9428
-42.0645
32.1789
3.6200
-34.1044
41.3445
-8.1368
-44.7904
28.5168
-8.4794
-45.4469
28.4882
4.9262
-32.8340
42.6863
-1.3975
-37.3390
34.5441
-7.0479
-44.4758
30.3800
-8.9832
-46.4682
28.5018
8.8562
-28.0135
45.7259
-9.9203
-47.7456
27.9049
25.2873
-8.4246
58.9992
13.7971
-23.6589
51.2531
-0.1864
-31.3211
30.9483
8.8650
-28.3947
46.1247
3.9219
-33.0458
40.8895
-6.7682
-44.7624
31.2260
-2.5593
-39.5951
34.4765
37.6211
3.9880
71.2542
2.5192
-35.3996
40.4380
17.6346
-18.2831
53.5524
-7.5626
-44.9665
29.8413
-7.6693
-44.0037
28.6650
-24.3264
-60.2566
11.6038
2.2284
-34.9823
39.4392
-8.3589
-42.0641
25.3464
18.8562
-17.3214
55.0339
-5.9350
-43.5076
31.6375
stats =0.5157 10.9162 0.0000 199.2977
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШБП= 90,4842 -0,4358 Hb + 0.2928 СОЭ + 0.0538 СРБ -1.7341Фибриноген
R2=0.5157 - 51,57% от исходной изменчивости могут быть объяснены
F=10,9162
p= 0
F>p следовательно полученному уравнению можно верить.
Так как больше половины от исходной изменчивости переменной ВАШБП могут быть объяснены данным уравнением то проводить исключение выскакивающих вариант мы не будем.
После выполнения расчетов для ВАШСП получаем:
b
bint
r
rint
74.6060
3.7587
145.4533
4.5575
-35.7827
44.8976
-0.2903
-0.7478
0.1671
-4.5586
-42.8568
33.7395
0.4787
-0.2054
1.1629
3.3394
-36.5243
43.2031
0.0482
-0.0267
0.1232
-23.2016
-61.9962
15.5931
-2.1431
-8.6900
4.4039
17.9311
-20.9102
56.7724
-19.4290
-58.3313
19.4733
-7.7251
-47.3157
31.8655
-6.9728
-36.8187
22.8730
-9.8057
-48.6580
29.0465
12.3233
-27.5231
52.1697
-16.7746
-54.1278
20.5786
35.0482
-1.3264
71.4227
-6.3240
-19.0289
6.3809
-5.8368
-45.8054
34.1318
-3.7829
-43.6328
36.0670
-13.8393
-50.5864
22.9079
11.3002
-28.7849
51.3854
18.8223
-20.7830
58.4276
-13.3735
-53.4550
26.7081
-9.2464
-48.7586
30.2659
12.9817
-26.9578
52.9213
24.1607
-13.7819
62.1032
-15.6529
-54.7550
23.4491
-13.1636
-53.1599
26.8327
-7.8977
-46.1393
30.3438
-9.2963
-49.2004
30.6078
1.6043
-38.6321
41.8407
12.3215
-26.9097
51.5527
-3.2014
-43.8275
37.4247
18.3343
-18.6518
55.3204
8.0458
-32.3022
48.3939
6.8037
-26.3203
39.9276
16.2985
-23.0884
55.6855
6.4788
-32.9453
45.9029
-1.7797
-42.4667
38.9074
-13.1496
-52.3195
26.0204
35.8303
-0.9187
72.5792
-1.0831
-41.5932
39.4269
-21.6423
-59.7303
16.4457
-19.2979
-58.5368
19.9410
-7.3021
-46.1387
31.5344
9.9044
-29.8156
49.6244
0.4798
-39.2728
40.2324
-7.4326
-43.4909
28.6257
16.3215
-22.6425
55.2854
-11.1178
-51.0543
28.8187
stats = 0.4741 9.2403 0.0000 227.3133
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШСП= 74,6060 -0,2903 Hb + 0.4787 СОЭ + 0.0482 СРБ -2,1431Фибриноген
R2=0.4741 - 47,41% от исходной изменчивости могут быть объяснены
F=9,2403
p= 0
F>p следовательно полученному уравнению можно верить.
Построим уравнение зависимости ВАШБП и ВАШСП в 3 группе
После выполнения расчетов для ВАШБП получаем:
b
bint
r
rint
51.9250
-16.2666
120.1166
-14.2935
-48.4355
19.8485
-0.3334
-0.7714
0.1046
8.1518
-23.4159
39.7194
-0.0539
-1.0565
0.9488
-12.6251
-47.5751
22.3250
0.3274
-0.1187
0.7736
-15.4497
-50.1677
19.2684
3.2847
-5.2879
11.8572
-3.3181
-37.9505
31.3143
9.3268
-19.0731
37.7267
15.5114
-13.2881
44.3109
-7.8288
-43.3208
27.6632
-11.2942
-46.3668
23.7785
-11.2071
-44.5562
22.1420
-3.9892
-39.0154
31.0369
10.5521
-24.4140
45.5182
3.9876
-31.7774
39.7526
-10.1876
-45.3800
25.0047
1.6819
-32.9763
36.3400
3.1765
-32.2848
38.6378
-4.6214
-38.7327
29.4899
-2.9869
-35.5847
29.6109
24.9639
-8.0240
57.9519
-4.8812
-39.5228
29.7604
-7.7152
-43.2511
27.8206
29.8032
-1.5126
61.1190
-1.8318
-34.4443
30.7806
-5.6245
-40.7179
29.4690
-6.0394
-40.6636
28.5847
2.2833
-32.7475
37.3140
-7.5858
-42.9437
27.7722
-13.3812
-48.4307
21.6683
0.5296
-30.6683
31.7274
5.7404
-22.5060
33.9868
20.2943
-10.7267
51.3154
11.1403
-23.4900
45.7705
2.0630
-32.7541
36.8801
-4.3143
-37.7294
29.1009
-17.6017
-51.7051
16.5017
29.3290
-1.1442
59.8022
9.7861
-22.9731
42.5453
9.2109
-24.7332
43.1550
-23.7047
-56.2236
8.8141
-7.0506
-39.0017
24.9005
stats = 0.5009 8.7816 0.0001 173.5544
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШБП= 51,9250 -0,3334 Hb +0,3274 СОЭ - 0.0534 СРБ +3,2847Фибриноген
R2=0,5009 - 50,09% от исходной изменчивости могут быть объяснены
F=8,7816
p= 0.0001
F>p следовательно полученному уравнению можно верить.
После выполнения расчетов для ВАШСП получаем:
b
bint
r
rint
44.7235
-27.8214
117.2684
-15.6190
-51.9023
20.6643
-0.3118
-0.7778
0.1541
13.4645
-19.7720
46.7010
0.0107
-1.0559
1.0774
-19.4484
-56.0444
17.1477
0.3283
-0.1464
0.8029
-18.9404
-55.6121
17.7314
6.0335
-3.0863
15.1533
-5.0498
-41.8544
31.7548
-7.4380
-37.8063
22.9302
8.6181
-22.7173
39.9534
-7.3520
-45.1540
30.4499
-14.3138
-51.4481
22.8204
33.6879
1.4068
65.9691
-3.5780
-40.8555
33.6994
16.6724
-20.0775
53.4222
-2.4427
-40.5253
35.6399
-13.0771
-50.3597
24.2055
-1.0498
-37.9267
35.8271
-6.7081
-44.3360
30.9198
18.5853
-16.7246
53.8952
-10.3977
-44.7668
23.9713
17.5803
-18.7245
53.8852
-7.6640
-44.4229
29.0949
-4.9677
-42.8951
32.9598
27.4189
-6.7161
61.5538
-1.5148
-36.2139
33.1844
-10.5774
-47.6882
26.5333
7.4664
-29.3253
44.2580
7.3551
-29.7707
44.4808
-0.6253
-38.4278
37.1772
-18.7849
-55.6298
18.0599
-6.4776
-39.5299
26.5747
-8.9331
-38.8279
20.9618
17.3573
-16.1847
50.8992
13.7644
-22.9312
50.4600
6.7772
-30.1412
43.6957
-5.4197
-40.9425
30.1031
-18.5833
-54.8797
17.7131
20.4549
-13.7811
54.6908
-1.2967
-36.4797
33.8862
3.2762
-33.0916
39.6440
0.9204
-35.6226
37.4633
-3.1398
-37.2792
30.9997
stats = 0.5571 11.0045 0.0000 196.4207
Следовательно наше уравнение будет выглядеть следующим образом:
ВАШСП= 44,7235 – 0,3118 Hb + 0.3283 СОЭ + 0.0107 СРБ +6,0335Фибриноген
R2=0.5571 - 55,71% от исходной изменчивости могут быть объяснены
F=11,0045
p= 0
F>p следовательно полученному уравнению можно верить.
Заключение
В данной дипломной работе был проведен математический анализ заболевания реактивный артрит.
Был проведен анализ связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами), а именно показателями активности заболевания и зависимой переменной ВАШ (ВАШБП, ВАШСП).
Полученные уравнения показали, что лучшими предсказывающими факторами (предикторами) для ВАШБП являются уровень фибриногена и гемоглобина в крови, причем связь с гемоглобином носит отрицательный характер, а с фибриногеном положительный. Для ВАШСП лучшими предикторами будут уровень фибриногена в крови и СОЭ, для обоих факторов связь носит положительный характер.
Так же был проведен регрессионный анализ в динамике, в результате которого было установлено что в первой группе (начало лечения) лучшими предсказывающими факторами для ВАШСП и ВАШБП являются уровень фибриногена в крови и СОЭ, причем связь с СОЭ носит положительный характер а связь с фибриногеном отрицательный. Во второй (2 месяца лечения ) группе для ВАШБП – фибриноген и гемоглобин, для обоих факторов связь имеет отрицательный характер. Для ВАШСП – фибриноген и СОЭ, связь с фибриногеном носит отрицательный характер. В третьей (3 месяца лечения) группе для ВАШСП и ВАШБП – фибриноген, гемоглобин, СОЭ, связь носит отрицательный характер только для гемоглобина. Эти данные приведены ниже в таблице.
1 группа
(Начало лечения)
2 группа
(2 месяца)
3 группа
(3 месяца)
Общее уравнение
ВАШБП
1-й предиктор
Фибриноген
Фибриноген
Фибриноген
Фибриноген
2-й предиктор
СОЭ
Гемоглобин
Hb/СОЭ
Гемоглобин
Характер связи
с первым предиктором
отрицательный
отрицательный
положительный
положительный
Характер связи
со вторым предиктором
положительный
отрицательный
Отрицательный/
положительный
отрицательный
ВАШСП
1-й предиктор
Фибриноген
Фибриноген
Фибриноген
Фибриноген
2-й предиктор
Гемоглобин
СОЭ
Hb/СОЭ
СОЭ
Характер связи
с первым предиктором
отрицательный
отрицательный
отрицательный
положительный
Характер связи
со вторым предиктором
положительный
положительный
Отрицательный/
положительный
положительный
При выполнении анализа выскакивающих вариант было отмечено что большее их количество находится в первой группе, возможно, это связано с неправильной оценкой субъективного показателя ВАШ, также в этой группе наблюдается небольшой процент объяснения исходной изменчивости переменной ВАШ.
При проведении однофакторного дисперсионного анализа для сравнения средних арифметических значений выборок оказалось, что вид инфекции предшествующей реактивному артриту не влияет на показатели активности и ВАШ. На изменение показателей, а именно СОЭ, фибриногена и ВАШ влияет стадия лечения, причем значительные улучшения показателей ВАШ наступают после 2 месяцев лечения, но далее их значения остаются неизменными, а показатели СОЭ и фибриноген изменяются после 3 месяцев лечения.

Нравится материал? Поддержи автора!
Ещё документы из категории математика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ