МОСКОВСКАЯ АКАДЕМИЯ ЭКОНОМИКИ И ПРАВА

РЯЗАНСКИЙ ФИЛИАЛ

КОНТРОЛЬНАЯ РАБОТА

По курсу: «ПРИКЛАДНАЯ МАТЕМАТИКА»

Выполнил: ст-т гр. ЭБ - 241

Лебедев Н. В.

Проверил: профессор

Г. И. Королев

Рязань 2003 г.

Задание 1. Решите, используя формулу полной вероятности, формулу гипотез и формулу Бернулли.

1. Число грузовых автомобилей, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу проезжающих легковых автомобилей как 3:2. Вероятность того, что будет заправляться грузовой автомобиль, равна 0.1. Для легковой автомашины эта вероятность равна 0.2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это легковой автомобиль.

Решение.

Определим событие, вероятность которого надо посчитать. А - к бензоколонке подъехал автомобиль.

Тогда гипотезы:

Н1- к бензоколонке подъехала грузовая машина.

Н2 - к бензоколонке подъехал легковой автомобиль

Р(Н1) = 3/(2+3) = 0.6;

Р(Н2) = 2/(2+3) = 0.4

По условию

Р(А/Н1)=0.1

Р(А/Н2)=0.2

Тогда вероятность события А вычисляется по формуле:

P(A)=Р(A|Н1)*Р(Н1)+Р(A|Н2)*Р(Н2)= 0.6 0.1 + 0.4 0.2 = 0.06 + 0.08 = 0.14

P(H2|A)=[ Р(A|Н2)*Р(Н2) ]/P(A) = 0.2 0.4/ 0.14 ~ 0.57

2. Вероятность своевременной оплаты счетов шестью потребителями равна 0.8. Найти вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.

Решение.

«Оплатят не более трех потребителей», это значит, что возможны следующие варианты событий:

счета оплатят 0 – потребителей,

1 - потребитель,

2 - потребителя,

3 – потребителя.

По формуле Бернулли найдем вероятность каждого из этих событий.

P_n(k) = C_n(k) p^k (1-p)^(n-k), где C_n(k) =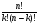

n = 6, p = 0.8

1. C_6(0) = 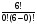= = 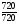1

P_6(0) = C_6(0) 0.8⁰ (1-0.8)^(6-0) = 1 1 0.2⁶ = 0.000064

2. C_6(1) = 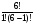= = 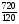6

P_6(1) = C_6(1) 0.8¹ (1-0.8)^(6-1) = 6 0.8 0.2⁵ = 0.001536

3. C_6(2) = 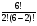= = 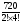= 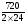15

P_6(2) = C_6(2) 0.8² (1-0.8)^(6-2) = 15 0.64 0.2⁴ = 0.01536

4. C_6(3) = 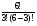= = 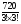= 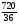20

P_6(3) = C_6(3) 0.8³ (1-0.8)^(6-3) = 20 0.512 0.2³ = 0.08192

P = P_6(0) + P_6(1) + P_6(2) + P_6(3) = 0.000064 + 0.001536 + 0.01536 + 0.08192 = = 0. 09888 0.099 - вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.

Задание 2. Найти среднее квадратическое отклонение вариационного ряда.

X₁ 800 1000 1200 1400 1600 1800 2000

n₁ 1 8 23 39 21 6 2

Среднее квадратическое отклонение случайной величины Xвычисляется по формуле _x = 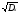, где 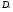– дисперсия случайной величины X.

=

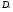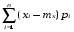
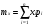- математическое ожидание случайной величины X.

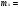800 1 + 1000 8 + 1200 23 + 1400 39 + 1600 21 + 1800 6 + 2000 2 = 139400

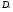= (800 - 139400) 1 + (1000 - 139400) 8 + (1200 - 139400) 23 + (1400 - -139400) 39 + (1600 - 139400) 21 + (1800 - 139400) 6 + (2000 - 139400) 2 =

= 19209960000 + 153236480000 + 439282520000 + 742716000000 + 398765640000 + + 113602560000 + 37757520000 = 1904570680000

_x = 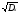1380062

Задание 3. Решить задачу линейного программирования симплексным методом.

Для производства двух видов изделий используются три вида сырья, запасы которого ограничены. Величины запасов приведены в матрице С. Нормы расхода сырья каждого вида на каждое из двух изделий приведены в матрице А , где строки соответствуют виду сырья, а столбцы – виду изделия. Прибыль от реализации изделий указана в матрице P.

Составить план производства изделий так, чтобы предприятие получило максимальную прибыль от их реализации.

5 9 7710

А = 9 7 C = 8910 P = ( 10 22 )

3 10 7800

Найдем производственную программу, максимизирующую прибыль L=10х₁+22х₂.

Затраты ресурсов 1-го вида на производственную программу 5х₁+9х₂≤7710.

Затраты ресурсов 2-го вида на производственную программу 9х₁+7х₂ ≤8910.

Затраты ресурсов 3-го вида на производственную программу 3х₁+10х₂ ≤7800.

Имеем

5х₁+9х₂ ≤ 7710

9х₁+7х₂ ≤ 8910

3х₁+10х₂ ≤ 7800

где по смыслу задачи х₁≥0, х₂≥0.

Получена задача на нахождение условного экстремума. Для ее решения систему неравенств при помощи дополнительных неизвестных х₃, х₄, х₅ заменим системой линейных алгебраических уравнений

5х₁+9х₂+х₃ = 7710

9х₁+7х₂+х₄ = 8910

3х₁+10х₂+х₅= 7800

где дополнительные переменные имеют смысл остатков соответствующих ресурсов, а именно

х₃ – остаток сырья 1-го вида,

х₄ – остаток сырья 2-го вида,

х₅ – остаток сырья 3-го вида.

Среди всех решений системы уравнений, удовлетворяющих условию неотрицательности

х₁≥0, х₂≥0, х₃≥0, х₄≥0, х₅≥0, надо найти то решение, при котором функция L=10х₁+22х₂ будет иметь наибольшее значение.

Ранг матрицы системы уравнений равен 3.

5 9 1 0 0

А = 9 7 0 1 0

3 10 0 0 1

Следовательно, три переменные (базисные) можно выразить через две (свободные), т. е.

х₃ = 7710 - 5х₁ - 9х₂

х₄ = 8910 - 9х₁- 7х₂

х₅= 7800 - 3х₁ - 10х₂

Функция L = 10х₁+22х₂ или L - 10х₁ - 22х₂ = 0 уже выражена через эти же свободные переменные. Получаем следующую таблицу.

Таблица 1.

Базисные переменные

Свободные

члены

х₁

х₂

х₃

х₄

х₅

х₃

7710

5

9

1

0

0

х₄

8910

9

7

0

1

0

х₅

7800

3

10

0

0

1

L

0

-10

-22

0

0

0

Находим в индексной строке отрицательные оценки. Выбираем разрешающий элемент.

В результате получаем следующую таблицу.

Таблица 2.

Базисные переменные

Свободные

члены

х₁

х₂

х₃

х₄

х₅

х₃

7710

5

9

1

0

0

х₄

990

1

7/9

0

1/9

0

х₅

7800

3

10

0

0

1

L

0

-10

-22

0

0

0

Таблица 3.

Базисные переменные

Свободные

члены

х₁

х₂

х₃

х₄

х₅

х₃

2760

0

46/9

1

-5/9

0

х₁

990

1

7/9

0

1/9

0

х₅

4830

0

69/9

0

-1/3

1

L

9900

0

-128/9

0

10/9

0

Таблица 4.

Базисные переменные

Свободные

члены

х₁

х₂

х₃

х₄

х₅

х₂

540

0

1

9/46

-5/46

0

х₁

570

1

0

-7/46

9/46

0

х₅

690

0

0

-3/2

1/2

1

L

17580

0

0

128/46

-10/23

0

Таблица 5.

Базисные переменные

Свободные

члены

х₁

х₂

х₃

х₄

х₅

х₂

690

0

1

-3/23

0

10/46

х₁

300

1

0

10/23

0

-81/46

х₄

1380

0

0

-3

1

2

L

18780

0

0

34/23

0

20/23

Поскольку в индексной строке нет отрицательных оценок, то это значит, что мы получили оптимальную производственная программу:

х₁ = 300, х₂ = 690, х₃ = 0, х₄ = 1380, х₅ = 0

Остатки ресурсов:

Первого вида – х₃=0;

Второго вида – х₄=1380;

Третьего вида – х₅=0

Максимальная прибыль L_max=18780.