Часть А

Задачи, оцениваемые в 3 балла

5

5

5

5

5

5

5

5

1. Любую из восьми пятёрок можно перенести в любую

свободную клетку квадратной таблицы 4х4. Их надо

расположить так, чтобы в каждой строчке и каждом

столбце сумма цифр составляла по 10. Какое наимень-

шее число пятёрок нужно перенести?

а) 4; б) 3; в) 2; г) 1; д) 0.

2. Арбуз и две дыни весят 9кг. Арбуз на 1кг легче двух дынь. Сколько весит

арбуз?

Ответ ____________________________________

3. В магазин привезли 3 одинаковые полные коробки: в одной – груши,

в другой – яблоки, в третьей – вишни. В какой коробке наибольшее

число плодов? Ответ обоснуйте.

Ответ _________________________________________________________

______________________________________________________________

______________________________________________________________

4. Какое из чисел обладает такими свойствами: все его цифры различны,

число сотен в два раза больше числа единиц, а число тысяч в два раза

меньше числа десятков?

а) 1326; б) 3468; в) 3683; г) 4874; д) 3462.

1360

–

290

=

2014

–

5. Бабочка села на записанное в тетради

верное равенство. Какое число она

закрыла?

Ответ __________________________________

6. Квадрат разрезали на 3 кусочка. Два из них изображены

на рисунке справа. Укажите третий кусочек.

а) б) в) г) д)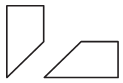

7. В летнем лагере «Орлёнок» Петя решал по 5 задач в день, а Серёжа

на одну задачу меньше, чем Петя. Петя решил все задачи за 4 дня.

За сколько дней решил эти же задачи Серёжа?

Ответ __________________________________

Часть В

Задачи, оцениваемые в 4 балла

8. На столе лежала коробка с конфетами. Саша взял оттуда половину

конфет, потом половину оставшихся конфет взял Коля. Затем Света

взяла из коробки половину того, что там было. После этого осталось

3 конфеты. Сколько конфет было в коробке сначала?

Ответ __________________________________

9. У Маши было 9 кусочков бумаги. Некоторые она разрезала на три части.

Всего получилось 15 кусочков. Сколько кусочков разрезала Даша?

Ответ __________________________________

10. Пять карточек с цифрами лежат на столе в таком

порядке: 5, 1, 4, 3, 2. За один ход разрешается

поменять местами любые две карточки. За какое

наименьшее число ходов можно расположить их

в порядке: 1, 2, 3, 4, 5.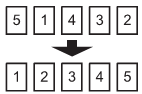

Ответ __________________________________

11. Царь Кащей подобрел и решил потратить 50 золотых монет на подарки

детям. В сундуке у него хранится 5 ларцов, в каждом ларце по 3 шкатулки,

а в каждой шкатулке по 10 золотых монет. Сундук, ларцы и шкатулки

заперты на замки. Какое наименьшее число замков потребуется открыть

Кащею, чтобы достать 50 монет?

Ответ __________________________________

№ задания

1

2

3

4

5

6

7

8

9

10

11

Всего баллов

Количество баллов

Место для решения

Место для штампа

ШКОЛЬНАЯ ОЛИМПИАДА

МАТЕМАТИКА 5кл

________________________________________________

^{Фамилия и имя}