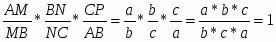
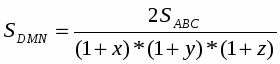
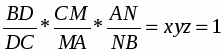
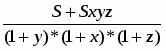
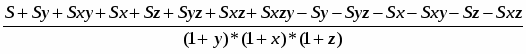
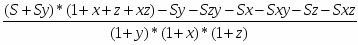
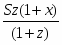
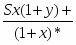
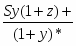
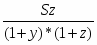
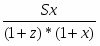
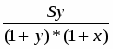
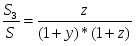
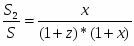
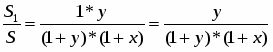
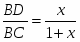
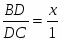
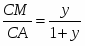
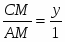
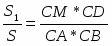
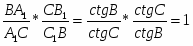
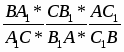
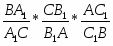
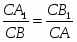
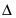
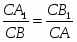
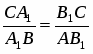
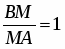
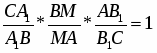
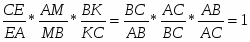
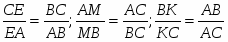
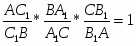
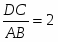
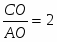
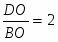
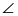
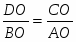
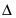
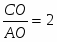
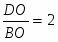
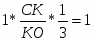
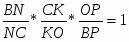
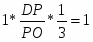
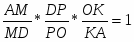
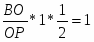
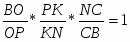
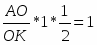
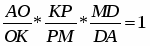
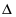
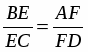
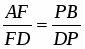
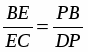
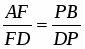
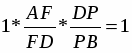
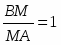
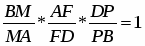
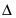
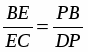
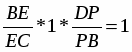
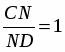
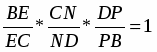
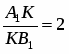
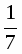
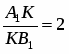
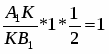
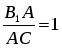
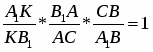
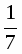
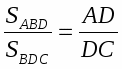
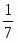
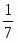
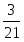
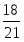
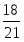
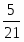
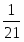
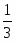
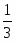
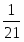
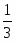
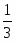
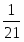
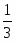
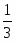
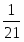
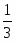
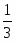
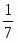
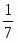
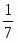
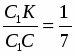
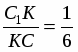
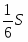
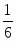
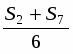
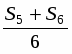
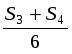
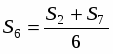
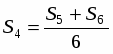
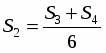
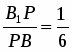
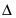
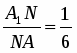
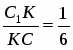
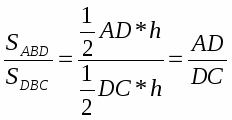
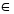
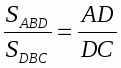
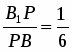
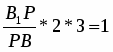
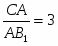
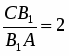
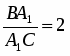
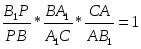
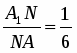
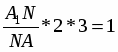
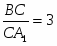
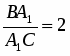
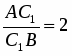
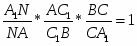
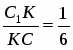
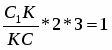
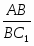
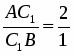
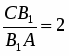
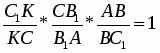
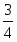
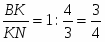
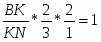
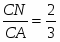
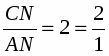
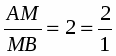
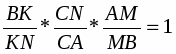
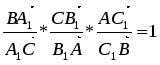
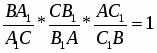
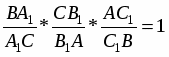Тема: Теорема Менелая. Теорема Чевы. (2 часа)

Цели урока:

1. обобщить, расширить и систематизировать знания и умения учащихся; научить использовать знания при решении сложных задач;

2. способствовать развитию навыков самостоятельного применения знаний при решении задач;

3. развивать логическое мышление и математическую речь учащихся, умение анализировать, сравнивать и обобщать;

4. воспитывать у учащихся уверенность в себе, трудолюбие; умение работать в коллективе.

Задачи урока: 

• Образовательная: изучить теоремы Менелая и Чевы; применить их при решении задач.

• Развивающая: учить выдвигать гипотезу и умело доказательно отстаивать свое мнение; проверить умение обобщать и систематизировать свои знания.

• Воспитательная: повысить интерес к предмету и подготовить к решению более сложных задач.

Ход урока 

I этап. Организационный момент (1 мин.)

Учитель сообщает тему и цель урока.

II этап. Лекция

Чева Джованни (1648-1734 гг.) – итальянский инженер – гидравлик и геометр. Теорема, носящая его имя, опубликована в 1678 году.

Менелай Александрийский (1 – 2 вв. н.э.) – греческий математик и астроном.

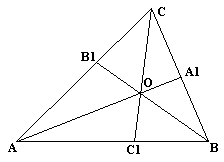
Теорема Менелая. Если прямая пересекает стороны или продолжения сторон BC, CA и AB треугольника ABC соответственно в точках A₁, B₁, C₁, то имеет место равенство

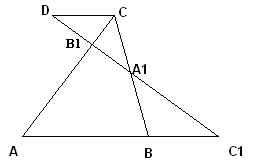
Теорема Чевы

Теорема. Пусть на сторонах BC; CA; AB треугольника ABC или их продолжениях взяты соответственно точки A₁; B₁; C₁. Прямые AA₁; BB₁; CC₁ пересекаются в одной точке или параллельны тогда и только тогда, когда

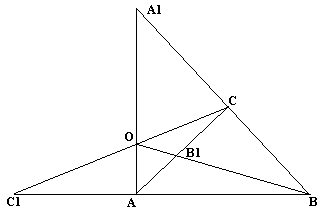
Для решения задач чаще применяется обратная теорема.

Обратная теорема Чевы. Пусть на сторонах BC; CA; AB треугольника ABC или их продолжениях взяты соответственно точки A₁; B₁; C_1. Если выполняются равенство , то прямые AA₁; BB₁; CC₁ пересекаются в одной точке или параллельны.

III этап. Решение задач. (22 мин.)

. Рассмотрим задачи на применение теоремы Менелая.

CMBN = K, MAB, N AC

Найти:

Задача №1

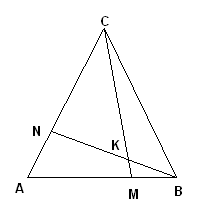
Решение

Рассмотрим 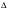ABN и секущую CM (точки пересечения M, K, C). По теореме Менелая: . т.к. , , тогда , то , следовательно,

Ответ: =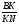

Задача №2

A₁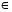BC; B₁ 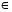AC;

C₁ AB. S_ABC= S,

PKNограничен прямыми:AA₁, BB₁, CC₁.

Найти: S_PKN

Решение

1 способ

Рассмотрим 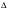ACC₁ и секущую BB₁ (точки пересечения B₁, K, B). Применим теорему Менелая .

; из этого следует =3. Подставим в равенство

, отсюда,

Рассмотрим ABA₁ и секущую CC₁ (Точки пересечения C₁, N, C) По теореме Менелая:

; , отсюда, , подставим в равенство, , отсюда,

Рассмотрим BB₁C и секущую AA₁ (точки пересечения A, P, A₁) По теореме Менелая:

; , отсюда, . Подставим в равенство , отсюда,

Далее будем использовать свойство площадей частей треугольника

, где DAC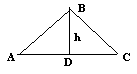

Действительно,

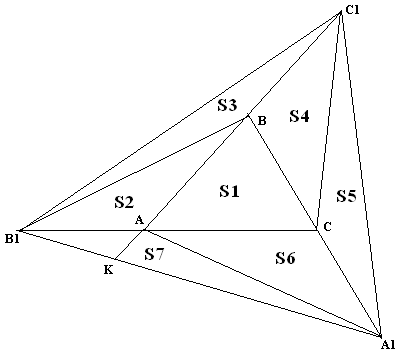
Обратимся к рисунку к задаче

В C₁BC, следовательно, S₃+S₄=6S₂

В AA₁C, следовательно, S₅ +S₆ =6S₄

В ABB₁, следовательно, S₂+S₇=6S₆.

т.к. BA₁ = 2 A₁C, следовательно, S_ABA1 = 2S_AA1C, следовательно, S₁+S₂+S₃+S₇=2S₆+2S₅+2S₄ (1)

т.к. AC₁ = 2BC₁, следовательно, S_ACC1 = 2S_BCC1, следовательно, S₁+S₅+S₆+S₇=2S₂+2S₃+2S₄ (2)

т.к. S_B1BC = 2S_ABB1 (B₁C = 2 B₁A)

S₁+S₃+S₄+S₅=2S₂+2S₆+2S₇ (3)

Сложимравенства (1), (2), (3) почленно:

3S₁+S₂+2S₃+S₄+2S₅+S₆+2S₇=4S₂+4S₄+2S₃+2S₅+4S₆+2S₇.

Послеупрощенияполучим:

3S₁=3S₂+3S₄+3S₆; S₁=S₂+S₄+S₆

Из доказанного, что S₃+S₄=6S₂ следует, что , так же и , подставим,

S₁₌ + + т.е. S₁=(S₂+S₃+S₄+S₅+S₆+S₇)=, следовательно, S=7S₁, где S=S_ABC; S₁=S_PKN.

Ответ: S=7S₁

2 способ

По теореме Менелая:, следовательно, .

Значит, S_C1KB = S_C1BC

Аналогично S_AB1P=S_AB1B, S_A1NC=S_ACA1

По условию A₁C=CB, следовательно, S_ACA1=S_ABC, следовательно, S_A1NC=S_ABC

AB₁=AC, следовательно, S_ABB1=S_ABC, следовательно, S_APB1=S_ABC

C₁B=AB, следовательно, S_C1BC=S_ABC, следовательно, S_C1BK=S_ABC

S_ABC=S_ACA1+S_CC1B-S_A1NC+S_APKC1+S_KPN , пусть S_ABC=S.

S=S+S-S+S+S_KPN

S=S+ S_KPN, откуда S_KPN=(1-)S= S; S_KPN=S

Ответ: S_KPN=S

Задача №3

AB=BC₁; A₁BC; BC=CA₁; B₁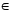AC; AC=AB₁

Найти: а)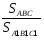

Б) 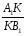, где K=AB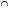A₁B₁

Решение

А) Используем свойство площадей треугольников:

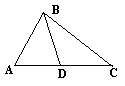
(в случае, если BD –медиана, то S_ABD= S_CBD)

Проведём медианы в B₁AC₁, в B₁A₁C и в BC₁A₁.

ОбозначимплощадичастейA₁B₁C₁буквами S₁;S₂;S₃;S₄;S₅;S₆;S₇

По свойству, приведённому выше:

S₁=S₂ (AB – медианаB₁BC)

S₆=S₇ (A₁A – медианаB₁A₁C) , следовательно, S₁=S₇

S₆=S₁ (AC – медиана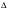ABA₁)

S₂=S₃ (B₁B – медиана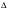AB₁C₁), следовательно, S₁=S₃

S₁=S₄ (CB – медиана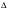ACC₁)

S₄=S₅ (C₁C – медиана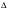BC₁A₁), следовательно, S₁=S₅

S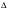_A1B1C1 = S₁+S₂+S₃+S₄+S₅+S₆+S₇ = 7S_ABC, где S_ABC=S₁

Значит, =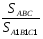

Б) точки A, B, K – лежат на одной прямой, пересекающей стороны 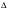A₁B₁C По теореме Менелая: , т.к. B₁A=AC; т.к. BC=CA₁, следовательно, т.е.

Ответ: = ,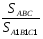

Задача №4

Доказать: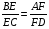

Решение

Используем теорему Менелая для BCD и секущей EP.

; CN=ND; следовательно, .

, следовательно, .

Рассмотрим ABD и секущую MP. По теореме Менелая: ; BM=MA, следовательно, , тогда, , следовательно, .

Из двух равенств: и , следует что, . Что и требовалось доказать.

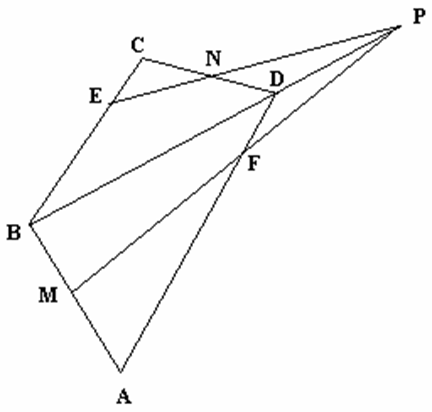
Задача №5

Дано: ABCD – четырёхугольник. M – середина AD; N – середина BC. MP=PK=KN

Доказать: ABCD – трапеция;

DC=2AB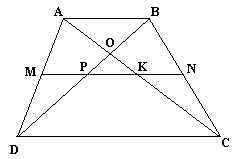

Решение

Используем теорему Менелая поочерёдно к треугольникам:

AKM и секущая DO (точки пересечения O, P, D) ; , следовательно, AO=2OK.

BPN и секущая OC (точки пересечения O, K, C) ; , следовательно, BO=2OP.

AOD и секущая AK (точки пересечения M, P, K) ; , следовательно, DP=3PO

BOC и секущая PN (точки пересечения P, K, N) ; , следовательно, CK=3OK.

Значит, DO=4PO; BO=2PO, т.е.

CO=4OK; AO=2OK, т.е. . В AOB и COD ,

AOB = DOC – вертикальные, следовательно, AOB подобенCOD, следовательно BAO=DCO (накрест лежащие при прямых AB и DC и секущей AC), следовательно, AB || DC. Значит, ABCD – трапеция.

Из равенств и видно, что стороны подобных треугольников AOB и COD относятся как , значит или DC=2AB. Что и требовалось доказать.

Рассмотрим задачи на применение теоремы Чевы.

Задача №1

Дано: Треугольник ABC.

Доказать: медианы треугольника пересекаются в одной точке.

Доказательство

Пусть AA₁, BB₁, CC₁ – медианы треугольника ABC.

Проверим равенство: , 1*1*1=1 (верно).

Утверждение доказано согласно теореме Чевы.

Задача №2

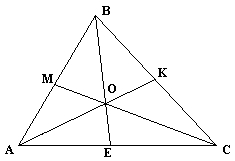
Доказательство

Пусть BE, CM, AK – биссектрисы ABC.

Воспользуемся свойством: биссектриса треугольника делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.

Значит, . Найдём произведение , по теореме Чевы прямые BE, CM, AK пересекаются в одной точке.

PCM, AP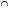BC=A₁, BPAC=B₁

Доказать: A₁B₁|| AB

Задача №3

Решение

Прямые AA₁, BB₁ и CM пересекаются в одной точке P. По теореме Чевы: , , поэтому =>

CB₁A₁ подобен CAB (; C – общий)

Значит, CB₁A₁ = CAB – соответственные при прямых B₁A₁ и AB и секущей AC, поэтому A₁B₁ || AB. Что и требовалось доказать.

Доказать: PAA₁

Задача №4

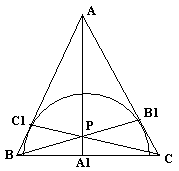
Решение

Пусть r – радиус окружности.

Из прямоугольных треугольников OBC₁ и OCB₁ находим CB₁=r*ctgC, C₁B=r*ctgB.

Из прямоугольных треугольников ABA₁ и ACA₁ имеем BA₁=AA₁*ctgB; A₁C=AA₁*ctgC; AB₁=AC₁ – как отрезки касательных, проведённых из одной точки.

Найдём произведение:

= =

Согласно теореме Чевы прямые AA₁, BB₁, CC₁ пересекаются в одной точке, т.е. PAA₁. Что и требовалось доказать.

Задача №5

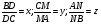
Доказать:

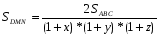
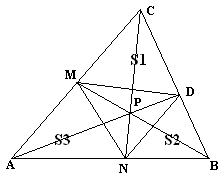
Решение

Пусть S_CDM=S₁, S_BDN=S₂, S_ANM=S₃, S_ABC=S.

Знаем, что площади двух треугольников, имеющих общий угол, относятся как произведения сторон, заключающих этот угол. Имеем

По условию , следовательно ; , следовательно, , отсюда,

Аналогично, ;

Найдём _SDMN = S- (S₁+S₂+S₃)

S_DMN = S-(++)=

=S-==

== =

В треугольнике ABCотрезки AD, BM, CN пересекаются в одной точке. По теореме Чевы

Значит, Что и требовалось доказать.

Задача №6

Доказать. Что отрезки, соединяющие вершины треугольника с точками, в которых вписанная окружность касается противоположных сторон, пересекаются в одной точке.

OM=ON=OP=r

Доказать: AN; BP, CMпересекаются в одной точке.

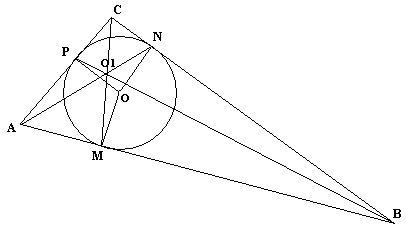
Решение

По свойству отрезков касательных, проведённых из одной точки AM=AP=a; BM=BN=b; CN=CP=c.

Найдём произведение отношений:

По теореме Чевы ANBPCM=O₁

V этап. Итог урока

VI этап. Домашнее задание

1. В треугольнике АВС, площадь которого равна 6, на стороне AB взята точка К, делящая эту сторону в отношении АК:BK = 2:3, а на стороне АС – точка L, делящая АС в отношении AL:LC = 5:3. Точка Qпересечения прямых СК и BL удалена от прямой AB на расстоянии . Найдите длину стороны АВ. (Ответ: 4.)

2. На стороне АС в треугольнике АВС взята точка К. АК = 1, КС = 3. На стороне АВ взята точка L. AL:LВ = 2:3, Q – точка пересечения прямых ВК и СL.  Найдите длину высоты треугольника АВС, опущенной из вершины В. (Ответ: 1,5.)