ВЕРОЯТНОСТЬ ВОКРУГ НАС

Захарова А.В., учащаяся 9 Б класса

Руководитель Ференчук Л.В., учитель математики

МБОУ СОШ №12 с УИОП

«Предвидеть — значит управлять.»

Блез Паскаль

Введение

Мы не раз слышали или сами говорили «это возможно», «это не возможно», «это обязательно должно случаться», «это маловероятно» Такие выражения обычно употребляют, когда говорят о возможности наступления события, которое в одних и тех же условиях может произойти, а может и не произойти. Как наука теория вероятности зародилась в 17 в. Еще в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. Меня заинтересовала эта тема, так возникла моя исследовательская работа «Вероятность вокруг нас».

Я считаю эту тему актуальной по ряду причин:

1. Случай, случайность – с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная ошибка. Казалось бы, тут нет места для математики, – какие уж законы в царстве Случая? Но и здесь наука обнаружила интересные закономерности. Они позволяют человеку уверенно чувствовать себя при встрече со случайными событиями.

2. Теория вероятностей используется в области социально-экономических явлений, а так же необходима при решении многих технических задач.

3. Серьёзный шаг в жизни каждого выпускника основной школы – Государственная итоговая аттестация (ГИА), успешная его сдача - это дело случая? Или….

Цель моего исследования заключалась в следующем:

1) Знакомство с понятием теория вероятности, общими формулами и правилами; применении ее в различных сферах жизнедеятельности человека.

2) Исследование вероятности успешной сдачи учащимися 9 классов ГИА по математике.

Для этого я поставила перед собой задачи:

1) Воспользовавшись различными источниками информации собрать, изучить и систематизировать материал о теории вероятностей.

2) Рассмотреть использование теории вероятности в различных сферах жизнедеятельности.

3) Провести исследование по определению вероятности получения положительной оценки при сдаче ГИА путем угадывания правильного ответа там, где это возможно.

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. Вероятность наступления достоверного события характеризуется как стопроцентная, а вероятность наступления невозможного события характеризуется как нулевая.

• Достоверное событие – событие, которое в данном опыте обязательно наступит.

• Случайное событие – событие, которое в данном опыте может наступить, а может и не наступить.

• Невозможное событие – событие, которое в данном опыте наступить не может.

• Равновероятные события – это события, которые при данных условиях имеют одинаковые шансы для наступления.

А как подсчитать вероятность случайного события? Ведь если случайное, значит, не подчиняется закономерностям, алгоритмам. Оказывается, и в мире случайного действуют определенные законы, позволяющие вычислять вероятности.

Формулы

Принято вероятность события обозначать буквой Р

1. Формула для вычисления вероятности записывается так: P=m/n

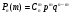2. Формула Бернулли:

Правила

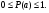1)

2) Для достоверного события m=n и P(a)=1.

3) Для невозможного события m=0 и P(a)=0.

Чтобы найти каковы шансы наступления события А в данной ситуации , необходимо:

• найти общее количество исходов этой ситуации

• найти количество возможных исходов, при которых произойдёт событие А

• найти ,какую часть составляют возможные исходы от общего количества исходов.

Теория вероятностей — сравнительно молодая ветвь математики. Ее развитие как самостоятельной науки началось с переписки Паскаля и Ферма в 1654 году, хотя значительно раньше этих ученых многие математики занимались задачами, относящимися к азартным играм. Настоящую научную основу теории вероятностей заложил великий математик Якоб Бернулли (1654-1705).

1. Теория вероятностей в жизни

1. Игры в кости

Кости — одна из древнейших игр. Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Разновидности игры предполагают разный подсчёт очков.

2. Коды на ….

- сейфах

- телефонные номера

- пароль в социальных сетях (агент, одноклассники и т.д.)

3. Лотереи

Лотерея - организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Кто из нас не мечтал выиграть в лотерею миллион! Но все мы реалисты, и понимаем, что вероятность такого выигрыша очень мала. Ведь игра в лотерею - это игра с судьбой, попытка поймать удачу; и чем больше выигрыш стоит на кону - тем сильнее ощущения!

4. Карточные игры

Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода).

Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Перед использовании той же колоды в следующей игре карты в ней перемешиваются (перетасовываются).

5. Игровые автоматы

Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. Тут все решает Её величество фортуна.

2. Государственная итоговая аттестация

ГИА – серьёзный шаг в жизни каждого выпускника основной школы, требующий и обдуманного выбора своего будущего, и обобщение знания по предмету, и умения организовать свою работу. Экзаменационные работы по различным предметам имеют свои особенности, но во всех из них встречаются задания с выбором ответа. И среди нерадивых учеников часто возникает вопрос: «А нельзя ли выбрать наугад ответ и при этом получить положительную оценку за экзамен? »

Ответить на этот вопрос можно путем использования элементов теории вероятности. Первая часть ГИА по математике содержит 20 заданий, разделенных на три модуля «Алгебра» - 8 заданий, «Геометрия» - 5 заданий и «Реальная математика» - 7 заданий. Для преодоления минимального порога нужно набрать 8 баллов, причем минимум по 2 балла из геометрии и реальной математики и 3 балла из алгебры. На сайте Д. Гущина «Сдам ГИА» http://xn--80aaicww6a.xn--p1ai/ я подобрала варианты заданий, содержащие по 8 заданий, в которых возможно угадать ответ и провела анализ полученных результатов. Каждое задание имело 4 варианта ответов, один из которых правильный.

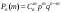Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли.

Схема Бернулли описывает эксперименты со случайным исходом, заключающиеся в следующем. Проводятся n последовательных независимых одинаковых экспериментов, в каждом из которых выделяется одно и тоже событие А, которое может наступить или не наступить в ходе эксперимента. Так как испытания одинаковы, то в любом из них событие А наступает с одинаковой вероятностью. Обозначим ее р = Р(А). Вероятность дополнительного события обозначим q. Тогда q = P(Ā) = 1-p

Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании первой части.

Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда p=P(A)=1/4, а q=P(Ā)=1-p=3/4.

Вероятность получения положительной оценки:

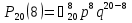
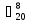= 20•99…•14•13 / 8! = 125970

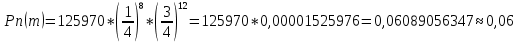
Т.е. вероятность благополучного исхода примерно – 6%

Поскольку в экзамене по математике практически отсутствуют задания с выбором ответа, и введены специальные условия по минимальным баллам для каждого модуля, то вероятность получения положительной оценки путём угадывания сводится к нулю. Но можно рассчитать какова вероятность правильных ответов, если ученик сделал не менее 8-ми заданий. Я рассмотрела возможные случаи этих решений по разделам геометрия, реальная математика и алгебра:

Правильно решены 3 задания по алгебре, 2 задания по геометрии и 3 задания по реальной математике.

P=m/n

1) n=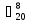==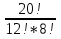125970; 2) m=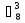**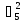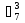=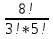**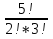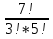=56*10*35=19600

3) P=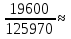0.16 Р=16%

Заключение

В результате проделанной мной работы, я добилась реализации поставленных перед собой целей:

Во-первых, подробно изучила теорию вероятностей.

Во-вторых, исследовала вероятность успешной сдачи учащимися 9 классов ГИА по математике.

В-третьих, я поняла, что теория вероятностей - это целая наука, которой, казалось бы, нет места для математики, – какие уж законы в царстве Случая? Но и здесь наука обнаружила интересные закономерности.

В результате исследования, я сделала вывод: Только планомерная, вдумчивая и добросовестная учеба в школе позволит выпускнику хорошо подготовиться к участию в ГИА, успешно окончить курс основной школы, продолжить обучение в 10 классе или поступить в выбранное профессиональное учебное заведение.