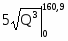
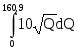
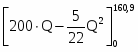
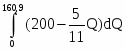
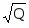
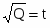
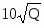
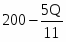
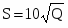
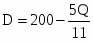
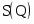
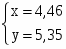
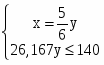
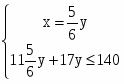
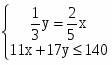
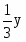
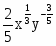
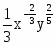
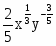
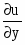
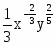
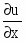
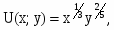
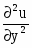
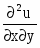
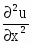
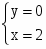
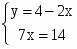
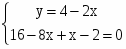
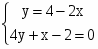
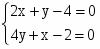
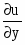
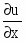
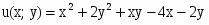
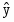
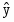
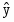
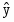
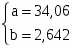
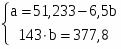
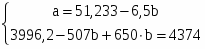
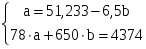
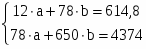
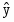
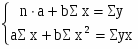
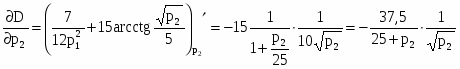
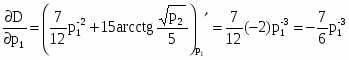
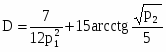
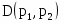
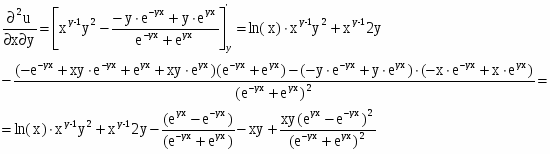
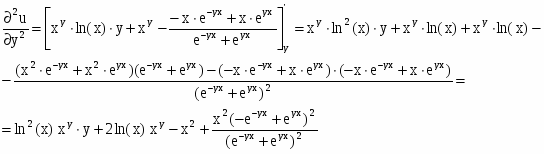
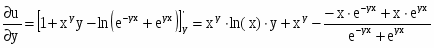
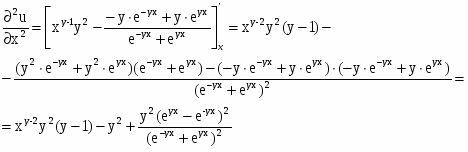
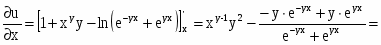
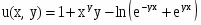
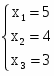
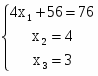
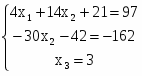
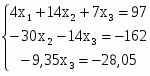
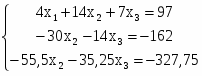
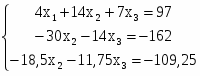
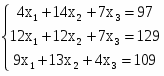
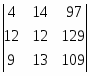
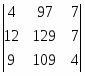
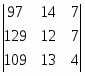
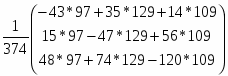
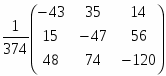
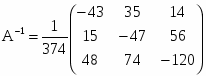
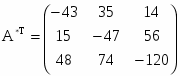
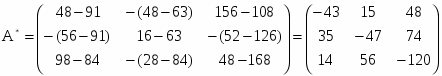
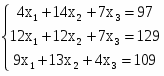
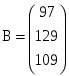
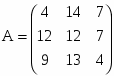План

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задача 7

Задание 8

Литература

Задание 1

Мебельной фабрике для изготовления комплектов корпусной мебели необходимо изготовить их составные части - книжный шкаф, шифоньер, тумба для аппаратуры. Эти данные представлены в таблице:

Наименование составных частей

Виды комплектов корпусной мебели

1

2

3

4

Книжный шкаф

1

1

1

1

Шифоньер

1

1

1

1

Пенал

0

0

1

1

Тумба

0

1

0

1

В свою очередь, для изготовления этих составных частей необходимы три вида сырья - стекло (в кв. м), ДСП (в кв. м), ДВП (в кв. м), потребности в котором отражены в следующей таблице:

Вид сырья

Составные элементы

Кн. шкаф

Шифоньер

Пенал

Тумба

Стекло

0,9

0

0,2

1,2

ДСП

6

6,5

6

2,5

ДВП

2,9

1,7

1,4

0,6

Требуется:

1) определить потребности в сырье для выполнения плана по изготовлению стенок первого, второго, третьего и четвертого вида в количестве соответственно x₁, x_2, x₃ и x₄ штук;

2) провести подсчеты для значений x₁ = 50, x₂ = 30, x₃ = 120 и x₄=80.

Решение: составим условия для определения числа составных частей в зависимости от числа и вида комплектов мебели. Пусть n₁, n₂, n₃ и n₄ - число шкафов, шифоньеров, пеналов и тумб, соответственно.

Тогда условия будут выглядеть следующим образом:

n₁ = x₁ + x₂

n₂ = x₁ + x₂ + x₄

n₃ = x₁ + x₂ + x₃

n₄ = x₁ + x₂ + x₃ + x₄

Составим условия определяющие потребности в сырье в зависимости от вида деталей. Пусть y₁, y₂ и y₃ - потребности в стекле, ДВП и ДСП, соответственно:

y₁ = 0,9n₁ + 0,2n₃ + 1,2n₄

y₂ = 6n₁ + 6,5n₂ + 6n₃ + 2,5n₄

y₃ = 2,9n₁ + 1,7n₂ + 1,4n₃ + 0,6n₄

Теперь подставим вместо n_i - полученные ранее равенства.

y₁ = 0,9· (x₁ + x₂) + 0,2· (x₁ + x₂ + x₃) + 1,2· (x₁ + x₂ + x₃ + x₄)

y₂ = 6· (x₁ + x₂) + 6,5· (x₁ + x₂ + x₄) + 6· (x₁ + x₂ + x₃) + 2,5· (x₁ + x₂ + x₃ + x₄)

y₃ = 2,9· (x₁ + x₂) + 1,7· (x₁ + x₂ + x₄) + 1,4· (x₁ + x₂ + x₃) + 0,6· (x₁ + x₂ + x₃ + x₄)

Приведем подобные

y₁ = 2,3x₁ + 2,3x₂ + 1,4x₃ + 1,2x_4, y₂ = 21x₁ + 21x₂ + 8,5x₃ + 9x₄

y₃ = 6,6x₁ + 6,6x₂ + 2x₃ + 2,3x₄

Проведем подсчеты для значений

x₁ = 50, x₂ = 30, x₃ = 120 и x₄ = 80

y₁ = 2,3 * 50 + 2,3 * 30 + 1,4 * 120 + 1,2 * 80 = 448 кв. м.

y₂ = 21 * 50 + 21 * 30 + 8,5 * 120 + 9 * 80 = 3420 кв. м.

y₃ = 6,6 * 50 + 6,6 * 30 + 2 * 120 + 2,3 * 80 = 952 кв. м.

Задание 2

Пусть a_{ij -} количество продукции j, произведенной предприятием i, а b_{i -} стоимость всей продукции предприятия i исследуемой отрасли. Значения a_ij и b_i заданы матрицами A и В соответственно. Требуется определить цену единицы продукции каждого вида, производимой предприятиями отрасли. В ходе выполнения задания необходимо составить систему уравнений, соответствующую условиям, и решить ее тремя способами (матричный метод, метод Крамера, метод Гаусса).

,

Решение:

Составим систему уравнений:

Матричное уравнение выглядит следующим образом:

A · X = B

Домножим слева каждую из частей уравнения на матрицу A^-1

A^-1 · A · X = A^-1 · B;

E · X = A^-1 · B;

X = A^-1 · B

Найдем обратную матрицу A^-1

Δ = 4 * 12 * 4 + 12 * 7 * 13 + 14 * 7 * 9 - 9 * 12 * 7 - 12 * 14 * 4 - 4 * 7 * 13 = 374

;

X =· = =

Решим систему методом Крамера

Δ = 374

Δ₁ = = 97 * 12 * 4 + 129 * 7 * 13 + 14 * 7 * 109 - 109 * 12 * 7 - 129 * 14 * 4 - 97 * 7 * 13 = 1870

Δ₂ = = 4 * 129 * 4 + 12 * 7 * 109 + 97 * 7 * 9 - 9 * 129 * 7 - 12 * 97 * 4 - 4 * 7 * 109 = 1496

Δ₃ = = 4 * 12 * 109 + 12 * 97 * 13 + 14 * 129 * 9 - 9 * 12 * 97 - 12 * 14 * 109 - 4 * 129 * 13 = 1122

x₁ = Δ_1/Δ = 1870/374 = 5, x₂ = Δ_2/Δ = 1496/374 = 4

x₃ = Δ_3/Δ = 1122/374 = 3

Решим систему методом Гаусса

=> =>

=>

=> =>

Задание 3

Найти частные производные первого и второго порядков заданной функции:

Решение:

Задание 4

Задана функция спроса , где p₁, p₂ - цены на первый и второй товары соответственно.

Основываясь на свойствах функции спроса, определить: какой товар является исследуемым, а какой альтернативным и эластичность спроса по ценам исследуемого и альтернативного товаров.

В процессе решения отметить, какими являются данные товары - взаимозаменяемыми или взаимодополняемыми.

Решение:

Эластичность спроса по цене равна первой производной от функции спроса:

эластичность отрицательная, следовательно, первый товар - исследуемый.

эластичность отрицательная.

Товары являются товарами дополнителями, т.к рост цен на второй товар, как и рост цен на первый товар приводит к снижению спроса.

Задание 5

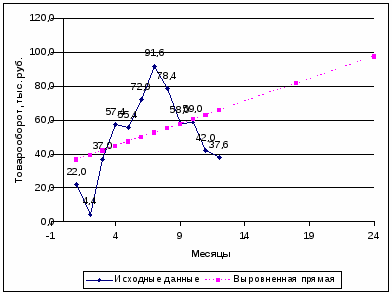
В таблице приведены данные о товарообороте магазина за прошедший год (по месяцам). Провести выравнивание данных по прямой с помощью метода наименьших квадратов. Воспользовавшись найденным уравнением прямой, сделать прогноз о величине товарооборота через полгода и год. Сопроводить задачу чертежом, на котором необходимо построить ломаную эмпирических данных и полученную прямую. Проанализировав чертеж, сделайте выводы.

Месяц

1

2

3

4

5

6

7

8

9

10

11

12

Товарооборот, (тыс. р)

22

4,4

37

57,4

55,4

72

91,6

78,4

58

59

42

37,6

Решение:

Рассчитаем параметры уравнения линейной парной регрессии.

Для расчета параметров a и b уравнения линейной регрессии у = а + bx решим систему нормальных уравнений относительно а и b (она вытекает из метода наименьших квадратов):

По исходным данным рассчитываем х, у, ух, х², у².

t

y

x

yx

x²

y²

1

22,0

1

22,0

1

484,00

36,688

2

4,4

2

8,8

4

19,36

39,332

3

37,0

3

111,0

9

1369,00

41,976

4

57,4

4

229,6

16

3294,76

44,62

5

55,4

5

277,0

25

3069,16

47,264

6

72,0

6

432,0

36

5184,00

49,908

7

91,6

7

641,2

49

8390,56

52,552

8

78,4

8

627,2

64

6146,56

55, 196

9

58,0

9

522,0

81

3364,00

57,84

10

59,0

10

590,0

100

3481,00

60,484

11

42,0

11

462,0

121

1764,00

63,128

12

37,6

12

451,2

144

1413,76

65,772

Итого

614,8

78

4374

650

37980,16

614,76

;

;

Уравнение регрессии: = 34,06 + 2,642 · х

Рассчитаем по данному уравнению значения для и запишем их в дополнительный столбец исходных данных. Найдем прогноз на полгода вперед:

= 34,06 + 2,642 * 18 = 81,636 тыс. руб.

Найдем прогноз на год вперед:

= 34,06 + 2,642 * 24 = 97,5 тыс. руб.

Полученные графики говорят о плохом отражении исходных данных уравнением прямой. Возможно это связанно с наличием сезонности в товарообороте. Тогда прямая линия является уравнением тренда.

Задание 6

Исследовать на экстремум следующую функцию:

;

Решение:

Найдем первые частные производные и определим точки потенциальных экстремумов (там где производные равны нулю).

= 2x + y - 4; = 4y + x - 2;

;

Найдем вторые производные и их значения в точке (2; 0)

= 2 = А, = 1 = B

= 4 = C, Δ = AC - B² = 2 * 4 - 1 = 7

Т.е. в точке (2; 0) имеется экстремум.

Т.к. А > 0, то точка (2; 0) минимум функции.

Задача 7

Пусть функция полезности задана как

где x и y - количество товаров А и В, приобретаемых потребителем, а значения функции полезности численно выражают меру удовлетворения покупателя. При данной стоимости единицы товаров А и В, общая сумма, выделяемая покупателем на их покупку, составляет 140 рублей. При каком количестве товаров А и В полезность для потребителя максимальна. А = 11, В = 17.

Решение:

Полезность максимальна при равенстве первых производных:

= ; = ; = ; =

Ограничение стоимости задается неравенством 11x + 17y ≤ 140

Составим систему.

;

Максимальная полезность будет достигнута при потреблении 4,46 ед. А и 5,35 ед.в.

Задание 8

Заданы функции спроса и предложения в зависимости от количества товара Q: и . Под функциями спроса и предложения будем понимать функциональную зависимость цены от количества товара на рынке. Определить излишки потребителя и излишки производителя при равновесном состоянии спроса и предложения.

и ,

Решение: найдем равновесное состояние спроса и предложения:

D (Q) = S (Q); = ;- t² - 10t + 200 = 0

t₁ = - 34,685 и t₂ = 12,685, t₁ - не удовлетворяет условию

=12,685; Q = 160,9 ед.

При этом цена составит: Р = 10 * 12,685 = 126,85 ден. ед.

Излишки потребителя равны площади фигуры ограниченной сверху кривой спроса, снизу равновесной ценой и слева нулевым выпуском. Найдем излишки потребителя:

S_потр = - 126,85 · 160,9 = - 20410,165 =

= 200 * 160,9 - 5/22 * 160,9 - 20410,165 = 11733,27 ден. ед.

Излишки производителя равны площади фигуры ограниченной сверху равновесной ценой, слева нулевым выпуском и снизу кривой предложения. Найдем излишки производителя:

S_произв = 126,85 · 160,9 - = 20410,165 - =

= 20410,165 - 5 * 12,685³ = 10204,5 ден. ед.

Литература

1.Н.Ш. Кремер. Высшая математика для экономистов. - М.: Банки и биржи, ЮНИТИ, 1997.

2.Н.Ш. Кремер. Практикум по высшей математике для экономистов. - М.: ЮНИТИ-ДАНА, 2007.

3.И.А. Зайцев. Высшая математика. -М.: Высшая школа, 1998.

4.Математический анализ и линейная алгебра. Учебное методическое пособие. Под ред. Н.Ш. Кремера. - ВЗФЭИ, 2006.