«Самостоятельная работа

на уроках математики».

Подготовила:

Учитель математики

Маринкевич Наталья Владимировна

Оглавление

Введение ……………………………………………………..

3

Глава 1.

Самостоятельная учебная деятельность…………………….

4

1.1.

Что такое самостоятельная работа? …………………………

4

1.2.

Четыре уровня самостоятельной деятельности учащихся….

6

1.3.

Типы самостоятельной работы……………………………….

7

Глава 2.

Виды самостоятельной работы……………………………….

8

2.1.

Обучающие самостоятельные работы.....................................

8

2.2.

Тренировочные самостоятельные работы…………………...

9

2.3.

Закрепляющие и повторительные самостоятельные работы.

10

2.4.

Развивающие и творческие самостоятельные работы………

11

2.5.

Проверочные самостоятельные работы……………………...

11

Глава 3.

Система упражнений и задач…………………………………

11

Глава 4.

Контроль и оценка самостоятельной деятельности учащихся………………………………………………………

13

Литература…………………………………………………….

14

Приложения……………………………………………………

15

Введение.

Современная педагогическая наука приоритетным направлением развития школы определяет гуманистический подход в организации процесса обучения. Ведущим принципом гуманистической модели учебного процесса является развитие личности школьника. Одно из ведущих качеств личности – самостоятельность. Оно выражается в умении ставить перед собой определённые цели и добиваться их достижения собственными силами. Степень развития ученика измеряется и оценивается его способностью самостоятельно приобретать новые знания и использовать их в учебной и практической деятельности. Существующая сегодня система общего образования не носит еще подлинно гуманистический характер. В связи с этим не в полной мере школа способствует развитию и саморазвитию учащихся, готовит к творческому выполнению всех функций в новом обществе.

Среди факторов, способствующих формированию творческой активности учащихся, одно из ведущих мест занимает самостоятельная работа. Только целенаправленная систематическая самостоятельная работа каждого школьника позволяет глубоко усвоить знания, выработать и закрепить умения, превратить их в соответствующие навыки умственного труда.

Изучение математики на базовом уровне среднего (полного) общего образования направлено на достижение следующих целей:

• формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

• развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;

• воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.

Достижение этих целей требует от учителя не простого изложения знаний, в определённой системе, а предполагает также учить школьников мыслить, искать и находить ответы на поставленные вопросы, добывать новые знания, опираясь на уже известные. Учащихся надо целенаправленно учить познавательной деятельности, вооружать их учебно-познавательным аппаратом.

Степень развитости ученика измеряется и оценивается его способностью самостоятельно приобретать новые знания, использовать в учебной и практической деятельности уже полученные знания. Вот поэтому так важно воспитание у учащихся активности и учебной самостоятельности. Обучение не может считаться правильно ориентированным и не может протекать успешно, если не ставится задача вооружения школьников системой умений и навыков учебного труда.

При отсутствии должной роли самостоятельности знания запоминаются учащимися механически, они не обнаруживают того многообразия связей, которое должно быть усвоено для достижения высокого уровня системности знаний. Несмотря на то что вопрос о самостоятельной работе стоит перед школой давно, этот метод обучения не находит и сегодня должного применения. На самостоятельную работу учащихся отводится не более 13 % всего времени урока, причём и это время на уроке малоэффективно.

Проводя ту или иную самостоятельную работу учащихся, учителя рассматривают её как самоцель, не обращая внимания на то, что способствует ли она активной мыслительной деятельности ученика или нет. Часто большое число самостоятельных работ направлено лишь на выполнение заданий по образцу, среди которых мало заданий творческого характера. В то время как задания творческого характера, развивают у учеников умение отойти от той формы изложения материала, которая была предложна учителем или учебником, способствуют более глубокому изучению материала, раскрытию его новых сторон.

Одним из недостатков в методике проведения самостоятельных работ состоит в однообразии их видов, используемых учителем. Абсолютное большинство самостоятельных работ на уроках математики приходится на закрепление изложенного учителем материала непосредственно после его изучения и на проверку знаний учащихся. Значительно меньшее число их используется при изучении нового материала.

Цель этой работы – рассмотреть все виды самостоятельной работы учащихся, классифицировать типы самостоятельных работ по уровням усвоения знаний, привести примеры организации самостоятельной деятельности учащихся на уроках математики.

Глава 1. Самостоятельная учебная деятельность.

1. Что такое самостоятельная работа ?

Одним из самых доступных путей активизации учащихся на уроке является соответствующая организация самостоятельной учебной работы. Она занимает исключительное место на уроке, потому что ученик приобретает знания только в процессе личной учебной деятельности.

На уроке дети должны трудиться по возможности самостоятельно, а учитель – руководить этим самостоятельным трудом, давать для него материал.

Под самостоятельной учебной работой обычно понимают любую организованную учителем активную деятельность учащихся, направленную на выполнение поставленной дидактической цели в специально отведённое для этого время: поиск знаний, их осмысление, закрепление, формирование и развитие умений и навыков, обобщение и систематизацию знаний. Самостоятельная работа представляет собой, с одной стороны, учебные задания, то есть то, что должен выполнить ученик, объект его деятельности, с другой – форму проявления соответствующей деятельности памяти, мышления, творческого воображения при выполнении учеником учебного задания, которое в конечном счёте приводит школьника либо к получению совершенно нового, ранее неизвестного ему знания, либо к углублению и расширению сферы действия уже полученных знаний.

Следовательно, самостоятельная работа – это такое средство обучения, которое

• в каждой конкретной ситуации соответствует дидактической цели и задаче;

• формирует у обучающегося на каждом этапе его движения от незнания к знанию необходимый объём и уровень знаний, навыков и умений для решения определённого класса познавательных задач и соответственного продвижения от низших к высшим уровням мыслительной деятельности;

• вырабатывает у учащихся психологическую установку на самостоятельное систематическое пополнение своих знаний и выработку умений ориентироваться в потоке полученной информации;

• является важнейшим орудием управления самостоятельной познавательной деятельностью в процессе обучения.

В теории и практике обучения наиболее распространены следующие подходы к классификации самостоятельных работ:

• по дидактическим целям:

• по уровню самостоятельности у учащихся;

• по степени индивидуальности;

• по источнику и методу приобретения знаний;

• по форме выполнения;

• по месту выполнения.

По своему дидактическому назначению самостоятельные работы делятся на обучающие (работы по формированию знаний и по формированию умений) и контролирующие.

По степени самостоятельности учащихся выделяют:

1. Самостоятельные работы по образцу. Предлагаемые при этом задания выполняются по алгоритмам и образцам, показанным учителем или подробно описанным учителем. Они имеют особую роль при первичном закреплении изученного, так как способствуют созданию условий для перехода учащихся к выполнению заданий, требующих более высокого уровня самостоятельности. В данном случае учитель требует от учащихся их точного воспроизведения.

2. Реконструктивно-вариативные. Эти работы обычно содержат в себе задачи, по условиям которых учащимся приходится анализировать новые для них ситуации, переформулировать их, выбирать из известных способов наиболее рациональные. Они отличаются от частично-поисковых (эвристических) работ по образцу тем, что при их выполнении необходимо преобразовывать исходные данные, то есть проявить более высокий уровень самостоятельности.

3. Частично-поисковые (эвристические). Ещё более высокий уровень самостоятельности учащиеся проявляют при выполнении частично-поисковых (эвристических) работ, требующих переноса знаний и умений в непривычные, нестандартные ситуации.

4. Исследовательские (творческие) самостоятельные работы. Пользуясь накопленными знаниями и умениями, выдвигая и проверяя собственные гипотезы и суждения, они учатся открывать для себя новые сведения об изучаемых объектах.

Классификация по степени индивидуальности включает общеклассные, групповые и индивидуальные самостоятельные работы. Их проводят, в той или иной мере учитывая индивидуальные особенности каждого ученика, в условиях органического соединения индивидуальной и коллективной деятельности учащихся.

Общеклассные самостоятельные работы бывают фронтальными: когда все учащиеся класса выполняют одни и те же задания. Нередко для всех учащихся класса проводят двух или боле вариантные самостоятельные раборы, идентичные по содержанию. Ныне же всё большее внимание получают дифференцированные самостоятельные работы, соответствующие разному уровню подготовленности учащихся одного и того же класса. Приложение 1.

Самые разнообразные виды самостоятельных работ содержит классификация по источнику и методу приобретения знаний. Наиболее распространенные из них:

• работа с книгой (учебником, справочной литературой и т. д.);

• лабораторные и практические работы;

• подготовка докладов, рефератов и т. д.

По форме выполнения различают устные и письменные самостоятельные работы, а по месту выполнения – классные и домашние.

Успешному выполнению учащимися самостоятельной работы способствую чёткие указания учителя о её цели, содержании, способах выполнения, формах выражения получаемых результатов. Они могу быть представлены виде памяток, в которых даются рекомендации по работе с текстом, написанию докладов, рефератов и т. д.

Содержание, форма и продолжительность самостоятельной работы, проводимой в классе, должны отвечать поставленным целям урока. Нередко она занимает лишь несколько минут (устный счет в 5-6-х классах) или может длиться в течение всего урока (в старших классах).

2. Четыре уровня самостоятельной деятельности учащихся.

Выделяются четыре уровня самостоятельной деятельности учащихся, соответствующие их учебным возможностям.

1. Копирующие действия учащихся по заданному образцу. Узнавание объектов путём сравнения с известным образом. На этом уровне происходит подготовка к самостоятельной деятельности.

2. Репродуктивная деятельность по воспроизведению информации, в основном не выходящая за пределы уровня памяти. На этом уровне уже начинается обобщение приёмов и методов познавательной деятельности, их перенос на решение более сложных, но типовых задач.

3. Продуктивная деятельность самостоятельного применения приобретённых знаний для решения задач, выходящих за пределы известного образца, требующая способности к индуктивным и дедуктивным выводам.

4. Самостоятельная деятельность по переносу знаний при решении задач в совершенно новых ситуациях.

Каждый из этих уровней, хотя они выделены условно, объективно существует. Дать самостоятельное задание ученику уровнем выше – это в лучшем случае напрасно потерять время на уроке.

Рассмотрим основные требования к организации самостоятельной деятельности учащихся на уроке. Любая самостоятельная работа на любом уровне имеет конкретную цель. Каждый ученик знает порядок и приёмы выполнения работы. Самостоятельная работа соответствует учебным возможностям ученика, а степень сложности удовлетворяет принципу постепенного перехода с одного уровня самостоятельности на другой. В учебном процессе используются результаты, выводы самостоятельной, в том числе домашней, работы.

3. Типы самостоятельной работы.

Назначение самостоятельной работы – развитие познавательных способностей, инициативы в принятии решения, творческого мышления. Поэтому, подбирая задания, надо свести к минимуму шаблонное их выполнение. Содержание работы, форма её выполнения должны вызывать интерес учащихся, желание выполнить работу до конца.

По форме организации самостоятельные работы можно разделить на индивидуальные, фронтальные и групповые.

Можно выделить четыре типа самостоятельных работ в соответствии с уровнями самостоятельной деятельности учащихся.

• Воспроизводящие.

• Реконструктивно-вариативные.

• Эвристические.

• Творческие.

Воспроизводящие самостоятельные работы по образцу необходимы для запоминания способов действий в конкретных ситуациях. Деятельность учеников при выполнении работ этого типа не совсем самостоятельная, поскольку их самостоятельность ограничивается простым воспроизведением, повторением действий по образцу. Эти работы формируют фундамент для подлинной самостоятельной деятельности.

Самостоятельные работы реконструктивно-вариативного типа позволяют на основе полученных ранее знаний и данной учителем общей идеи найти самостоятельно конкретные способы решения задачи применительно к данным условиям задания.

Эвристические самостоятельные работы формируют умения и навыки поиска ответа за пределами известного образца. Как правило, ученик сам определяет путь решения задачи и находит его. Знания, необходимые для решения, ученик уже имеет, но отобрать их в памяти бывает нелегко.

Творческие самостоятельные работы являются венцом системы самостоятельной деятельности. Эта деятельность позволяет учащимся получать принципиально новые для них знания, закрепляет навыки самостоятельного поиска знаний. Психологи считают, что умственная деятельность школьников при решении трудных, проблемных задач во многом аналогична умственной деятельности творческих и научных работников.

Глава 2. Виды самостоятельной работы.

Самостоятельную деятельность учащихся можно и нужно организовывать на различных уровнях: от воспроизведения действий по образцу и узнавания объектов путём их сравнения с неизвестным образцом до составления модели и алгоритма действий в нестандартных ситуациях. Необходимо учитывать, что при составлении заданий для самостоятельной работы степень сложности должна отвечать учебным возможностям детей.

Переход с одного уровня на другой осуществляется постепенно, только когда учитель будет убеждён, что учащиеся справятся со следующим уровнем самостоятельности. Иначе в атмосфере спешки и нервозности у ученика возникают пробелы в знаниях.

Очень важно, чтобы содержание самостоятельной работы, форма и время её выполнения отвечали основным целям обучения данной теме на данном этапе.

В то же время учителю нужно знать, что злоупотребление самостоятельной работой в учебном процессе также вредно, как и её недооценка. Бывает так, что учитель включает в урок самостоятельную работу без особой необходимости, просто ради разнообразия, не продумав её содержание и форму организации. Результаты бывают плачевными: или дети не готовы выполнить задание, или не хватило времени т. п. А в результате – зря потрачено драгоценное время. Но если , составляя план урока, учитель тщательно продумал место и время самостоятельной работы, чётко определил её общее содержание, разбил задания по разным уровням сложности, то она сыграет свою положительную роль.

Поэтому учителю очень важно знать формы и виды самостоятельных работ, их место в процессе обучения.

В зависимости от целей, которые ставятся перед самостоятельными работами, они могут быть:

1. обучающими;

2. тренировочными;

3. закрепляющими;

4. повторительными;

5. развивающими;

6. творческими;

7. контрольными (проверочными).

2.1. Обучающие самостоятельные работы.

Смысл обучающих самостоятельных работ заключается в самостоятельном выполнении школьниками данных учителем заданий в ходе объяснения нового материала. Цель таких работ – развитие интереса к изучаемому материалу, привлечение внимания каждого ученика к тому, что объясняет учитель. Здесь сразу выясняется непонятное, выявляются сложные моменты, дают о себе знать пробелы в знаниях, которые мешают прочно усвоить изучаемый материал.

Самостоятельные работы по формированию знаний проводятся на этапе подготовки к введению нового содержания, а также при непосредственном ведении нового содержания, при первичном закреплении знаний, то есть сразу после объяснения нового, когда знания учащихся ещё непрочны. Учителю необходимо знать следующие особенности обучающих самостоятельных работ: их надо составлять в основном из заданий репродуктивного характера, проверять немедленно и не ставить за них плохих оценок.

Так как самостоятельные обучающие работы проводятся во время объяснения нового материала или сразу после объяснения, то их немедленная проверка даёт учителю чёткую картину того, что происходит на уроке, какова степень понимания учащимися нового материала на самом раннем этапе его изучения. Цель этих работ – не контроль, а обучение, поэтому им следует отводить много времени на уроке.

К обучающим самостоятельным работам можно отнести составление примеров на изучаемые правила, свойства. Например, в 9 классе при изучении темы «Разложение квадратного трёхчлена на множители» после объяснения учителя можно предложить следующую самостоятельную работу: «Запишите разложение квадратного трёхчлена, зная его корни». Работа может быть оформлена в виде таблицы. Приложение 2.

Конечно, не все учащиеся сразу смогут поменять знаки перед отрицательными корнями, не все смогут оформить задания так, как требует правило, но для учителя это возможность сразу же указать верный ход решения, пока у ученика ещё не выработался неверный навык.

Самостоятельно составляя примеры на изученные правила и свойства, учащиеся осмысленно их запоминают, учатся применять их, с интересом воспринимают изучаемый материал, так как они сами участвуют в его объяснении.

К обучающим самостоятельным работам относятся также самостоятельное составление алгоритмов, решение задач по алгоритму.

Например, после того как введено понятие неравенства второй степени с одной переменной (алгебра, 9 класс), составляется следующий алгоритм:

1. находят дискриминант квадратного трёхчлена ах² + bх + с и выясняют, имеет ли трёхчлен корни;

2. если трёхчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а > 0 или вниз при а <0; если трёхчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а >0 или в нижней при а <0;

3. находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах² + bх + с > 0) или ниже оси х (если решают неравенство ах² + bх + с < 0).

2.2. Тренировочные самостоятельные работы.

К тренировочным относятся задания на распознавание различных объектов и их свойств. Например: какие из данных графиков являются графиком квадратичной функции? Приложение 3. В тренировочных заданиях часто требуется воспроизвести или непосредственно применить теоремы, определения, свойства тех или иных математических объектов. Тренировочные самостоятельные работы состоят из однотипных заданий, содержащих существенные признаки и свойства данного определения, правила. Конечно, эта работа мало способствует умственному развитию детей, но она необходима, так как позволяет выработать основные умения и навыки и тем самым создать базу для дальнейшего изучения математики.

При выполнении тренировочных самостоятельных работ учащимся ещё необходима помощь учителя. Можно разрешить пользоваться и учебником, и записями в тетрадях, таблицами и т. п. Всё это создаёт благоприятный климат для слабых учащихся, В таких условиях они очень легко включаются в работу и выполняют её.

К таким работам можно отнести выполнение заданий по разноуровневым карточкам. По этим карточкам учащиеся привыкают работать самостоятельно.

Учащиеся получают карточку в зависимости от уровня знаний :

• со знаком треугольника – на «3»;

• со знаком квадрата – на «4»;

• со звёздочкой – на «5».

Некоторые учащиеся, выполнив своё задание, хотят попробовать решить задание более высокого уровня. В таком случае учитель даёт им карточку с соответствующим знаком. Постепенно ученики привыкают не бояться трудностей и стремиться к более высокой самооценке. Приведём пример тренировочной самостоятельной работы по 3 уровням сложности, составленной по теме «Многоугольники».

Приложение 4.

2.3. Закрепляющие и повторительные самостоятельные работы.

К закрепляющим можно отнести самостоятельные работы, которые способствуют развитию логического мышления и требуют комбинированного применения различных правил и теорем. Они показывают, насколько прочно, осмысленно усвоен учебный материал. По результатам проверки заданий данного вида учитель определяет, нужно ли ещё заниматься данной темой. Примеры таких работ в изобилии встречаются в различных дидактических материалах. Приложение 5.

Очень важны так называемые повторительные (обзорные или тематические) работы. Перед изучением новой темы учитель должен знать, подготовлены ли школьники, есть ли у них необходимые знания, какие пробелы могут затруднить изучение нового материала. Например, в курсе алгебры 8 класса перед изучением темы «Сложение и умножение числовых неравенств» целесообразно провести обзорную самостоятельную работу по теме «Свойства числовых неравенств». Приложение 3 .

2.4. Развивающие и творческие самостоятельные работы.

Самостоятельными работами развивающего характера могут быть домашние задания по составлению докладов на определённые темы, подготовка к олимпиадам, научно-творческим конференциям, проведение в школе «дней математики», сочинение математических игр, сказок, спектаклей и другое.

Большой интерес вызывают у учащихся творческие самостоятельные работы, которые предполагают высокий уровень самостоятельности.

Здесь учащиеся открывают для себя новые стороны уже имеющихся у них знаний, учатся применять эти знания в новых неожиданных ситуациях.

Это задания на поиск второго, третьего и т. д. способа решения задачи. Например, для нахождения высоты, опущенной из вершины прямого угла, если известны три элемента данного треугольника, можно применить способы, основанные на следующих фактах: на определении синуса острого угла, на вычислении формулы площади треугольника, на теореме Пифагора и т. д. Приложение 7.

2.5. Проверочные (контрольные) самостоятельные работы.

Контрольные работы являются необходимым условием достижения планируемых результатов обучения.

По существу разработка текстов контрольных работ должна быть одной из основных форм фиксирования целей обучения, в том числе и минимальных. Поэтому, во-первых, контрольные задания должны быть равноценными по содержанию и объёму работы, во-вторых, они должны быть направлены на отработку основных навыков; в-третьих, - обеспечивать достоверную проверку уровня обучения; в-четвёртых, они должны стимулировать учащихся, позволять им продемонстрировать прогресс в своей общей подготовке. Приложение 8.

Глава 3. Система упражнений и задач.

Упражнения и задачи являются наиболее распространённым видом самостоятельной работы по математике. Их роль при осмыслении и закреплении знаний, развитии мышления учащихся исключительно велика. Особенно эффективна продуманная система упражнений, учитывающая индивидуальные возможности ученика, уровень самостоятельности, необходимый для их выполнения.

По целевому назначению упражнения удобно разделить на три группы:

1. Упражнения, составленные для изучения материала, приобретения умений и навыков. Из них выделяют подготовительные, пробные, предназначенные для выполнения действий по образцу, схеме, заданному предписанию и т. д.

2. Упражнения, составленные для закрепления пройденного материала.

3. Контрольные задания, составленные с целью проверки глубины усвоения полученных знаний.

Организация учебной деятельности по решению различных учебных задач включает в себя следующие этапы: анализ содержания поставленной задачи и определение цели действий; поиск плана решения задачи(достижения цели действия); реализация найденного плана; проверка правильности действий, истинности действий; анализ других возможных вариантов решений, доказательств и их сопоставление с первым.

Чёткий план организации действий при выполнении различных упражнений резко увеличивает их эффективность. Часто беспомощность ученика при решении задачи является следствием его методических неумений, а не пробелами в знаниях.

При подборе задач и упражнений по каждой теме особое внимание обращается на всестороннее закрепление всех признаков понятия, чётко выделяются навыки и умения, которые надо сформировать и закрепить с помощью системы различных упражнений. Исключить упражнения «на всякий случай» - значит заметно повысить эффективность урока.

Учитель постоянно следит за точностью выполнения задания, особенно на этапе подготовительных и пробных упражнений, поскольку могут быть закреплены ошибки учеников, их неверные навыки. Не случайно этот этап характеризуется низким уровне самостоятельности.

Систему упражнений и задач удобно организовать по этапам.

• Начинать с типовых задач и заданий. Подробно объясняется метод их решения. Ученики закрепляют его, выполняя действия по образцу.

• Затем даются аналогичные задачи и упражнения с планом решения и оказанием помощи при решении. На этом этапе нужна энергичная коррекция уровня самостоятельности.

• Далее следуют задачи с кратким планом решения или краткими указаниями для выполнения заданий. Контроль на этом этапе особенно важен, хотя уровень самостоятельности уже достаточно высокий. Приложение 9.

• Задачи и упражнения для полностью самостоятельного выполнения. На этом этапе выясняется, достаточно ли подготовлен ученик на предыдущих этапах и способен ли он для творческой работы.

Важная роль в развитии умения решать задачи отводится правильной организации поиска решения любой конкретной задачи. Необходимо значительную часть этой работы алгоритмизировать, создать ряд чётких предписаний для их решения. При этом нельзя позволять формально использовать алгоритмы. Эффективны задачи с недостающими или лишними данными в условии.

Выделим некоторые типичные ошибки в организации и проведении упражнений при самостоятельной деятельности на уроке:

• упражнения бывают случайные, не представляющие собой часть продуманной системы;

• упражнения часто проводятся фронтально, не индивидуализируются;

• ученик не получает своевременно указаний о допущенных ошибках и верных способах действия.

Глава 4. Контроль и оценка самостоятельной деятельности учащихся.

Совместная деятельность учителя и учащихся по освоению программного материала, как и любой другой полноценной деятельности, состоит из ориентировочной (оргмомент, постановка цели, актуализация), исполнительной(сообщение новых знаний, усвоение, применение) и контролирующей частей.

В контролирующей части устанавливается обратная связь в системе «учитель-ученик», позволяющая регулярно получать информацию, используемую для определения качества усвоения учащимися учебного материала, своевременного диагностирования и корректирования их знаний и умений. В ходе контроля выявляются и оцениваются знания и умения учащихся, что даёт возможность получать и накоплять сведения, необходимые для успешного управления их обучением, воспитанием и развитием.

Различают три типа контроля:

• внешний контроль за деятельностью учащихся;

• взаимный контроль учащихся;

• самоконтроль.

Внешний контроль приучает обучающихся добросовестно и систематически выполнять учебную работу, вызывает стремление сделать её лучше, а при целенаправленной работе учителя способствует развитию взаимоконтроля и самоконтроля. При взаимоконтроле вырабатывается более ответственное отношение учащихся к оценке деятельности одноклассников, нежели своей. Проведение самоконтроля направлено на осознание правильности своих действий, на предупреждение или обнаружение уже совершенных ошибок. Приложение 10.

При обучении самоконтролю особое внимание следует уделить ознакомлению и овладению учащимися приёмами проведения контролирующих действий.

Приёмы самоконтроля:

• сверка с образцом (ответом);

• повторное решение задачи, выполнение упражнения;

• проверка полученных результатов;

• использование различных способов вариантов при выполнении задания;

• моделирование;

• примерная оценка искомых результатов;

• проверка на частном случае;

• испытание получаемых результатов о косвенным параметрам.

В основе этой классификации лежит принцип выделения специфики контролирующих действий. При проведении самоконтроля ключевым звеном является сверка с готовым или составленным образцом.

Контроль должен быть целенаправленным, объективным, всесторонним, регулярным и индивидуальным. Его результаты выражаются в оценке, отражающей степень соответствия знаний и умений учащихся программным требованиям. Это соответствие может иметь цифровую или другую символическую форму выражения и фиксации оценки, именуемой отметкой.

Основные подходы к оценке знаний и умений учащихся:

• по ошибкам;

• по «производительности»;

• комбинированный.

Оценивание знаний и умений учащихся по ошибкам осуществляется в зависимости от количества и характера погрешностей, допущенных ими. Оценки по «производительности» формируются с учётом объёма верно выполненной работы. При комбинированном подходе учитываются как ошибки, так и объём выполненной работы.

В практике обучения применяются устный, письменный, лабораторный методы контроля. Они могут осуществляться путём индивидуальной, групповой и фронтальной проверок.

Устный контроль: опрос, устные контрольные работы и т. д.

Приложение 11.

Письменный контроль. Проведение контролирующих самостоятельных работ, диктантов, контрольных, письменных работ, тестов, зачётов и т. д. Приложение 12

Заключение.

Эффективность самостоятельной работы достигается, если она является одним из составных, органических элементов учебного процесса, и для неё предусматривается специальное время на уроке, если она проводится планомерно и систематически, а не случайно и эпизодически. Только при этом условии у учащихся вырабатываются устойчивые умения и навыки в выполнении различных видов самостоятельной работы и наращиваются темпы в её выполнении.

Самостоятельная работа является обязательным компонентом учебно-воспитательного процесса математического образования. Роль, форма, содержание и длительность определяются целью изучения математического материала, его спецификой и уровнем подготовки школьников.

Планируя самостоятельную работу, необходимо:

- предусмотреть её место в структуре урока;

- решить, как она будет сочетаться с другими методами и формами учебной деятельности;

- определить её оптимальный объём в зависимости от уровня подготовленности учеников, а также сложности изучаемого материала;

- предусмотреть затруднения, которые могут возникнуть при выполнении самостоятельной работы;

- определить форму работы и заданий;

- установить оптимальную длительность работы;

- подобрать соответствующий дидактический материал;

- предусмотреть рациональные способы проверки и самопроверки работ

учеников.

Проблема совершенствования методики применения самостоятельной работы является актуальной, так как для овладения современным содержанием школьного математического образования необходимо повысить эффективность процесса обучения при активизации самостоятельной деятельности учащихся.

В обучении математике необходимо с единых позиций выстраивать систему применения самостоятельных работ учащихся, соотнося их с каждым этапом усвоения учебного материала. Успех работы учителя зависит от выявления индивидуальных особенностей учащихся в учебно-познавательной деятельности и их учёт при планировании и организации самостоятельных работ.

Литература.

1. Зотов Ю. Б. Организация современного урока./Зотов Ю. Б. – М. : Просвещение, 1984. – 144с.

2. Кульневыч С. В. Современный урок. Часть 1. /Кульневич С. В., Лакоценина Т. П. – Учитель, 2006. – 288 с.

3. Муравьёв Е. М., Богоявленская А. Е. Формы организации учебных занятий. // Завуч. 1998 № 4.

4. Чередов И. М. Формы учебной работы в средней школе./ Чередов И.М. – М.: Просвещение, 1998.

5. Гиршович В. С. Виды самостоятельных работ. / В. С. Гиршович// Математика в школе. – 1998. - №3. – С. 37-43.

Приложение 1.

Алгебра, 9 класс.

Самостоятельная работа по теме

«РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЁХЧЛЕНА НА МНОЖИТЕЛИ».

1 УРОВЕНЬ

1. Разложите на множители квадратный трёхчлен:

а) х² – 7х + 12; б) 5х² – 5х -10; в) 4х² – 144 = 0;

г) 10х² + 29х – 3; д) х² – 2х - 63; е) 6х² + 5х – 4.

2. Сократите дробь:

а) а² – 4 б) b² – b – 6 в) 7 + 6с – с² г) х³ + х² – 72х

———; ————; ————; —————

7а + 14 9b + 18 21 – 3с 9х – 72

3. Найдите значение выражения:

3х² + 11х – 4

—————— при х = -22.

6х - 2

2 УРОВЕНЬ

1. Найдите корни квадратного трёхчлена:

а) х² + 6х – 16; б) –х² + 2х + 99; в) 2х² + 7х – 4.

2. Выделите квадрат двучлена из квадратного трёхчлена. Закончите решение:

а) х² – 18х + 14 = х² - 2· 9 · х + 9² – 9² + 14 = …;

б) -х² - 24х + 25 = - (х² + 24х – 25) = - (х² + 2 · 12 · х + 12² – 12² – 25) = …;

в) -х² + 6х = - (х² – 6х) = - (х² – 2 · 3 · х + 3² – 3²) = ….

3. Разложите на множители квадратный трёхчлен:

а) х² – 4х – 96; б) 2х² + 8х – 24; в) –х² + 3х + 18.

4. Сократите дробь:

а) х² + 2х – 15 б) 2х² – 5х + 2

—————; —————.

х² – 9 8х – 4

5. Найдите значение выражения

5х² – 37х + 14

——————

5х² + 3х – 2 при х = 11.

3 УРОВЕНЬ

1. Найдите корни квадратного трёхчлена:

а) х² – 4х + 3; б) 4х² – 20х + 25; в) 3х² + х + 4.

2. Выделите квадрат двучлена из квадратного трёхчлена:

а) х² – 16х + 100; б) –х² – 2х – 4; в) 2х² 8х.

3. Докажите неравенство:

а) х² + 12х + 44 > 0; б) 4х² – 12х + 9 ≥ 0.

4. Разложите на множители квадратный трёхчлен:

а) х² – 8х – 9; б) 3х² + 17х – 6; в) 2х² – 108х +1458.

5. Найдите значение выражения

2х² + 13х – 24

——————

2х² – 25х + 33 при х = 11,25.

Приложение 2.

Алгебра, 9 класс.

Фрагмент урока по теме «Разложение квадратного трёхчлена на множители».

Запишите разложение квадратного трёхчлена, зная его корни. Заполните таблицу:

х₁

х₂

квадратный трёхчлен

4

3

х² – 7х + 12 =

2

-1

5х² – 5х -10 =

0,1

-3

10х² + 29х – 3 =

9

-7

х² – 2х – 63 =

0,5

-4

2х² + 7х – 4 =

Приложение 3.

Фрагмент урока алгебры в 9 классе по теме «Квадратичная функция».

Выберите из ниже предложенных графиков те, которые являются графиками квадратичной функции:

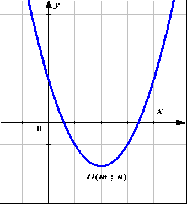
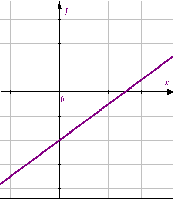
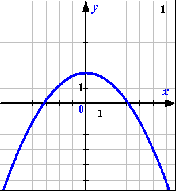
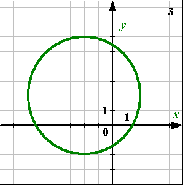
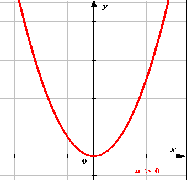
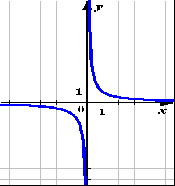
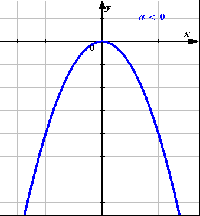
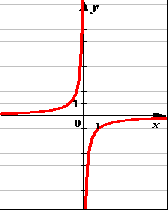
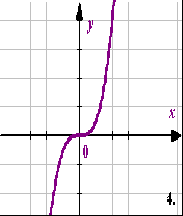
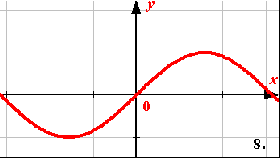
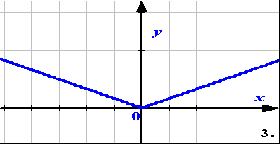
Приложение 4.

Геометрия, 8 класс.

Самостоятельная работа обучающего характера по теме «МНОГОУГОЛЬНИКИ»

1 УРОВЕНЬ.

1 ВАРИАНТ

1. Найдите сумму углов выпуклого двенадцатиугольника.

2. в выпуклом пятиугольнике две стороны равны, третья сторона на 3см больше, а четвёртая в два раза больше первой стороны, пятая – на 4см меньше четвёртой.. Найдите стороны пятиугольника, если известно, что его периметр равен 34см.

2 ВАРИАНТ

1. Найдите сумму углов выпуклого тринадцатиугольника.

2. в выпуклом шестиугольнике три стороны равны, четвёртая в два раза больше первой стороны, пятая – на 3см меньше четвёртой, а шестая – на 1смбольше второй. Найдите стороны шестиугольника, если известно, что его периметр равен 30см.

2 УРОВЕНЬ

1 ВАРИАНТ

1. Сколько сторон имеет выпуклый многоугольник, если сумма его углов равна 2160º.

2. Выпуклый четырёхугольник АВСD имеет две пары равных между собой смежных сторон:

АВ = АD, ВС = СD, О – точка пересечения диагоналей четырёхугольника. Сравните периметры пятиугольников АВСОD и АВОСD.

2 ВАРИАНТ

1. Сколько сторон имеет

выпуклый многоугольник, если сумма его углов равна 2520º.

2. Диагональ АС невыпуклого четырёхугольника АВСD разделяет этот четырёхугольник на два треугольника, причём

АВ > ВС, АВ = АD, DС = СD, а прямые, содержащие диагонали четырёхугольника, пересекаются в точке О. Сравните периметры пятиугольников ВСОDА и DСОВА.

3 УРОВЕНЬ

1 ВАРИАНТ

1. Каждый угол выпуклого многоугольника равен 162º. Найдите число сторон этого многоугольника.

2. В выпуклом шестиугольнике АВСDЕF все стороны равны. Большая диагональ, проведённая из вершины А, параллельна стороне ВС,

<ВАD = <СDА. Сравните периметры пятиугольников АВDЕF и АСDЕF.

2 ВАРИАНТ

1. Каждый угол выпуклого многоугольника равен 165º. Найдите число сторон этого многоугольника.

2. В выпуклом пятиугольнике АВСDЕ все стороны равны. Диагональ, проведённая из вершины А, параллельна стороне ЕD,

<ЕАС =

Приложение 5.

Фрагмент урока по геометрии в 8 классе по теме «Четырёхугольники».

Заполните таблицу, отметив знаки «+»(да) и «-»(нет).

парал

лелог

рамм

прямо

уголь

ник

ромб

квад

рат

1. Противолежащие стороны равны и параллельны.

2. Все стороны равны.

3. Противолежащие углы равны, сумма соседних углов равна 180°.

4. Все углы прямые.

5. Диагонали пересекаются и точкой пересечения делятся пополам.

6. Диагонали равны.

7. Диагонали взаимно перпендикулярны и являются биссектрисами углов.

Приложение 6.

Алгебра, 8 класс.

Самостоятельная работа по теме

«СВОЙСТВА ЧИСЛОВЫХ НЕРАВЕНСТВ».

1 ВАРИАНТ

1. Сравните числа а и b, если

а – b = 0,04.

2. Зная, что 5 < с < 6, оцените значения выражений:

а) с – 4;

б) – 2с.

3. Дан квадрат со стороной, равной хсм. Известно, что 2 < х < 3. Оцените

периметр этого квадрата.

2 ВАРИАНТ

1. Сравните числа а и b, если

а – b = - 0,01.

3. Зная, что 5 < с < 6, оцените значения выражений:

а) с + 3;

б) – 4с.

3. Дан равносторонний треугольник со стороной, равной у см. Известно,

что 4 < у < 5. Оцените периметр этого треугольника.

Приложение 7.

Алгебра, 8 класс.

Фрагмент урока по теме «Теорема Виета»

Заполните таблицу.

Ф.И. учащегося

—————————————————

Заполните таблицу:

Уравнение

Корни х₁, х₂

х₁ + х₂

х₁ · х₂

х² - 4х + 3 = 0

х² + 6х – 7 = 0

х² - х – 12 = 0

х² - 7х +12 = 0

х² + 8х +15 = 0

Выявите закономерность связи между корнями и коэффициентами приведённого квадратного уравнения, используя приведённую выше таблицу.

Приложение 8.

Алгебра, 9 класс.

Контрольная работа по теме «Прогрессии».

ВАРИАНТ 1

1. Последовательность (х_n) задана формулой (х_n) = 2n² - 3n. Найдите четвёртый член этой последовательности.

2. Найдите 42-й член арифметической прогрессии (а_n), первый член которой равен 84, а разность равна -3.

3. Найдите шестой член геометрической прогрессии (b_n), если b₁ = 3,5, q = -2.

4. Найдите сумму шестнадцати первых членов арифметической прогрессии (а_n): 8; 4; 0; …

5. Первый член геометрической прогрессии (b_n) равен 2, а знаменатель 3. Найдите сумму шести первых членов этой

прогрессии.

ВАРИАНТ 2

1. Найдите двадцать третий член арифметической прогрессии (а_n), если её первый член равен -15, а разность равна 3.

2. В геометрической прогрессии (b_n)

b₁ = 64, q = ½. Найдите восьмой член этой прогрессии.

3. Найдите сумму шестидесяти первых членов последовательности (х_n), заданной формулой х_n = 3n – 1.

4. Дана геометрическая прогрессия:

3; -6; … . Найдите сумму первых её шести членов.

5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.

ВАРИАНТ 3

1. Найдите сорок третий член арифметической прогрессии (а_n), если её первый член равен - 9, а разность равна 4.

2. В геометрической прогрессии (b_n)

b₁ = 27, q = - ⅓. Найдите девятый член этой прогрессии.

3. Найдите сумму сорока первых членов последовательности (у_n), заданной формулой у_n = 4n – 2.

4. Дана геометрическая прогрессия:

5; -15; … . Найдите сумму первых её шести членов.

5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.

Приложение 9.

Фрагмент урока геометрии в 8 классе по теме

«Синус, косинус и тангенс острого угла прямоугольного треугольника».

Решите самостоятельно задачу:

Докажите, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны и тангенсы этих углов равны.

Наводящие вопросы к задаче:

- Что можно сказать о треугольниках АВС и МNК?

- Что можно сказать об отношениях их сходственных сторон?

- Примените основное свойство пропорции к равенству

ВС АВ АС АВ

—— = —— ( —— = ——).

NМ КN КМ КN

- Что можно сказать об отношении противолежащего катета к гипотенузе (прилежащего катета к гипотенузе)?

- Чем можно заменить отношение

ВС NМ АС КМ

—— ( —— ; —— ; —— ) ?

АВ КN АВ КN

- Выразите tgA через sinA и cosA (tgК через sinК и cosК).

- Равны ли tgК и tgА?

Приложение 10.

Алгебра, 9 класс.

Математический диктант по теме «Прогрессии».

1. У арифметической прогрессии первый член 5(4), второй член 7(1). Найдите разность d.

2. У арифметической прогрессии первый член 4(5), второй член 1(7). Найти третий член.

3. У геометрической прогрессии первый член 10(6), второй член 5(3). Найти знаменатель q.

4. У геометрической прогрессии первый член 6(10), второй член 3(5). Найти третий член.

5. Найти десятый(восьмой) член арифметической прогрессии, если её первый член равен 1, а разность d равна 3(4).

6. Найти четвёртый(шестой) член геометрической прогрессии, если её первый член равен 1, а знаменатель q равен -2.

7. Является ли последовательность нечётных(чётных) чисел арифметической прогрессии?

8. Является ли последовательность степеней числа 2(3) геометрической прогрессией?

Приложение 11.

Геометрия, 9 класс.

Устный опрос учащихся по карточкам по теме

«Длина окружности и площадь круга».

Карточка №1.

1. Сформулируйте определение правильного многоугольника.

2. Докажите теорему об окружности, описанной около правильного многоугольника.

3. Найдите площади секторов, на которые разбивают круг два радиуса, если угол между ними равен 36º, а радиус окружности равен 4м.

Карточка №2.

1. Какая точка называется центром правильного многоугольника?

2. Докажите теорему об окружности, вписанной в правильный многоугольник.

3. Найдите длины дуг, на которые разбивают окружность два радиуса, если угол между ними равен 72º, а радиус окружности равен 6дм.

Карточка №3.

1. Объясните, какое число обозначается буквой π и чему равно его приближённое значение.

2. Выведите формулу для вычисления площади правильного многоугольника через его периметр и радиус вписанной окружности.

3. Найдите площадь правильного шестиугольника, вписанного в окружность радиуса 3см.

Карточка №4.

1. Как выражается сторона правильного треугольника через радиус описанной окружности?

2. Выведите формулу для вычисления радиуса окружности, вписанной в правильный n-угольник, через радиус окружности, описанной около него.

3. Найдите площадь кольца, ограниченного двумя окружностями с общим центром, если их радиусы равны 5 и 10м.

Приложение 10.

Алгебра. 8 класс.

Приложение 7.

ТЕСТ ПО ТЕМЕ «ПЛОЩАДЬ МНОГОУГОЛЬНИКА».

1 вариант

1. Выберите верные утверждения:

а) площадь прямоугольника равна произведению двух его сторон;

б) площадь квадрата равна квадрату его стороны;

в) площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

2. Закончите фразу: Площадь ромба равна половине произведения …

а) его сторон;

б) его стороны и высоты, проведённой к этой стороне;

в) его диагоналей.

3. По формуле S = а · h можно вычислить площадь:

а) параллелограмма;

б) треугольника;

в) прямоугольника.

4. Площадь трапеции АВСD с основаниями АВ и СD и высотой ВН вычисляется по формуле:

а) S = АВ : 2 · СD · ВН;

б) S = (АВ + ВС) : 2 · ВН;

в) S = (АВ + СD) : 2 · ВН.

5. Выберите верное утверждение.

Площадь прямоугольного треугольника равна:

а) половине произведения его стороны на какую-либо высоту;

б) половине произведения его катетов;

в) произведению его стороны на проведённую к ней высоту.

6. В треугольниках АВС и МNК <В =

АВ · ВС АВ · АС ВС · АС

а) ————; б) ————; в) ————.

МN · NК МN · МК NК · МК

7. В треугольниках МNК и DОS высоты NЕ и ОТ равны. Тогда SМNК : SРОS = …

а) МN : РО; б) МК : РS; в) NК : ОS.

2 вариант

1. Выберите верные утверждения:

а) площадь квадрата равна произведению его сторон;

б) площадь прямоугольника равна произведению его противолежащих сторон;

в) площадь прямоугольника равна произведению двух его соседних сторон.

2. Закончите фразу: Площадь параллелограмма равна произведению …

а) двух его соседних сторон;

б) его стороны на высоту, проведённую к этой стороне;

в) двух его сторон.

3. По формуле S = d1·d2 : 2 можно вычислить площадь:

а) параллелограмма;

б) треугольника;

в) ромба.

4. Площадь трапеции АВСD с основаниями ВС и АD и высотой СН вычисляется по формуле:

а) S = СН · (ВС + АD) : 2;

б) S = (АВ + ВС) · СН : 2;

в) S = (ВС + СD) · СН : 2.

5. Выберите верное утверждение.

Площадь треугольника равна:

а) половине произведения его сторон;

б) половине произведения двух его сторон;

в) произведению его стороны на какую-либо высоту.

6. В треугольниках АВС и DЕF <С =

АС · АВ АВ · АС АС · ВС

а) ————; б) ————; в) ————.

DЕ · DF DЕ · ЕF DF · ЕF

7. В треугольниках DЕF и ТRQ высоты DА и ТВ равны. Тогда SDЕF : SТRQ = …

а) ЕF : RQ; б) DЕ : ТR; в) ЕF : RТ.