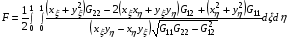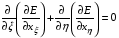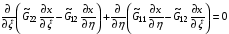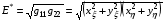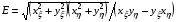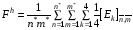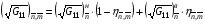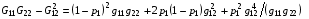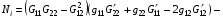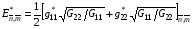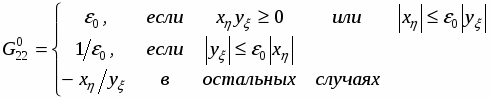Ордена Ленина

Институт прикладной математики

имени М.В. Келдыша

Российской академии наук

Г.П. Прокопов

Универсальные вариационные функционалы

для построения двумерных сеток.

Москва, 2001 год

УДК 519.63

Универсальные вариационные функционалы для построения двумерных сеток.

Прокопов Г.П.

Препринт Института прикладной математики им. М.В. Келдыша РАН

Рассматриваются функционалы, позволяющие получить произвольные невырожденные двумерные сетки при соответствующем назначении или определении в ходе расчета метрических параметров искомой сетки. Рассматриваются вопросы конструирования ортогональных или близких к ним сеток (квазиортогональных), построения дискретных моделей для расчета сеток, алгоритмов для метрических параметров и численного решения задачи минимизации функционалов.

Работа выполнена при поддержке Российского Фонда Фундаментальных Исследований (проект № 99-01-00922).

Universal variational functionals for 2D grid generation.

G.P. Prokopov

Preprint, Keldysh Institute of Applied Mathematics, RAS

Functionals that allow to obtain arbitrary invertible 2D grids at corresponding assignment or definition of grid metric parameters during the calculation are considered. The generation of orthogonal grids or close to them quasi-orthogonal grids, construction of discrete models to compute grid, algorithms for metric parameters and numerical solution of problem of functional minimization are considered.

This work was supported by Grant 99-01-00922 from the Russian Foundation for Fundamental Investigations.

Содержание

стр.

Введение…………………………………………………………………. 3

§ 1. Описание вариационных функционалов………………………….. 4

§ 2. Об ортогональных, квазиортогональных и квазиизометрических

сетках………………………………………………………………… 9

§ 3. Переход к дискретной модели……………………………………... 16

§ 4. Назначение метрических параметров……………………………… 20

§ 5. О численных алгоритмах минимизации функционалов………….. 27

§ 6. Разнообразие форм универсальных функционалов и проблема

неединственности решения………………………………………… 31

Заключение………………………………………………………………. 34

Литература……………………………………………………………….. 35

Введение.

Вариационный подход к задаче построения сеток для численного решения разнообразных задач математической физики получил весьма широкое распространение. При таком подходе задача построения сетки в простейшем случае отдельного криволинейного четырехугольника трактуется как дискретная реализация невырожденного отображения параметрической области (квадрата или прямоугольника) на область, в которой требуется построить сетку. Это отображение получается в результате минимизации некоторого вариационного функционала. Неопределенность требований, предъявляемых к сеткам (за исключением одного – невырожденности), порождает большой поток работ, посвященных этим вопросам. Некоторая часть их предлагает различные формы для минимизируемых функционалов.

Совсем недавно одну из таких работ [1] опубликовал С.А. Иваненко и ознакомил автора настоящей статьи с другой своей работой, направленной для публикации. Эта работа [2] содержит принципиальный и важный для практики результат: предложенный в [1] вариационный функционал позволяет реализовать любую невырожденную сетку при соответствующем задании входящих в него параметров, т.е. функционал носит достаточно универсальный характер.

Это, конечно, еще не решает полностью проблему построения двумерных сеток, лишь подменяя ее задачей назначения или определе-ния в ходе расчета некоторых метрических параметров искомой сетки. Однако сам факт их существования и возможностей целенаправленного поиска имеет весьма существенное значение для практики.

Предложенный в [1] функционал почти совпадает с опубликованным еще в 1967 г. в совместной работе [3] С.К. Годунова и автора настоящей статьи. «Почти» означает присутствие в знаменателе функционала [1] дополнительного сомножителя – якобиана искомого отображения. Авторами [3] он был опущен сознательно, чтобы упростить вариационные уравнения Эйлера-Лагранжа для расчета искомой сетки.

Сравнение этих двух функционалов обнаруживает между ними теснейшую связь. Оказывается, функционал из работы [3] имеет столь же универсальный характер. Обсуждение различных связанных с этим вопросов, в первую очередь – о назначении или определении метрических параметров искомой сетки, составляет содержание настоящей работы.

§ 1. Описание вариационных функционалов.

В работе [1] для создания алгоритмов построения двумерных разностных сеток предложено использовать вариационный функционал следующего вида:

1. 

Здесь {G_lm, l,m=1,2} – элементы симметричной, положительно определенной матрицы G(ξ,η), заданной в каждой точке единичного квадрата Q:{0≤ξ≤1, 0≤η≤1}. Функционал минимизируется на классе функций x(ξ,η), y(ξ,η), являющихся гладким продолжением внутрь квадрата Q заданных на его границе функций (х_Г,у_Г). Они осуществляют гладкое взаимно однозначное отображение границы квадрата Q на границу области Ω, в которой должна быть построена сетка.

Введем в рассмотрение симметричную и положительно определенную матрицу 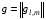с элементами

(1.2) , , .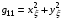

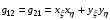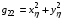Подынтегральное выражение в (1.1) называется плотностью энергии отображения

3. .

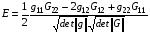Следуя автору [1], его можно записать в виде

3. ,

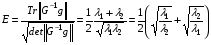где Tr означает сумму диагональных элементов матрицы,

λ₁ и λ₂ – собственные числа матрицы G^-1g.

Из (1.4) следует, что Е≥1. Равенство Е=1 достигается тогда и только тогда, когда λ₁ = λ₂ . Это можно было бы доказать и непосредственной выкладкой, что и будет сделано несколько позже (см. формулы (2.1)-(2.3)).

Отметим некоторые свойства рассматриваемого функционала.

1.1. Пусть x(ξ,η), y(ξ,η) – произвольное гладкое невырожденное отображение параметрического квадрата Q на область . Положим

(1.5) , ,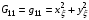

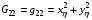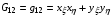
и используем очевидное тождество:

(1.6) .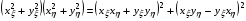

Тогда обнаруживаем, что для отображения с такими метрическими параметрами Е1, F=1, т.е. получаем абсолютное минимальное значение функционала (1.1).

Следовательно, произвольное гладкое невырожденное отображение может быть реализовано как решение задачи минимизации функционала (1.1) с некоторой конкретной матрицей G(ξ,η). Этот факт отмечается в работе [2]. Функционал (1.1) можно рассматривать как универсальный генератор произвольных невырожденных отображений квадрата Q на область ..

Заметим, что элементы матрицы G определены не однозначно. Если таковой является матрица G с элементами G_l,m, то годится и любая матрица с элементами (ξ,η)G_l,m, где (ξ,η) – произвольная достаточно гладкая функция на квадрате Q. Такой произвол устраняется нормировкой: вместо матрицы G удобно ввести матрицу 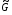с элементами

(1.7) ;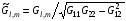

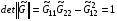
Ее элементы определяются двумя гладкими функциями f₁(ξ,η) и f₂(ξ,η), которые удовлетворяют условиям:

(1.8) 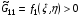, , 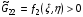, 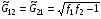f₁f₂1.

В частности, если полагать

(1.9) , ,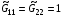

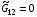то реализуются отображения, которые обычно называют гармоническими, как и соответствующие им сетки.

Более существенная причина неоднозначности матриц G: например, для гармонического отображения матрица, определяемая формулами (1.5), совсем не обязана давать результат (1.9), хотя и реализуется одно и то же отображение.

1.2. Рассмотрим теперь вариационный функционал

10. ,

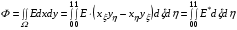где

10. .

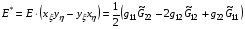Такой функционал, отличающийся от (1.1) отсутствием якобиана искомого отображения в знаменателе подынтегрального выражения, был предложен в работе [3], а затем приведен на стр. 230 монографии [4]. В определенном смысле решение не включать якобиан отображения, избрав для подынтегрального выражения функционала формулу (1.11), было принято сознательно. Авторов [3] беспокоила проблема решения возникающих эллиптических уравнений Эйлера-Лагранжа. Об этом написал С.К. Годунов на стр. 21 своих воспоминаний [5] о создании метода решения газодинамических задач, который получил широкое распространение и теперь его обычно называют методом Годунова. Основания для упомянутого беспокойства есть и в настоящее время.

Согласно теории вариационного исчисления для функционалов с подынтегральной частью 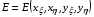, зависящей только от первых производных искомых функций, уравнения Эйлера-Лагранжа имеют вид:

10. 

.

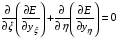Поэтому для функционала (1.10)-(1.11) эти уравнения будут следующими:

10. 

,

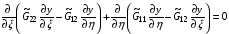если элементы 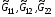матрицы G, нормированные согласно (1.7), являются функциями независимых переменных ξ,η.

Для функционала (1.1) уравнения (1.12) будут иметь гораздо более сложный вид. Это очевидно хотя бы из сравнения соответствующих уравнений для гораздо более простого случая гармонических отображений (1.9). Пока нам нет необходимости выписывать уравнения (1.12) для функционала (1.1), это будет сделано позже в § 5.

1.3. Между функционалами (1.1) и (1.10)-(1.11) существует теснейшая связь. Рассмотрим случай, когда в результате минимизации функционала (1.1) достигается его абсолютный минимум F=1. Примером такой ситуации является рассмотренная в разделе 1.1. с назначением величин G₁₁, G₂₂, G₁₂ формулами (1.5). Очевидно, что в таких ситуациях минимизация функционала (1.10)-(1.11) достигается на том же (важно!) невырожденном отображении и абсолютный минимум функционала (1.10)-(1.11)

10. ,

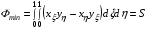где S – площадь области . Между тем получение искомого решения с помощью (1.10)-(1.11) несомненно проще и экономнее, чем с помощью (1.1).

Ситуация существенно изменяется в случае, если в процессе минимизации абсолютный минимум функционала не достигается. Тогда минимумы функционалов (1.1) и (1.10)-(1.11) реализуются, как правило, на разных отображениях. Несомненным преимуществом функционала (1.1) является то, что он гарантирует получение невырожденного отображения (другие просто не рассматриваются в качестве допустимых функций при его реализации). Подчеркнем, что это последнее замечание является предметом специальной заботы при численной реализации алгоритма минимизации функционала (1.1).

Недостаток функционала (1.10)-(1.11) – то, что его минимизация может приводить к получению отображения вырожденного (с якобианом, обращающимся в нуль в некоторых точках квадрата Q).

1.4. Подтверждением последнего утверждения является пример отображения, построенный автором и впервые опубликованный в [7]. Для дальнейшего полезно его кратко изложить.

Рассмотрим отображение, описываемое формулами:

(1.15) ,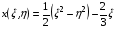

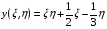
на квадрате Q:{0≤ξ≤1, 0≤η≤1}. Очевидно, что оно удовлетворяет уравнениям Лапласа:

(1.16) , ,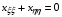

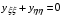и, следовательно, минимизирует интеграл Дирихле, который получается при назначении в (1.11) 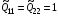, 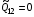. Легко видеть, что уравне-ния (1.13) тогда превращаются в (1.16). Якобиан отображения (1.15)

(1.17)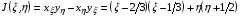

Поскольку 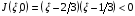на участке =0, 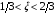, отображение образует складку в окрестности образа нижней границы квадрата Q. Пример (1.15) интересен тем, что форма области , ограничиваемой образом контура квадрата Q, имеет очень простой вид.

Ввиду важности этого примера в методическом плане заметим еще следующее. Наибольшая глубина проникновения области складки в квадрат Q получается при =1/2 и достигает координаты 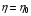, определяемой условием 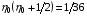. Из него получается 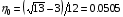. Следовательно, отображение (1.15) невырождено на прямоугольнике («урезанном квадрате») Q₀: (01, ₀<1), а складка занимает часть «полоски» 0₀. Можно поступить иначе: если в (1.15) заменить  на (-₀)/(1-₀), то получится отображение, которое будет невырождено на всем параметрическом квадрате Q, но будет вырождаться (образуя складку) на прямоугольнике 01, -₀/(1-₀)1.

Отмеченный выше недостаток функционала (1.10)-(1.11), что в процессе минимизации он может приводить к вырожденному отображению, может превращаться в его большое преимущество. Для практики расчета сеток очень трудной является ситуация, когда не удается имеющимися в распоряжении исполнителя средствами получить невырожденное начальное приближение для сетки (например, в силу сложной формы границ области уже в исходный момент расчета). Способность функционала (1.10)-(1.11) работать с вырожденными отображениями становится его очевидным достоинством в случае, если в итоге минимизации получится отображение невырожденное (возможность таких ситуаций очевидна). Тогда это путь преодоления описанных трудностей, причем средствами, имеющимися в распоряжении исполнителя. Следует однако иметь в виду, что возможно и обратное, т.е. описанный прием не является надежным и может не давать положительного результата даже в относительно простых ситуациях, о чем и свидетельствует приведенный пример (1.15).

1.5. Уместно отметить также относительно недавнее появление работы [6], в которой рассматривался вариационный функционал вида:

(1.18) ,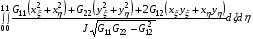

похожий на (1.1), но отличающийся от него. Для этого функционала утверждается, что «решение задачи построения допустимого приближения может быть резко упрощено, если заменить исходный функционал на регуляризованный, дискретный аналог которого был бы близок дискретному аналогу исходного функционала в допустимой области, являлся бы бесконечно дифференцируемой функцией от своих аргументов и стремился бы к + по мере удаления от допустимого множества». Согласно работе [6], эта цель достигается, если в знаменателе функционала заменить якобиан J искомого отображения на величину

19. ,

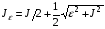где  - некоторый малый параметр (<<1).

Однако и минимизация регуляризованного функционала сталкивается с серьезными трудностями, связанными с неединственностью решения. Вопрос о неединственности будет предметом обсуждения в § 6.

§ 2. Об ортогональных, квазиортогональных и квазиизометрических сетках.

2.1. Предлагая, как уже упоминалось, в [3] и затем в [4], вариационный функционал (1.10)-(1.11), авторы сопровождали его тождеством, в котором легко убедиться непосредственной проверкой:

1. ,

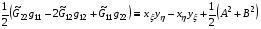где

(2.2) ,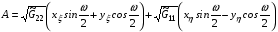

,

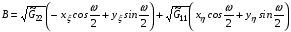а величина  (0<<) определяется формулой:

(2.3)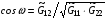

Из (2.1) очевидно следует, что для Е, определенной формулой (1.3), выполнено неравенство Е1.

Рассмотрим случай, когда в процессе минимизации достигается абсолютный минимум функционала (1.10)-(1.11), равный площади S области . Тогда искомые функции x(ξ,η), y(ξ,η), его реализующие, удовлетворяют уравнениям А=0, В=0. Последние могут быть записаны так:

(2.4)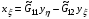

.

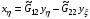Они известны в теории квазиконформных отображений как уравнения Бельтрами.

Обратимся еще раз к примеру отображения (1.15). Поскольку оно получено при 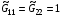, , 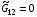уравнения (2.4) приобретают вид:

(2.5) , ,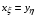

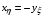что соответствует классическому конформному отображению. Очевидно, что (1.15) таковым не является (заметим, что оно так и задумывалось в работе [7]):

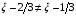, +1/2.

Следовательно, приведенный пример иллюстрирует ситуацию, когда абсолютная минимизация функционала не достигается.

Любопытно отметить следующее обстоятельство. Если для отображения (1.15) кропотливо вычислить величины G₁₁, G₂₂, G₁₂ по формулам (1.5) и проверить уравнения (2.4) с этими метрическими параметрами, то оказывается, что уравнения (2.4) будут выполнены! Причем не только на прямоугольнике Q₀, упомянутом в разделе 1.4., где отображение (1.15) невырождено, а и на полном параметрическом квадрате Q, но с одной существенной оговоркой: в качестве величины 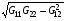при нормировке (1.7) берется 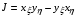, вычислен-ная по формуле (1.17). Между тем должно быть 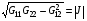. Если бы отображение (1.15) было невырожденным, это не имело бы значения, так как 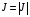. Однако это не так из-за упомянутой складки отображения. Причина невыполнения уравнений (2.5) в случае 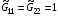, 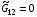будет обсуждаться ниже в разделе 2.5.

2.2. Особый интерес для практики расчетов представляют сетки, порождаемые ортогональными отображениями, удовлетворяющими условию:

6. .

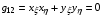Предполагая, что такое отображение существует и невырождено, подставим выражения (2.4), которым оно должно удовлетворять, в условие (2.6). После несложных выкладок будем иметь:

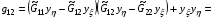
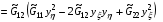
Поскольку матрица 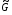является положительно определенной, 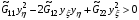, за исключением тривиального случая .

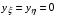Следовательно, для выполнения условия g₁₂=0 необходимо, чтобы .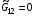

Таким образом, минимизация функционалов (1.1) или (1.10)-(1.11) дает ортогональную сетку только в случае, если .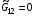

Необходимое условие 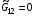однако не является достаточным. Об этом свидетельствует хотя бы рассмотренный пример отображения (1.15).

2.3. При 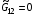уравнения (2.4) приобретают вид:

(2.7) , .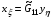

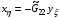Отсюда получаются формулы для назначения величин 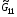и :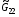

(2.8) , .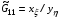

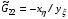Чтобы преодолеть противоречия или даже аварийные ситуации (например, если окажется, что предполагаемое ортогональное отображение не существует), а также обеспечить выполнение условий (1.8), будем реализовать формулы (2.8) в модифицированном виде:

(2.9)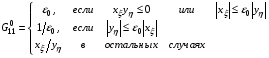

Здесь ₀ – некоторый управляющий параметр, задающий уровень «срезания» величин 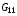, 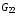. Нормировка (1.7), если делается, то после (2.9).

2.4. В случае назначения 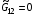вид функционалов (1.1) и (1.10)-(1.11), естественно, упрощается. Формулы для плотности энергии отображения (1.11) и (1.3) приобретают вид (нормировка (1.7) не обязательна):

(2.10)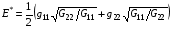

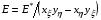
В свою очередь, если метрические параметры назначаются формулами (1.5), формулы (2.10) приобретают вид:

11. 

12. 

Попытка использовать для построения сеток вариационный функционал с подынтегральным выражением (2.11) предпринималась автором еще в работе [9] и представлена на стр.234-235 монографии [4]. Вопросы применения для построения сеток формул (2.11)-(2.12) и их обобщений обсуждались в [8]. Обобщение формул (2.11)-(2.12) состояло в использовании в качестве величины Е степеней полученных выражений. Это делалось в интересах практики расчетов с целью обеспечения большего разнообразия конструируемых сеток.

В связи с этим заслуживает быть отмеченным следующее обстоятельство. Назначим в функционале (1.1) метрические параметры формулами:

(2.13) , ,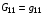

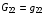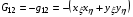
Тогда для плотности энергии отображения Е с учетом тождества (1.6) получим:

.

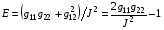Поскольку слагаемое –1 при минимизации не играет роли, также как и сомножитель 2, получаем для Е формулу:

(2.14) ,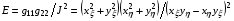

которая представляет квадрат выписанной в (2.12). Функционал такого вида исследовался в работе [10] и было установлено, что возникающая при этом задача является некорректной. Это подтверждается и числен-ными экспериментами. Поэтому функционал с (2.14) для построения сеток использовался не в «чистом» виде, а в комбинации с функциона-лами другого целевого назначения. В упомянутой работе [8] был избран другой путь преодоления некорректного характера задачи, условно названный автором регуляризацией функционалов. Некоторые результа-ты численных экспериментов по его реализации представлены в [11].

2.5. Осторожные оговорки о предполагаемом существовании ортогонального отображения имеют под собой глубокие основания. Фактически при дискретной реализации, изложение которой будет сделано в следующем параграфе, можно рассчитывать в лучшем случае на получение сетки, лишь в некотором смысле близкой к ортогональной. Будем называть ее квазиортогональной.

Причин для этого несколько. Прежде всего отметим, что при дискретной реализации восполнение линий сетки обычно осуществляется отрезками прямых, соединяющих соседние узлы сетки, т.е. ломаными линиями. Поэтому, строго говоря, ортогональными являются только сетки, составленные из прямоугольных ячеек. Это – причина аппроксимационного характера, ослабевающая при увеличении числа интервалов сетки, выстраиваемой в области с зафиксированными границами.

Вторая причина – недоведение до сходимости итерационных процессов при реализации алгоритмов. Это дорого и нецелесообразно, поскольку вполне приемлемой для расчета может оказаться сетка, получаемая уже на ранней стадии расчета.

Наконец, наиболее глубокая математическая причина состоит в следующем. Как уже отмечалось, при решении задачи может не достигаться абсолютный минимум функционала. Это может случиться, например, по причине «застревания» итерационного процесса в некоторой локальной экстремальной точке.

Однако есть и более серьезная причина, обусловленная математической постановкой задачи. Как уже отмечалось для примера (1.15), при достижении абсолютного минимума вариационного функционала для решения должны быть выполнены уравнения (2.5) классического конформного отображения. Однако они не выполняются. Почему? Согласно известной теореме Римана при конформном отображении можно задавать соответствие только трех точек на контуре физической области и параметрического прообраза. Между тем заданием граничных условий задачи фиксируется определенное соответствие всех точек на контуре. Тем самым множество допустимых функций при минимизации функционала оказывается настолько узким, что не содержит решения задачи о конформном отображении. Между тем именно оно обеспечило бы абсолютную минимизацию функционала.

Можно было бы изменить постановку задачи, разрешив движение точкам на контуре физической области . Отказ (в производственных интересах) от такой возможности автоматически влечет за собой отказ от ортогональной сетки (в дифференциальной постановке) в пользу «квазиортогональной». Исключение могут составить лишь благоприят-ные ситуации задания удачного соответствия граничных точек.

Изменение постановки задачи с движением точек на контуре физической области  может стать предметом специального обсуждения. Некоторый вариант ее реализации рассматривался на стр.20-23 работы [11].

2.6. Как следует из изложенного выше, существует определенная принципиальная разница в ситуациях, когда в процессе минимизации вариационного функционала достигается его абсолютный минимум или этот минимум не достигается.

В дополнение, несколько опережая избранный порядок изложения, заметим, что в работе [2] для дискретного варианта функционала (1.1) доказано существование единственного решения в случае, если метрические параметры G₁₁, G₂₂, G₁₂ обеспечивают его абсолютный минимум. Вопрос о единственности решения в случае, когда абсолютный минимум не достигается, остается открытым и, более того, подвергается серьезным сомнениям (см. ниже § 6).

Стремление выделить специальный класс квазиконформных отображений, для которого можно обосновать существование и единственность искомого отображения, для функционала вида (1.10)-(1.11) было реализовано в работе [12]. Описание численной реализации соответствующего алгоритма было опубликовано на стр. 237-241 монографии [4].

Продолжение этого направления исследований нашло отражение в ряде работ, в частности, в [13-14]. В них рассматриваются так называемые квазиизометрические отображения.

Отображение x(ξ,η), y(ξ,η) называется квазиизометрическим, если отношение расстояния между любыми (достаточно близкими) точками к расстоянию между их образами ограничено сверху и снизу:

.

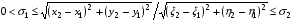Отображение x(ξ,η), y(ξ,η) единичного квадрата Q на область  называется 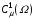-отображением, если частные производные 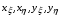непрерывны и удовлетворяют условию Гельдера с показателем .

Пусть четыре границы криволинейного четырехугольника  достаточно гладкие – удовлетворяют условию Гельдера с показателем . Обозначим 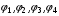величины углов, которые образуют пары соседних границ в вершинах . Главный результат работы [13] состоит в следующем.

Если выполнены условия:

, , ,

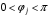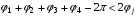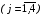то любое квазиизометрическое 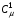-отображение границ продолжается до квазиизометрического 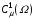-отображения квадрата Q на область .

При этом метрика отображения выбирается из пятипараметрического семейства метрик специального вида, заданных в единичном квадрате. Они представляют общий вид метрик, в которых геодезическими являются прямые линии. В [13] доказано, что существует единственная метрика такого вида, в которой единичный квадрат К отображается в  конформно и квазиизометрически.

В работе [14] представлен алгоритм построения квазиизометрических сеток, основанный на этом результате. При его кратком описании придется в интересах сохранения наших обозначений, цитируя [14], поменять роли (u,v) и (x,y) и вместо аргументов (s,t) использовать обозначения (,). Искомое квазиизометрическое отображение х(,), у(,) конструируется как суперпозиция двух отображений: x=x(u,v), y=y(u,v) отображает единичный квадрат K:{0u, v1} на ; u=u(,), v=v(,) отображает квадрат Q на K.

Второе отображение можно представить геометрически как переход от равномерной сетки на Q к сетке на K, образованной прямолинейными отрезками. Они соединяют образы соответствующих граничных точек квадрата Q, находящихся на противоположных сторонах K. Отображение нижней и верхней сторон определяется функциями 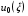, , 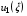а левой и правой - функциями 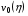, 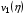. Естественно, предполагаются выполненными условия согласования:

, .

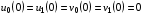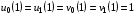Отображение x(u,v), y(u,v) квадрата K на область  минимизирует функционал вида (1.10)-(1.11), для которого метрика выбирается из упомянутого выше пятипараметрического семейства с параметрами S₁ , S₂ , S₃ , S₄ , k. Последний из них k представляет конформный модуль криволинейного четырехугольника  - отношение сторон прямоугольника, на который он может быть конформно отображен.

Искомые функции х(,), у(,), отображающие Q на , получаются из условия минимума функционала, также имеющего вид (1.10)-(1.11), который минимизируется по трем группам переменных:

1^о параметрам S₁ , S₂ , S₃ , S₄ , k ;

2^о управляющим граничным функциям , , , ;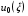

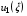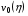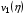3^о функциям х(,), у(,).

Вычислительный алгоритм, реализующий указанные отображения, достаточно сложен, и его описание выходит за рамки настоящей работы.

§ 3. Переход к дискретной модели.

3.1. Следующим этапом работы по созданию алгоритмов расчета сеток является переход от дифференциальной формы вариационного функционала к дискретной. Мнение о том, что этот этап сводится к механической замене дифференциальных выражений разностными, является ошибочным. При такой замене могут быть утеряны важные свойства дифференциальной модели. Рассматриваемая задача может служить иллюстрацией такой ситуации.

Для того, чтобы правильно передать обращение в нуль якобиана отображения при разностной аппроксимации функционала (1.1), может быть использована специальная процедура, известная под названием вариационного барьерного метода. Она была разработана для расчета гармонических сеток, хорошо известна и многократно описана. Поэтому не будем на ней останавливаться. Изложим окончательный результат, представленный в работе [2], имеющий непосредственное отношение к функционалу (1.1), с некоторыми (более привычными для нас) изменениями (в основном – в обозначениях).

Рассматривается задача построения двумерной регулярной сетки

(3.1) , ,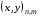

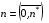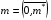
при заданных координатах граничных узлов

, , ,

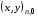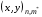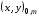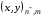
на контуре, ограничивающем односвязную область  на плоскости (х,у).

Пусть координаты (х,у)_n,m узлов сетки заданы (можно говорить о них, как о некотором исходном приближении для искомой сетки). Рассмотрим ячейку сетки и занумеруем вершины, обходя ее контур против часовой стрелки: узлу (n,m) присвоим номер k=1, узлу (n+1,m) - номер k=2, узлу (n+1,m+1) - k=3, узлу (n,m+1) - номер k=4. В последующих выражениях следует полагать k-1=4 при k=1 и k+1=1 при k=4.

Ячейке с такими вершинами обычно присваивают громоздкий «полуцелый» номер (n+1/2,m+1/2). Вместо этого условимся о присвоении ей менее громоздкого номера 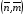, отмечая верхней чертой условное прибавление +1/2. Соответственно 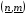заменит номер

(n-1/2,m-1/2) , 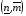- номер (n-1/2,m+1/2), наконец 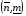- номер (n+1/2,m-1/2).

Дискретный аналог функционала (1.1) записывается тогда в виде:

2. 

,

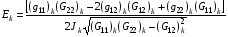где

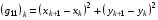
(3.3)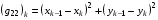

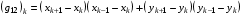
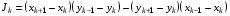
Будем предполагать, что все J_k>0 для всех ячеек сетки, т.е. все ячейки сетки – выпуклые четырехугольники. Такую сетку будем называть выпуклой (автор [2] называет ее невырожденной).

(G₁₁, G₁₂, G₂₂)_k - элементы симметричных положительно определенных матриц G_k, отнесенных к треугольнику с номером k в ячейке с номером .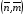

Непосредственной проверкой можно убедиться в тождественном выполнении соотношения

(3.4) ,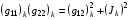

которое является разностным аналогом тождества (1.6). Если, в соответствии с (1.5), назначить элементы матриц G_k формулами:

(3.5) , , ,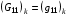

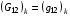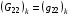то оказывается, что 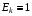для всех k и всех ячеек сетки , .

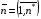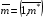Следовательно, для заданной сетки (3.1) получаем по формулам (3.2) значение F^h=1, т.е. абсолютный минимум этой суммы, представляющей дискретный аналог функционала (1.1). Таким образом, задание элементов матриц G формулами (3.5) реализует заданную произвольным образом выпуклую (невырожденную) сетку (3.1) как решение задачи минимизации дискретного функционала F^h.

В работе [2] доказано, что сетка принадлежит к классу выпуклых (невырожденных) сеток тогда и только тогда, когда она минимизирует функционал (3.2) для некоторого набора положительно определенных и симметричных матриц G_k.

3.2. Аналогичный дискретный функционал можно было бы построить и для (1.10):

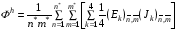
Но мы поступим иначе. Заменим в нем внутреннюю сумму для четырех треугольников одной ячейки одним слагаемым следующего вида:

(3.6)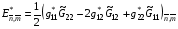

Величины в правой части (3.6) будем вычислять без разбиения ячейки на треугольники по формулам, которые для краткости используют описанную выше нумерацию вершин ячейки:

,

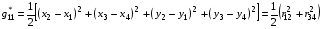(3.7)

,

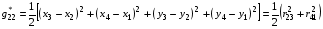где .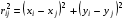

Для площади ячейки J^* и площадей треугольников _k =J_k /2 имеем:

.

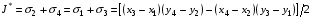Пусть _k – угол в вершине ячейки с номером k. Тогда

.

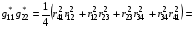
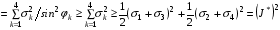Чтобы обеспечить выполнение тождества, аналогичного (3.4), определим величину 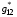формулой:

(3.8)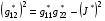

Заметим, что формула (3.8) определяет величину 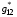только с точностью до знака. Однако этого будет достаточно при тех вариантах назначения G₁₂ , которые рассматриваются ниже в § 4.

Аппроксимируем функционал (1.10)-(1.11) суммой

(3.9)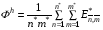

Если назначить величины

(3.10) , ,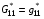

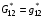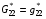
и нормировать их:

(3.11) , , ,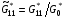

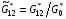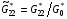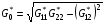
то точно так же, как и ранее, оказывается, что 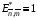для всех ячеек сетки.

Будем предполагать, что для заданной произвольной сетки все ячейки удовлетворяют требованию 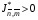. Заметим, что это требование более слабое, чем выпуклость всех ячеек, поскольку допускает присутствие невыпуклых ячеек, но при условии отсутствия ячеек самопересекающихся (у них пересекается одна из двух пар противоположных границ). Будем называть такую сетку несамопересекающейся.

Полученный результат можно сформулировать так. Произвольно заданная несамопересекающаяся сетка (3.1) реализуется как решение задачи о минимизации дискретного функционала, описываемого формулами (3.6)-(3.9), если задать элементы матриц G^* формулами (3.10)-(3.11).

Далее отметим, что поставленной цели тождественной передачи дифференциального соотношения (1.6) в разностной форме (3.4) легко было бы добиться и другим способом. Достаточно было бы назначить:

,

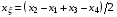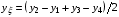
(3.12) ,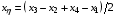

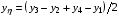
и далее вычислять g₁₁, g₂₂, g₁₂ по их дифференциальным выражениям (1.2).

Предпочтение формулам (3.7)-(3.8) носит содержательный характер, поскольку обеспечивает получение лучшей формы для системы разностных уравнений, которые будут рассматриваться позднее в § 5.

3.3. Сделаем несколько замечаний о дискретизации задачи.

Во-первых, очевидно, что решение такой задачи для функционала (3.6)-(3.9) менее громоздко, чем для функционала (3.2)-(3.3). Во всяком случае при фиксированных матрицах G минимизация функционала (3.9), представляющего квадратичную форму от искомых координат узлов сетки, сводится к решению системы линейных алгебраических уравнений. В случае же функционала (3.2)-(3.3) даже при фиксированных матрицах G решать придется систему нелинейных уравнений из-за присутствия в знаменателе (3.2) величин J_k , моделирующих якобиан искомого отображения.

Во-вторых, минимизация функционала (3.2)-(3.3) осуществляется на множестве выпуклых сеток. Существование «выпуклого» решения при произвольном наборе фиксированных положительно определенных и симметричных матриц G_k доказано в [2]. Это доказательство использует наличие бесконечного барьера на границе класса выпуклых (невырожденных) сеток.

В отличие от этого минимизация функционала (3.6)-(3.9) осуществляется на множестве несамопересекающихся сеток. Естественно было бы ожидать, что искомое решение также будет несамопересекающейся сеткой. Однако наличие примера (1.15) обнаруживает, что это не всегда так. Как уже обсуждалось в разделе 1.3., это является, с одной стороны, недостатком, а с другой стороны – преимуществом дискретного функционала (3.6)-(3.9) перед дискретным функционалом (3.2)-(3.3).

Обратим внимание, что в знаменателе функционала (1.10)-(1.11) исчез якобиан искомого отображения, однако сохранился сомножитель 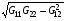. Он присутствует в знаменателе формул (3.6). Это позволяет в ходе расчета не с фиксированными, а переменными матрицами G, позаботиться о создании для функционала (3.6)-(3.9) бесконечного барьера, аналогичного упомянутому выше для функционала (3.2)-(3.3). Требуется соответствующее назначение матриц G (этот вопрос будет обсуждаться в § 4) и организация итерационного процесса, при которой ячейки сохраняют несамопересекаемость. Тогда можно гарантировать, что минимум функционала (3.6)-(3.9) будет достигаться на сетке, которая не содержит самопересекающихся ячеек.

§ 4. Назначение метрических параметров.

4.1. Универсальный характер функционалов (1.1) и (1.10)-(1.11), позволяющий после их дискретизации и решения соответствующей задачи минимизации в принципе получить любую невырожденную сетку, еще не исчерпывает проблемы построения двумерных сеток до тех пор, пока не даны конкретные рекомендации по назначению метрических параметров G₁₁, G₁₂, G₂₂ . Формулы (1.5) позволяют лишь воспроизвести имеющуюся сетку, но никак не конструировать новую.

Для назначения метрических параметров G₁₁, G₁₂, G₂₂ просматриваются два возможных пути. Первый состоит в том, чтобы по информации о расчетной области , состоящей в задании положения узлов на ее граничном контуре, «сочинить» функции G₁₁, G₁₂, G₂₂ от параметрических координат (,), позволяющие надеяться на получение приемлемой для исполнителя сетки при минимизации рассматриваемых функционалов.

Второй путь состоит в том, чтобы в должном направлении изменять локальные параметры G₁₁, G₁₂, G₂₂ в ходе итерационного процесса, который неизбежно придется применить для осуществления минимизации функционала.

4.2. Начнем с первого пути. Пусть имеются четыре последовательности координат

(4.1) , , ,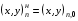

, , ,

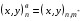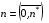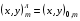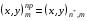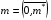задающие соответственно нижнюю, верхнюю, левую и правую границы области . Они устанавливают соответствие (взаимно однозначное) с равномерно расставленными узлами на участках границы параметрического квадрата Q:

нижним (01, =0), верхним (01, =1),

левым (01, =0) и правым (01, =1).

С равным успехом можно было бы заменить квадрат Q прямоугольником номеров расчетных точек : 0nn^*, 0mm^* .

На стр. 181 монографии [4] описана процедура расчета вспомогательной последовательности 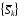, приближенно передающей расстановку узлов по длине дуги для граничной последовательности :

, ,

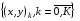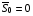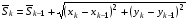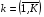
и ее последующей нормировки , .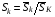

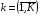Обозначим 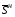, ,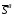, 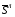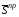суммарные вычисленные значения 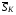для каждой из четырех границ. Назначим значения 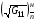, 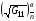для нижней и верхней границ формулами:

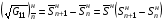
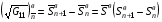
и значения 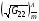, 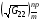для левой и правой границ аналогичными формулами:

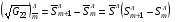
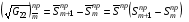
(Смысл написания индексов 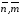был описан в разделе 3.1).

Далее величины 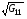, 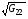внутри квадрата вычисляются по интерполяционным формулам:

2. 

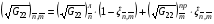
В этих формулах

(4.3)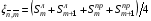

.

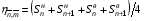Описанные формулы представляют один из возможных разнообразных вариантов интерполяционных формул. Он выбран в результате исследований [14] и при желании может быть заменен на другой. Определенных таким образом величин 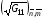и 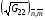достаточно для реализации формул (2.10), ориентированных на получение «квазиортогональных» сеток, поскольку при этом предполагается, что G₁₂=0.

По-видимому, целесообразно этим и ограничиться. Дело в том, что для определения величин G₁₂ в исходной информации об области  содержится возможность определения ее только в четырех угловых точках. В них смыкаются пары соседних границ.

Вычислим эти значения

, , ,

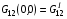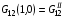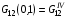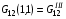
Расчетные формулы для них типа (3.3) или (3.8) опускаем ввиду их очевидности. По этим значениям можно было бы выписать интерполяционные формулы для всего квадрата Q. Естественно, что интерполировать следует не величину G₁₂, а 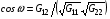или величину . В противном случае трудно гарантировать выполнение условия положительной определенности матриц 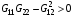для вычисленных выше величин, полученных независимой интерполяцией. При интерполяции целесообразно использовать те же значения координат 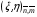, представленные формулами (4.3). Соответствующие расчетные формулы для 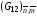приводить не будем.

Отметим, что в качестве еще одного примера реализации первого пути может рассматриваться содержащееся в работе [1] на стр. 1673-74 предложение задавать целевые формы ячеек, переходя от приграничных к ячейкам внутри области. Вполне возможно, что это предложение может быть доведено до автоматизированных алгоритмов, приемлемых для практики расчетов нестационарных задач.

4.3. Обратимся теперь ко второму пути назначения метрических параметров G₁₁, G₁₂, G₂₂.

Очевидно, что для реализации алгоритма минимизации функционала придется прибегнуть к итерационному процессу. Исходной для очередной итерации является сетка, полученная на предыдущей, для первой итерации она получается, например, с помощью интерполяционных формул. Как уже отмечалось в разделе 1.4, получение начального приближения для сетки иногда может оказаться трудной задачей. Такая ситуация и способы ее преодоления обсуждались, в частности, в работе [16].

Как отмечается в уже упоминавшейся работе [6], при реализации барьерного вариационного метода основной проблемой оказывается «прохождение» барьера снаружи в случае, когда начальное приближение не принадлежит допустимому множеству.

Поэтому, например, с точки зрения решения нестационарных задач, представляется целесообразным отделить в качестве «наиболее нелинейной» части задачу попадания внутрь допустимого множества сеток на начальном шаге. А в дальнейшем естественно предполагать, что исходная сетка удовлетворяет нужным требованиям, а именно, состоит из выпуклых ячеек, если минимизируется функционал (3.2), или не содержит самопересекающихся ячеек, если минимизируется функционал (3.6)-(3.9). Результат новой итерации также должен удовлетворять этим требованиям. Этого можно достигать посредством назначения достаточно малого коэффициента «запаса» для сдвига узла сетки на итерации, который является одним из задаваемых управляющих параметров.

Заметим, что в случае функционала (3.6)-(3.9) это позволяет предотвратить появление самопересекающихся ячеек, хотя и не может препятствовать возможному ухудшению формы отдельных ячеек, вплоть до превращения их в треугольники вместо четырехугольной формы. Назревание такой ситуации может быть воспринято как «сигнал бедствия», требующий, например, изменения управляющих параметров или переход на алгоритм расчета более надежный, например, минимизацию функционала (3.2) вместо (3.6)-(3.9).

Стоит отметить, что наличие величин 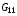и 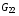в знаменателе формул (2.10) может сыграть роль бесконечного барьера и предотвратить рассматриваемую ситуацию вырождения ячейки сетки аналогично тому, как это достигается для функционала (3.2) благодаря присутствию в знаменателе якобиана.

В случае, если используется алгоритм, ориентированный на «квазиортогональные» сетки, вопрос о назначении метрических параметров G₁₁, G₁₂, G₂₂ может решаться, например, с помощью дискретизации формул (2.9) для G₁₁, G₂₂ и назначения G₁₂=0.

Чтобы «смягчить» приспосабливание алгоритма к ситуации, когда предполагаемое ортогональное отображение не существует или формулы (2.9) дают «плохой» результат по имеющемуся приближению для искомой сетки, целесообразно вместо (2.9) предусмотреть более общие формулы

,

,

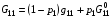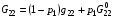где p₁ – управляющий параметр, 0<p₁1,

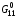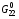, - значения, вычисленные по формулам (2.9).

В силу, как уже отмечалось, неопределенности требований, предъявляемых к сетке (кроме очевидного - невырожденности), конечно же, возможны и другие алгоритмы назначения параметров G₁₁, G₁₂, G₂₂ .

4.4. Опишем один из таких возможных алгоритмов. По имеющейся на данный момент расчета сетке (х,у)_n,m вычисляются ее метрические параметры: 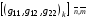по формулам (3.3) для функционала (3.2) или 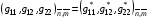по формулам (3.7)-(3.8) для функционала (3.9).

Пусть p₁, p₂ - задаваемые управляющие параметры, подчиненные условиям:

(4.4) 0p₁1, 0p₂1

Назначим метрические параметры G₁₁, G₁₂, G₂₂ следующими формулами (индексы ячейки сетки 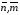опускаем):

(4.5)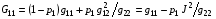

,

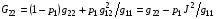
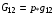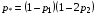
Прежде всего необходимо проверить, что матрица G положительно определена, т.е. 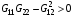при любых значениях метрических параметров g₁₁, g₁₂, g₂₂ , таких что .

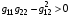В этом можно убедиться непосредственной выкладкой:

6. 

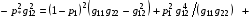
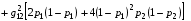
Положительность правой части при ограничениях (4.4) очевидна.

Отметим далее, что при p₁=p₂=0 из формул (4.5) получаем G₁₁=g₁₁, G₂₂=g₂₂, G₁₂=g₁₂ .В соответствии с описанным ранее для формул (1.5) получаем, что p₁=p₂=0 является неподвижной точкой описываемого семейства отображений, зависящего от двух параметров p₁ и p₂ .

Назначая эти управляющие параметры, можно реализовать различные частные случаи, уже отмечавшиеся выше. Отметим некоторые из них.

а) Если p₁=1 или p₂=0.5, то p_*=0 и G₁₂=0.

Следовательно, будут реализовываться дискретные варианты «квазиортогональных» функционалов, рассмотренных в § 2.

б) Если p₁=0, p₂=1, то p_*=-1 и реализуется специфический случай (2.13).

в) Следует особо отметить, что в случае g₁₂=0 получаем:

, ,

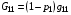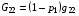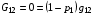
при любом значении параметра p₁ . Таким образом, любая ортогональная сетка является неподвижной точкой для рассматриваемого семейства отображений. Представляется, что это весьма ценное качество рассматриваемого алгоритма назначения управляющих метрических параметров.

4.5. Для анализа результатов численных экспериментов и их планирования оказалось полезным иметь формулы для производных подынтегрального выражения функционалов (1.1) и (1.10)-(1.11) по параметрам p₁ и p₂ . Хотя эти формулы носят несколько громоздкий характер, считаем целесообразным их привести. Выпишем их для Е^* . (Для Е дополнительный сомножитель J в знаменателе от параметров p₁ и p₂ не зависит, поэтому просто выносится за знак производной). Итак,

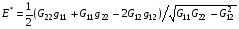
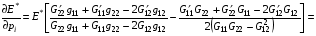
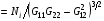, (i=1,2)

6. 

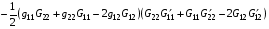
Здесь 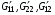представляют производные по параметру p_i величин G₁₁, G₂₂, G₁₂ соответственно. Знаки производных E^* по параметрам p₁ и p₂ определяются величинами N₁ и N₂.

Для вычисления N₁ полагаем в соответствии с (4.5):

(4.8) , , ,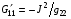

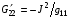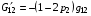а для вычисления N₂

(4.9) ,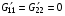

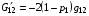
Чтобы не загромождать изложения выражениями типа формулы (4.6), ограничимся только частным случаем p₁=0. Тогда

(4.10) , ,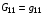

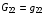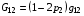
Формула (4.7) с учетом (4.8) дает для N₁ (0,p₂):

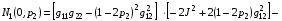
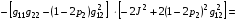
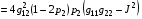
Формула (4.7) с учетом (4.9) дает для N₂ (0,p₂):

.

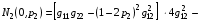
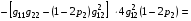
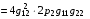Из этих формул следует, что 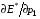и 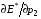в окрестности точки p₁= p₂=0 положительны, если g₁₂0 (о случае g₁₂=0 все уже сказано выше). Это согласуется с тем фактом, что при p₁= p₂=0 достигается абсолютный минимум E^*, равный 1. Обращаем внимание на смену знака производной 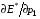при переходе на интервал 0.5< p₂<1.

§ 5. О численных алгоритмах минимизации функционалов.

5.1. Чтобы получить непосредственное представление о степени сложности уравнений, которые придется решать при минимизации вариационных функционалов, выпишем уравнения Эйлера-Лагранжа для функционала (1.1). Как уже отмечалось в § 1, эти уравнения имеют вид (1.12). Формулу для Е запишем в виде:

1. ,

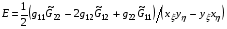где g₁₁, g₁₂ , g₂₂ определены формулами (1.2).

Метрические параметры 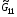, , 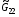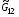будем считать функциями независимых переменных (,), хотя в соответствии с изложенными в

§ 4 вариантами их назначения следовало бы учитывать и более сложный характер их зависимости от производных x_, y_, x_, y_.

Здесь уместно напомнить о целесообразности замены якобиана в знаменателе на величину J_, определенную формулой (1.19).

Необходимые для выписывания уравнений (1.12) производные 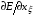, , 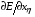, 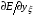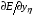получаются непосредственным дифференцированием (5.1) и после некоторых преобразований приобретают следующий вид:

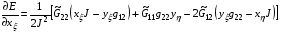
(5.2)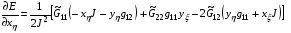

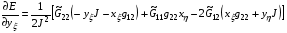
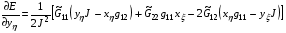
Заметим, что в частном случае гармонических отображений 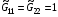, 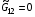формулы (5.2) заметно упрощались и, кроме того, удавалось в качестве следствия из получающихся для этого случая уравнений (1.12) получить очень изящные уравнения:

(5.3)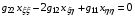

.

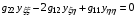Принято считать, что применение уравнений (5.3) в практике расчета сеток восходит к работе [18].

5.2. Изложение численных алгоритмов минимизации вариационных функционалов представляет весьма сложную задачу. Поэтому ограничимся в качестве иллюстрации только некоторыми простейшими случаями. В качестве первого из них рассмотрим вариационный функционал (1.10)-(1.11), дискретизация которого осуществляется без разрезания ячеек сетки на треугольники посредством использования формул (3.6)-(3.9), а в качестве метрических параметров G₁₁, G₂₂ используются вычисленные посредством интерполяции в разделе 4.2. и G₁₂=0.

Разностные уравнения, которым должны удовлетворять координаты искомой сетки (x,y)_n,m , получаются как условия равенства нулю производных соответствующей вариационному функционалу интегральной суммы:

(5.4) , , ,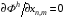

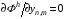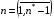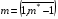
Такие уравнения выписываются для всех внутренних узлов искомой сетки, значения же координат граничных узлов предполагаются заданными. В интегральной сумме (3.9) от координат узла с фиксированным номером (n,m) будут зависеть только 4 слагаемых, отвечающих 4 ячейкам сетки с номерами 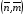, , 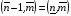, , 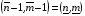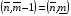согласно обозначениям, описанным в разделе 3.1. Эти 4 ячейки образуют так называемый шаблон узла. Для его описания удобно, как это предложено в работе [17], присвоить 9 узлам сетки следующие «простые» номера:

(5.5)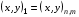

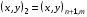
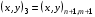
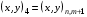
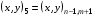
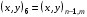
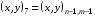
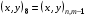
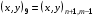
Условно доопределим .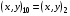

Тогда шаблон образует 4 ячейки с номерами 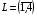, где ячейка с номером L имеет вершины с «простыми» номерами 1, 2L, 2L+1, 2L+2.

Обозначим 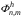«элемент» интегральной суммы Ф^h , зависящий от искомых координат 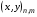. Тогда

6. ,

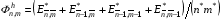где в соответствии с формулой (3.6) и с учетом G₁₂=0:

6. 

Величины 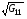, 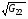вычисляются по формулам (4.2).

Для получения уравнений (5.4) достаточно дифференцировать «элемент» (5.6). Выбранная форма (3.7) для величин 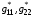позволяет получить уравнения (5.4) для описанного выше шаблона в виде:

(5.8) , .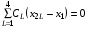

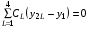Коэффициенты C_L вычисляются по формулам:

(5.9) ,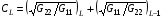

где следует полагать L-1=4 для L=1.

Вопрос о решении системы линейных уравнений (5.8), выписанных для всех внутренних узлов сетки, может быть предметом специального обсуждения. В практических расчетах нестационарных задач используется простейший вариант: выполняется несколько явных итераций, в ходе которых новое положение 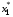, 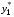узла (х₁,у₁) получается по формулам:

(5.10) ,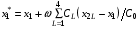

,

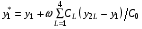где 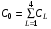, 0<<1 – некоторый коэффициент «запаса», задаваемый в качестве управляющего параметра. Конечно, это очень медленно сходящийся итерационный процесс. Простейшим способом его улучшения является использование вместо  переменной последовательности чебышевских параметров. Однако он практически работоспособен, а предметом обсуждения сейчас являются совсем другие вопросы.

5.3. В качестве второго случая численной минимизации рассмотрим случай, когда вариационный функционал задается в форме (1.10)-(1.11), а метрические параметры G₁₁, G₂₂, G₁₂ назначаются, как описано в разделе 4.3, изменяющимися в ходе итерационного процесса, например, согласно формулам (4.5).

Рассмотрим сначала случай, когда параметр p_*=0 и, следовательно G₁₂=0. Тогда для расчета сетки получаются те же формулы (5.9)-(5.10). Отличие состоит лишь в том, что при вычислении коэффициентов C_L величины G₁₁, G₂₂, как уже отмечено, назначаются по формулам (4.5) и изменяются на каждой итерации. Вместо системы линейных уравнений реализуется решение некоторой нелинейной системы. Проблему сходимости итерационного процесса и скорости, с которой это происходит, сейчас обсуждать не будем.

Обратимся к более общему случаю, когда управляющий параметр p_*0. Тогда формула (5.7) должна быть заменена на следующую:

(5.11)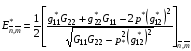

Появляющаяся в ней величина 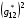аппроксимируется формулой (3.8). Выше при рассмотрении случая p_*=0 величины G₁₁, G₂₂ вычислялись по состоянию сетки на последней сосчитанной итерации и при получении уравнений (5.8) предполагались «замороженными». Наличие в формуле (5.11) величины 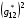в числителе и знаменателе вынуждает выбрать один из трех путей.

а) «Заморозим» 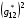и в числителе и в знаменателе. Тогда получим те же уравнения (5.8), а формулы (5.9) должны быть заменены на

, .

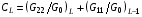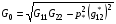Такой путь представляется весьма сомнительным.

б) «Заморозим» 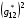только в знаменателе. Тогда в уравнениях (5.8) появятся дополнительные члены, включающие величины x_2L+1, y_2L+1 со своими коэффициентами. Конкретизировать их вид не будем.

в) Формула (5.11) порождает нелинейный функционал. Он рассматри-вается как ситуация общего вида, к обсуждению которой и перейдем.

5.4. В работе [17] представлен алгоритм прямой минимизации вариационного функционала произвольного вида. Алгоритм носит локальный характер. Для каждого узла сетки независимо решается задача отыскания его нового положения, уменьшающего значение рассматриваемого функционала, в предположении, что все другие узлы сетки при этом остаются фиксированными («замороженными»).

Схема метода спуска состоит в следующем. В рассматриваемом узле назначается направление спуска. Вычисляются коэффициенты локальной параболической аппроксимации функционала и находится точка с минимальным значением функционала на выбранном направлении. В качестве нового приближения назначается точка на выбранном направлении с некоторым коэффициентом «запаса».

Численные эксперименты (в частности, с функционалами для расчета сеток, рассматривавшимися в работе [11]) подтвердили работоспособность обсуждаемого алгоритма, хотя и крайне медленную его сходимость.

В условиях большой сложности уравнений, описанных выше в разделе 5.1., трудно усмотреть практическую альтернативу такому пути численной минимизации разработанных функционалов для построения сеток. Поэтому ограничимся изложенным.

§ 6. Разнообразие форм универсальных функционалов

и проблема неединственности решения.

6.1. Как уже отмечалось, вариационные функционалы (1.1) и (1.10)-(1.11) таковы, что позволяют при соответствующем задании входящих в них локальных метрических параметров G₁₁, G₂₂, G₁₂ воспроизвести любую наперед заданную невырожденную сетку. Это и рассматривается как основание называть их универсальными.

Совершенно очевидно, что таким же свойством будут обладать и функционалы

(6.1) ; ,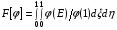

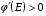в которых подынтегральное выражение Е, называемое плотностью энергии отображения, заменено на (Е), где (Е) - произвольная монотонно возрастающая функция для Е1. Нормирующий сомножитель (1) введен в (6.1) для сохранения минимума подынтегрального выражения равным 1.

Более того, если в процессе минимизации функционала (1.1) достигается его абсолютный минимум Е1, F=1, то для любого из функционалов (6.1) на той же сетке будет тоже достигаться абсолютный минимум. Однако, если это не так и абсолютный минимум функционала (1.1) не достигается, то минимизация функционалов (6.1) будет порождать другие сетки.

Как уже отмечалось, в силу большой неопределенности требований к конструируемой сетке (кроме очевидного – невырожденности) с точки зрения практики желательно иметь возможность обеспечить разнообразие возможных решений задачи.

Чего можно ожидать от задания различных функций (Е)? Если, например, использовать (Е)=E^p, то при больших значениях показателя p можно ожидать в определенной степени минимизации максимального значения величины 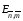по ячейкам сетки (по аналогии с тем, как в функциональном анализе норма пространства L_p при p приближается к норме пространства С). Такая постановка задачи о построении сетки может быть вполне осмысленной, поскольку зачастую качество сетки определяется одной (самой «худшей») ее ячейкой.

Еще один пример. При криволинейной форме границ области, в которой строится сетка, очень велик диапазон изменения локальных коэффициентов вариационного функционала. Это создает и усиливает затруднения при численной реализации ввиду огромных чисел обусловленности матриц для соответствующих линеаризованных задач. В этом смысле можно было бы ожидать, что использование функции (Е)=1+lnE, уменьшающей такой разброс, могло бы в какой-то степени ослабить эту тенденцию. Приведенные примеры представляют не более, чем качественные соображения или рабочие гипотезы, и нуждаются в экспериментальной проверке.

Создать универсальный алгоритм построения сеток в произвольной области, форма которой зачастую заранее неизвестна (например, получается в ходе нестационарного расчета), пока не удалось. Поэтому разумной альтернативой представляется введение в алгоритмы построения сеток небольшого числа управляющих параметров, которые позволили бы в неблагоприятных ситуациях, когда исполнителю «не нравится» сложившаяся расчетная сетка, путем их смены преодолевать «кризисные» явления. Степенной показатель p, приведенный выше в качестве примера, может рассматриваться как один из таких управляющих параметров. Другие примеры содержались в § 4 при изложении алгоритмов назначения локальных параметров G₁₁, G₂₂, G₁₂. Главное затруднение состоит в том, что действия по изменению управляющих параметров должны быть целенаправленными. Пока же приходится лишь ссылаться на пресловутый «опыт вычислителя».

6.2. Это одна сторона вопроса. Вторая состоит в том, что никакая свобода в алгоритме не должна отменять детерминированного характера его работы – иначе начнется хаос (это напрямую связано с корректностью математической постановки задачи) и не останется никакой надежды на благополучное проведение расчета на ЭВМ.

Между тем ситуация складывается очень непростая. В частности, в упоминавшейся уже работе [6] отмечается, что, поскольку используемый вариационный функционал является невыпуклым, он может иметь несколько стационарных точек. По мнению авторов [6], «увеличение количества узлов сетки (т.е. приближение к дифференциальной постановке задачи) не всегда приводит к уменьшению количества таких точек. Ситуация часто бывает обратной и, по-видимому, можно построить примеры конфигураций областей, когда количество стационарных точек исчисляется десятками и сотнями».

Между тем, как уже отмечалось в разделе 2.6., в работе [2] доказано, что для функционала (1.1) существует единственное решение в случае, если метрические параметры G₁₁, G₂₂, G₁₂ обеспечивают его абсолютный минимум. Случай, когда в процессе минимизации абсолютный минимум не достигается, оставлен открытым.

Изложенные факты позволяют выдвинуть две версии.

Первая состоит в том, что функционал (1.18), используемый в [6], «хуже», чем (1.1). Автор имеет опыт работы с другими функционалами и уже высказывал некоторые соображения по поводу возможной неединственности решения в работах [8] и [9].

Вторая версия состоит в том, в неединственности повинен итерационный процесс минимизации функционала, который может «застревать» в точках, даже не имеющих отношения к решению рассматриваемой задачи. Такая ситуация рассматривалась автором в связи с расчетами критических параметров реакторов методами, опиравшимися на известный вариационный принцип В.С.Владимирова (приводить соответствующие ссылки нет необходимости). Ситуацию удалось смоделировать на простейшем примере задачи вычисления наибольшего собственного значения симметричной матрицы 3-го порядка А с постоянными элементами, реализуемой как поиск максимума нелинейного отношения (Ax,x)/(x,x), где x – трехмерный вектор. В работе [19] приведен пример итерационного процесса, внешне вполне «безобидного», который может сходиться к ответу, не имеющему никакого отношения к делу.

Уместно заметить, что для функционала (1.10)-(1.11) без якобиана искомого отображения в знаменателе ситуация безусловно так не обостряется, как в случае функционала (1.1). Во всяком случае, при фиксированных (предписанных заранее) значениях G₁₁, G₂₂, G₁₂ (как элементах положительно определенных симметричных матриц в каждой точке , параметрического квадрата Q) вопрос о единственности искомого решения не вызывает сомнений (по-видимому, следует оговорить исключение специально конструируемых примеров).

Заключение

Подводя итог изложенному, можно констатировать, что в настоящей работе рассмотрены некоторые вариационные функционалы, которые позволяют в результате их дискретизации и последующей минимизации получить произвольную невырожденную сетку. Рассмотрены алгоритмы назначения или определения в ходе итерационного процесса входящих в функционалы метрических параметров сетки. Специальное внимание уделено вопросам конструирования ортогональных сеток (в предположении, что таковые существуют при рассматриваемой постановке задачи) или близких к ним («квазиортогональных») сеток. Кратко обсужден вопрос о конструировании численных алгоритмов для минимизации функционалов.

Следует отметить, что построение сетки не является самоцелью. Получаемая сетка будет использоваться для решения тех или иных задач математического моделирования физических процессов. В силу неопределенности требований к конструируемой сетке (кроме очевидного – невырожденности) с точки зрения практики желательно иметь возможность обеспечить разнообразие возможных решений задачи о построении сетки. В определенной степени этого можно достигнуть путем введения в алгоритмы расчета сеток некоторых управляющих параметров.

Еще одна сторона проблемы, особенно важная при решении нестационарных задач, касается того, чтобы в процессе расчета и особенно в моменты «переключения» алгоритмов это происходило «мягко и плавно». В противном случае большие, переменные по времени, скорости движения узлов сетки (по сравнению с реальными, вызванными физическими условиями задачи) могут привести к непозволительным ошибкам в моделировании физического процесса или вообще к аварийным ситуациям. Рассмотрение этих вопросов осталось за рамками настоящей работы и требует специального обсуждения.

В целях устранения главной причины, препятствующей получению ортогонального отображения и, как следствие, получению сеток, действительно близких к ортогональным, целесообразно рассматривать также возможность движения узлов сетки по некоторым границам расчетной области, как было отмечено в разделе 2.5.

Заметим также, что в работе [1] рассматривался и вариационный функционал, содержащий возможность адаптации к заданной функции f(x,y) , а также к построению сеток на поверхностях. Наконец, в [1] были сделаны некоторые предложения по обобщению функционала на трехмерный случай. Отметим также работу [20], в которой рассматривались функционалы для построения сеток на n-мерных гиперповерхностях в (n+r)-мерном пространстве.

Автор выражает благодарность Г.Б.Алалыкину за участие в проведении численных экспериментов по апробации описанных алгоритмов и М.С.Гавреевой за помощь в оформлении настоящей работы.

Литература

1. Иваненко С.А. Управление формой ячеек в процессе построения сеток.// ЖВМ и МФ, 2000, т.40, № 11, 1662-1684.

2. Иваненко С.А. О существовании уравнений для описания классов невырожденных криволинейных координат в произвольной области //ЖВМ и МФ, 2001, т.41, №8.

3. Годунов С.К., Прокопов Г.П. – О расчетах конформных отображений и построении разностных сеток.// ЖВМ и МФ, 1967, т.7, № 5, 1031-1059.

4. Численное решение многомерных задач газовой динамики. Под общей редакцией С.К.Годунова.//М., «Наука», 1976, 400 стр.

5. Годунов С.К. Воспоминания о разностных схемах. Доклад на Международном симпозиуме «Метод Годунова в газовой динамике». Мичиганский университет (США). Май 1997//Новосибирск. Научная книга, 1997, 40 стр.

6. Гаранжа В.А., Капорин И.Е. – Регуляризация барьерного вариационного метода построения разностных сеток.// ЖВМ и МФ, 1999, т.39, №9, 1489-1503.

7. Прокопов Г.П. Конструирование тестовых задач для построения двумерных регулярных сеток.//Вопросы атомной науки и техники. Серия: Мат. моделирование физ. процессов. 1993, вып.1, 7-12.

8. Прокопов Г.П. Методология вариационного подхода к построению квазиортогональных сеток.// Там же, 1998, вып.1, 37-46.

9. Прокопов Г.П. О расчете разностных сеток, близких к ортогональным, в областях с криволинейными границами.// Препринт ИПМ АН СССР, 1974, №17, 36 стр.

10. Сидоров А.Ф., Шабашова Т.И. Об одном методе расчета оптимальных разностных сеток для многомерных областей.// Числ. методы механики сплошной среды. Новосибирск, ИТПМ СО АН СССР, 1981, т.12, №5, 106-124.

11. Антонова Р.Н., Прокопов Г.П. Расчет квазиортогональных сеток минимизацией вариационных функционалов.//Препринт ИПМ РАН, 1998, № 31, 32 стр.

12. Белинский П.П., Годунов С.К., Иванов Ю.Б., Яненко И.К. Применение одного класса квазиконформных отображений для построения разностных сеток в областях с криволинейными границами.// ЖВМ и МФ, 1975, 15, №6, 1499-1511.

13. Годунов С.К., Гордиенко В.М., Чумаков Г.А. Квазиизометрическая параметризация криволинейного четырехугольника и метрика постоянной кривизны. Siberian Advances in Mathematics, 1995, т.5, №2, 1-20.

14. Godunov S.K., Zhukov V.T., Feodoritova O.B. An algorithm for construction of quasi-isometric grids in curvilinear quadrangular regions.// Proc. 16-th Internal. Conf. on Numer. Meth. Fluid Dynamics. Arcachon, France, July 6-10, 1998, p.49-54.

15. Антонова Р.Н., Прокопов Г.П. Сравнение нескольких вариантов построения двумерных разностных сеток посредством интерполяционных формул.//Вопросы атомной науки и техники. Сер.: Мат. моделирование физ. процессов, 1994, вып.2, 78-88.

16. Антонова Р.Н., Прокопов Г.П. Расчет подвижных сеток и проблема начального приближения для сетки в сложной области.// Там же, 1996, вып.1-2, 84-90.

17. Антонова Р.Н., Прокопов Г.П. Расчет гладких сложносоставных сеток прямой минимизацией вариационных функционалов.// Вопросы атомной науки и техники. Сер. Мат. моделирование физических процессов. 1997, вып. 2, 17-23.

18. Winslow A.M. Numerical solution of the quasi-linear Poisson equation in a non uniform triangle mesh.// J. Comp. Phys. 1966, vol.1, № 2, 149-172.

19. Прокопов Г.П. Об одном методе отыскания максимального собственного значения симметричной матрицы.// ЖВМ и МФ, 1967, т.7, № 5, 1167-1171.

20. Лисейкин В.Д. О конструировании регулярных сеток на n-мерных поверхностях. // ЖВМ и МФ, 1991, т.31, №11, 1670-1683.