«Действия с многочленами» 7 класс

Урок по алгебре «Действия с многочленами» 7 класс

Скажи мне и я забуду,

покажи мне и я запомню,

дай мне действовать самому и я научусь.

Конфуций

Цели и задачи:

Образовательная: проверить знания, умения и навыки учащихся по теме «Действия с многочленами»
Воспитательная: воспитывать интерес к алгебре, применяя интересные задания, используя различные формы работы; формирование личностных качеств: точность и ясность словесного выражения мысли; сосредоточенность и внимание; настойчивость и ответственность
Развивающая: развивать умение учащихся работать как индивидуально (самостоятельно), так и коллективно (работа в парах); развивать познавательные интересы.

ХОД УРОКА

1. Организационный момент

Здравствуйте ребята и уважаемые гости. Сегодня на уроке мы с вами продолжим изучение темы «Действия с многочленами!».

Цель нашего урока повторить и обобщить теоретические знания по данной теме и продолжить работу по обработке умений и навыков выполнения “Действия с многочленами».

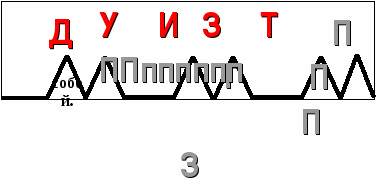
Перед вами Маршрут путешествия по вершинам знаний

на тему «Действия с многочленами».

Давайте начнем заполнять.

1.Графический тест теоретического материала

Верно ли утверждение, определение, свойство?

Одночленом называют сумму числовых и буквенных множителей.

2. Одночлены, которые отличаются друг от друга только коэффициентами,
называются подобными членами.

3. Алгебраическая сумма нескольких одночленов называется многочленом.

1. Буквенный множитель одночлена, записанного в стандартном виде,

называют коэффициентом одночлена.

2. Когда раскрываем скобки, перед которыми стоит знак “-”, скобки

опускаем, и знаки членов, которые были заключены в скобки, меняют

на противоположные.

3. В результате умножения многочлена на многочлен получается

многочлен.

1. Чтобы разделить многочлен на одночлен, нужно каждый член многочлена

умножить на этот одночлен и полученные результаты сложить.

2. Сумма показателей степеней всех букв входящих в одночлен

называемый степенью одночлена.

3. Многочлен в котором отсутствуют подобные члены и каждый из них

одночлен стандартного вида называется многочленом стандартного

вида.

(Графический диктант ^ - да, — нет)

Выставьте себе оценки: «5» - ошибок нет

«4» - одна ошибка

«3» - две ошибки

«2» - три ошибки

___________

Вершина «Д»-домашняя работа

Итак, маршрут готов. Отправляемся покорять вершину «Д» - домашняя работа. Соотнесите ответы на экране с номерами заданий. (пауза) Отметьте в маршрутном листе, как справились с д/з.

- Ребята, среди перечисленных выражений на экране назовите одночлены. А как называются остальные выражения?

5 заданий правильно – 3 балла

4- 3 заданий – 2 балла

2 задания – 1 балл

Вершина «У» - устная работа

1. 1) Замените букву «М» многочленом так, чтобы полученное равенство было верным:

5а + М = 5а + 3b – 8;
b² – bc - М = b² – bc – 7b + 5;

М + ( 2a² + 4b – b²) = 3a² + 4ab.

2) В пустое окошко вставьте одночлен так, чтобы полученное равенство было верным:

· (a – b) = 4ac – 4bc;

(12a³ – 4a²) : = 3a – 1;

· (2a – b) = 10a² – 5ab.

слайд( 9 )

2.Соедините отрезками одночлены в левом столбце с соответствующими одночленами в стандартном виде в правом столбце.

3ав4а²

8,4а³в²

1,5в²4а³

6а³в

1,2а³5в

6а³в²

7а²в1,2ав

12а³в

Вершина «И» -историческая справка

Историческая справка

Историческую справку о многочленах нам подготовила…( )

1ученик

Тема “Многочлены” - очень важная тема в алгебре. Многие ученые работали над этой темой. В 1799 г. немецкий ученый Гаусс доказал основную теорему алгебры многочленов с комплексными коэффициентами, в конце XVIII в. французский математик Безу доказал основную теорему многочленов с действительными коэффициентами.

2 ученик

М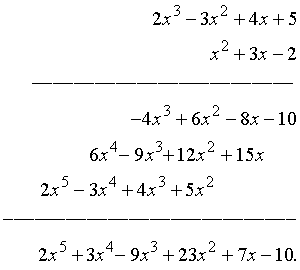ногочлен - это алгебраическая сумма одночленов. А одночлен - произведение числовых и буквенных множителей. Одночлен обычно считают частным случаем многочлена. Одночлен – это многочлен, в состав которого входит всего один член, и его называют – моном. Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена: если их два, то говорят, что дан двучлен, или бином, например 2а+в. Если их три, то говорят – трёхчлен или трином, например 2x³ – 5x² +с. Говорят, в Африке есть племя, считающее так: 1,2,3, много. Наша терминология применительно к многочленам напоминает африканскую. Если слагаемых, т. е. одночленов больше трёх, то говорят просто многочлен.

О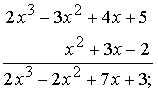бычно многочлен обозначают буквой «р» – с этой буквы начинается греческое слово «polys»– «многий», «многочисленный», многочлены в математике называют также полиномами. Многочлены можно складывать и умножать так же, как числа. Например, чтобы найти сумму многочленов 2x³ – 3x² + 4x + 5 и x² + 3x – 2, можно записать так…

Чтобы найти произведение тех же многочленов, мы записываем так… И производим сложение и умножение, как с числами.

Спасибо!

Вершина «З» - задача

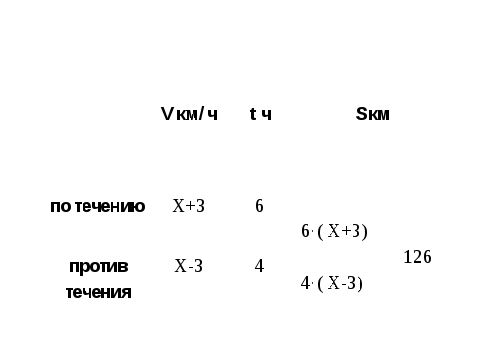
Пусть х км/ч- скорость лодки ,тогда (х+3)км/ч-скорость лодки по течению,

(х-3)км/ч скорость лодки против течения. Знаем, что всего лодкой пройдено расстояние 126км.

Составляем уравнение: 6(х+3)+4(х-3)=126

6х+18+4х-12=126

10х=126-18+12

10х=120

х= 12

12 км/ч – скорость лодки.

Ответ: 12 км/ч

(в маршрутном листе отметить правильность составления уравнения)

Зарядка для глаз по Аветисову

Вершина «Т»

Если есть компьюторы в классе то можно использовать программу My TestS на уроках математики .Оценки выставляет компьютер, а не учитель, что исключает, если так можно выразиться, человеческий фактор (при этом исключаются всяческие обвинения в адрес учителя по поводу заниженных отметок).

Если нет то

( Разноуровневая самостоятельная работа, карточка зеленого цвета, соответствует отметке «3», синего цвета – отметке «4»,

красного цвета – отметке «5»).

Вариант – 1

(зеленый цвет)

Упростите выражение 1 – 6:

1. (7х – 4) – (1 – 2х)

6) 9х – 5; 10) 5х – 5; 3) 9х – 3.

2. – 3х³ · ху²

1) – 3х³у²; 17) 3х³у²; 12) – 3х⁴у² .

3. (3х²– 2х + 5) · 4х³

5) 12х⁶ – 8х⁴ + 20х³; 18) 12х⁵ – 8х⁴ + 20х³; 11) 12х⁵ + 8х⁴ + 20х³.

4. 3а (а + 1) – а²
9) 3а² + 1 – а²; 2) 2а² + 3а; 16) 2а² – 1.

5. (х + 1)(х – 1)
7) х² – 1; 13) х² – 2х – 1; 4) 1 - х².

6. Упростите выражение: (7 m² – 20mn – 10m) : (10m)

15)0,7m – 2n – 1; 8) 70m³ – 2n – m; 14) 0,7m – 2m – 1.

(Учащиеся выбирают соответствующий цвет карточки и выполняют самостоятельную работу. Цифру, под которой записан правильный ответ надо подчеркнуть в контрольном талоне. Решение записать в тетрадь.)

Контрольный талон

3н

1к

5а

2а

4г

8а

6д

12е

11м

9и

7р

14л

10э

17р

18к

16е

13т

15т

Вариант – 1

(синий цвет)

Упростите выражение 1 – 6:

1. (4ху - 3х²) – ( - ху + 5х²)

3) 5ху – 8х³; 10) 3ху + 2х² ; 6) 5ху – 8х² .

2. – 4а²b ·(- ab²)
1) – 2a³b³; 17) 12a²b²; 12) 2a³b³.

3. 12a²(a⁵ – a⁴ – 2a³)
5) 12a¹⁰ – 12a⁸ – 24a⁶; 11) 12a³ – 12a² – 24a; 18) 12a⁷ – 12a⁶ – 24a⁵.

4. (x + 1)(x² + x – 1)

2) x³ + 2x² – 1; 9) x³ + 2x² – 2x – 1; 16) x³ – 2x – 1.

5. (a – 2)(a + 2) – a(a + 1)

4) 4a – 1; 7) – 4 – a; 13) 4 – a.

6. (18a⁴ – 27a³) : (9a²) – (10a³) : (5a)

15) – 3a; 8) a⁴ – 3a; 14) – a² – 3a.

(Учащиеся выбирают соответствующий цвет карточки и выполняют самостоятельную работу. Цифру , под которой записан правильный ответ надо подчеркнуть в контрольном талоне. Решение записать в тетрадь.)

Контрольный талон

3н

1к

5а

2л

4г

8а

6е

12в

11м

9и

7и

14л

10э

17р

18к

16е

13т

15д

Вариант – 1

(красный цвет)

Упростите выражение 1 – 6:

1. (5,5х³у – 2ху²) – (0,5х³у – 2ху²)
6) 5х³у; 3) 5х³у – 4ху²; 10) 5х³у + 4ху².

2.

1) 10х³у³; 12) х³у³; 17) – 10х³у².

3. )

5) 6х⁸у – 3х⁴у² + х²у⁶; 18) - 6х⁶у + 3х⁴у³ - х²у⁶; 11) 5х⁶у - 3х⁴у³ + х²у⁶.

4. (х⁴ – х³ – х² – 1)(х + 1)

2) х⁵ - 2х³ – х² – х – 1; 9) х⁵ + 2х³ + х² – х + 1; 16) х⁵ + 2х³ - х² + х + 1.

5. (1 – у)у – (у + 3)(у – 3) - у

7) 9 – 2у²; 4) 9 – у² – у; 13) 2у² + 9.

6. (3х³ + 4х²у) : х² – (10ху + 15у²) : (5у)

8) 5х + у; 14) х + 7у; 15) х + у.

(Учащиеся выбирают соответствующий цвет карточки и выполняют самостоятельную работу. Цифру , под которой записан правильный ответ надо подчеркнуть в контрольном талоне. Решение записать в тетрадь.)

Контрольный талон