Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №30 им. Н.Н. Колокольцова»

Кемеровской области Калтанского городского округа пос. Малиновка

Конспект урока по алгебре и началам анализа

в 10 классе (профильный уровень)

«Уравнение и неравенства с модулем»

подготовила

учитель математики

Кононенко Марина Геннадьевна

Калтанский ГО

2013

План-конспект урока по алгебре и началам анализа (профильный уровень).

Тема: Решение уравнений и неравенств с модулем.

Тип урока: Урок совершенствования умений и навыков.

Цели урока:

дидактическая: научить применять полученные знания при решении заданий повышенного уровня сложности, стимулировать учащихся к овладению рациональными приёмами и методами решения;

развивающая: развивать логическое мышление, память познавательный интерес, вырабатывать умение анализировать и сравнивать.

воспитательная: развивать аккуратность и трудолюбие, продолжить формирование навыков контроля и самоконтроля.

Этапы урока и их содержание

Время

(мин)

Деятельность

учителя

учащегося

1. Организационный этап

2. Постановка цели

Сегодня на уроке мы продолжим отрабатывать навыки решения уравнений и неравенств с модулем, используя как традиционные методы, так и нестандартные подходы

3. Проверка домашнего задания [3]

На дом вам было предложено решить уравнения

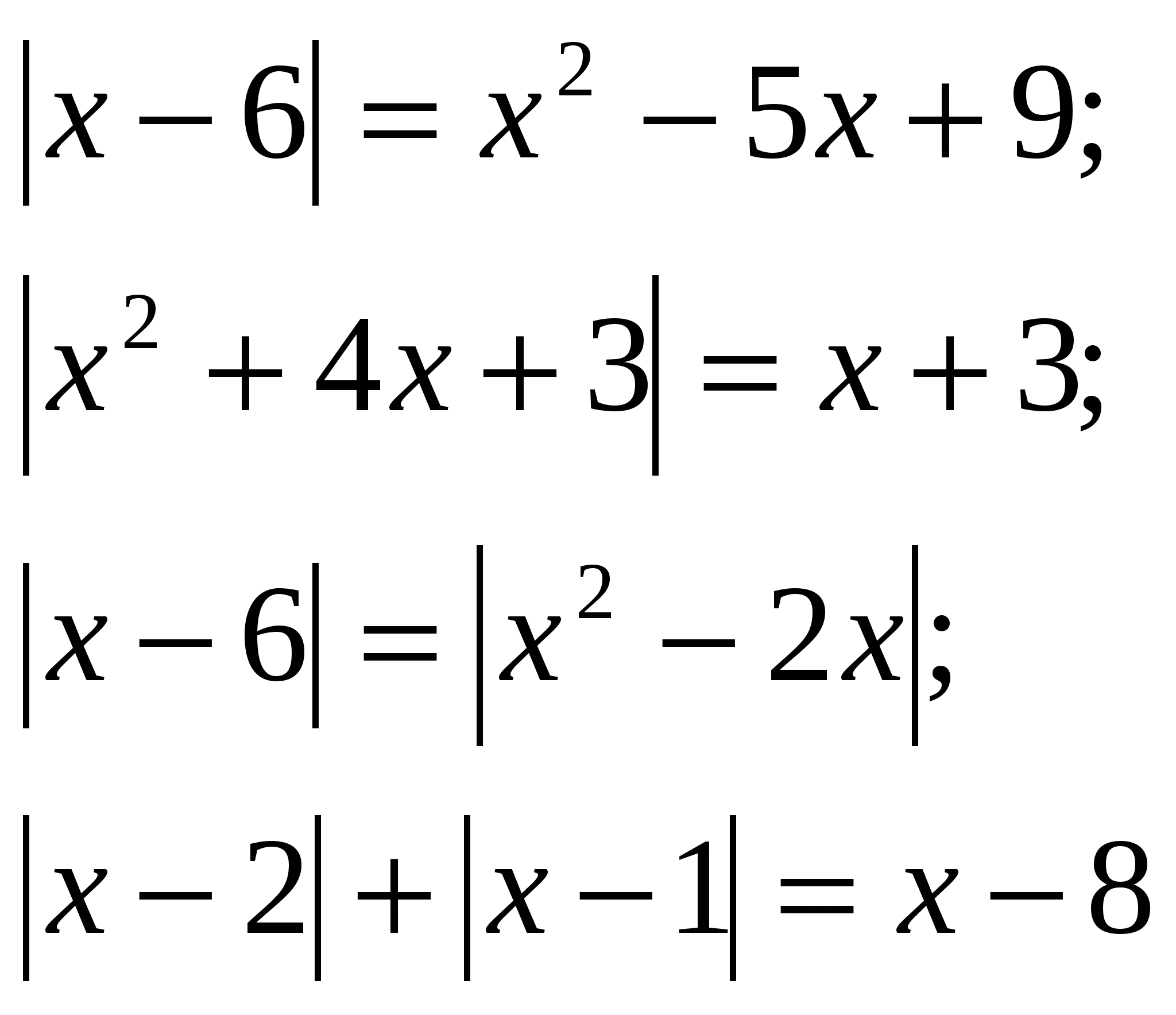
и неравенства

различными способами. Посмотрим ваше решение

4. Выполнение упражнений.

Многообразие приёмов решения задач с модулем подталкивает нас к выбору более рационального из них при решении конкретных уравнений или неравенств.

№ 1. (устно)

Решить уравнение

Решение (на основе аналитического определения модуля) [1].

Т.к. , то

х² -6х-7-1.

№ 2 Решить уравнение

Решение (применение геометрической интерпретации модуля).

На геометрическом языке: требуется найти точки с координатами х такие, что сумма расстояний от этих точек до точек с координатами -1 и 1 равна 2. Очевидно, что эти точки располагаются на отрезке

Ответ: .

№ 3 Решите неравенство

cos x1+.

Решение (функционально графический метод).

Обе части неравенства определены на R. Левая часть неравенства принимает значения из отрезка , а значения правой части составляют луч [2]. Следовательно, исходное неравенство может иметь решение только, если выполняется система

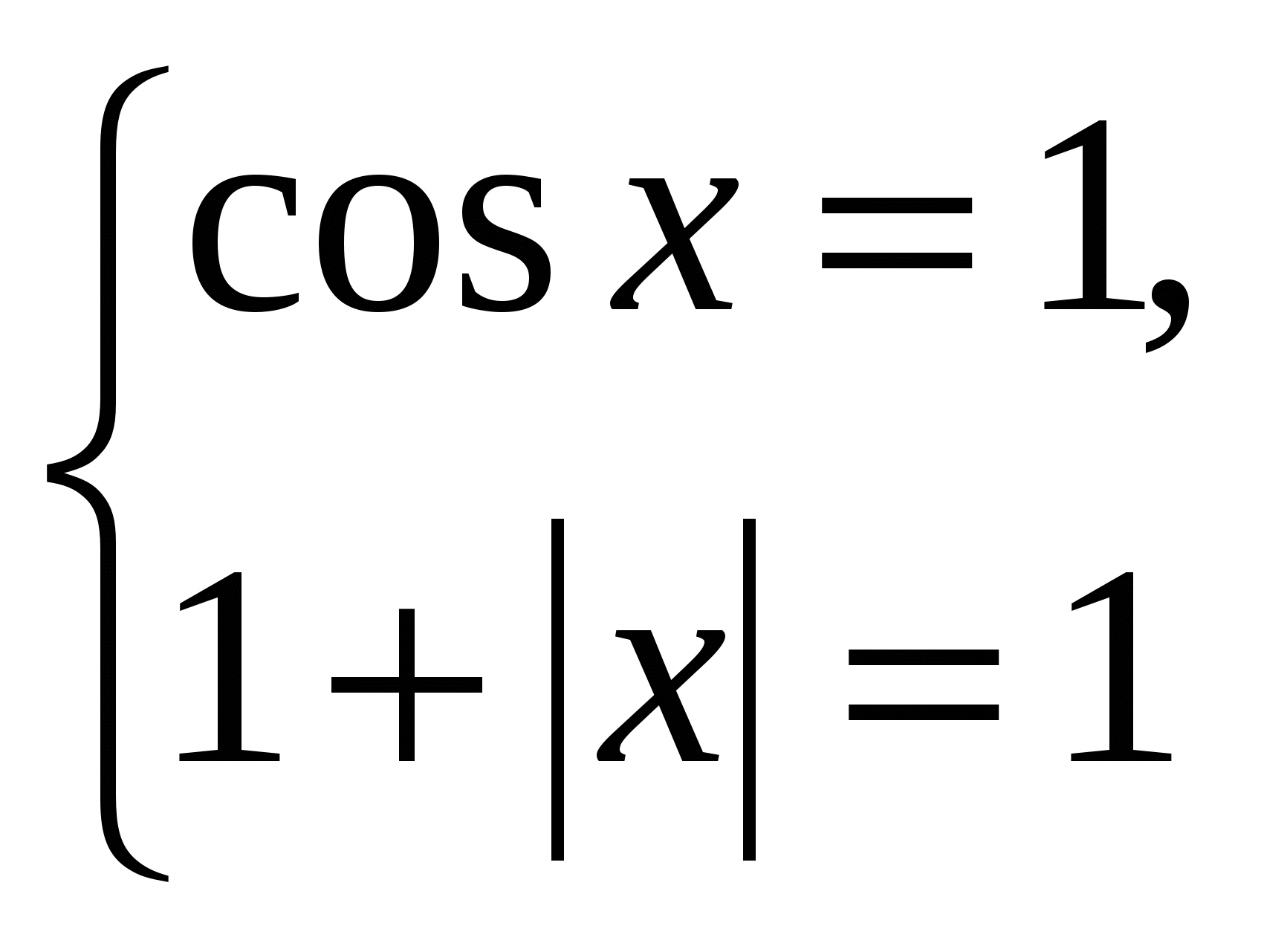
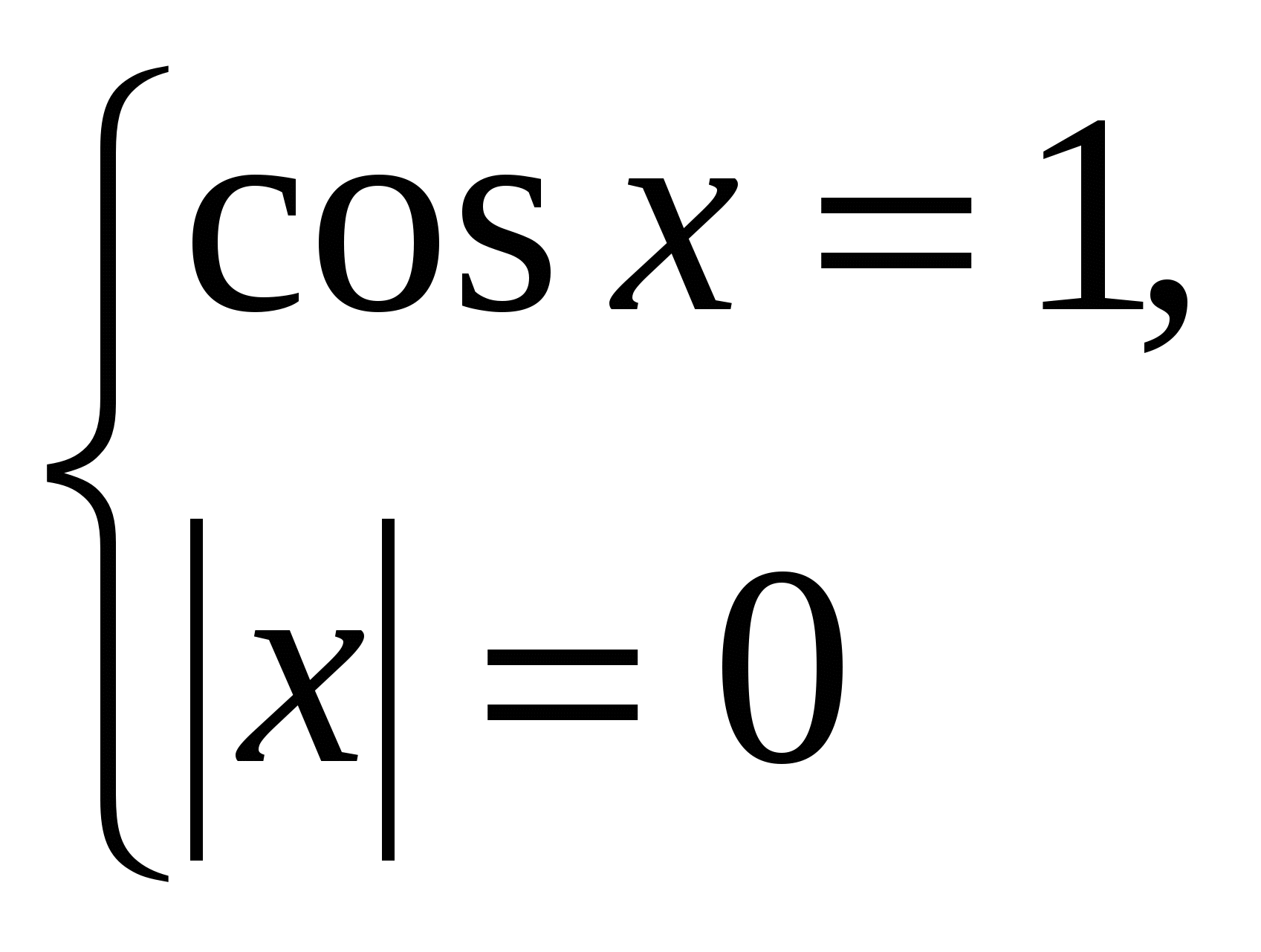
х=0.

Ответ: 0

№ 5 Решить неравенство .

Решение (метод интервалов).

Пусть f(x)= , тогда

D_f = (-∞;-1)(-1;2) (2;+∞).

Решим уравнение f(x)=0. Получим:

2=х²-х-2

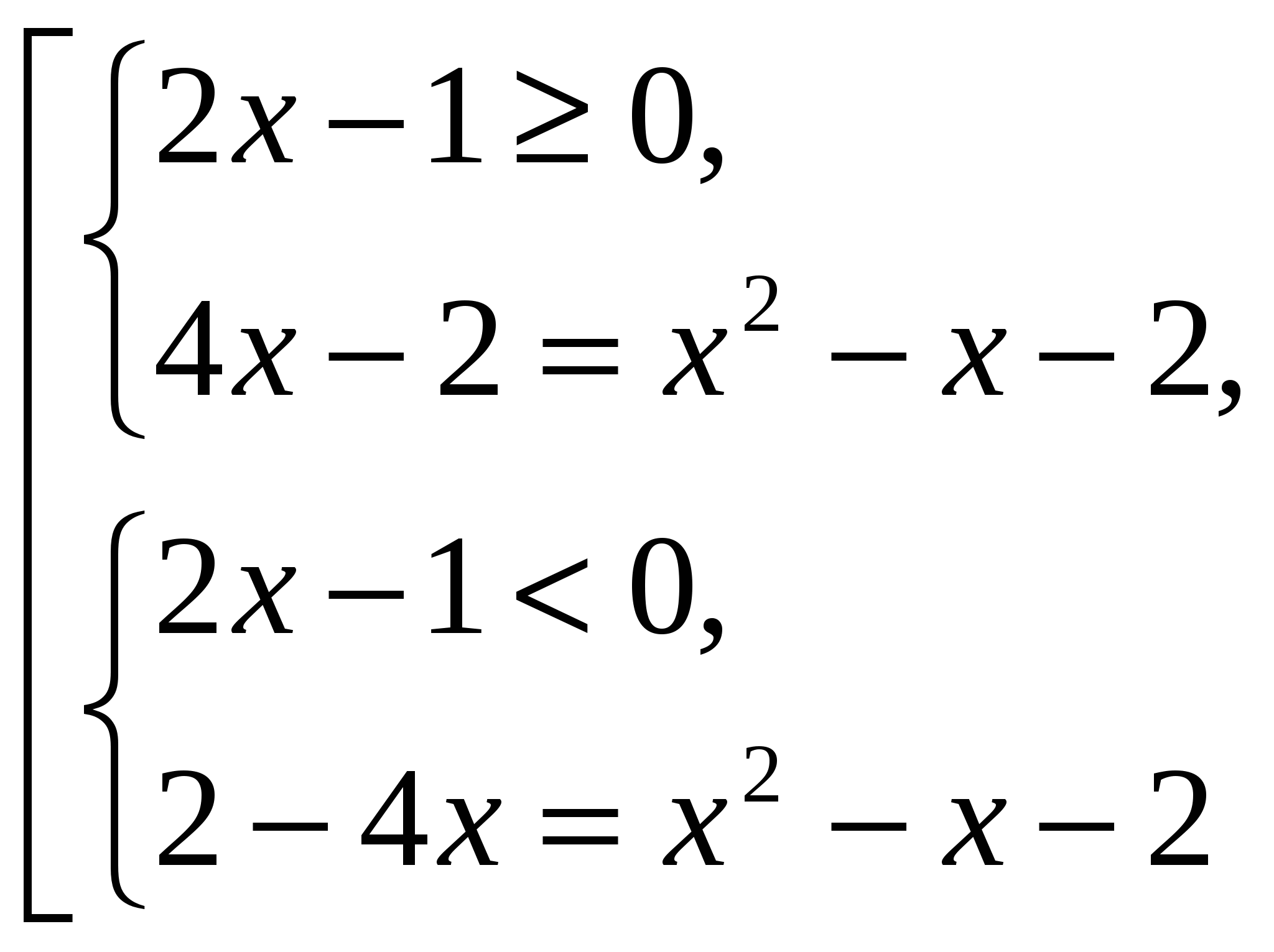
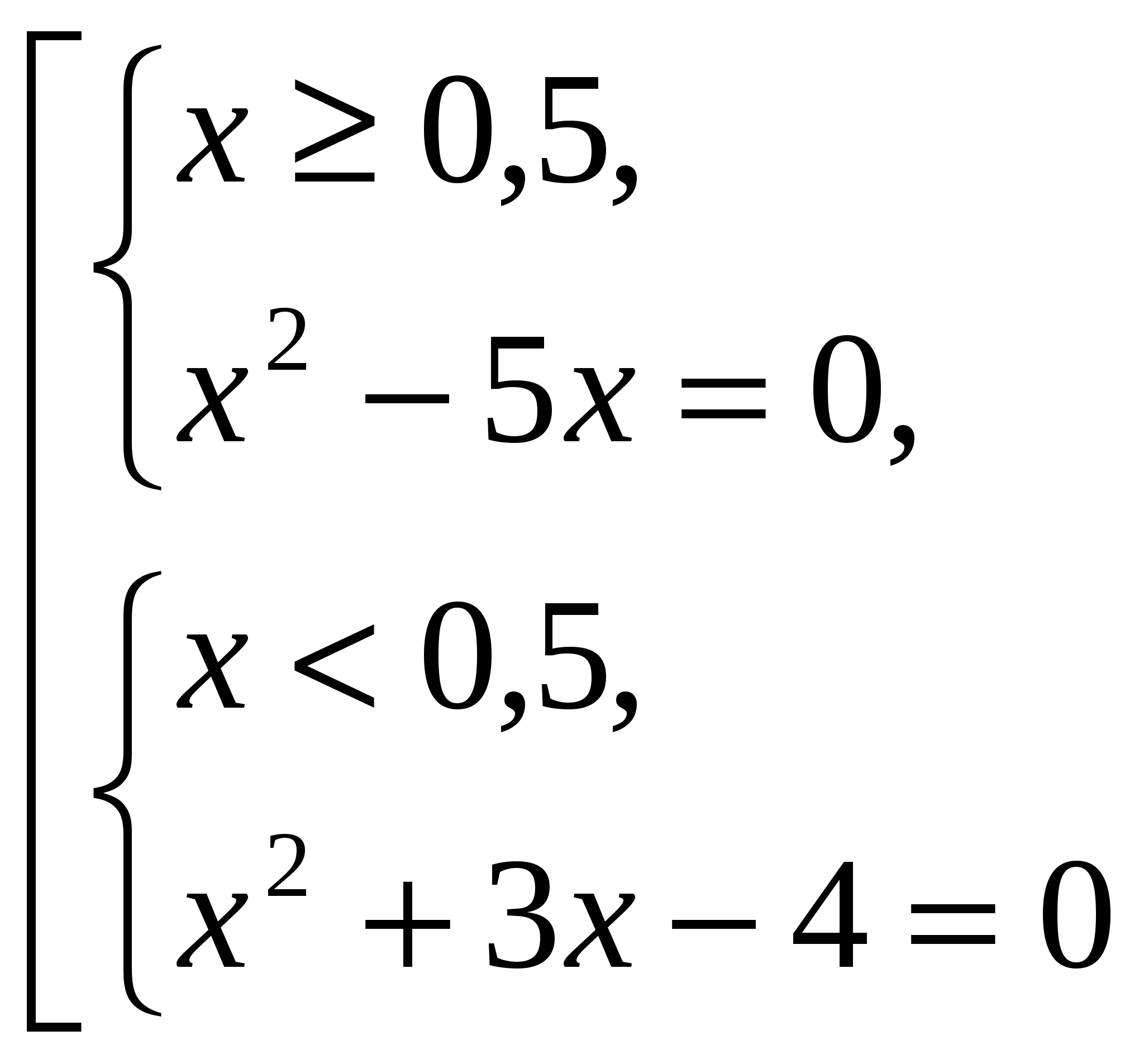
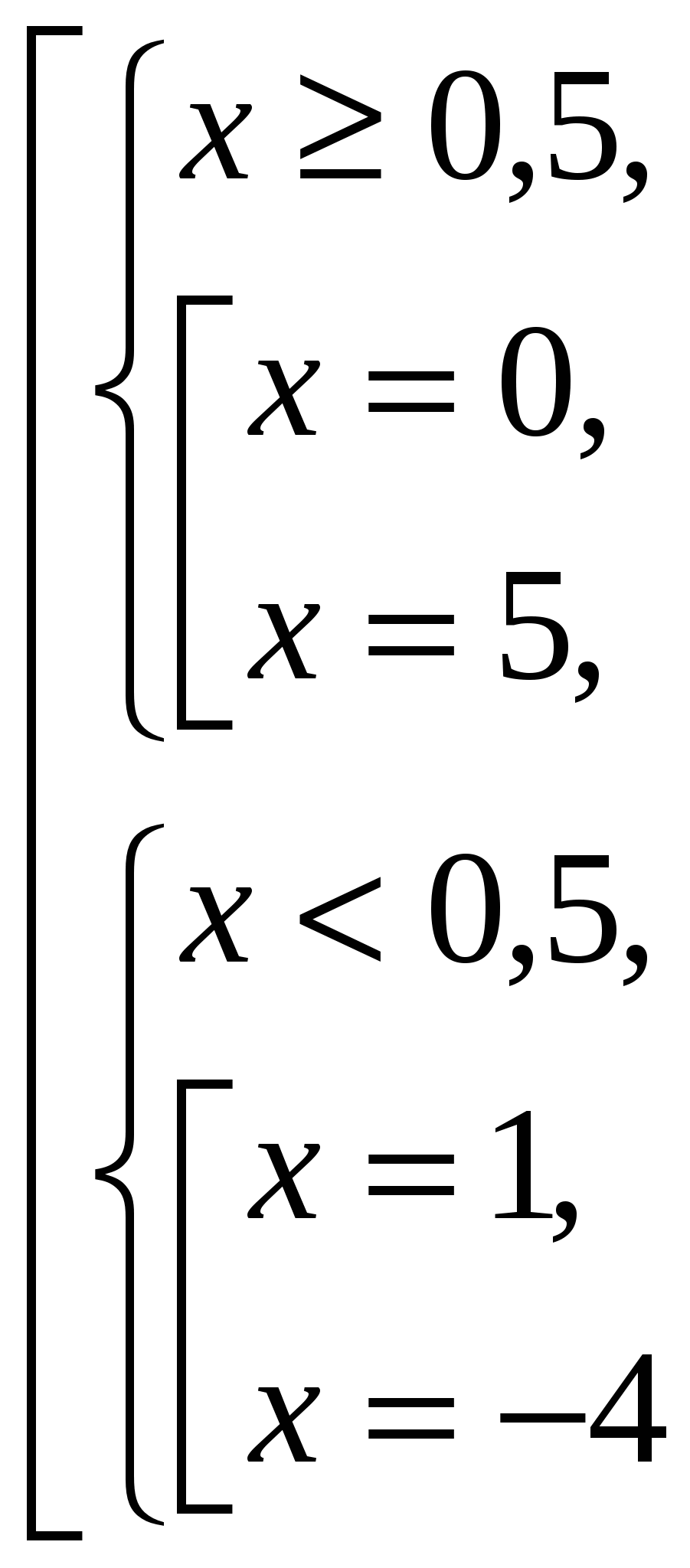
Осталось установить знак f(x) на промежутках: (-∞;-4), (-4;-1), (-1;2), (2;5), (5;+∞).

Ответ: (-4;-1)(2;5).

5. Домашнее задание

1) Решить неравенство

3) Решить уравнение

(приложение №4)

6. Подведение итогов урока.

Решение уравнений и неравенств с модулем требует от учащихся глубоких теоретических знаний, умений применять их на практике, требует внимания трудолюбия, сообразительности. Наверное,

поэтому такие задания и включены в материалы ЕГЭ.

1

3

10

7

6

5

8

3

2

Организационная

сообщает тему урока, дату проведения, цель урока

Если учащиеся не готовы показать все способы, то решение показывается на экране интерактивной доски,(приложение 1).

Вызывает по желанию 7-х человек к доске, параллельно проводит фронтальную беседу по теоретическим вопросам (приложение 2) Выставляет оценку за д/з.

Направляет на выбор рационального метода решения

Совместно с учащимися выбирает метод решения уравнения.

Следит за грамотным решением предложенного уравнения и одновременно проверяет индивидуальные решения уравнений у учащихся работающих на боковой доске по карточке, выставляет оценки за работу[1].

Направляет на выбор рационального метода решения

Обсуждает совместно с учащимися метод решения неравенства, следит за грамотностью рассуждений учащихся и верной записью решения неравенства. Выставляет оценку за работу[2].

Поясняет домашнее задание, обращая внимание учащихся на то, что аналогичные задания были разобраны на уроке.

Первое неравенство можно решить методом интервалов, второе уравнение –графически, а третье-с помощью аналитического определения модуля, рассматривая три случая (подмодульное выражение больше нуля, равно нулю и меньше нуля ) отдельно.

Сегодня на уроке все очень хорошо поработали, 10 человек получили оценки. Молодцы ребята!

Сообщают об отсутствующих

записывают в тетради

7 учащихся работают у доски, остальные принимают активное участие в устном теоретическом опросе

Предлагают методы решения, один учащийся устно объясняет решение уравнения №1.

2 человека работают на боковой доске индивидуально (приложение №3), остальные записывают в тетрадь решение уравнения №2.

Один ученик решает неравенство № 3.

Остальные участвуют в выборе рационального метода решения неравенства. Записывают решение в тетрадь.

Один ученик решает у доски, остальные записывают решение неравенства №5 в тетради.

Внимательно прослушав пояснение учителя, записывают домашнее задание.

Список использованной литературы

1. Башмаков М.И. Методические рекомендации по использованию учебника / М.И. Башмакова - “Алгебра и начала анализа. 10-11 классы” при изучении математики на базовом и профильном уровне. – М.: Дрофа, 2004. – 48 с.

2. Зеленский А.С., Панфилов И.И. Решение уравнений и неравенств с модулем. – М.: Научно технический центр «Университетский»: Универ-Пресс, 2009.– 112с.

3. Мордкович А.Г. Алгебра и начала анализа. 11 кл.: Учеб. для общеобразоват. учреждений (профильный уровень). – М.: Мнемозина, 2007. – 288 с.