Исследование функций
Исследование функций
1. Находим область определения.
Например, y=lnx определена для x>0, y=x для x≥0, y=1x для x≠0, y=ex для x∈ℝ, ℝ - множество действительных чисел, (-∞,+∞), от минус бесконечности до плюс бесконечности.
2. Находим точки пересечения с осями координат.
x=0, y = ? y=0, x = ?
3. Находим точки разрыва, исследуем на непрерывность.
Например, для y=1x x = 0 - точка разрыва, y=ex непрерывна на всей числовой оси.
4. Исследуем на чётность и нечетность.
Например, y=1x - нечётная, так как y(-x) = -1x = -y(x).
5. Исследуем на периодичность.
Например, для y=cosx период равен T=2π.
6. Находим асимптоты.
Вертикальные асимптоты находятся с помощью односторонних пределов в точках разрыва из пункта 3, горизонтальные и наклонные асимптоты находятся по формулам: y=kx+b, k=limx→∞yx, b=limx→∞(y-kx).
7. Исследуем на монотонность, находим интервалы возрастания и убывания, находим первую производную.
8. Находим вторую производную, точки перегиба и интервалы выпуклости, вогнутости.
9. Строим график.
Построение графиков
Построение можно выполнить на основе проведенного анализа, можно с помощью программы для построения графиков, скачать и использовать которую можно бесплатно.
Вы можете нам отправить задание по дифференциальному исчислению или заказать решение контрольной работы по математическому анализу.
Рассмотрим пример для y=1-x33.
D(y)=ℝ. Общего вида, т.е. ни чётная, ни нечётная.
x=0→y=1;y=0→x=1⇒A(0,1),B(1,0) - точки пересечения с осями координат.
k=limx→∞1-x33x = limx→∞1x3-13=-1,
b = limx→∞(1-x33+x) = limx→∞(1-x33+x)((1-x3)23+x2-x1-x33)(1-x3)23+x2-x1-x33= limx→∞1-x3+x3(1-x3)23+x2-x1-x33 = limx→∞1(1-x3)23+x2-x1-x33=0.
y=kx+b⇒y=-x - наклонная асимптота.
y' = 13(1-x3)-23·(-3x2) = -x2(1-x3)-23<0⇒функция убывает на ℝ, экстремумов нет.
y'' = -2x(1-x3)-23+x2·23(1-x3)-53·(-3x2) = -2x(1-x3)-23-2x4(1-x3)-53 = -2x(1-x3)53
y''=0⇒x=0,x≠1.
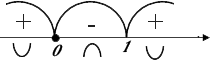
Вогнута на (-∞,0)∪(1,+∞), выпукла на (0,1).
x=0,x=1 - точки перегиба.
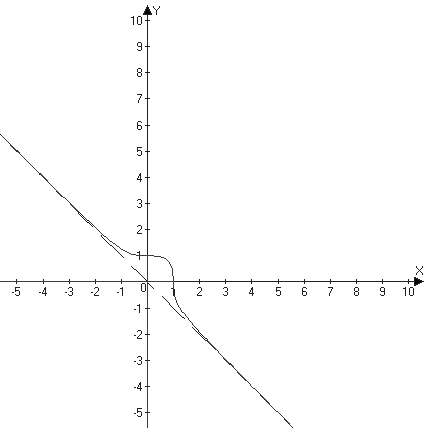

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ