Конспект урока по Алгебре "Числовые промежутки" 8 класс

Дата: 28.02

Предмет: алгебра

Класс: 8

Тема: Числовые промежутки.

Цели:

Образовательные: 1. Ввести понятие числовых промежутков и их изображение на координатной прямой;

2. ввести соответствующие обозначения;

3. рассмотреть правила изображения и записи числовых промежутков;

Развивающие: 1. развивать познавательный интерес учащихся, навыки самостоятельной работы, умение обобщать изучены материал и выбирать рациональный способ решения;
Воспитательные: 1. способствовать воспитанию внимательности, активности, дисциплинированности учащихся.

2.прививать навыки графической культуры.

Тип урока: урок изучения и первичного закрепления новых знаний.

Ход урока

Орг. момент.

- Прозвенел звонок, начинаем урок алгебры. На парте лежат: учебник, тетрадь, дневник, пенал. Садись.

Сообщение темы и цели урока (Слайд 1)

- Открываем тетрадь, записываем число, сегодня 28 февраля, классная работа, тема урока «Числовые промежутки».

- Чтобы ты хотела узнать о числовых промежутках?

+…

- Какие цели урока у нас будут?

+…..

Цели урока:

Введем понятие числовой промежуток
Рассмотреть изображение и запись числовых промежутков
Научиться строить и записывать числовые промежутки

Актуализация знаний учащихся

Задание (Слайд 2,3)

Найдите пересечение и объединение множеств А и В:

а) А ={1,5,6,7,10,12,14}, B={2,3,5,8,9,11,12}.

b) A= {А, Б, Г, Д, Е, Ж, К}, В={Б, В, Е, К, Л, М}.

с) A= {Оля, Петя, Юра, Лена, Вова}, В={Катя, Петя, Витя, Лена, Миша}.

d) А – множество отрицательных чисел, В – множество цифр.

Найдите пересечение и объединение множеств А, В, С.

А ={1,3,5,6,8,11}, B={2,5,7,11,12}, С ={1,5,6,9,11}.

Ответы (Слайд 3)

Найдите пересечение и объединение множеств А и В:

а) А∩В={5,12}, АUB={1,2,3,5,6,7,8,9,11,12,14}.

b) A∩В={Б,Е,К}, АUB = {А,Б,В,Г,Д,Е,Ж,К,Л,М}.

с) A∩В= {Петя, Лена}, АUB ={Оля, Катя, Петя, Юра, Витя, Лена, Вова, Миша}.

d) А∩В – множество отрицательных чисел, АUB – множество цифр.

Найдите пересечение и объединение множеств А, В, С.

А∩В∩С= {5,11}, АUBUС = {1,2,3,5,6, 7, 8,9,11,12}.

Изучение нового материала

(Слайд 4) Начертим координатную прямую и отметим на ней точки с координатами - 4; 3.

Если точка расположена между ними, то ей соответствует число, которое больше – 4 и меньше 3, т.е. - 4<х<3.

(Слайд 5) Множество всех чисел, удовлетворяющих условию - 4<х<3, называют числовым промежутком от – 4 до 3.

Обозначение: ( - 4; 3) Называют: ( а;b) - интервал (читают «Промежуток от –4 до 3)

(Слайд 6) Число х, удовлетворяющее условию - 4 ≤х ≤ 3, изображается точкой, которая либо лежит между точками с координатами – 4; 3, либо совпадает с одной из них.

Обозначение: [-4;3] Называют: [а;b] - числовой отрезок (читают «Промежуток от – 4 до 3, включая – 4 и 3»)

(Слайд 7)Число х, удовлетворяющее условию - 4 ≤х <3

Обозначение:[-4;3) Называют: [а;b) - полуинтервал (читают «Промежуток от – 4 до 3, включая – 4»)

(Слайд 8)Число х, удовлетворяющее условию - 4< х ≤ 3

Обозначение: (-4;3] Называют: (а;b] - полуинтервал (читают «Промежуток от – 4 до 3, включая 3»)

(Слайд 9) Отметим на координатной прямой точку с координатой 5. Если число х больше 5, то оно изображается точкой, лежащей правее этой точки.

Множество всех чисел х, удовлетворяющих условию х > 5, изображается полупрямой, расположенной вправо от точки с координатой 5.

Обозначение: (5; +∞) Называют: (а ;+∞) - открытый числовой луч (читают «Промежуток от 5 до плюс бесконечности»).

(Слайд 10) Множество всех чисел х, удовлетворяющих условию х ≥ 5, изображается той же полупрямой, включая еще точку с координатой 5.

Обозначение: [5; +∞) Называют: [а ;+∞)- числовой луч (читают «Промежуток от 5 до плюс бесконечности, включая 5»).

(Слайд 11) Множество всех чисел х, удовлетворяющих условию х <8, изображается полупрямой, расположенной левее от точки с координатой 8.

Обозначение:), Называют: (-∞ ;а) - открытый числовой луч (читают «Промежуток от минус бесконечности до 8»).

(Слайд 12) Множество всех чисел х, удовлетворяющих условию х 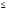8, изображается той же полупрямой, включая еще точку с координатой 8.

Обозначение:( -∞; 8]Называют: (-∞;а]- числовой луч (читают «Промежуток от минус бесконечности до 8, включая 8»).

(Слайд 13 ) Множество действительных чисел изображается всей координатной прямой.

Обозначение: .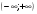

Формирование умений и навыков

(Слайд 14 ) Прочитать промежутки и дайте название:

(- 3; 5)- интервал

[- 9;12]- числовой отрезок

[- 4; 8)- полуинтервал

(-∞ ;7]- числовой луч

[6;+ ∞)- числовой луч

(-10; 13)- интервал

[- 2; 35]- числовой отрезок

[- 7; 23)- полуинтервал

(Слайд 15,16) Запишите промежутки, изображенные на рисунке.

(Слайд 17) Изобразите на координатных прямых промежутки: [2;6]и (-3;6]

- Ты справилась очень хорошо, для того чтобы углубить наши знания и познания по математике и перейти на следующий уровень, давай выполним следующее задание.

(Слайд 18) Изобразите на одной координатной прямой промежутки: [2;7]и (5;9]

Для того, чтобы не запутаться при изображение двух промежутков на координатной прямой, заштрихуем их сверху и снизу этой прямой.
При этом легко увидеть, общую часть промежутков.

- Какой промежуток служит пересечение двух данных промежутков?

[2;7]∩(5;9] = (5;7]

- Как ты думаешь какой промежуток является объединением двух промежутков?

[2;7]U(5;9] = [2;9]

(Слайд 19, 20) Изобразите на одной координатной прямой промежутки: (-7;7]и (2;10];[ 1;4]и [7;+∞]. Найдите пересечение и объединение числовых промежутков.