33

Конспект урока по теме: «Показательная функция»

Тема урока: Показательная функция

Тип урока: урок изучения нового материала

Цели урока: (представлены в таблице)

Таблица

Учебные цели

Общие категории целей

I уровень

II уровень

III уровень

1.

Знание

Ученик знает

термин “показательная функция”, формулу показательной функции; алгоритм решения простейших показательных уравнений (по графику)

Определение показательной функции, формулировки свойств показательной функции; решение простейших показательных уравнений, используя свойства показательной функции

Доказательство свойств показательной функции; обобщенные приемы исследования показательной функции.

2.

Понимание

Ученик

Узнает показательную функцию по формуле, ее график, приводит примеры показательной функции

Воспроизводит и интерпретирует свойства показательной функции при любом способе ее задания, «читает» график показательной функции, различает определение и свойство показательной функции, приводит контр. примеры.

Может записать словесно свойства показательной функции в виде формулы и, наоборот, переходит от одного языка описания функции к другому.

3.

Умения и навыки

Ученик

решает простейшие задачи: строит график показательной функции, определяет значение функции по значению аргумента по формуле и по чертежу, находит точки пересечения графиков по чертежу

Схематически строит график показательной функции, решает простейшие показательные уравнения, используя свойства функции, решает прикладные задачи в стандартных ситуациях

Решает типовые и прикладные задачи, связанные со свойствами показательной функции в измененной (нестандартной) ситуации.

Развивающие цели

1.

Сравнение

Ученик

находит общее и различное в свойствах показательной функции

сравнивает свойства показательных функций, приемы решения задач

находит общие закономерности и различные основания для сравнения показательных функций

2.

Память

запоминает и воссоздает из памяти на уровне узнавания и механически

использует сравнение для запоминания и воспроизведения

использует обобщенно-смысловое запоминание и воспроизведение

3.

Конкретизация

приводит примеры изученных показательных функций

придумывает примеры показательных функций

придумывает примеры показательных функций с заданным свойством

4.

Речь

правильно произносит термины, делает записи в тетради, задает вопросы и отвечает на них по образцу или с помощью из вне

формулирует определения и свойства, делает записи в тетрадях, свободно задает и отвечает на вопросы, используя приемы УПД

разъясняет ход решения учебной задачи с использованием специальной терминологии; внимательно слушает речь других, оценивает правильность речи.

Воспитательные цели

1.

Умение учиться

работает с учебником и решает квадратные уравнения с помощью учителя или «памяток»; ориентируясь на внешний контроль, оценку и коррекцию

работает с учебником и решает квадратные уравнения с использованием частных приемов УД, ориентируясь на взаимоконтроль

работает с учебником и решает учебные задачи самостоятельно с использованием обобщенных приемов УД, ориентируясь на самоконтроль

2.

Воспитание

интереса

проявляет интерес к отдельным (занимательным) задачам

проявляет устойчивый интерес к содержанию темы и УД

проявляет интерес к способам УД

Форма проведения урока:

Индивидуальное выполнение учебных заданий; фронтальная проверка, коррекция и формулировка выводов.

Структура урока:

1. Подготовительный этап (входной контроль, мотивация изучения нового)

2. Изучение нового материала, его осмысление и первичное закрепление.

3. Текущий контроль и проверка его результатов.

4. Подведение итогов урока и постановка домашнего задания.

Ход урока

Этап

Деятельность учителя

Деятельность учащихся

Примечания

1.

Задания теста входного контроля и ответы помещены в Приложение 2.

Дополнительные задания к ответам:

- к заданию №3: дать определение степени числа с рациональным показателем

- к заданию№4: дать определение возрастающей и убывающей функции

Один из учащихся записывает решение 2-го задания на доске, остальные сверяют свои ответы и отмечают недочеты и ошибки. Остальные задания проверяются устно (фронтально), исправляются ошибки.

Ответ:

Степенью числа а>0 с рациональным показателем r = m/n, где m

Z, n N называется число

.

Ответ: Функция f возрастает [убывает] на множестве Р, если для любых х₁, х₂ Р, таких что x₂>x₁, выполнено неравенство f(x₂)>f(x₁), [f(x₂)<f(x₁)].

Входной контроль позволяет повторить необходимый материал, определить степень подготовленности учащихся к изучению новой темы, выявить пробелы и провести коррекцию. Дополнительные задания способствуют развитию речи у учащихся

2.

После этого учитель рассказывает о процессах органического изменения величин. Рассматривает пример:

Если колония бактерий имеет достаточное пространство и достаточное количество питательных веществ, то ее масса за равные промежутки времени увеличится в одном и том же отношении. Если в начальный момент времени t = 0 значение величины равно m =1, а при t =1 m = a, при t =2 m = a², при t =3 m=a³. Какое значение примет величина в момент t=n? Но массу колонии бактерии можно наблюдать и в другие моменты времени. Чему будет равно значение массы через 3,2 единицы времени после начала наблюдения? А что обозначает запись а^-6?

Итак, какие значения может принимать t?

Для описания такого процесса, как размножение бактерий нужна функция а^х, где а>0. Так как в этой функции аргумент находится в показателе, то функцию а^х называют показательной функцией с основанием а. Учитель просит учащихся привести примеры показательных функций. Учитель разбивает класс на две команды: одна строит график функции у=2^х (по точкам), другая у=(1/2)^х и исследуют данные функции по следующему плану:

1) область определения

2) область значений;

3) промежутки возрастания или убывания;

4) точки пересечения с осями координат.

Учитель просит сравнить эти функции и выявить, что у них общего.

Ответ:

При t=n m=aⁿ

Ответ: t=3,2 m=a^3,2

Ответ: значение массы в момент времени t =-6 (т.е. за 6 единиц времени до начала наблюдения).

Ответ t может быть целым, дробным, иррациональным, положительным, нулевым и отрицательным.

Записывают определение: функция, заданная формулой у= а^х, где a>0, называется показательной функцией с основанием а.

Приводят примеры показательных функций.

Один из представителей первой команды составляет таблицу на доске и чертит график функции по точкам.

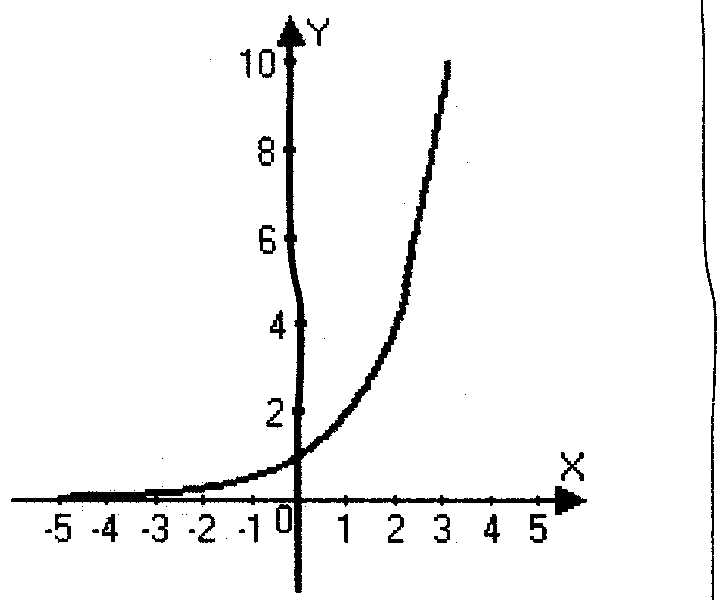
Другой представитель этой же команды исследует данную функцию.

Свойства:

1) D(y)=R

2) E(y)=(0; )

3) возрастает на R

4) (0,1) – точка пересечения с осью OY.

Представитель другой команды строит график функции у=(1/2)^х

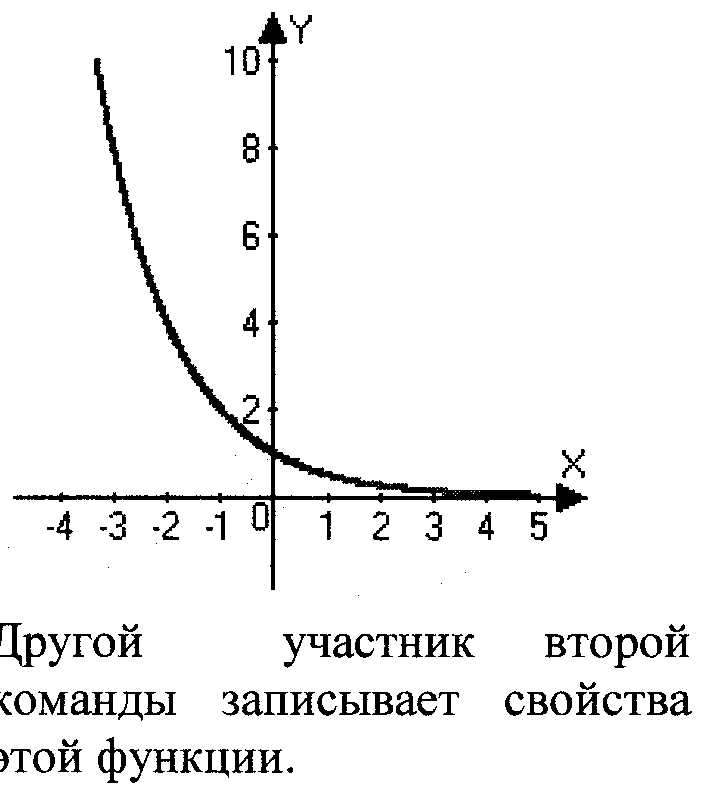
Свойства:

1) D(y)=R

2) E(y)=(0; )

3) убывает на R

4) (0,1) – точка пересечения с осью OY.

Сначала учащиеся обсуждают в слух, а затем записывают в тетрадь свойства показательной функции:

1) D(y)=R

2) E(y)=(0; )

3) при a>1 функция возрастает на множестве R, а при 0<a<1 функция убывает на множестве R.

На данном этапе происходит мотивация изучения нового материала, показана ситуация применения показательной функции (связь с жизнью)

Мотивировка термина, означающего данное понятие. Это задание способствует развитию такой категории мышления как коекретизация.

На данном этапе учащиеся пытаются установить сходство и различие показательных функций с различными основаниями и на основе этого формулируют свойства показательной функции, что способствует развитию таких качеств мышления как сравнение, синтез, обобщение

3.

Учитель предлагает выполнить следующие задания:

1) Постройте график функции у=3^х и по графику найдите

а) значение у, соответствующие значению х, равному -1; 0; 0,5; 1.

б) при каокм значении х значение у равно 1; 3; 6.

2) Постройте график функции у=0,7^х. С помощью графика сравните выражения

0,7^3,2 и 0,7^-1,7;

0,7^1,5 и 0,7⁵;

0,7^0,5 и 0,7^2,3

3) Решите устно уравнения:

а) 5^х=1/5

б) 7^х=49

Задания теста для текущего контроля и ответ помещены в приложении 3.

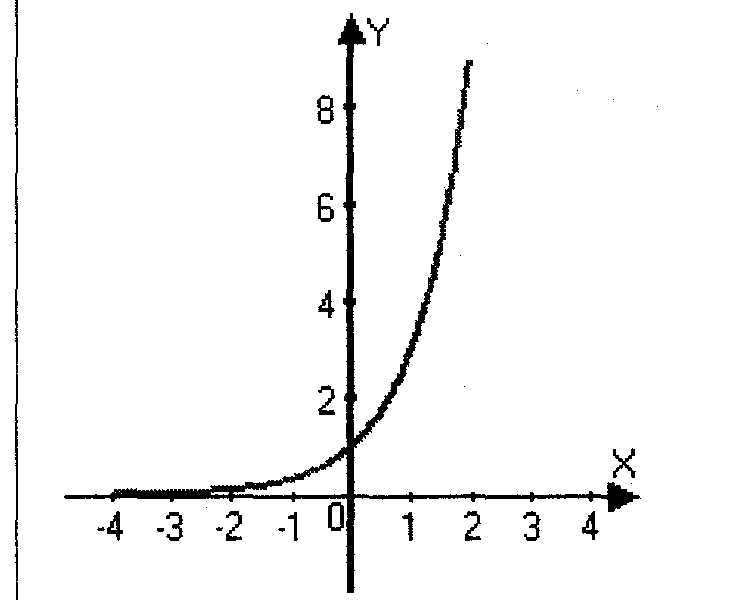
Один из учеников выполняет на доске, остальные в тетрадях.

Ответы:

а) х=-1 у=1/3

х=0 у=1

х=0,5 у=1,7

х=1 у=3

б) у=1 х=0

у=3 х=1

у=6 х=1,6

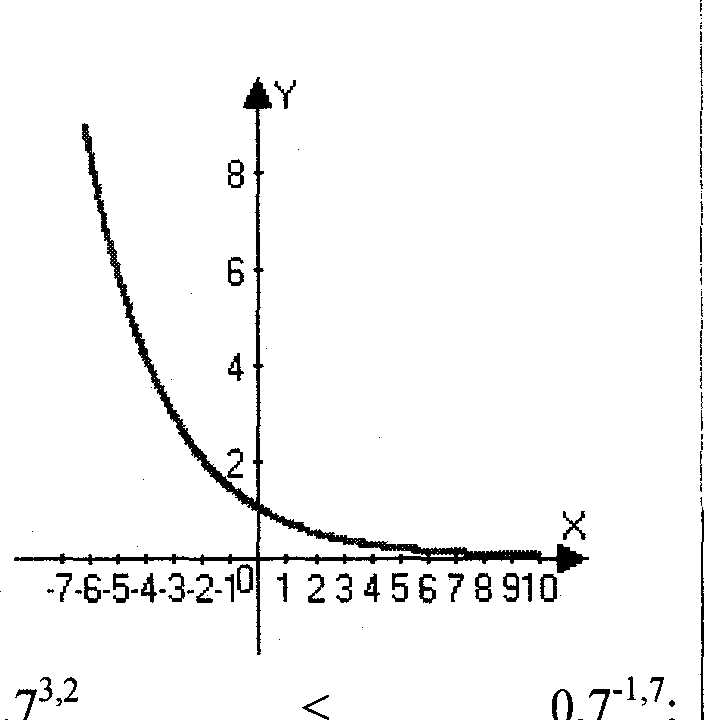0,7^3,2 < 0,7^-1,7;

0,7^1,5 > 0,7⁵;

0,7^0,5 > 0,7^2,3

х=-1

х=2

Решение типовых задач в сходных ситуациях, происходит закрепление изученного материала

Способ проверки результатов – взаимопроверка в парах с ориентацией на правильные ответы. Подведение итогов выполнения теста, выявление ошибок, общая оценка результатов выполнения в совместном обсуждении

4.

Домашнее задание включает: а) изучение основного материала по учебнику и записям в тетрадях; б) № 200 (3,4), № 201 (1,2) (уч. Алимова), в) найти области применения показательной функции, доказать ее основные свойства (для желающих).

Записывают задания в дневник, задают вопросы по заданию

Последнее задание ориентировано на учащихся с повышенным интересом к математике (III уровень)

Тест на тему: Показательная функция.

1. обведите кружком варианты ответа да если вы согласны с утверждением, если не согласны обведите нет.

Задание.

1. ДА НЕТ

2. = x1 – x2 ДА НЕТ

3. () = ДА НЕТ

2.Обведите кружком номер правильного ответа.

Задание: Решите показательное уравнение.

Ответы:

А. 5 Б. 4 В. 3 Г. 2

3. Каждому элементу первого столбца поставьте в соответствие элемент из второго столбца.

1столбец 2 столбец

Вид уравнения, неравенства Уравнение, неравенство

1. Иррациональное уравнение A. 6x -45 = 23

2. Показательное уравнение B.

3.Показательное неравенство С.

4. Линейное уравнения D.

4. Обведите кружком номер правильного ответа.

Укажите промежуток, который является ответом данного неравенства

1.(-∞;+∞) 2. (-∞;3) 3. (-3;3) 4. (3;+∞)

5. Обведите кружком номера правильных ответов.

Среди функций, заданных формулами укажите те, которые являются возрастающими:

1. 2. 3. 4.

6. Обведите кружком номер правильного ответа.

Найдите корень показательного уравнения.

1. 6 2. 3 3. 7 4. 2

7. Обведите кружком номер правильного ответа.

Решите показательное уравнение

A.5 B.4 C.1 D.0

8. Обведите кружком номер правильного ответа.

Укажите наибольшее из корней данного уравнения

1. 0 2. 6 3. 4 4. 2

9. Обведите кружком номер правильного ответа.

Чему будет равно произведение x*y.

1. -2 2. -3 3. 0 4. 4

10. Обведите кружком номер правильного ответа.

Найдите минимальное целое х.

1. 18 2. 16 3. 14 4. 12