Конспект урока алгебры и начала анализа в 11 классе

по теме: «Тригонометрические уравнения (урок обобщения и систематизации знаний)»

учителя математики МОУ СОШ № 2 г. Питкяранта РК

Никитиной С.В.

Тип урока: Урок обобщения и систематизации.

Методы:

- частично-поисковый;

- поисковый;

- проблемный;

-исследовательский – решение познавательных обобщающих задач;

- системные обобщения;

- самопроверка;

- самооценка.

Использованные технологии: технология сотрудничества – работа в малых группах, когда успех всех зависит от успеха каждого; информационная технология – использование возможностей компьютера.

Цель урока: Обобщить и систематизировать знания по теме «Тригонометрические уравнения», продолжить работу по подготовке к ЕГЭ.

Ход урока:

1°. Орг. момент

2°. Разминка

3°. Повторение.

4°. Решение простейших тригонометрических выражений. Индивидуальные задания.

5°. Работа в группах.

6°. Индивидуально-дифференцированная работа.

7°. Итог урока.

8. Задание на дом.

Формы организации труда:

- индивидуальная;

- фронтальная;

- групповая;

- индивидуально-дифференцированная.

1°. Орг. момент.

Сегодня на уроке мы обобщаем и систематизируем полученные знания по теме «Тригонометрические уравнения», напоминая основные и специальные методы их решения, повторяя формулы и приёмы и тем самым – продолжаем подготовку к ЕГЭ

Девизом урока предлагаю слова Сухомлинского, зашифрованные в ребусе. Для этого надо решить устные упражнения и по ответам находить слова этого крылатого выражения:

1) sin (π+ x)

2) arccos (-x)

3) sin x = 0

4) 2 cos x = 1

5) 5sin²x-7+5cos²x

6) arctg 1

7) cos x = a

8) ctg x = a

9) x² + 5x +6 =0

10)sin π/4 +cos π/2

11) sin (-x)

12)arcsin(-/2)

13)y = cos(x-π)

14)arcctg(-1)

15) arccos (- 1/2)

16) sin (3π/2 – x)

17) ctg(- x)

18)arcsin(-1)+arccos1

19) sin x = a

20) tg x = a.

21) tg π/4

22) 7²

23) sin²x+ tgxctg x +cos²x

24)

X =

У Ч И Т Е Л Ь

Б У Д У Щ Е М

-2 и 3

В Ы

– sin x

С Е Г О Д Н Я

–

У Ч И Т Е Л Я,

В

X = arcctg a + πn, n ЄZ

И

X= arctg a + πn,nЄZ

В

π– arccos x

М Ы

2

П Р О Г Р Е С С А

-

Н О

X= (- 1)ⁿarcsin a +πn, n Є Z

И Н А Ч Е

X=πn, nЄZ

У Ч И М С Я

У Ч Е Н И К

X=

В М Е С Т Е

2

Б У Д Е Т

М О И

49

НЕ

– cos x

Д О Л Ж Е Н

– 2

Я

2

Н А У К Е

– sin x

У Ч Е Н И К И.

– ctg x

П Р Е В З О Й Т И

ВАШ

На плакате появляется эпиграф урока: “Сегодня – мы учимся вместе: я, ваш учитель и вы мои ученики. Но в будущем ученик должен превзойти учителя, иначе в науке не будет прогресса ”. (Сухомлинский)

На доске записаны уравнения. Исходя, из записей на доске определите тему нашего урока.

« Решение тригонометрических уравнений»

Верно, подготовка к ЕГЭ.

Давайте подумаем, что мы должны хорошо знать, для того, чтобы решить тригонометрическое уравнение.

Выслушиваются ответы учащихся (формулы по тригонометрии, решение простейших тригонометрических уравнений, способы решения уравнений и т.д.)

Слабым учащимся дается задание заполнить таблицу в парах

Задание: заполнить 3 столбец таблицы

Значения

а

Уравнение

Формулы решения уравнений

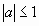
sinx=a

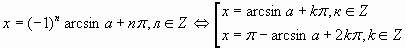
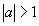
sinx=a

уравнение решений не имеет

а=0

sinx=0

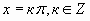
а=1

sinx= 1

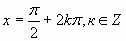
а= -1

sinx= -1

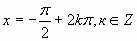
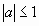
cosx=a

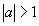
cosx=a

уравнение решений не имеет

а=0

cosx=0

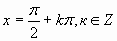
а=1

cosx= 1

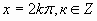
а= -1

cosx= -1

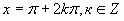
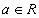
tgx=a

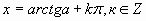
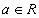
ctgx=a

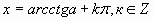
Для остальных:

2°. Разминка. Диктант «Верно - неверно» (самопроверка)

3.Три слабых ученика к доске - решить простейшие уравнения (тем, кто записывал формулы)

А1

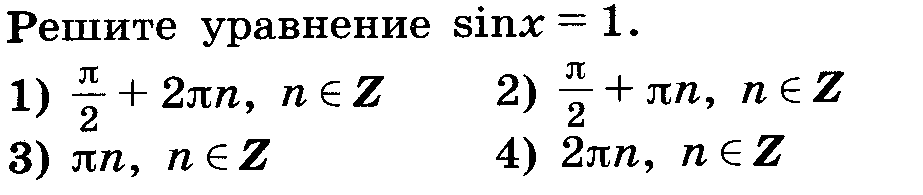
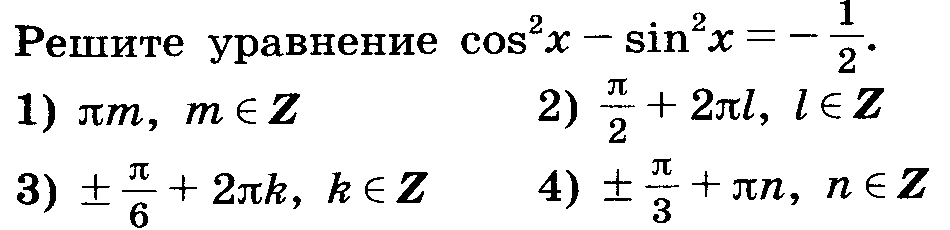
А3

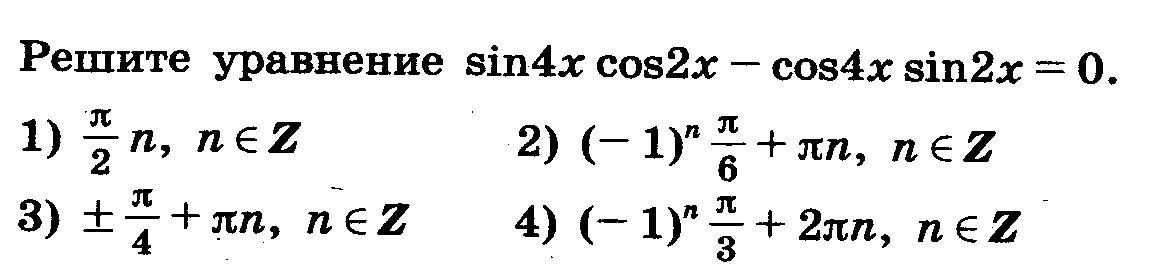
А 4

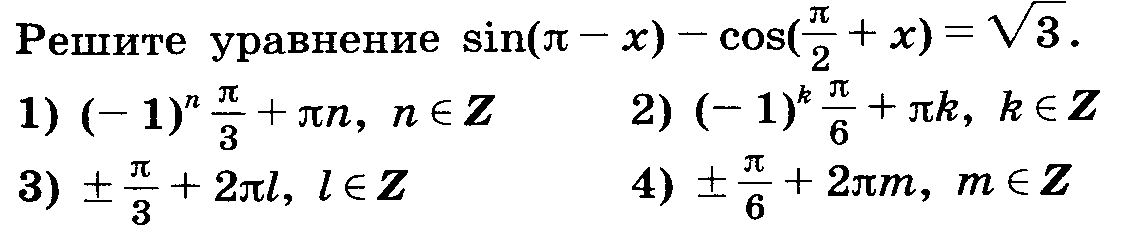
Проверяют сильные ученики

4.Классу задания: на доске записаны уравнения, разделите их на группы по способам решения

3 sin²x + cos²x = 1 - sinx cosx

4 соs²x - cosx – 1 = 0

2 sin² ^x/₂ + cosx = 1

cosx + cos3x = 0

2 sinx cos5x – cos5x = 0

2sinxcosx – sinx = 0

3 cos²x - cos2x = 1

6 sin²x + 4 sinx cosx = 1

4 sin²x + 11sinx = 3

sin3x = sin17x

А для этого надо вспомнить методы решения тригонометрических уравнений, которые мы знаем

Обсудите в парах, какие способы вам известны.

Учащиеся вспоминают и называют способы. Затем показывается слайд с методами решения.

После этого учащимся дается задание по вариантам (для проверки поменялись тетрадями вариант со своим вариантом)

Вариант I

Предложите способ решения данного тригонометрического уравнения:

1)приведение к квадратному;

2)приведение к однородному;

3)разложение на множители;

4)понижение степени;

5)преобразование суммы тригонометрических функций в произведение.

Уравнение

Способы решения

1

2

3

4

5

а)3 sin²x + cos²x = 1 - sinx cosx

б)4 соs²x - cosx – 1 = 0

в)2 sin² ^x/₂ + cosx = 1

г) cosx + cos3x = 0

д)2 sinx cos5x – cos5x = 0

Вариант II

Предложите способ решения данного тригонометрического уравнения:

1)приведение к квадратному;

2)приведение к однородному;

3)разложение на множители;

4)понижение степени;

5)преобразование суммы тригонометрических функций в произведение.

Уравнение

Способы решения

1

2

3

4

5

а)2sinxcosx – sinx = 0

б)3 cos²x - cos2x = 1

в)6 sin²x + 4 sinx cosx = 1

г)4 sin²x + 11sinx = 3

д) sin3x = sin17x

5.Физминутка

Задание для снятия утомляемости глаз: нельзя водить руками, а лишь только глазами В таблице расположены числа от 1 до 20, но четыре числа пропущены. Ваша задача: назвать эти числа.

5

13

18

3

19

1

8

16

12

14

20

10

4

9

15

6

6.Дома было дано задание, придумать как можно больше способов решения уравнения

К доске выходят три ученика и записывают по 2 различных способа (объясняют)

7.Учащимся предлагается выполнить задание С1:

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие промежутку .

Решение.

а) (один ученик у доски):
Так как (формула косинуса двойного угла), (формула приведения), то , , (вынесение за скобки общего множителя).

Корни уравнения: , .

б) Работа по группам:

1 группа. Отбор корней по единичной окружности.

Корни уравнения изображаются точками А и В, а корни уравнения - точками C и D, промежуток изображен жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: и .



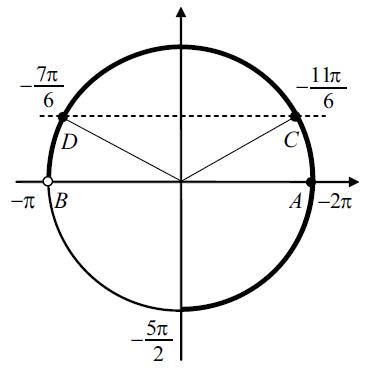
б)Ответ: .

2 группа. Отбор корней по графику.

б) Корни, принадлежащие промежутку, отберем по графику. Прямая (ось ) пересекает график в единственной точке, абсцисса которой принадлежит промежутку.

Прямая пересекает график ровно в двух точках, абсциссы которых принадлежат(см. рис.). Так как период функции равен , то эти абсциссы равны, соответственно, и .



В промежуткесодержатся три корня: .

3 группа. Отбор корней перебором значений.

б) Пусть . Подставляя , получаем . Промежутку принадлежит только .

Пусть . Подставляя , получаем:

.

Промежутку принадлежат только .

Промежутку принадлежат корни: .

4 группа. Отбор корней аналитически с помощью неравенств.

б) Отберем корни, принадлежащие промежутку.

Пусть .. Тогда .

Корень, принадлежащий промежутку: .

ПустьZ.

Тогда.

Корень, принадлежащий промежутку: .

ПустьZ.

Тогда.

Корень, принадлежащий промежутку: .

Промежутку принадлежат корни: .

8. Работа в группах.

Каждой группе предложено несколько уравнений. Необходимо, если возможно, определить вид уравнений и метод, который будет использоваться в решении этих уравнений. Решить уравнения и одно - два из них (по выбору группы) записать на доске и прокомментировать решение.

1 группа Уравнения, решаемые алгебраическими методами (методом разложения на множители, методом введения новой переменной). Выбрать корни принадлежащие промежутку [п/2; 2п] в 1 и 2 уравнениях

2 группа Однородные уравнения и сводимые к ним. Выбрать корни принадлежащие промежутку [п/2; 2п] в 1 и 2 уравнениях

3 группа Неоднородные уравнения. Выбрать корни принадлежащие промежутку [ п/2; 2п] в 1 и 2 уравнениях

4 группа Уравнения, решаемые при помощи преобразований, на основе формул преобразования сумм в произведение, произведения в сумму, понижения степени. Выбрать корни принадлежащие промежутку [п/2; 2п] в 1 и 2 уравнениях

9. Решение уравнений

Индивидуально-дифференцированная работа. Дети выбирают сами. Сколько успеют, остальное по выбору решают дома.

На “3”. Решите уравнения: 1) sinx =

2) cos² x – 9 cos x + 8 = 0

3)

На “4”. Решите уравнение:

1) cos ²x – 9cos x +8=0

2) sin 2x sin 3x=0

3) cos x + sin x = 0

4) (cos x – 1)

На “ 5”. Решите уравнение:

1) 2cos²x + 3sin x = 0

2) 3 sin x cos x – cos² x = 0

3) Найдите среднее арифметическое корней уравнения

cos² x + sin x cos x = 1 на промежутке [-π;π]

4)

5) 3 – 4 sin² (3x+

6) | cos | = 2cos x –sin x.

10.Итог урока.

По окончании урока каждый ученик сам себя оценивает, отмечает это в листе учета. Подводятся итоги урока, анализируется работа каждого ученика.

Ф.И учащегося____________________________________________________________

№

Название этапа

Количество верных шагов

Оценка

Оценка

1

• Девиз

2

• Разминка (верно – неверно)

 

 

 

3

• Повторение. (Выбор способа решения уравнения)

 

 

 

4

 

• Индивидуальное задание

 

 

 

5

• Работа в группах.

 

 

 

6

 

• Индивидуально-дифференцированная работа.

 

 

 

8. Домашняя работа индивидуально-дифференцированная, причем каждому ученику есть возможность “ продвинуться”, те кто решал на “3” дома будет решать на “4”, кто на “4”,тот на “5”,а кто на “5”, тот на “5/5”.

Предлагаю закончить урок словами Я.А.Коменского: “ Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию ”.