Тест по теме «Показательная функция» 10-11 класс
Тест по теме «Показательная функция»
Составлен учителем математики КГУ «Школа-лицей «Дарын»
Величко Оксаной Николаевной
на основе учебника
«Алгебра и начала математического анализа 10-11классы» Мордкович А.Г..
Пояснительная записка.
Задания данного теста соответствуют теории по теме «Показательная функция» в пределах учебного материала для выпускников 11 класса. Они предназначены для проверки уровня знаний, умений и навыков учащихся по данной теме. При решении заданий этого теста необходимо хорошо знать и уметь применять на практике определения и свойства показательной функции, иметь навыки решения показательных уравнений и неравенств.
В тесте представлены два варианта, в каждом из которых пятнадцать заданий и ответы к ним.
Вариант 1.
Тест по теме «Показательная функция»
Из приведенных ниже функций укажите показательную:
а) у=х3 б) ![]() в)
в) ![]() г)
г) ![]()
1) а и в
2) а и б
3) в и г
4) б и г
Из приведенных ниже утверждений верными являются:
а) функция ![]() принимает в некоторой точке значение 0;
принимает в некоторой точке значение 0;
б) функция ![]() является нечетной;
является нечетной;
в) функция ![]() пересекает ось Оу в точке (0; 1);
пересекает ось Оу в точке (0; 1);
г) функция ![]() принимает только положительные значения.
принимает только положительные значения.
1) а и в
2) а и б
3) в и г
4) б и г
При каких значениях х выражении
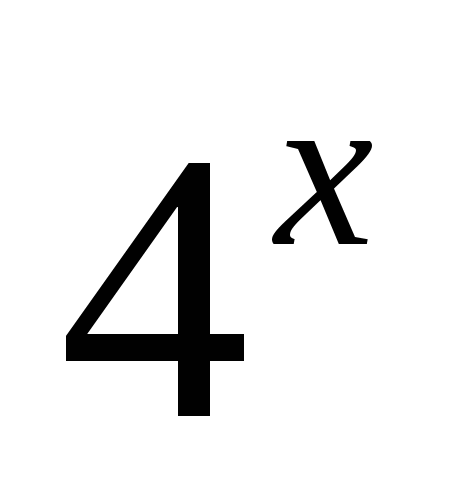 больше 1?
больше 1?1) x>0
2) x<0
3) x>1
4) x<1
Областью значений функции
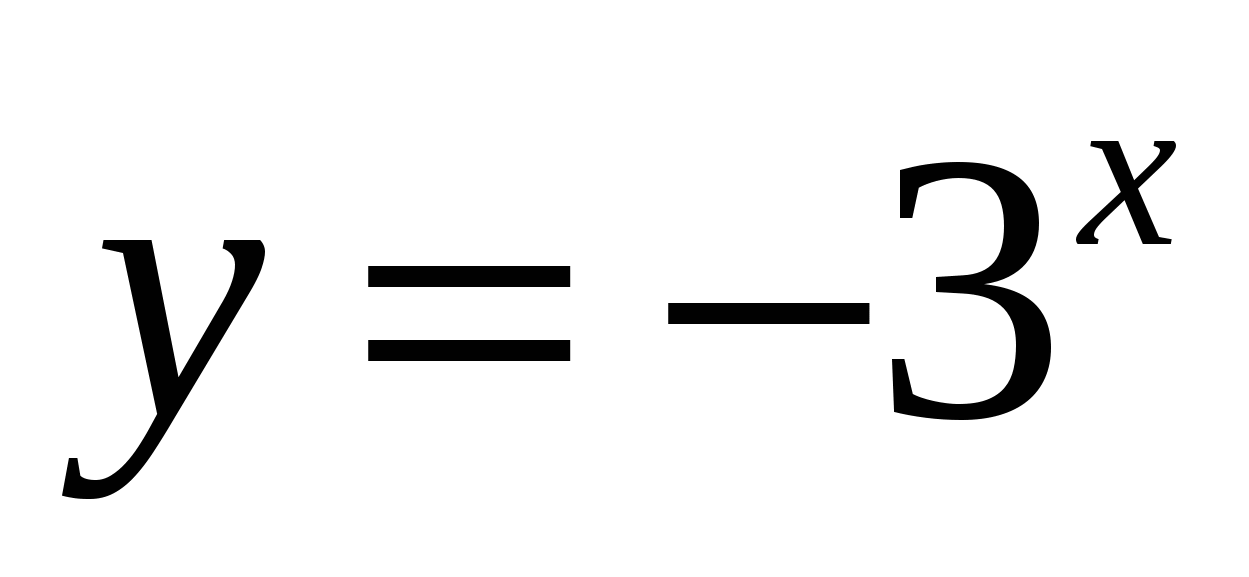 является множество
является множество1)
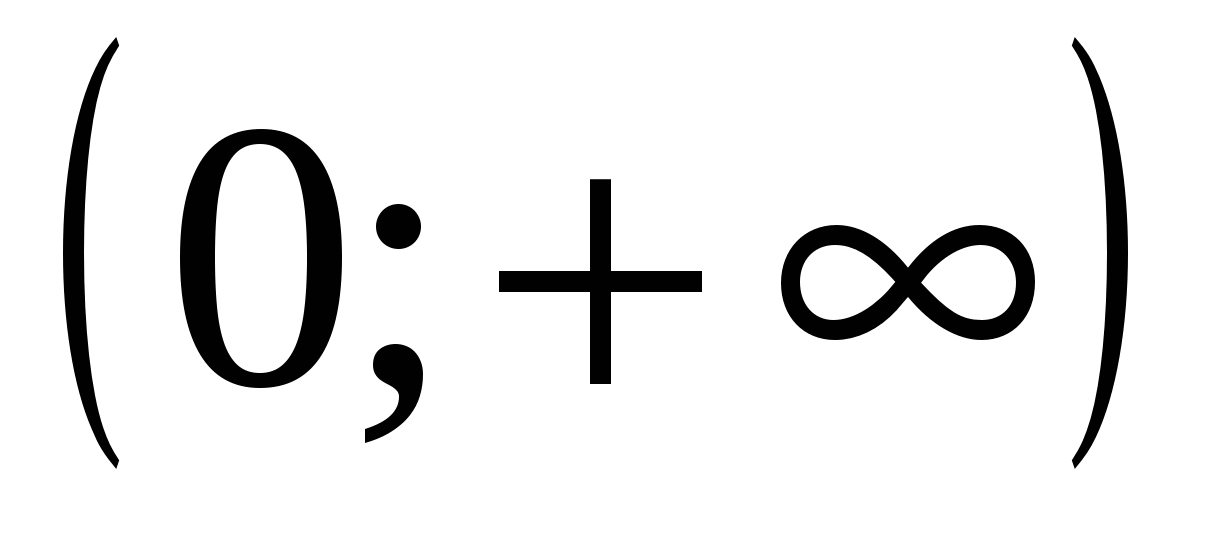
2)
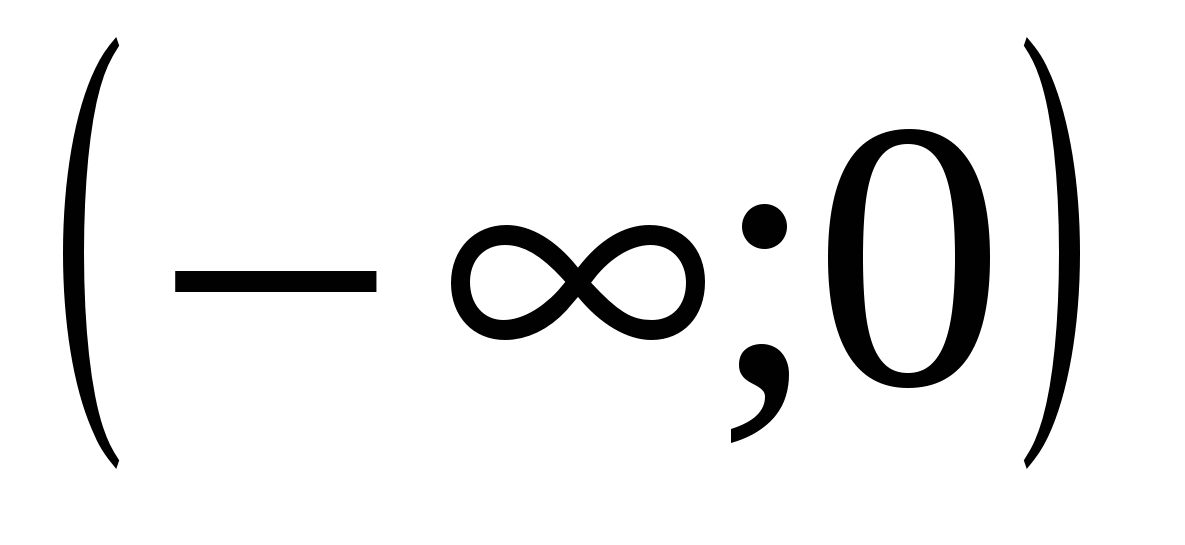
3)
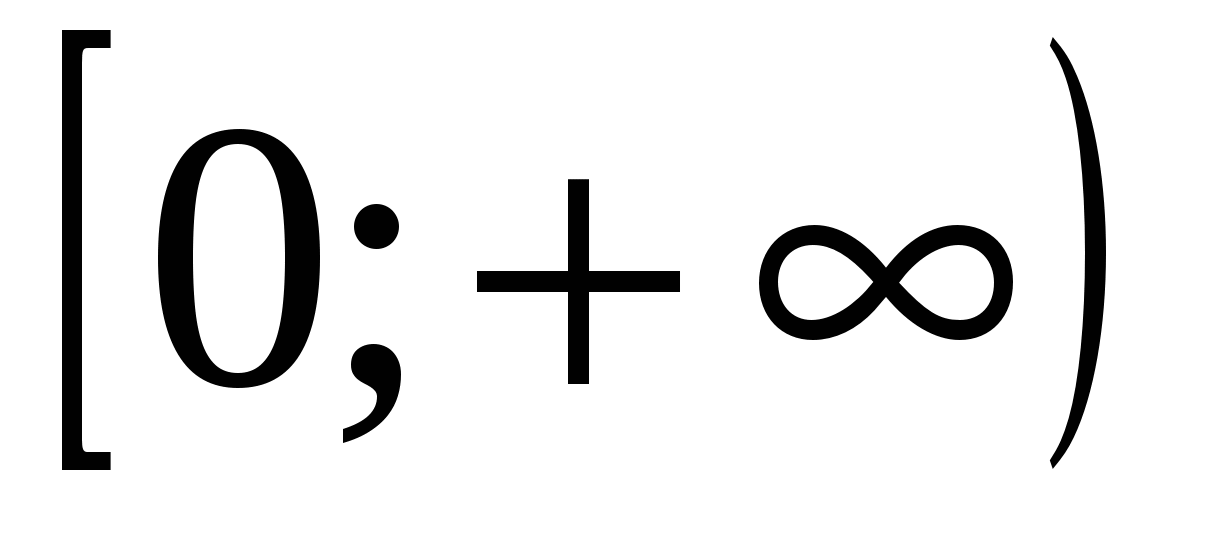
4)
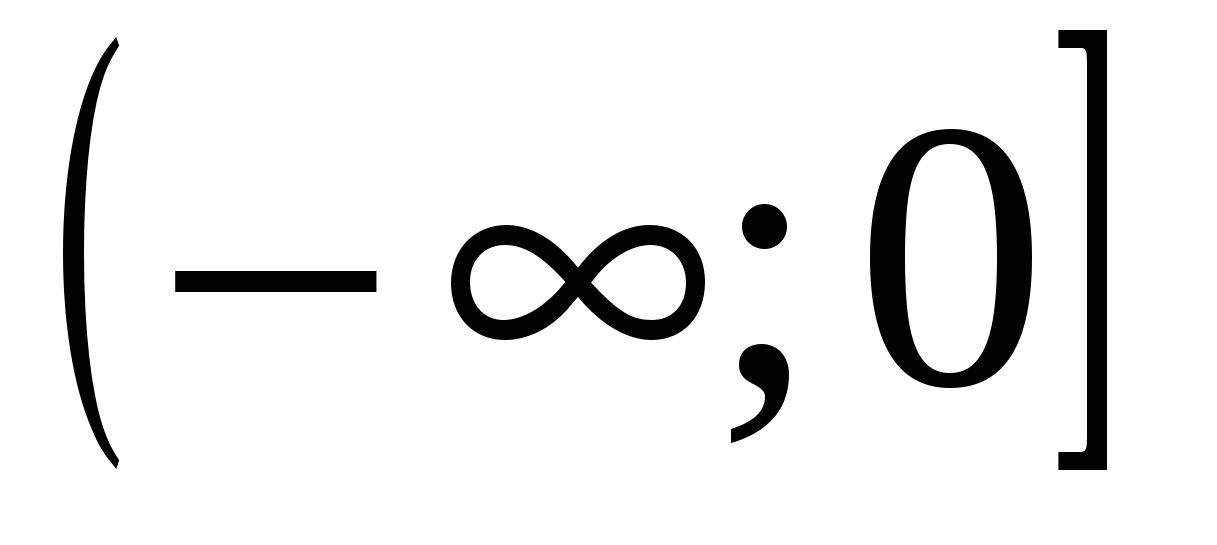
Из приведенных ниже утверждений верными являются:
а) графики функций ![]() и
и ![]() симметричны относительно оси ординат;
симметричны относительно оси ординат;
б) графики функций ![]() и
и ![]() пересекают ось Оу в точке (0; 1);
пересекают ось Оу в точке (0; 1);
в) графики функций ![]() и
и ![]() симметричны относительно оси абсцисс;
симметричны относительно оси абсцисс;
г) графики функций ![]() и
и ![]() пересекают ось Ох в точке (1; 0).
пересекают ось Ох в точке (1; 0).
1) а и в
2) а и б
3) в и г
4) б и г
Из приведенных ниже функций укажите возрастающие:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
1) а и в
2) а и б
3) в и г
4) б и г
Корень уравнения
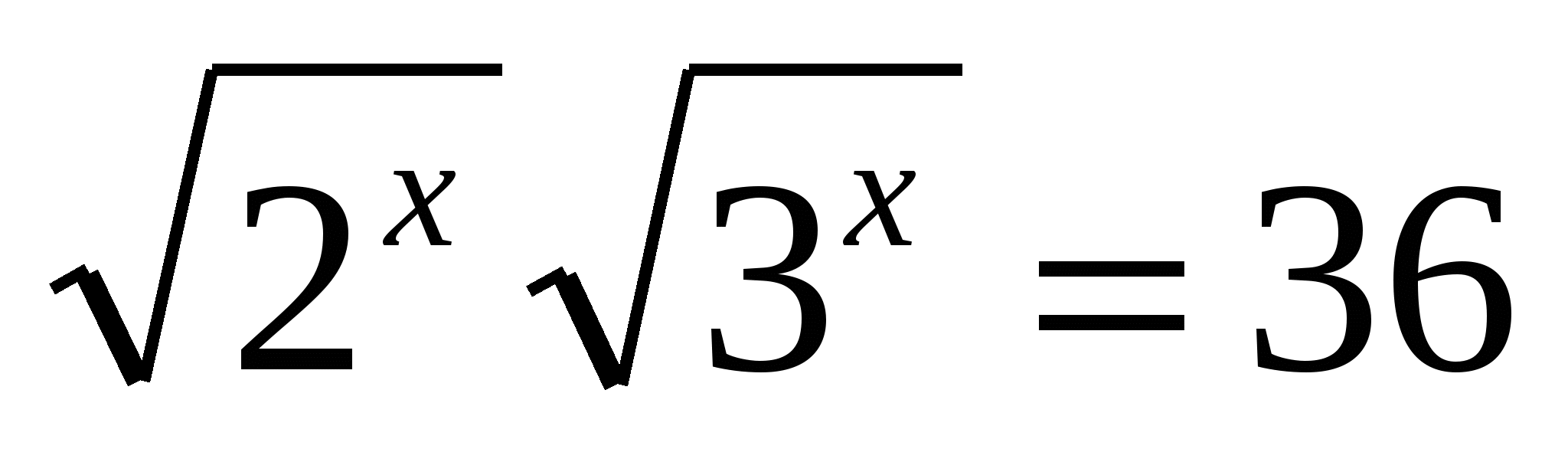 равен
равен
1) 1
2) 2
3) 3
4) 4
Выражение 2а, где а - корень уравнения
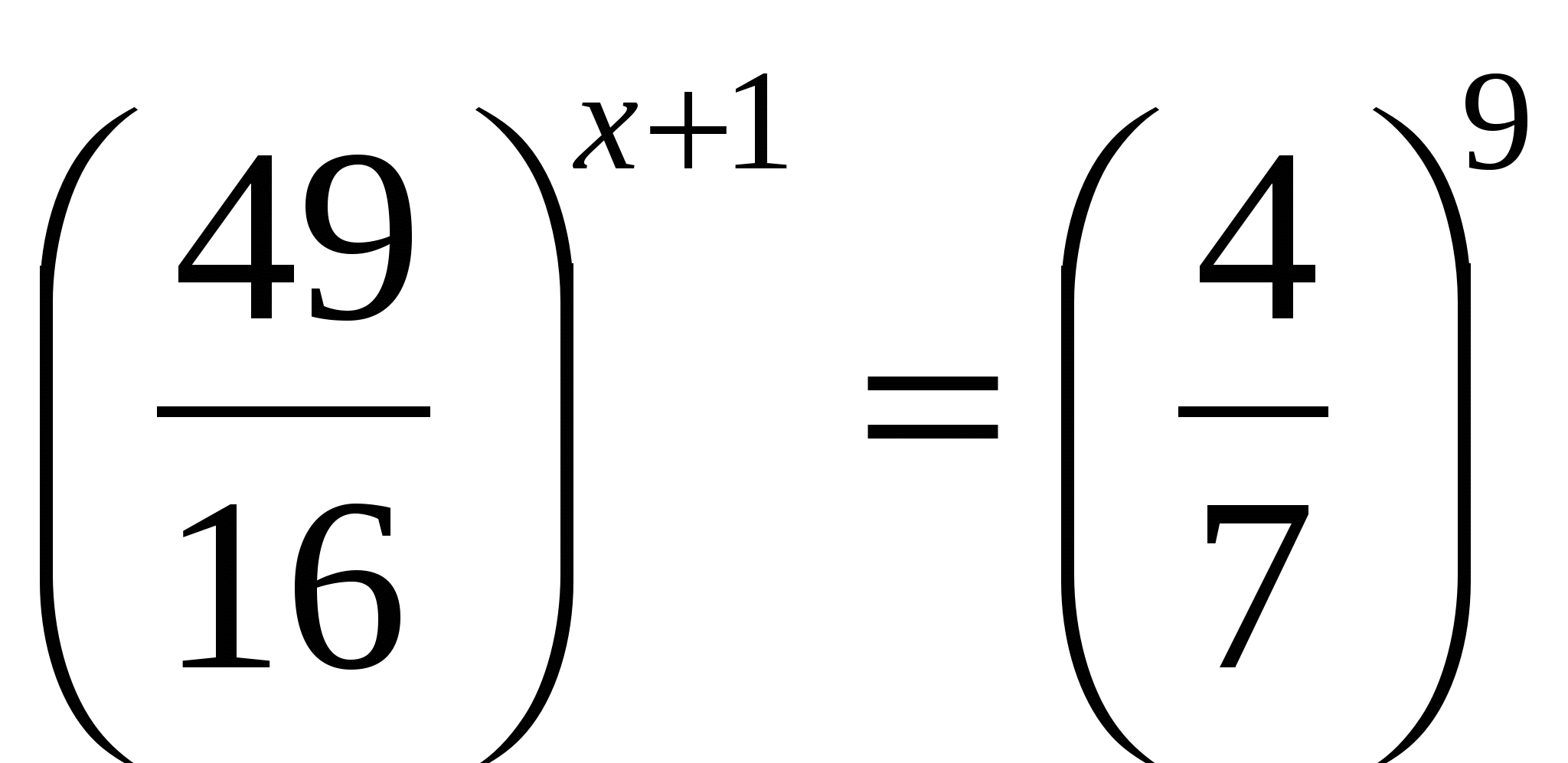 , равно
, равно1) 9
2) 11
3) -11
4) -9
Произведение корней уравнения
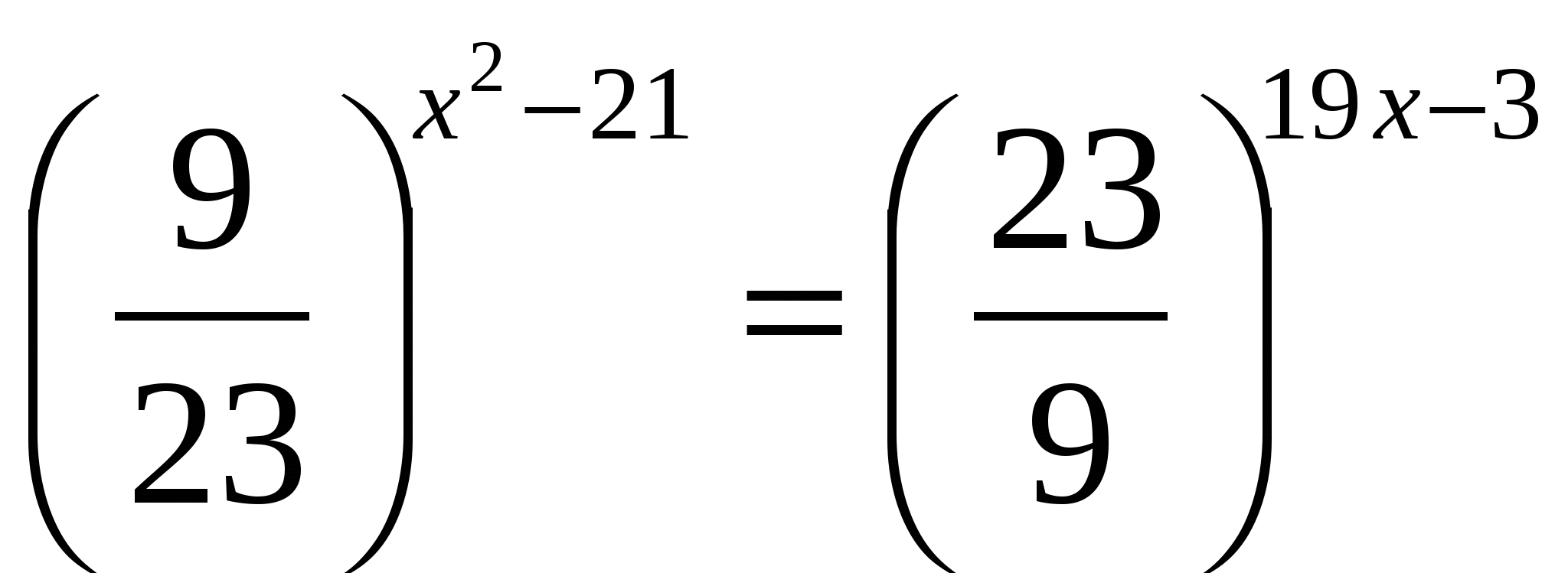 равно
равно1) 19
2) -19
3) -24
4) -18
Выражение 0,2+а, где а - корень уравнения
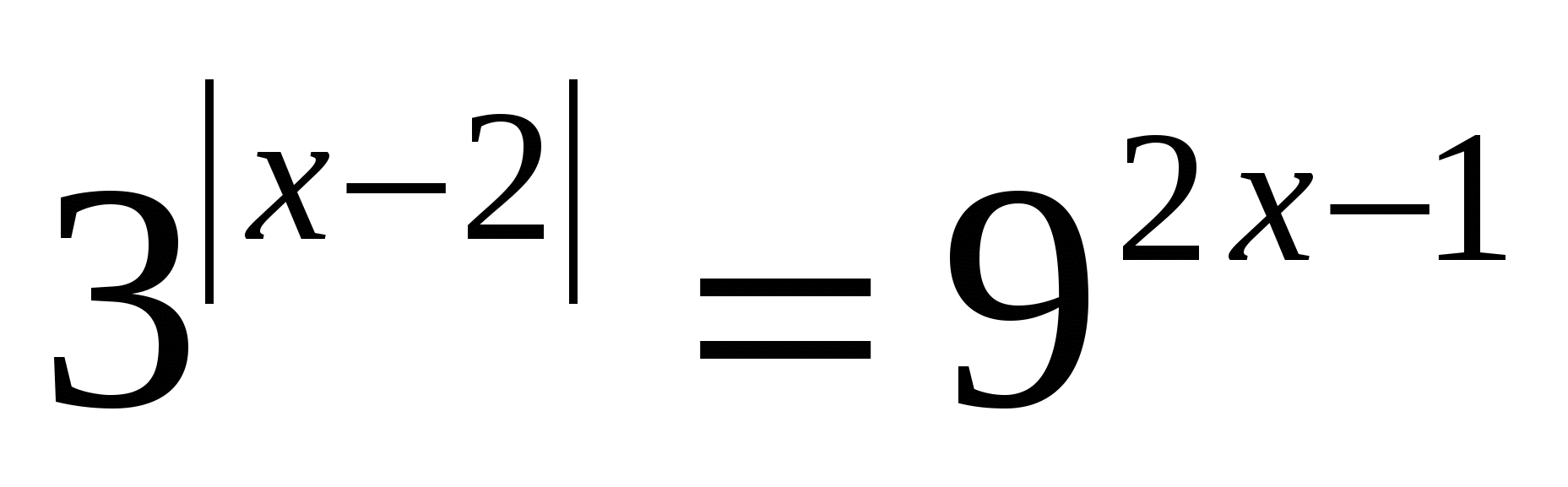 равно
равно1) 1
2) 0,2
3) -1
4) -0,2
Решением неравенства
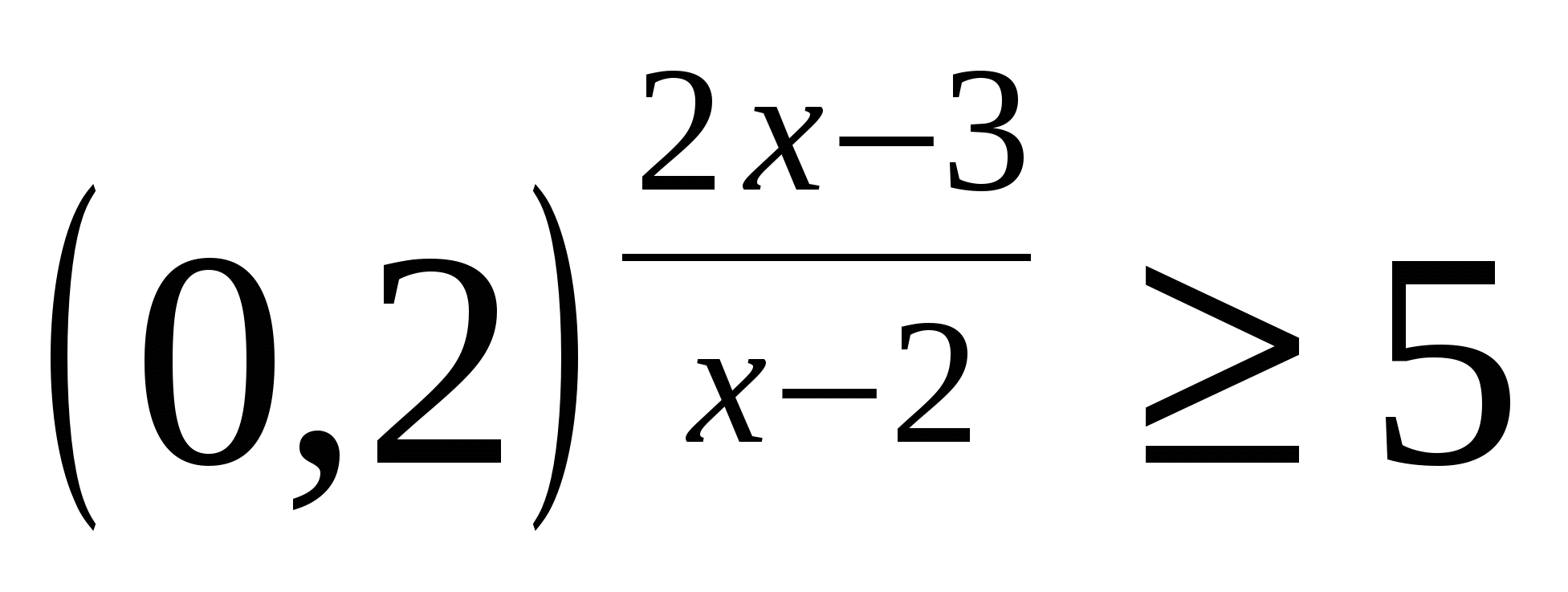 является множество
является множество1)
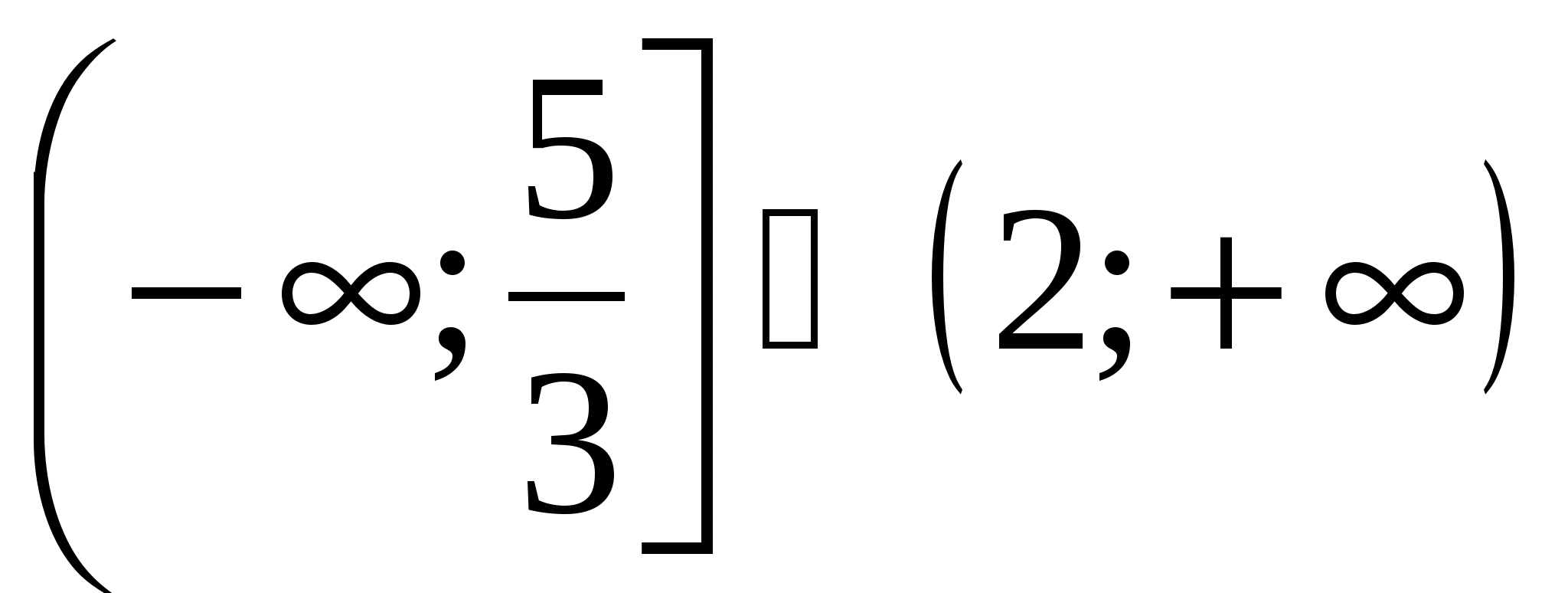
2)
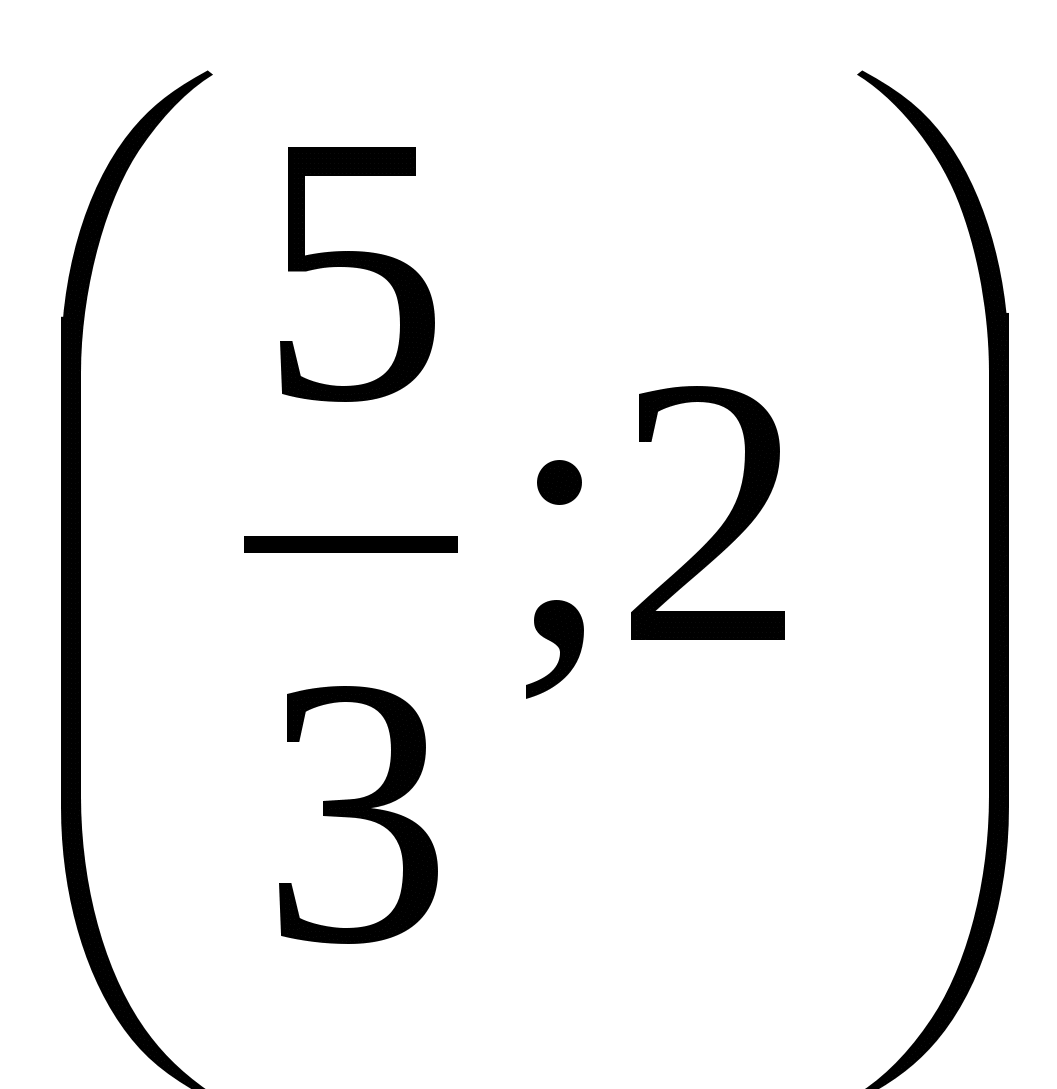
3)
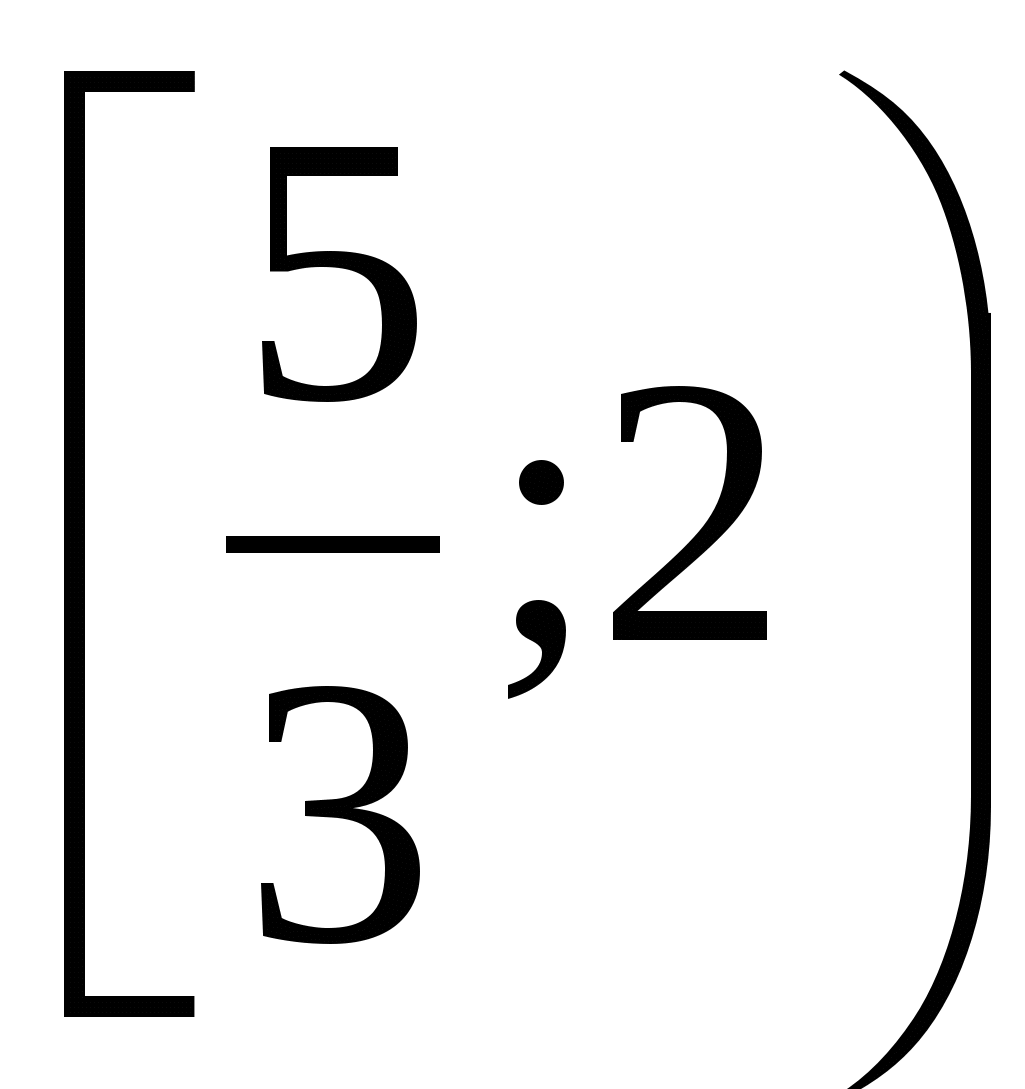
4)
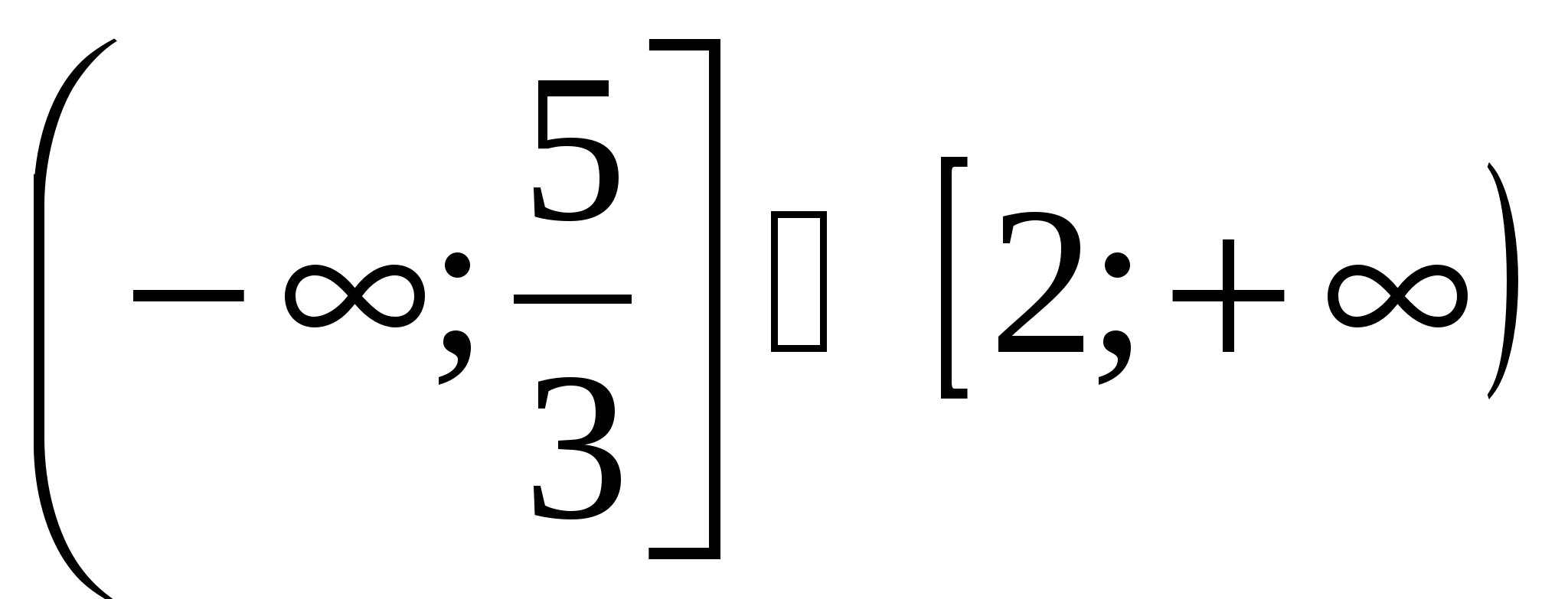
Решением неравенства
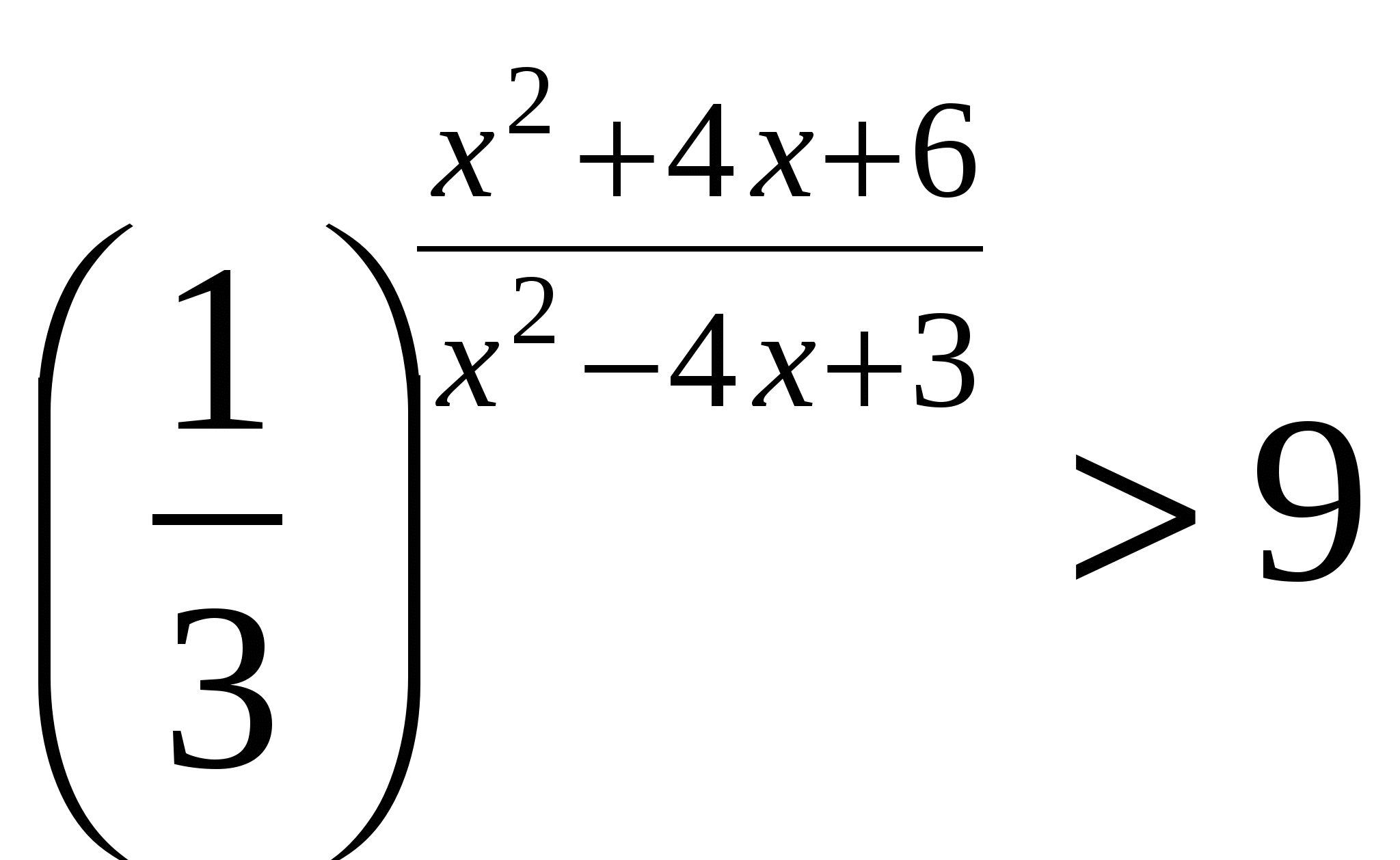 является множество
является множество 1)
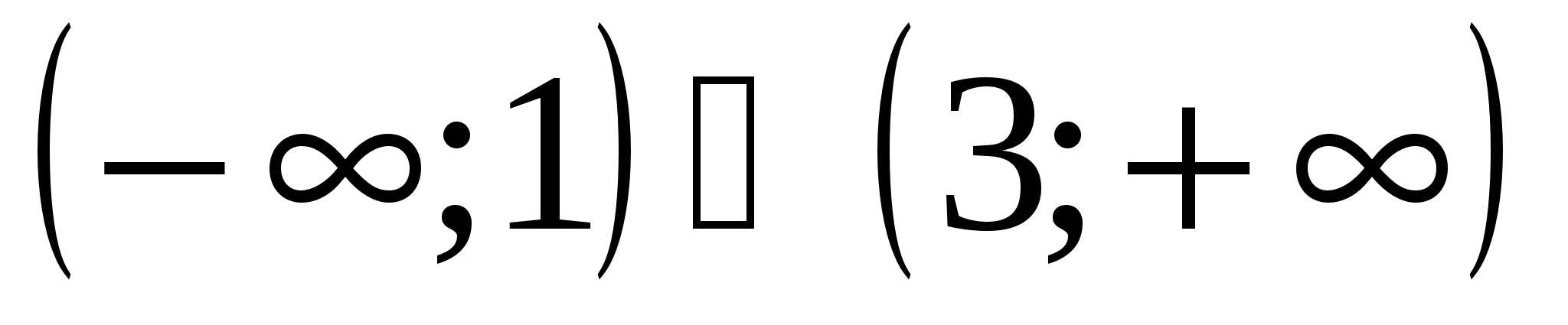
2)
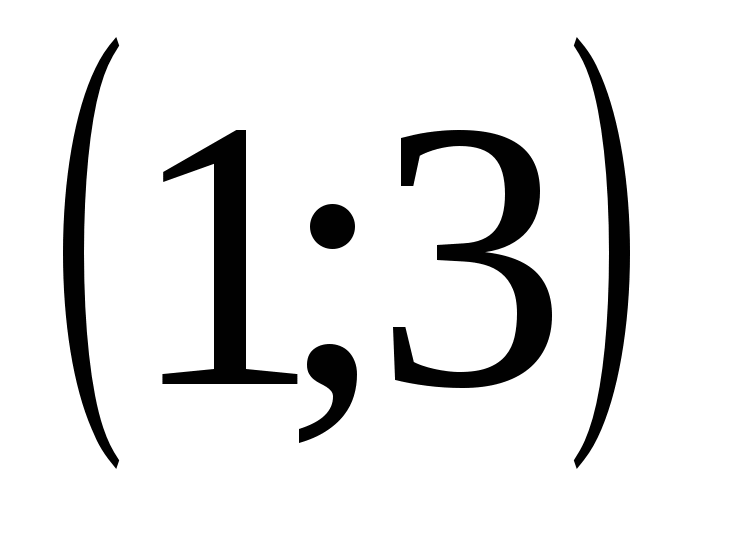
3)
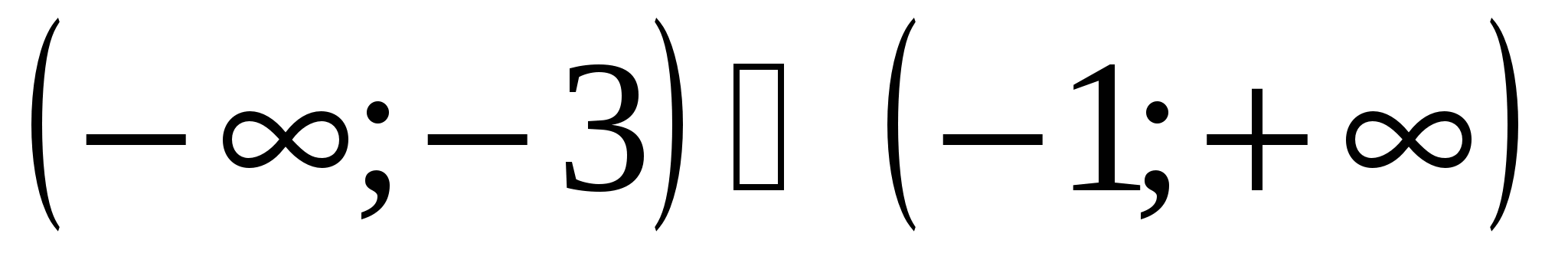
4)
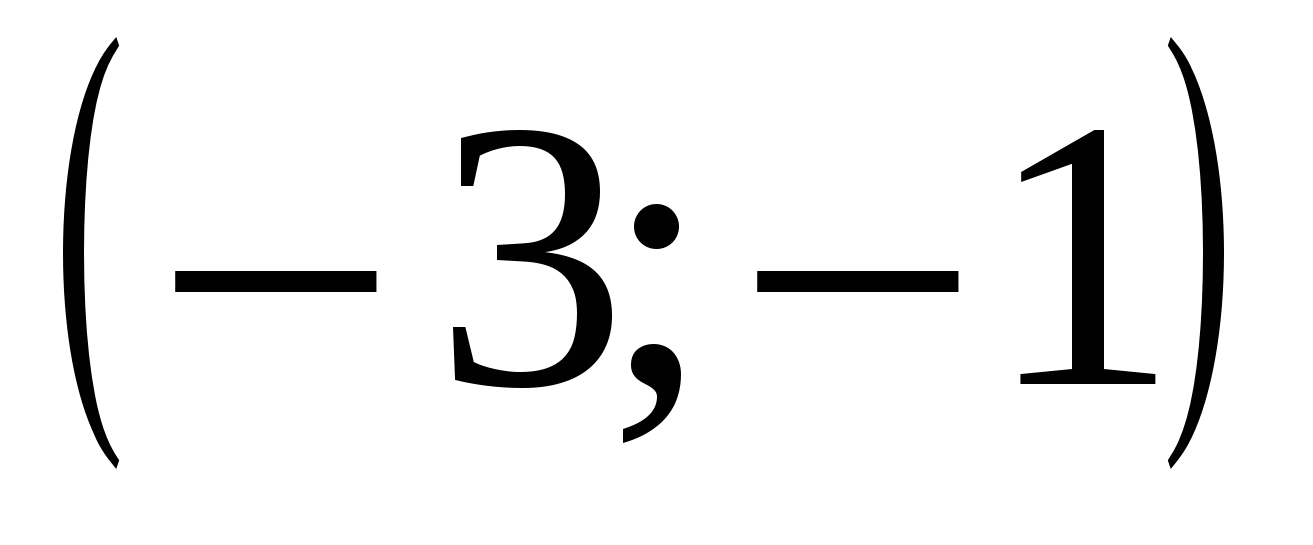
Наибольшее целое значение х, удовлетворяющее неравенству
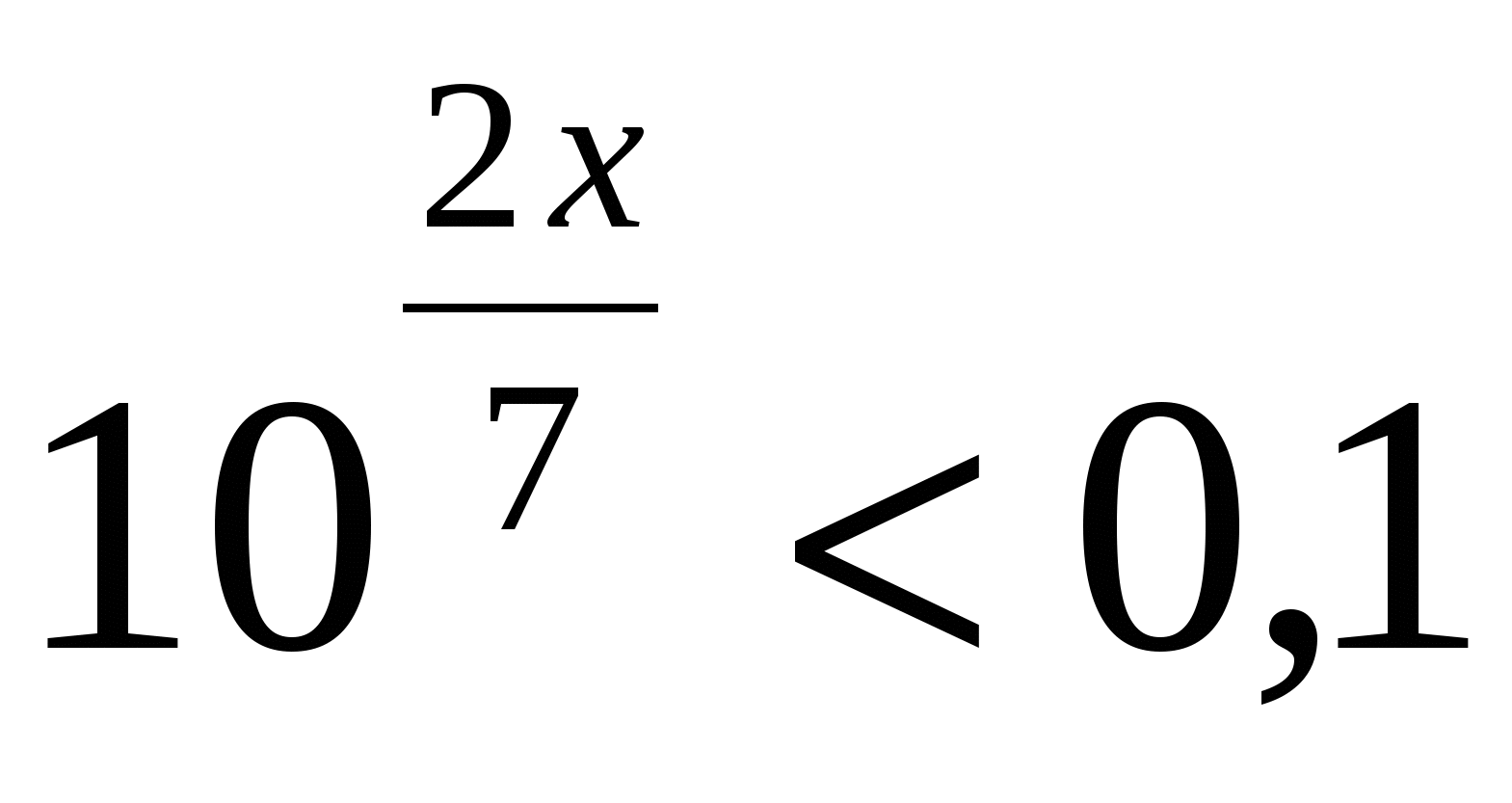 , равно
, равно1) -3
2) -4
3) 0
4) не существует
Наименьшее целое значение х, удовлетворяющее неравенству
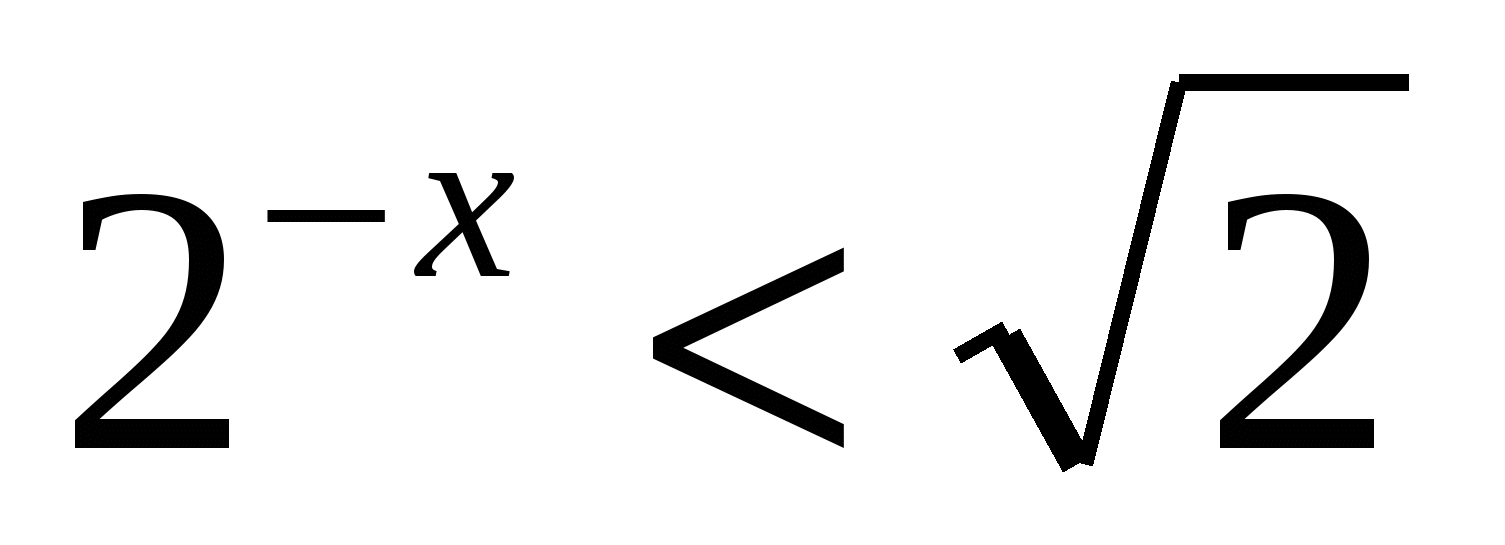 , равно
, равно1) 0
2) -1
3) 1
4) не существует
Наименьшее целое значение х, удовлетворяющее неравенству
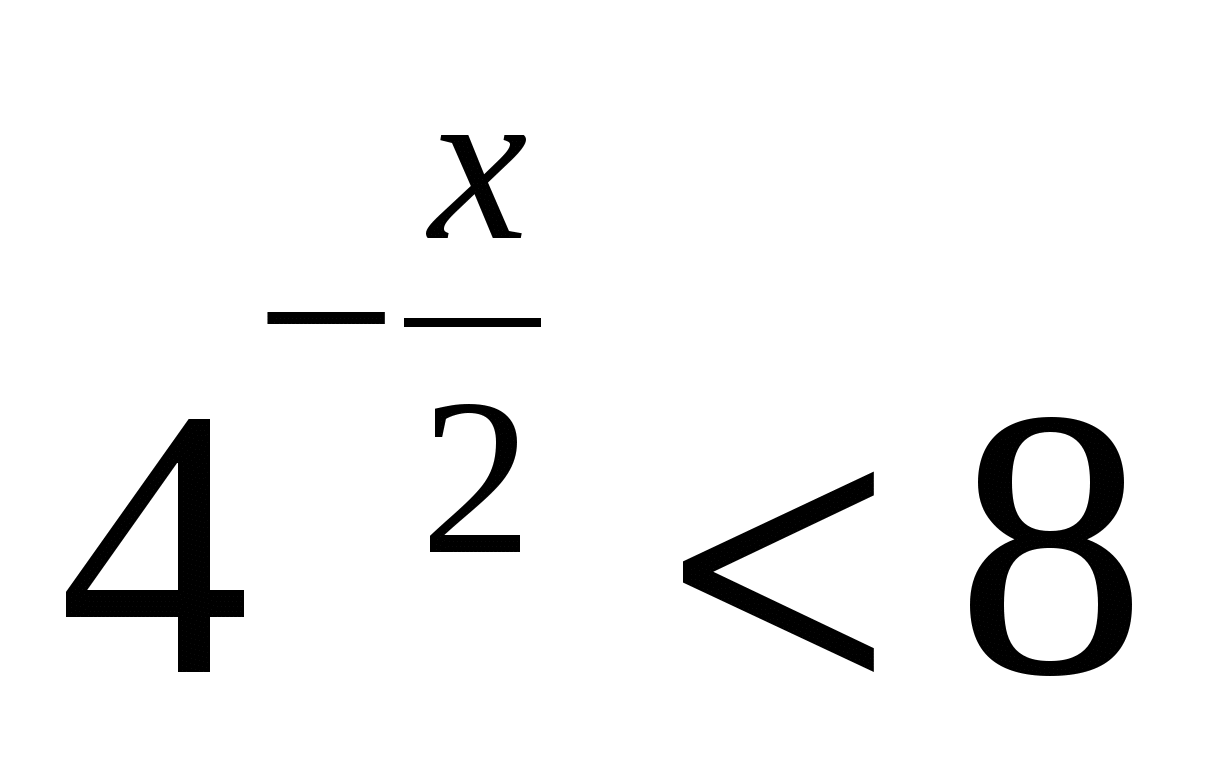 , равно
, равно
1) -4
2) -3
3) -2
4) не существует
Вариант 2.
Тест по теме «Показательная функция»
Из приведенных ниже функций укажите показательную:
а) у=х7 б) ![]() в)
в) ![]() г)
г) ![]()
1) а и в
2) а и б
3) в и г
4) б и г
Из приведенных ниже утверждений верными являются:
а) функция ![]() не принимает значение 0;
не принимает значение 0;
б) функция ![]() является четной;
является четной;
в) функция ![]() пересекает ось Оу в точке (0; 1);
пересекает ось Оу в точке (0; 1);
г) функция ![]() принимает только неотрицательные значения.
принимает только неотрицательные значения.
1) а и в
2) а и б
3) в и г
4) б и г
При каких значениях х выражении
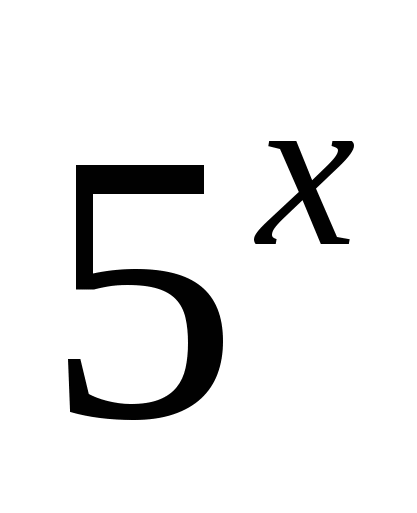 меньше 1?
меньше 1?1) x>0
2) x<0
3) x>1
4) x<1
Областью значений функции
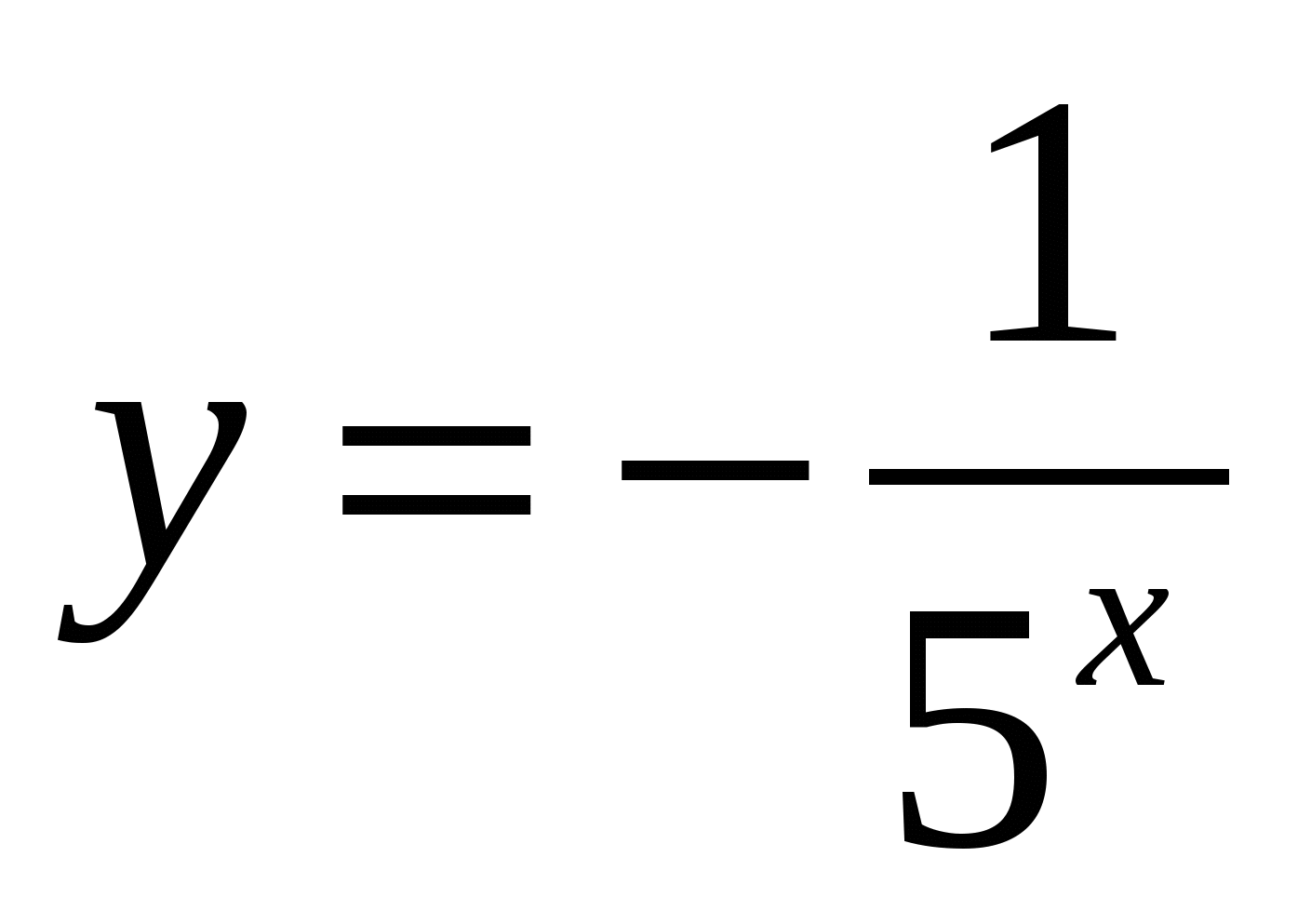 является множество
является множество1)
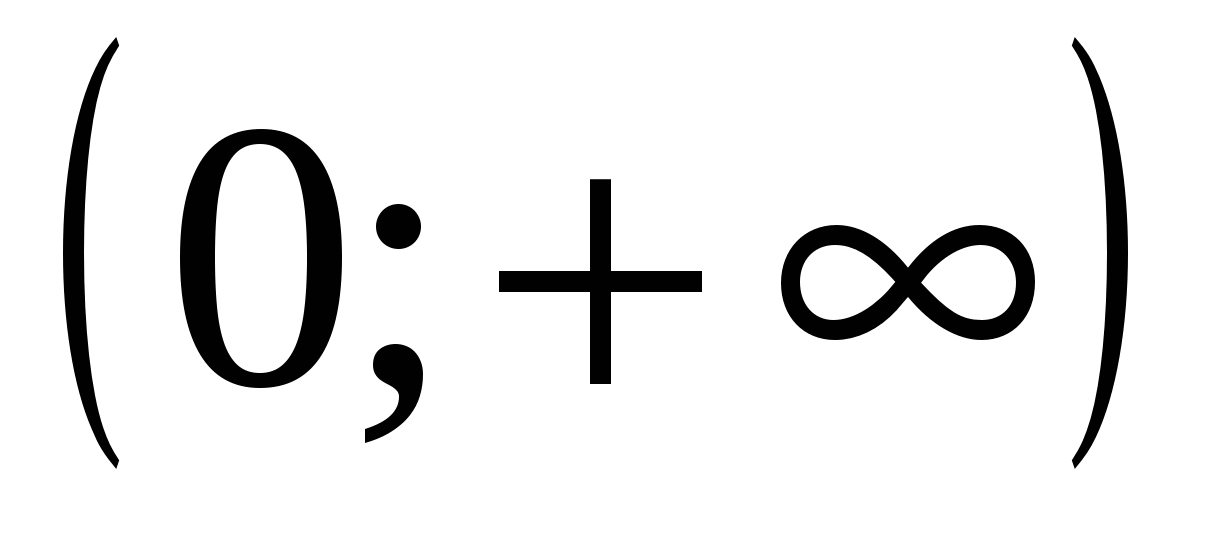
2)
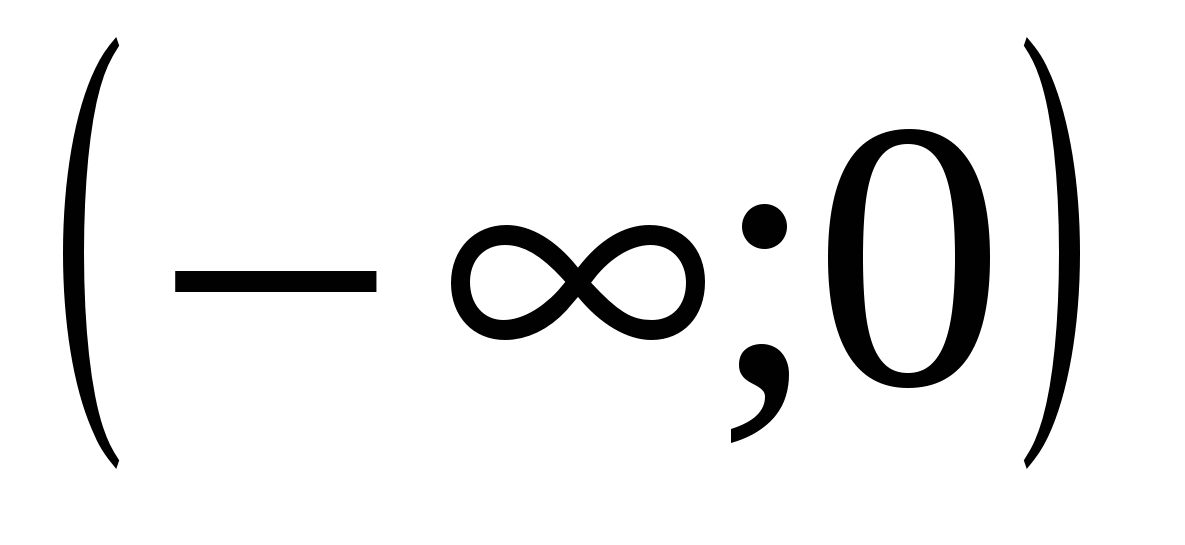
3)
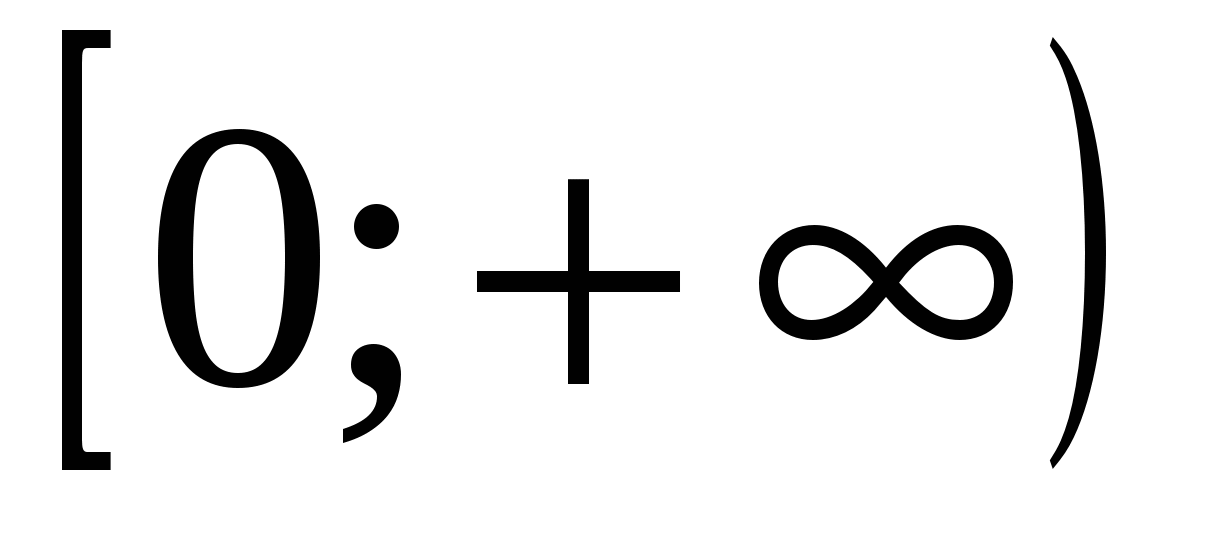
4)
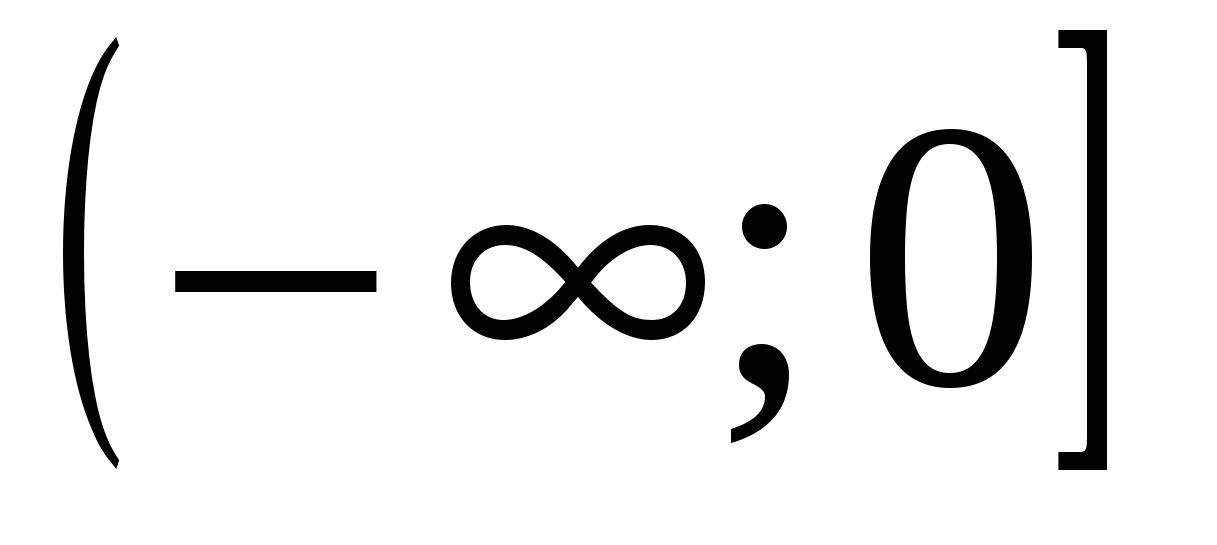
Из приведенных ниже утверждений верными являются:
а) графики функций ![]() и
и ![]() симметричны относительно оси ординат;
симметричны относительно оси ординат;
б) графики функций ![]() и
и ![]() не пересекают ось Ох;
не пересекают ось Ох;
в) графики функций ![]() и
и ![]() симметричны относительно оси абсцисс;
симметричны относительно оси абсцисс;
г) графики функций ![]() и
и ![]() пересекают ось Оу в разных точках.
пересекают ось Оу в разных точках.
1) а и в
2) а и б
3) в и г
4) б и г
Из приведенных ниже функций укажите убывающие:
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
1) а и в
2) а и б
3) в и г
4) б и г
Корень уравнения
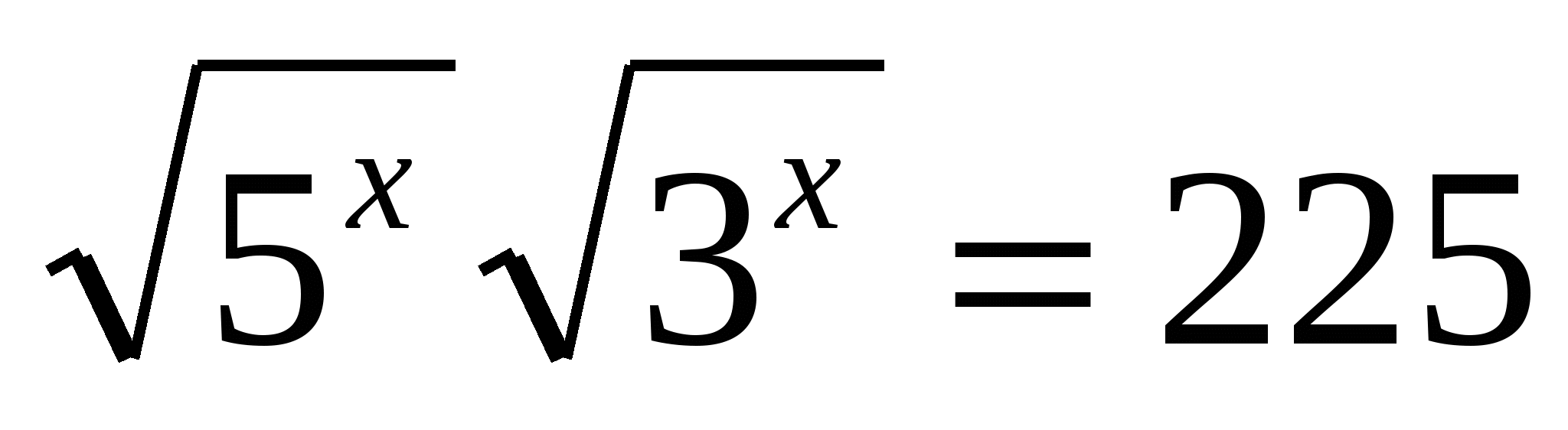 равен
равен1) 1
2) 2
3) 3
4) 4
Произведение корней уравнения
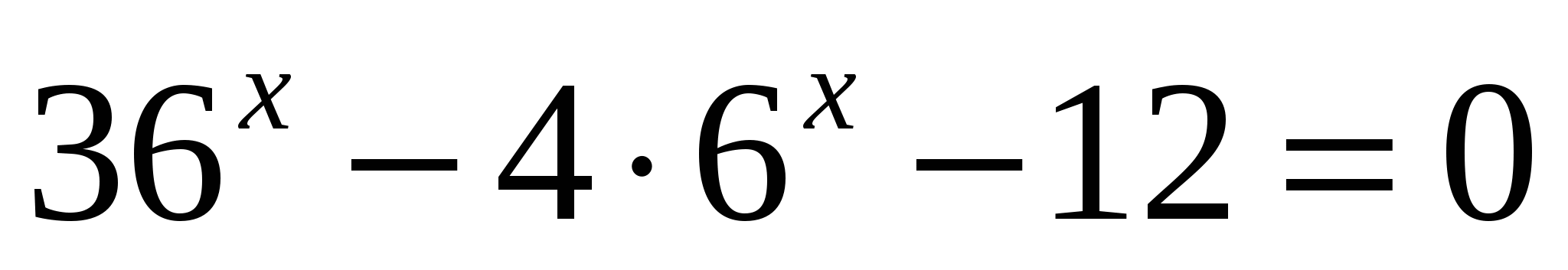 равна
равна1) 4
2) -12
3) 1
4) -2
Сумма корней уравнения
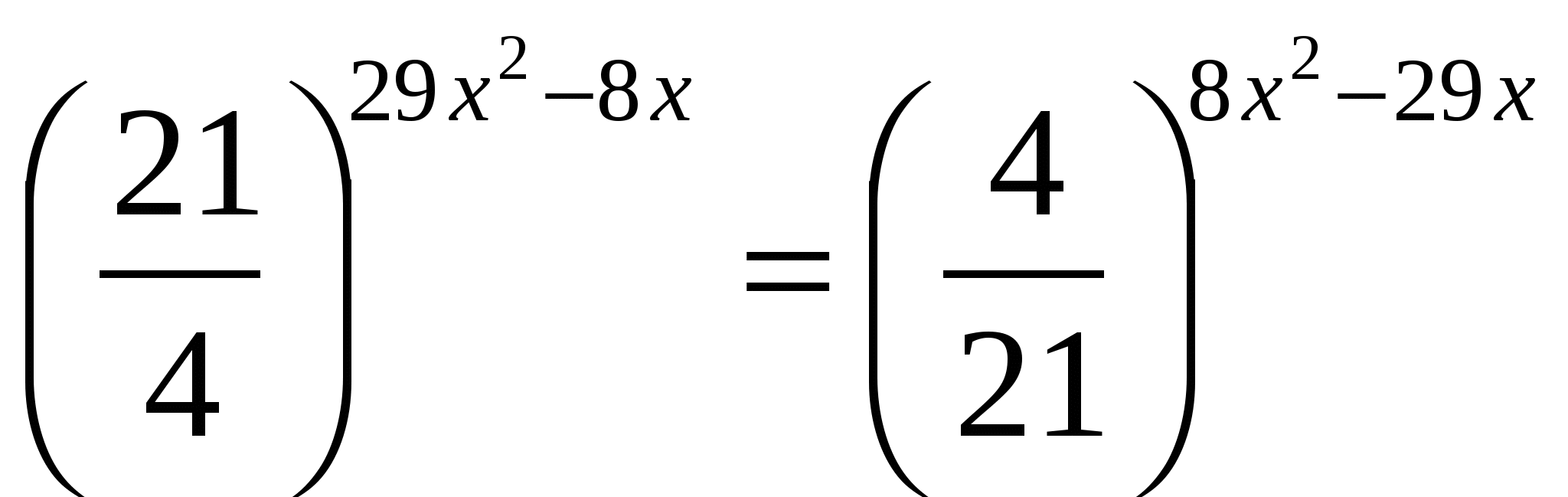 равно
равно1) -37
2) 37
3) 1
4) -1
Сумма корней уравнения
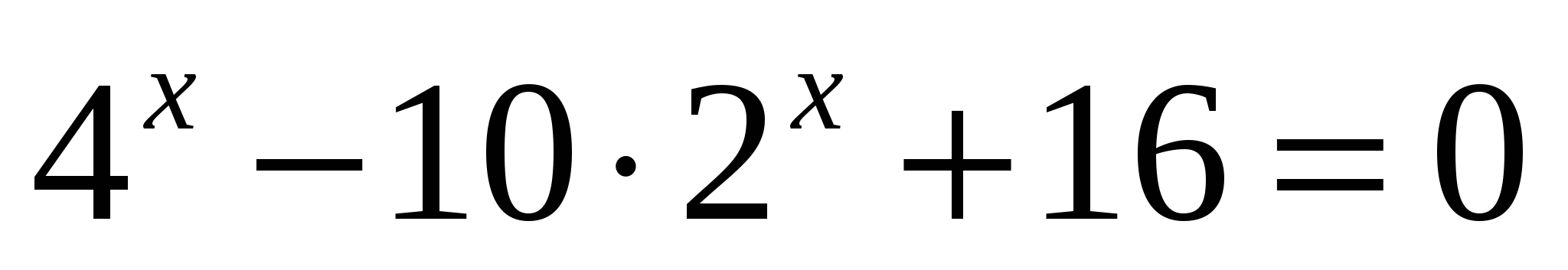 равна
равна1) -10
2) 10
3) -4
4) 4
Выражение 0,3+а, где а - корень уравнения
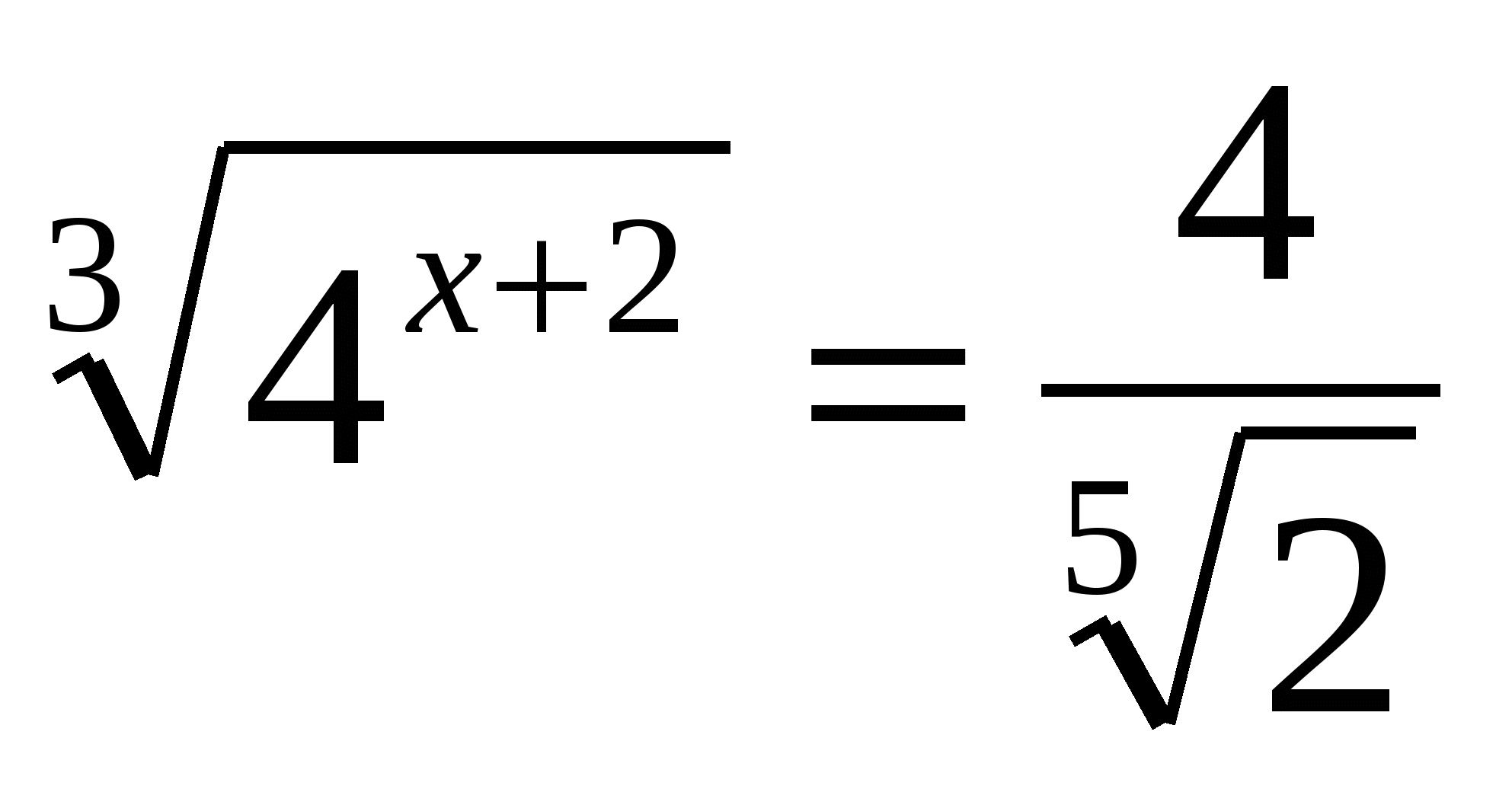 , равно
, равно1) 0,7
2) 1
3) 2,7
4) 5
Наибольшее целое значение х, удовлетворяющее неравенству
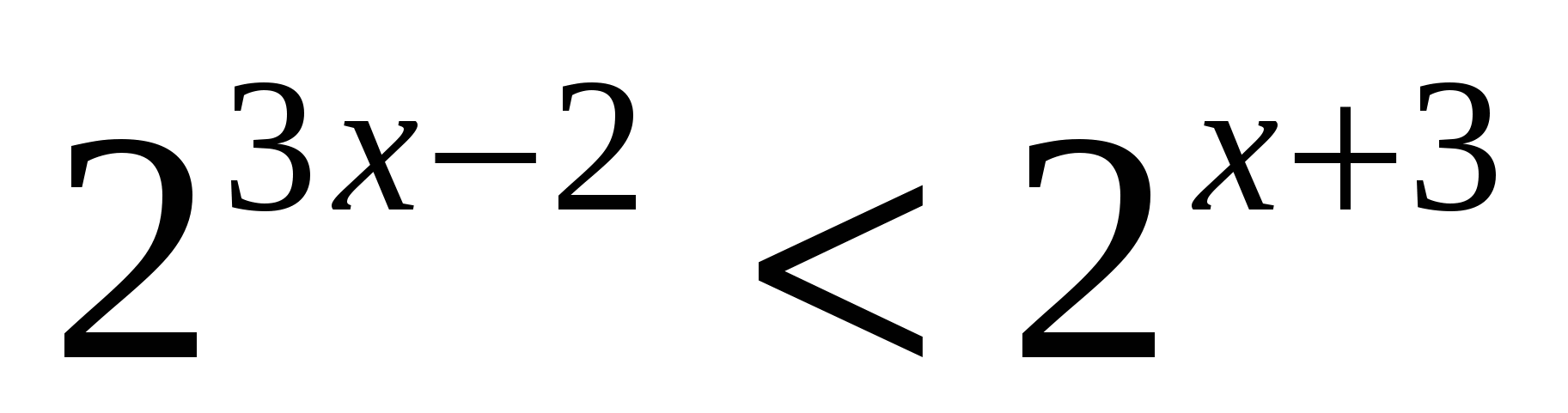 , равно
, равно1) 2
2) 3
3) 0
4) не существует
Количество натуральных решений неравенства
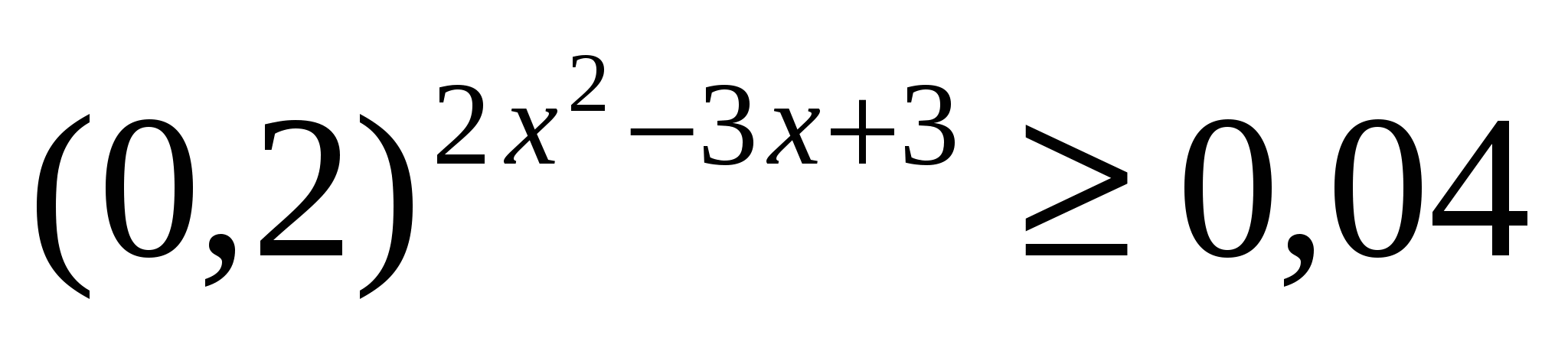 равно
равно1) 1
2) 2
3) 3
4) нет ответа
Наименьшее целое значение х, удовлетворяющее неравенству
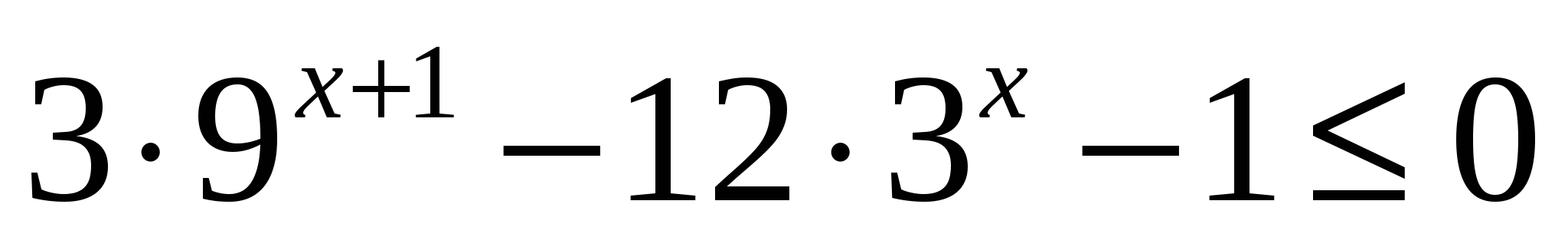 , равно
, равно1) -2
2) 0
3) 2
4) -1
Наибольшее целое значение х, удовлетворяющее неравенству
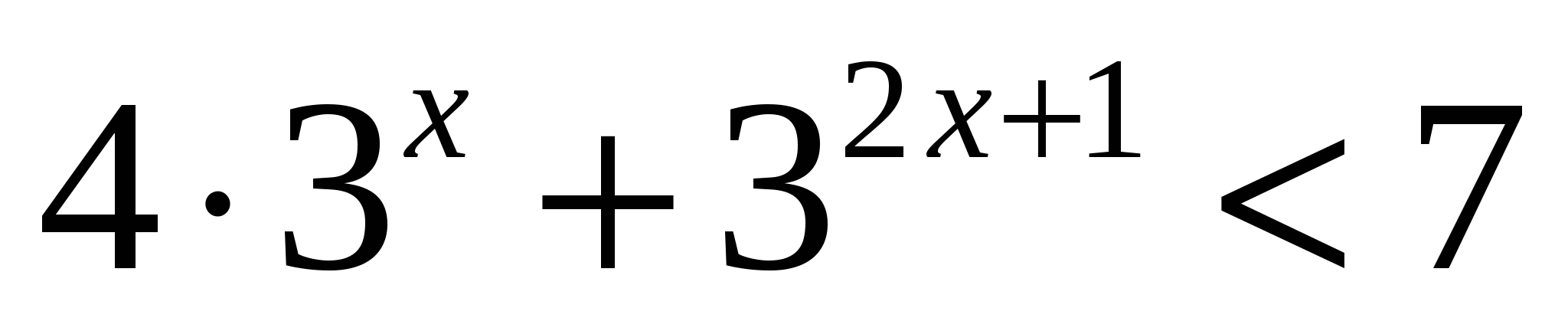 , равно
, равно
1) 1
2) 0
3) -1
4) не существует
Ответы:
Вариант 1.
Вариант 2.
4
4
3
1
1
2
2
2
2
4
2
2
4
4
3
3
3
3
1
4
3
2
2
1
2
1
3
1
3
3

Нравится материал? Поддержи автора!
Ещё документы из категории алгебра:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ