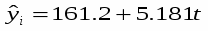
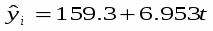
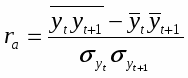
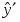
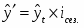
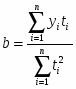
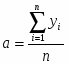
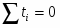
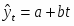
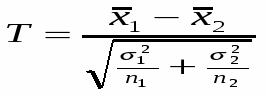
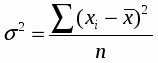
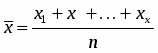
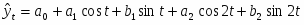
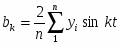
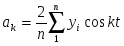
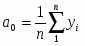
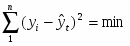
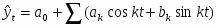
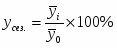
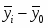Министерство образования Республики Беларусь

МОГИЛЕВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра экономической информатики

Курсовая работа

по статистике предприятия

Тема: ”Сравнительный анализ динамики и выявление внутригодовых колебаний розничного товарооборота области”

Руководитель Ливинская В. А.

Могилев 2001

Содержание:

1. Постановка задачи …………………………………………….. стр.

2. Описание экономических понятий, используемых в работе….. стр.

3. Описание методов расчета динамических рядов …………… стр.

3.1 Понятие сезонной неравномерности и ее характеристика…… стр.

3.2 Корреляционная зависимость между уровнями

различных рядов динамики ……………………………………… стр.

4. Результаты работы программы ………………………………. стр.

Список литературы ……………………………………………. стр.

Приложение А …………..………………………………………. стр.

1. Постановка задачи.

По исходным данным необходимо произвести анализ динамических рядов, который включает в себя определение существования тренда и его уравнения, выявление наличия сезонных колебаний, анализ динамики сезонной волны, экстраполяцию на один год, линию тренда, фактические уровни ряда динамики, центрированную скользящую среднюю.

2. Описание экономических понятий, используемых в работе.

Товарооборот – это процесс обращения товаров, экономический показатель, отражающий совокупную стоимость продаж средств производства и предметов потребления.

Различают оптовый и розничный товарооборот. Оптовый товарооборот включает объем продаж товаров производственными и сбытовыми предприятиями организациям розничной торговли и предприятиям для промышленной переработки. Розничный товарооборот включает объем продаж товаров и услуг населению розничной торговой сетью, предприятиями общественного питания, а также ателье, ремонтными мастерскими и т.п.

3. Описание методов расчета динамических рядов.

3.1 Понятие сезонной неравномерности и ее характеристика.

Слагаясь под совместным воздействием систематических и случайных факторов, уровень ряда динамики испытывает также воздействие причин, обусловленных периодичностью колебаний.

В рядах внутригодичной динамики, можно выделить три важнейшие составляющие колеблемости уровней временного ряда:

тренд, сезонную и случайную компоненты.

Таким образом, при анализе колеблемости динамических рядов наряду с выделением случайных колебаний возникает и задача изучения периодических колебаний. Как правило, изучение периодических («сезонных») колебаний необходимо с целью исключения их влияния на общую динамику для выявления «чистой» (случайной ) колеблемости.

В широком понимании к сезонным относят все явления, которые обнаруживают в своем развитии отчетливо выраженную закономерность внутригодичных изменений, т.е. более или менее устойчиво повторяющиеся из года в год колебания уровней. Часто эти колебания могут быть не связаны со сменой времен года. К сезонным явлениям относят, например, потребление электроэнергии; неравномерность производственной деятельности в отраслях пищевой промышленности, связанных с переработкой сельскохозяйственного сырья; перевозки пассажирским транспортом, спрос на многие виды продукции и услуг и т.д.

Как бы ни проявлялась сезонность, она наносит большой ущерб национальной экономике, связанный с неравномерным использованием оборудования и рабочей силы, с неравномерной загрузкой транспорта, необходимостью создания резервов мощностей и т.д. Комплексное регулирование сезонных изменений по отдельным отраслям должно основываться на исследовании сезонных отклонений.

Важнейшими задачами, решаемыми в ходе исследования сезонности, являются следующие:

1) определение наличия сезонности, численное выражение проявления сезонных колебаний и выявление их силы и характера в различных фазах годичного цикла;

2) характеристика факторов, вызывающих сезонные колебания;

3) оценка последствий, к которым приводит наличие сезонных колебаний;

4) математическое моделирование сезонности. Для измерения сезонных колебаний статистикой предложены различные методы. Наиболее простые и часто употребляемые

из них:

а) метод абсолютных разностей;

б) метод относительных разностей;

в) построение индексов сезонности.

Первые два способа предполагают нахождение разностей фактических уровней и уровней, найденных при выявлении основной тенденции развития.

Применяя способ абсолютных разностей, оперируют непосредственно размерами этих разностей, а при использовании метода относительных разностей определяют отношение абсолютных размеров указанных разностей к выравненному уровню. При выявлении основной тенденции используют либо метод скользящей средней, либо аналитическое выравнивание. В некоторых случаях в стационарных рядах можно пользоваться разностью фактических уровней и средним месячным уровнем за год. Использование данных за несколько лет связано с тем обстоятельством, что в отклонениях по отдельным годам сезонные колебания смешиваются со случайными. Чтобы элиминировать случайные колебания, берут средние отклонения за несколько лет.

Для выделения сезонной волны надо определить средний уровень товарооборота за каждый месяц по пятилетним данным и общую среднюю за весь рассматриваемый период.

Общая средняя уд получается делением суммы уровней отпуска за все пять лет на 60 (общее число месяцев).

Затем определяется абсолютное отклонение средних месячных показателей от общей средней .

Метод относительных разностей является развитием метода абсолютных разностей. Для нахождения относительных разностей абсолютные отклонения делят на общую среднюю и выражают в процентах.

Вместо относительных разностей за каждый месяц может быть вычислен индекс сезонности, который рассчитывается как отношение среднего уровня соответствующего месяца к общей средней, т.е.

.

Выделение сезонной волны можно выполнить на основе построения аналитической модели проявления сезонных колебаний.

Построение аналитической модели выявляет основной закон колеблемости данного временного ряда в связи с переходом от месяца к месяцу и дает среднюю характеристику внутригодичных колебаний.

При исследовании явлений периодического типа в качестве аналитической формы развития во времени принимается уравнение следующего типа (ряд Фурье):

В этом уравнении величина k определяет гармонику ряда Фурье и может быть взята с разной степенью точности (чаще всего от 1 до 4). Для отыскания параметров уравнения используется метод наименьших квадратов, т.е.

Найдя частные производные этой функции и приравняв их к нулю, получим систему нормальных уравнений, решение которой дает следующие формулы для вычисления параметров:

;

;

;

Параметры уравнения зависят от значений у и связанных с ними последовательных значений cos kt и sin kt.

Для изучения сезонных колебаний на протяжении года необходимо взять n=12 (по числу месяцев в году). Тогда, представляя периоды как части длины окружности, ряд динамики можно записать в виде таблицы, в первой строке которой будут записаны периоды, а во второй – соответствующие им уровни.

Применяя к этим же данным вторую гармонику ряда Фурье для выражения модели сезонности, получим коэффициенты a₂ и b_2. Подставляя их в уравнение ряда Фурье, будем иметь следующую модель сезонности данного ряда динамики:

.

Рассмотрим выявление всех типов колебаний внутригодичной динамики уровней.

Для выравнивания уровней принимаем период сглаживания, равный четырем кварталам (m = 4).

Найденные скользящие средние будут отнесены не к конкретному кварталу, а попадут в промежуток между ними.

Для отнесения скользящей средней к определенному кварталу, находим средние из двух смежных скользящих средних, т.е. производим центрированные средних.

Для выявления сезонной составляющей в колеблемости уровней ряда динамики рассчитываем отношения фактических объемов товарооборота каждого квартала к соответствующей ему скользящей средней.

На основании полученных соотношений выполняется их группировка по кварталам путем занесения значений в таблицу.

Для расчета индекса сезонности на основании сравнений фактических квартальных значений за ряд лет с соответствующей скользящей средней можно воспользоваться следующими приемами:

1) рассчитать для каждого квартала среднюю арифметическую из полученных соотношений.

2) определить медиану из значений индексов сезонности за каждый квартал путем ранжирования.

Т. к. обычно сумма индексов сезонности хотя и незначительно, но отличается от 4 (для четырех кварталов сумма индексов должна быть равна 4, а их средняя равна 1,00), то для устранения этих расхождений определяется поправочный коэффициент как отношение теоретической суммы индексов (4,0) к фактической величине их суммы.

Для расчета индексов сезонности, скорректированных на поправочный коэффициент используются значения медиан.

Прежде чем анализировать основную тенденцию (тренд) или циклические колебания, необходимо исключить сезонную компоненту и проверить гипотезу о существовании тренда.

Для этого можно использовать метод проверки разностей средних уровней. Суть этого метода состоит в делении ряда на две части и нахождении их средних и дисперсий по формулам:

,

где n – число уровней ряда;

;

Затем мы находим расчетное значение с помощью статистики Стьюдента:

;

Затем полученное значение сравниваем с критическим табличным значением , которое равно 3,18 (число степеней свободы равно n1 + n2 - 2).

Сравнив критическое значение с расчетным, делаем вывод о наличии или отсутствии тренда в рыду динамики.

В нашем случае Трасч. = 5,0528 и 4,2246 для первого и второго варианта соответственно. Т. к. в обоих случаях Тр. > Ткр., то гипотезу об отсутствии тренда отклоняем.

После ее исключения из колеблемости уровней временного ряда, рассчитаем уравнение тренда, воспользовавшись линейной функцией

,

где ;

;

;

С помощью полученного уравнения тренда выполним экстраполяцию на один год.

Найденные таким образом значения не учитывают сезонные колебания в объеме товарооборота. Для учета сезонной составляющей уровень, полученный в результате экстраполяции, умножают на индекс сезонности, т.е.

где - экстраполируемый уровень с учетом сезонных колебаний.

3.2 Корреляционная зависимость между уровнями различных рядов динамики.

Применение методов классической теории корреляции в динамических рядах связано с некоторыми особенностями. Прежде всего это наличие для большинства динамических рядов зависимости последующих уровней от предыдущих.

Наличие зависимости между последующими и предшествующими уровнями динамического ряда в статистической литературе называют автокорреляцией.

Коэффициент автокорреляции вычисляется по непосредственным данным рядов динамики, когда фактические уровни одного ряда рассматриваются как значения факторного признака, а уровни этого же ряда со сдвигом на один период принимаются в качестве результативного признака.

Коэффициент автокорреляции рассчитывается на основе формулы коэффициента корреляции для парной зависимости:

,

где y_t – фактические уровни ряда, а y_t+1 – уровни того же ряда со сдвигом на 1 период.

4. Результаты работы программы.

Таблица 1 – Исходные данные (1 вариант).

Год

Янв.

Февр.

Март

Апр.

Май

Июнь

Июль

Авг.

Сент.

Окт.

Нояб.

Дек.

Итого

1-ый

92,4

77

50

36,6

67,5

53,3

70

74,8

80

85

95

106,4

888

2-ой

105

89

70

59

75

70

83

90

99

100

105

120

1065

3-ий

125

120

105

101

125

110

137

139

150

149

160

190

1611

4-ый

195

185

177

175

195

190

210

215

230

230

240

270

2512

5-ый

276

264

261

260

280

275

297

299

315

310

315

350

3502

Итого за весь период

793,4

735

663

631,6

742,5

698,3

797

817,8

874

874

915

1036,4

9578

Средний уровень за месяц

158,68

147

132,6

126,32

148,5

39,66

159,4

163,56

174,8

174,8

183

207,28

159,63333

Абсолютное отклонение от общей средней

-0,9533333

-12,633333

-27,033333

-33,313333

-11,133333

-19,973333

-0,2333333

3,9266667

15,166667

15,166667

23,366667

47,646667

 

Относительное отклонение от общей средней (в %)

-0,5972019

-7,9139695

-16,934642

-20,868657

-6,9743161

-12,512007

-0,1461683

2,4598037

9,5009397

9,5009397

14,637711

29,847567

 

Индекс сезонности

99,402798

92,08603

83,065358

79,131343

93,025684

87,487993

99,853832

102,4598

109,50094

109,50094

114,63771

129,84757

 

Таблица 2 – Исходные данные (2 вариант).

Год

Янв.

Февр.

Март

Апр.

Май

Июнь

Июль

Авг.

Сент.

Окт.

Нояб.

Дек.

Итого

1-ый

81,8

81

67,8

50,4

76,1

62

88

94,2

100

118

110,4

125

1054,999

2-ой

120

110

105

102

110

101

126

130

140

145

139

150

1478

3-ий

150

130

130

125

135

129

147

152

163

165

157

175

1758

4-ый

170

160

155

155

170

170

190

200

210

225

223

250

2278

5-ый

249

241

239

236

250

247

259

270

280

285

281

300

3137

Итого за весь период

770,8

722

696,8

668,4

741,1

709

810

846,2

893

938

910,4

1000

9705,7

Средний уровень за месяц

154,16

144,4

139,36

133,68

148,22

141,8

162

169,24

178,6

187,6

182,08

200

161,761

Абсолютное отклонение от общей средней

-7,602

-17,362

-22,402

-28,082

-13,542

-19,962

0,238

7,478

16,838

25,838

20,318

38,238

 

Относительное отклонение от общей средней (в %)

-4,699

-10,733

-13,849

-17,36

-8,371

-12,34

0,147

4,623

10,409

15,973

12,561

23,639

 

Индекс сезонности

95,301

89,267

86,151

82,64

91,629

87,66

100,147

104,623

110,409

115,973

112,561

123,639

 

Таблица 3 – Построение модели сезонной волны на основе гармоник ряда Фурье (1 вариант).

Удельный розничный товарооборот области по месяцам

y cos t

y sin t

yt

y cos 2t

y sin 2t

yt

y cos 3t

y sin 3t

yt

y cos 4t

y sin 4t

yt

158,68

158,68

0

166,242

158,68

0

170,618

158,68

0

157,127

158,68

0

152,293

147

127,306

73,5

152,273

73,5

127,306

146,902

-6,426

147

147,764

-73,5

127,306

148,646

132,6

66,3

114,835

140,277

-66,3

114,835

130,529

-132,6

-1,159

154,781

-66,3

-114,835

158,732

126,32

-5,522

126,32

133,468

-126,32

-1,104

129,091

1,654

-126,32

164,467

126,32

2,209

159,633

148,5

-74,25

128,605

133,669

-74,25

-128,605

139,041

148,5

2,596

159,014

-74,25

128,605

159,896

139,66

-120,949

69,83

140,828

69,83

-120,949

150,576

1,942

139,66

148,819

-69,83

-120,949

152,771

159,4

-159,4

-1,394

153,025

159,4

2,787

157,402

-159,4

-4,18

152,473

159,4

5,574

147,64

163,56

-141,647

-81,78

166,993

81,78

141,647

161,622

-8,448

-163,56

163,599

-81,78

141,647

164,481

174,8

-87,4

-151,381

178,989

-87,4

151,381

169,241

174,8

6,113

166,25

-87,4

-151,381

170,201

174,8

2,084

-174,8

185,799

-174,8

-4,169

181,422

-6,253

174,8

164,467

174,8

8,338

159,633

183

91,5

-158,483

185,598

-91,5

-158,483

190,969

-183

5,09

168,156

-91,5

158,483

169,038

207,28

179,51

-103,64

178,439

103,64

-179,51

188,187

0

-207,28

168,684

-103,64

-179,51

172,636

1915,6

39,649

-156,994

1915,6

26,26

-52,377

1915,6

6,98

-35,7

1915,6

-29

-10,635

1915,6

Таблица 4 – Построение модели сезонной волны на основе гармоник ряда Фурье (2 вариант).

Удельный розничный товарооборот области по месяцам

y cos t

y sin t

yt

y cos 2t

y sin 2t

yt

y cos 3t

y sin 3t

yt

y cos 4t

y sin 4t

yt

154,16

154,16

0

164,822

154,16

0

164,567

154,16

0

158,54

154,16

0

156,138

144,4

125,054

72,2

151,183

72,2

125,054

145,993

-6,312

144,4

150,948

-72,2

125,054

150,172

139,36

69,68

120,689

140,379

-69,68

120,689

135,444

-139,36

-1,218

156,987

-69,68

-120,689

160,165

133,68

-5,843

133,68

135,304

-133,68

-1,169

135,559

1,753

-133,68

164,163

133,68

2,337

161,762

148,22

-74,11

128,362

137,319

-74,11

-128,362

142,509

148,22

2,592

160,532

-74,11

128,362

159,755

141,8

-122,802

70,9

145,883

70,9

-122,802

150,818

1,972

141,8

155,613

-70,9

-122,802

158,792

162

-162

-1,416

158,702

162

2,832

158,447

-162

-4,249

160,18

162

5,665

157,778

169,24

-146,566

-84,62

172,34

84,62

146,566

167,15

-8,74

-169,24

166,218

-84,62

146,566

165,442

178,6

-89,3

-154,672

183,145

-89,3

154,672

178,21

178,6

6,245

164,983

-89,3

-154,672

168,161

187,6

2,237

-187,6

188,219

-187,6

-4,474

188,474

-6,711

187,6

164,163

187,6

8,948

161,762

182,08

91,04

-157,686

186,205

-91,04

-157,686

191,395

-182,08

5,06

169,348

-91,04

157,686

168,571

200

173,205

-100

177,641

100

-173,205

182,576

0

-200

169,463

-100

-173,205

172,642

1941,14

18,361

-158,746

1941,14

-1,53

-35,074

1941,14

-2,46

-29,12

1941,14

-14,41

-13,7

1941,14

Таблица 5 – Выявление типов колебаний внутригодичной динамики уровней временного ряда (1 вариант).

Год

Квартал

Фактический объем товарооборота

Скользящая средняя за 4 квартала

Центрированная скользящая средняя за 4 квартала

Отношение фактического объема товарооборота к скользящей средней

Индекс сезонности

Объем товарооборота, скорректированный на индекс сезонности

1

1

73,133

 

1,036

70,606

 

2

52,467

74

 

0,913

57,451

 

3

74,933

77,717

75,858

0,988

0,995

75,297

 

4

95,467

81,6

79,658

1,198

1,056

90,422

2

1

88

85,533

83,567

1,053

1,036

84,959

 

2

68

88,75

87,142

0,78

0,913

74,46

 

3

90,667

95,917

92,333

0,982

0,995

91,107

 

4

108,333

106,917

101,417

1,068

1,056

102,608

3

1

116,667

119,75

113,333

1,029

1,036

112,635

 

2

112

134,25

127

0,882

0,913

122,64

 

3

142

151,5

142,875

0,994

0,995

142,689

 

4

166,333

170,167

160,833

1,034

1,056

157,543

4

1

185,667

189,25

179,708

1,033

1,036

179,251

 

2

186,667

209,333

199,292

0,937

0,913

204,399

 

3

218,333

229,667

219,5

0,995

0,995

219,393

 

4

246,667

250,917

240,292

1,027

1,056

233,632

5

1

267

272,25

261,583

1,021

1,036

257,774

 

2

271,667

291,833

282,042

0,963

0,913

297,474

 

3

303,667

 

0,995

305,14

 

4

325

 

1,056

307,825

Таблица 6 – Выявление типов колебаний внутригодичной динамики уровней временного ряда (2 вариант).

Год

Квартал

Фактический объем товарооборота

Скользящая средняя за 4 квартала

Центрированная скользящая средняя за 4 квартала

Отношение фактического объема товарооборота к скользящей средней

Индекс сезонности

Объем товарооборота, скорректированный на индекс сезонности

1

1

76,867

 

0,994

77,338

 

2

62,833

87,892

 

0,906

69,359

 

3

94,067

96,592

92,242

1,02

1,025

91,75

 

4

117,8

106,967

101,779

1,157

1,075

109,589

2

1

111,667

116,45

111,708

1

0,994

112,351

 

2

104,333

123,167

119,808

0,871

0,906

115,168

 

3

132

129,417

126,292

1,045

1,025

128,75

 

4

144,667

135,75

132,583

1,091

1,075

134,583

3

1

136,667

141,25

138,5

0,987

0,994

137,505

 

2

129,667

146,5

143,875

0,901

0,906

143,132

 

3

154

152,75

149,625

1,029

1,025

150,208

 

4

165,667

161,583

157,167

1,054

1,075

154,119

4

1

161,667

173,083

167,333

0,966

0,994

162,658

 

2

165

189,833

181,458

0,909

0,906

182,135

 

3

200

210,167

200

1

1,025

195,075

 

4

232,667

230

220,083

1,057

1,075

216,449

5

1

243

247,417

238,708

1,018

0,994

244,49

 

2

244,333

261,417

254,417

0,96

0,906

269,707

 

3

269,667

 

1,025

263,026

 

4

288,667

 

1,075

268,546

Таблица 7 – Соотношение между фактическим товарооборотом и скользящей средней (1вариант).

 

 

Кварталы

 

 

Год

1

2

3

4

1

0,988

1,198

2

1,053

0,78

0,982

1,068

3

1,029

0,882

0,994

1,034

4

1,033

0,937

0,995

1,027

5

1,021

0,963

Таблица 8 – Соотношение между фактическим товарооборотом и скользящей средней (2вариант).

 

 

Кварталы

 

 

Год

1

2

3

4

1

1,02

1,157

2

1

0,871

1,045

1,091

3

0,987

0,901

1,029

1,054

4

0,966

0,909

1

1,057

5

1,018

0,96

Таблица 9 – Расчет индексов сезонности (1 вариант).

Кварталы

Средний арифметический индекс сезонности

Медиана

Скорректированное значение медианы

1

1,034

1,031

1,036

2

0,891

0,909

0,913

3

0,99

0,991

0,995

4

1,082

1,051

1,056

Итого

3,996

3,983

4

Поправочный коэффициент

1,001

1,004

Таблица 10 – Расчет индексов сезонности (2 вариант).

Кварталы

Средний арифметический индекс сезонности

Медиана

Скорректированное значение медианы

1

0,993

0,993

0,994

2

0,91

0,905

0,906

3

1,024

1,025

1,025

4

1,09

1,074

1,075

Итого

4,017

3,997

4

Поправочный коэффициент

0,996

1,001

Таблица 11 – Расчет параметров линейного уравнения тренда (1 вариант).

Год

Квартал

Объем товаооборота без учета сезонности

Условные обозначения периодов, ti

ti^2

yi * ti

^yi

^yi, скорректированный с учетом сезонности, ^yi * iсез.

1

1

70,606

-19

361

-1341,519

27,244

28,219

 

2

57,451

-17

289

-976,664

41,152

37,582

 

3

75,297

-15

225

-1129,453

55,059

54,793

 

4

90,422

-13

169

-1175,483

68,967

72,815

2

1

84,959

-11

121

-934,551

82,874

85,84

 

2

74,46

-9

81

-670,138

96,782

88,385

 

3

91,107

-7

49

-637,746

110,689

110,155

 

4

102,608

-5

25

-513,042

124,597

131,548

3

1

112,635

-3

9

-337,906

138,504

143,461

 

2

122,64

-1

1

-122,64

152,412

139,189

 

3

142,689

1

1

142,689

166,319

165,516

 

4

157,543

3

9

472,63

180,227

190,282

4

1

179,251

5

25

896,255

194,134

201,082

 

2

204,399

7

49

1430,796

208,041

189,993

 

3

219,393

9

81

1974,534

221,949

220,877

 

4

233,632

11

121

2569,948

235,856

249,016

5

1

257,774

13

169

3351,062

249,764

258,703

 

2

297,474

15

225

4462,114

263,671

240,796

 

3

305,14

17

289

5187,38

277,579

276,239

 

4

307,825

19

361

5848,684

291,486

307,749

Итого

 

3187,306

2660

18496,949

Таблица 12 – Расчет параметров линейного уравнения тренда (2 вариант).

Год

Квартал

Объем товаооборота без учета сезонности

Условные обозначения периодов, ti

ti^2

yi * ti

^yi

^yi, скорректированный с учетом сезонности, ^yi * iсез.

1

1

77,338

-19

361

-1469,421

62,843

62,46

 

2

69,359

-17

289

-1179,095

73,206

66,319

 

3

91,75

-15

225

-1376,255

83,57

85,68

 

4

109,589

-13

169

-1424,656

93,933

100,972

2

1

112,351

-11

121

-1235,864

104,297

103,662

 

2

115,168

-9

81

-1036,514

114,661

103,874

 

3

128,75

-7

49

-901,247

125,024

128,181

 

4

134,583

-5

25

-672,915

135,388

145,532

3

1

137,505

-3

9

-412,514

145,751

144,863

 

2

143,132

-1

1

-143,132

156,115

141,428

 

3

150,208

1

1

150,208

166,479

170,682

 

4

154,119

3

9

462,357

176,842

190,092

4

1

162,658

5

25

813,289

187,206

186,065

 

2

182,135

7

49

1274,946

197,569

178,982

 

3

195,075

9

81

1755,676

207,933

213,183

 

4

216,449

11

121

2380,939

218,297

234,653

5

1

244,49

13

169

3178,367

228,66

227,267

 

2

269,707

15

225

4045,607

239,024

216,537

 

3

263,026

17

289

4471,446

249,387

255,684

 

4

268,546

19

361

5102,367

259,751

279,213

Итого

 

3225,938

2660

13783,59

Таблица 13 – Экстраполяция на один год (1 вариант).

Квартал

Условное обозначение периода

^yi

^yi, скорректированный с учетом сезонности

1

21

305,394

316,324

2

23

319,301

291,6

3

25

333,209

331,6

4

27

347,116

366,483

Таблица 14 – Экстраполяция на один год (2 вариант).

Квартал

Условное обозначение периода

^yi

^yi, скорректированный с учетом сезонности

1

21

270,115

268,469

2

23

280,478

254,091

3

25

290,842

298,185

4

27

301,206

323,774

Таблица 15 –Автокорреляция (1 вариант).

Год

Объем товарооборота

Объем товарооборота со сдвигом в 1 год

yt * (y(t+1))

yt^2

1

888

1065

945720

788544

2

1065

1611

1715715

1134225

3

1611

2512

4046832

2595321

4

2512

3502

8797024

6310144

5

3502

888

3109776

12264004

Итого

9578

9578

18615068

23092238

Таблица 16 –Автокорреляция (2 вариант).

Год

Объем товарооборота

Объем товарооборота со сдвигом в 1 год

yt * (y(t+1))

yt^2

1

1054,7

1478

1558846,5

1112392

2

1478

1758

2598324

2184484

3

1758

2278

4004724

3090564

4

2278

3137

7146086

5189284

5

3137

1054,7

3308593,8

9840769

Итого

9705,7

9705,7

18616574

21417492

В нашем случае уравнение тренда и коэффициент автокорреляции соответственно для первого варианта имеют следующий вид: ;

r_a = 0,0586;

Для второго варианта: ;

r_a = -0,0856;

Список литературы

1. Шмойлова Р. А. Теория статистики, М.: Финансы и статистика, 1996г.

2. Ефимова М. Р., Петрова Е. В., Румянцев В. Н. Общая теория статистики, М.: Инфра-Н, 2000г.

3. Щедрин Н.И., Егоров Н.Н. Статистика торговли: Учебное пособие.- М.:

Финансы и статистика, 1987.

4. Советский энциклопедический словарь /Гл. ред. А. М. Прохоров., М.: Сов. Энциклопедия, 1988г.