Розробка та аналіз математичної моделі технологічного об єкта із заданими параметрами

























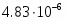



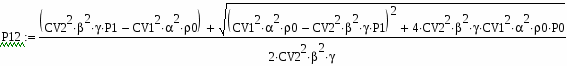
Розробка та аналіз математичної моделі технологічного об' єкта із заданими параметрами
1 Аналітичне моделювання статичного режиму

Рис. 1
Розрахувати статичну модель  і побудувати статичну характеристику повітряного ресиверу для випадку ізотермічного розширення газу.
і побудувати статичну характеристику повітряного ресиверу для випадку ізотермічного розширення газу.
G1=25
G2=25
p0=6
p=2
p1=1,5
Визначимо границі об’єкту моделювання, його виходи і входи. У відповідності з математичною моделю маємо 1 вихідну величину – Р і 2 вхідні  та
та  . Виличини Р0 і Р1 будемо вважати постійними. Складемо рівняння математичного балансу.
. Виличини Р0 і Р1 будемо вважати постійними. Складемо рівняння математичного балансу.
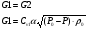

Де  та
та  - коефіцієнти витрати клапанів;
- коефіцієнти витрати клапанів;  та
та  значення щільності газу відповідно для Р0 і Р1
значення щільності газу відповідно для Р0 і Р1

Це рівняння є рівнянням статики, яке зв’язує вихідну величину Р зі вхідними  та
та  .
.
Але в цьому рівняння присутні значення значення щільності газу  та
та  , які для ізотермічного процесу повністю визначаються значеннями тиску Р0 і Р1.
, які для ізотермічного процесу повністю визначаються значеннями тиску Р0 і Р1.
І в зв’язку з тим, що Р0, а значить, і  являються постійними величинами, тиск слід виразити через значення щільності.
являються постійними величинами, тиск слід виразити через значення щільності.
Для ізотермічного процесу, який протікає при постійній температурі з рівнянням стану ідеального газу.
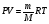
З цієї формули слідує, що при постійній температурі і незмінному значенні маси газу і його молярній масі М добуток тиску газу на його об’єм повинно залишатися постійною.

Відомо, що :






Значення функціональної залежності  отримано в загальному вигляді. Перейдемо до чисельного представлення отриманої функціональної залежності. Для цього визначаємо чисельне значення усіх необхідних величин ( основного статичного режиму).
отримано в загальному вигляді. Перейдемо до чисельного представлення отриманої функціональної залежності. Для цього визначаємо чисельне значення усіх необхідних величин ( основного статичного режиму).
Таблиця 1
Значення параметрів ресивера в номінальному статичному режимі
№
Назва параметру
Позначення
Розмірність
Дані
1
Витрати повітря на вході
G1
кг/год
20
2
Витрати повітря на виході
G2
кг/год
20
3
Тиск повітря на вході
P0
кг/см2
6
4
Тиск повітря в ресивері
P
кг/см2
4
5
Тиск повітря на виході
P1
кг/см2
3
6
Ступінь відкриття вхідного клапану
-
0.4
7
Ступінь відкриття вихідного клапану
-
0.6
8
Температура повітря
t
оС
20
9
Щільність повітря
кг/см3
10
Щільність повітря в ресивері

кг/см3
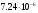
11
Коефіцієнт витрати вхідного клапана
12
Коефіцієнт витрати вихідного клапана
13
З довідника відомо, що  при тиску і температури 200С дорівнює
при тиску і температури 200С дорівнює 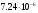 кг/см2
кг/см2


Отримана залежність - статична модель об'єкта в явній формі, що відповідає поставленому завданню. Розрахуємо характеристику 

Р кг/см2
0
3
0,1
3,116
0,2
3,386
0,3
3,7
0,4
4
0,5
4,269
0,6
4,5
0,7
4,698
0,8
4,866
0,9
5,008
1
5,128
2 Аналітичне моделювання динамічного режиму
Отримати рівняння динаміки двохємкістного ресивера, схематично зображеного на рис.1. Визначальним параметром даного об’єкта є тиск Р3. Необхідно знайти залежність:
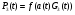 , де
, де  ступінь відкриття клапану на вхідному потоці;
ступінь відкриття клапану на вхідному потоці; 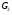 - витрати газу з ресивера, кг/год.
- витрати газу з ресивера, кг/год.

Рис. 2. Розрахункова схема об’єкту моделювання
Основний статичний режим визначається такими значеннями параметрів
 Н/см2 ;
Н/см2 ;  Н/см2 ;
Н/см2 ;  Н/см2 ;
Н/см2 ; 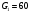 кг/год
кг/год 
Ємкості ресивера мають об’єм 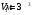 ;
; 
На основі матеріальних балансів складаємо рівняння статики для кожної із єкостей

Витрати  та
та  потрібно виразити через залежності від відповідних значень тиску, та ступеню відкриття клапану на вхідному потоці:
потрібно виразити через залежності від відповідних значень тиску, та ступеню відкриття клапану на вхідному потоці:
 ,
,
де  та
та  - коефіцієнти витрати;
- коефіцієнти витрати;  та
та  - це значення щільності газу відповідно перед вхідним клапоном та у першій ємкості.
- це значення щільності газу відповідно перед вхідним клапоном та у першій ємкості.

Враховуючи акумулюючу здатність кожної з ємкостей, перетворимо рівняння статики на рівняння динаміки:

За умовою, що
 та
та  ,
,
Отримуємл наступну систему диференційних рівнянь:

Зробимо аналіз змінних, що входять у рівняння. Змінними є :  . Якщо
. Якщо  та
та  будуть змінюватися, то навіть за сталим значенням
будуть змінюватися, то навіть за сталим значенням 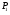 будуть змінюватися
будуть змінюватися  та
та  , а в зв’язку з тим, що
, а в зв’язку з тим, що  - змінна, то змінною буду і
- змінна, то змінною буду і  . Таким чином, змінними в рівняннях будуть
. Таким чином, змінними в рівняннях будуть  . Рівняння, з врахуванням визначенних змінних, будуть нелінійними. Лінеаризуємо рівняння розкладанням в ряд Тейлора.
. Рівняння, з врахуванням визначенних змінних, будуть нелінійними. Лінеаризуємо рівняння розкладанням в ряд Тейлора.

В рівняннях є залежні між собою змінні. Це тиск  та щільність
та щільність  , тиск
, тиск  та щільність
та щільність  . Іх однозначана залежність буде визначатися законом розширення газу. Якщо теплообмін з навколішнім середовищем близький до ідеального та не дуже великий перепад тиску, можна прийняти ізотермічний закон розширення газу PV=RT. Тоді можна записати:
. Іх однозначана залежність буде визначатися законом розширення газу. Якщо теплообмін з навколішнім середовищем близький до ідеального та не дуже великий перепад тиску, можна прийняти ізотермічний закон розширення газу PV=RT. Тоді можна записати:
 ,
, 
Введемо умовне позначення  .
.

Де 


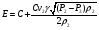
Виключивши з рівнянь змінни  та розділивши всі складові рівняння на коефіцієнт при
та розділивши всі складові рівняння на коефіцієнт при  , отримаємо:
, отримаємо:

Де 

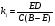


 ;
;  ;
;  ;
;
 ;
;  ;
;  ;
;
Розмірність всіх додатків рівняння динамікт однакова, що є необхідною, хоч і не достатьньою умовою стверджувати, що рівняння динаміки отримано вірно.
Визначимо із статичних залежностей та з довідників значення величин  . Спочатку визначимо
. Спочатку визначимо  . Тиск та щільність для незмінної температури знаходяться у такій залежності:
. Тиск та щільність для незмінної температури знаходяться у такій залежності:
 ,
,
де  - атмосферний тиск,
- атмосферний тиск,  Н/см2;
Н/см2;
 - абсолютне значення тиску відповідно перед ресивером, у першій та другій ємкості,
- абсолютне значення тиску відповідно перед ресивером, у першій та другій ємкості,  ;
;  ;
;  .
.
Щільність повітря ддля атмосферного тиску за довідником  кг/м3.
кг/м3.
Враховуючи викладне вище, із залежності вирахуємо числові значення  для основного статичного режиму:
для основного статичного режиму:
 ,
,  ,
, 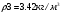
Визначимо числові значення коефіцієнтів витрати 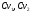 .
.



 .
.
Знайдемо числове значення виразу  ,
, 
 .
.
Запишимо значення всіх констант та змінних в номінальному (початковому) режимі в табл.2. Користуючись значенням величин, записаних у табл. 2, знайдемо числові значення проміжних коефіцієнтів B, D, C та E.
 ;
;  ;
;  ;
;  .
.
Таблиця 2
Значення параметрів ресивера в номінальноу статичному режимі
№ п.п
Назва параметру
Позначення
Розмірність
Числові значення
1.
Тиск повітря на вході
Н/см2
80
2.
Тиск повітря в першій ємкості
Н/см2
50
3.
Тиск повітря в другій ємкості
Н/см2
16
4.
Витрати повітря ()
Кг/год
60
5.
Об'єм першої ємкості
м3
3
6.
Об'єм другої ємкості
м3
5
7.
Ступінь відкриття клапану
-
0.5
8.
Щільність повітря на вході
Кг/м3
11.9
9.
Щільність повітря в перщій ємкості
Кг/м3
7.9
10.
Щільність повітря в другій ємкості.
Кг/м3
3.42
11.
Коефіцієнт витрати через клапан

6.35
12.
Коефіцієнт витрати парубка між ємкостями

3.6
13.

0.133
Користуючись розрахованими значеннями В, D, C та Е, а також значеннями параметрів із таблиці 1, з використанням залежностей обчислимо значення коефіціентів рівняння динаміки.
 год2 ;
год2 ;  год;
год; 
 ;
; 
 ;
; 
 .
.
Підставляючи значення коефіцієнтів у рівняння динаміки запишемо його у числовій формі
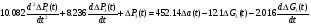 .
.
Це рівняння є рівнянням динамікт ресивера відповідно до залежності  .
.
Знайдемо розв'язання рівняння
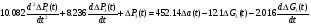
у вигляді  , де
, де  - вільна складова;
- вільна складова;  - примусова складова.
- примусова складова.
Початкові умови приймемо нульовими: 
Керуючий вплив визначаємо наступним чином:  . Збурюючий вплив
. Збурюючий вплив  та його похідну приймаємо нульовими. Харакеристичне рівняння диференційного рівняння має вид:
та його похідну приймаємо нульовими. Харакеристичне рівняння диференційного рівняння має вид:  ,
,  ;
;  .
.
Таким чином вільна складова вирішення має наступний вид:
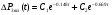
де, С1 та С2 – сталі інтегрування.
Примусова складова, у урахуванням того, що  не залежить від часу, складе:
не залежить від часу, складе:
 Н/см2
Н/см2
Для визначення сталих інтегрування С1 та С2 складемо систему равняння з урахуванням початкових умов та того, що похідна від  має наступний вид:
має наступний вид:

Система рівнянь формується наступним чином:


Звідси маємо:

Розв'язання системи рівняння дозволяє отримати такі значення С1 та С2:
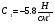 ,
,  .
.
Таким чином, остаточно запишемо розв'язання рівняння

За цією формулою проведемо розрахунки  , результати яких наведені в таблиці.
, результати яких наведені в таблиці.
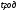

0
0
1
0,174
2
0,542
3
0,972
4
1,399
5
1,798
6
2,157
7
2,474
8
2,751
9
2,992
10
3,201

Нравится материал? Поддержи автора!
Ещё документы из категории физика:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ