Конспект урока на тему "Вписанная сфера"

 Вписанная сфера.
Вписанная сфера.
Определение: Сфера называется вписанной в многогранник, если она касается всех граней многогранника. Многогранник в таком случае называется описанным около сферы.
Центр вписанной сферы – точка пересечения биссекторных плоскостей всех двугранных углов.
Сфера называется вписанной в двугранный угол, если она касается его граней. Центр вписанной в двугранный угол сферы лежит на биссекторной плоскости этого двугранного угла. Сфера называется вписанной в многогранный угол, если она касается всех граней многогранного угла.
Не во всякий многогранник можно вписать сферу. Например: в прямоугольный параллелепипед, не являющийся кубом, сферу вписать нельзя.
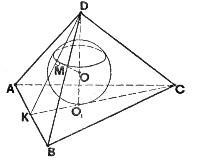
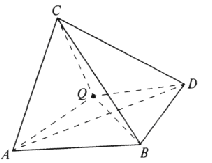
Теорема. В любую треугольную пирамиду можно вписать сферу и притом только одну.
Доказательство. Рассмотрим треугольную пирамиду CABD. Проведем биссекторные плоскости ее двугранных углов с ребрами AС и BC. Они пересекаются по прямой, которая пересечет биссекторную плоскость двугранного угла с ребром АВ. Таким образом, биссекторные плоскости двугранных углав с ребрами АВ,АС и ВС имеют единственную общую точку. Обозначим ее Q. Точка Q равноудалена от всех граней пирамиды. Следовательно, сфера соответствующего радиуса с центром в точке Q является вписанной в пирамиду САBD.
Докажем ее единственность. Центр любой сферы вписанной в пирамиду CABD равноудален от ее граней, значит, он принадлежит биссекторным плоскостям двугранных углов. Следовательно, центр сферы совпадает с точкой Q. Что требовалось доказать.
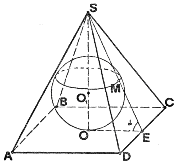
Теорема. В пирамиду, у которой в основание можно вписать окружность, центр которой служит основанием высоты пирамиды, можно вписать сферу.
Следствие. В любую правильную пирамиду можно вписать сферу.
Докажите, что центр сферы вписанной в правильную пирамиду, лежит на высоте этой пирамиды (докажите самостоятельно).
Центр сферы, вписанной в правильную пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.
Проанализируйте решение задачи.
Задача. В правильной четырехугольной пирамиде сторона основания равна а, высота равна h. Найдите радиус сферы, вписанной в пирамиду.
Решите задачу.
Задача. В правильной треугольной пирамиде сторона основания равна 4, боковые грани наклонены к основанию под углом 600. Найдите радиус, вписанной в эту пирамиду сферы.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ