Конспект урока по геометрии "Четырехугольники" 8 класс
Открытый урок по геометрии в 8-м классе по теме: "Четырехугольники"
![]()
Цели урока:
повторение понятия четырехугольника, его видов, свойств, практические способы определения видов четырехугольников;
развитие математической речи, умения систематизировать и обобщать знания;
воспитание самостоятельности, активности.
Ход урока
Вступительное слово учителя.
Мы закончили изучать тему “Четырехугольники”. Цель урока – повторить определения четырехугольника, параллелограмма, их видов; обобщить свойства этих фигур, показать применение этих свойств на практике. Все эти знания помогут нам при изучении свойств тел в дальнейшем при решении задач стереометрии.
Запишите в тетрадях число, тему урока.
Итак,
І этап работы:
Повторим определения и свойства четырехугольников
Фронтальный опрос /устно/.
1 - что называется четырехугольником? /Cоставляем диаграмму, изображающую четырехугольни-ки и его виды в виде разноцветных кругов, накалывая их на доску/;
2 – назовите виды четырехугольников;
3 – что называется параллелограммом?
4 – назовите свойства параллелограмма;
5 – что называется прямоугольником?
6 – назовите свойства прямоугольника;
7 – что называется ромбом?
8 – назовите свойства ромба;
9 – что называется квадратом?
10- назовите свойства квадрата;
11- что такое трапеция?
12- назовите виды и свойства трапеции.
/ В процессе опроса на доске появляется диаграмма./
В процессе опроса на доске появляется диаграмма./
II этап. Историческая справка.
Сейчас вы услышите рассказы, почему четырёхугольники так называются (учащиеся представляют заранее подготовленные сообщения)
1 ученик: Термин «параллелограмм» греческого происхождения и согласно Проклу, был введён Евклидом.
Понятие параллелограмма и некоторые его свойства были известны ещё пифагорейцам. В «Началах» Евклида доказывается следующая теорема:
в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная теория параллелограмма была разработана к концу средних веков и появилась в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.
Параллелограмм даёт определения прямоугольнику, ромбу; в жизни параллелограмм – это рамы велосипедов, мотоциклов, где для жёсткости проведена диагональ. В физике параллелограмм применяется при изучении разложения сил, при нахождении равнодействующих сил.
2 ученик: Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Ромб связывали первоначально с сечением, проведённым в обмотанном веретене. В «Началах» Евклида термин «ромб» встречается только один раз, свойства ромба вообще не изучаются.
Реечный домкрат для легковых автомобилей имеет форму ромба. Плиточники укладывают плитку в виде ромба, квадрата – из них получаются красивые узоры.
3 ученик: Термин «квадрат»происходит от латинского слова – сделать четырёхугольным.
«Первый четырёхугольник, с которым познакомилась геометрия, был квадрат»
Трапеция – слово греческое, означавшее в древности «столик». Сравните трапеза, трапезная. В «Началах» термин «трапеция» применяется не в современном, а в другом смысле: любой четырёхугольник (не параллелограмм). «Трапеция» в нашем смысле встречается впервые у древнегреческого математика Посидония.
III этап работы.
Мы повторили определения и свойства четырехугольников, проверим теперь, как вы видите эти свойства в фигурах.
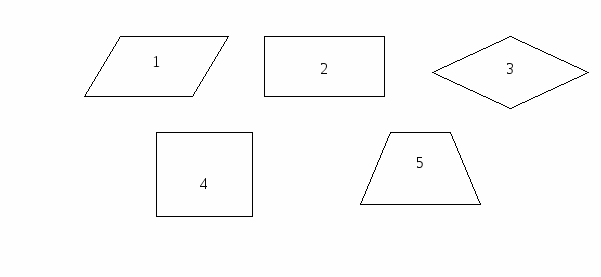
Математический диктант. (На доске заранее нарисованы фигуры).
Отвечая на вопросы диктанта, пишем ответ – номер фигуры, обладающей данным свойством.
У какой из фигур диагонали, пересекаясь, делятся пополам?
У какой из фигур диагонали равны?
У какой из фигур диагонали делят углы пополам?
У какой из фигур диагонали перпендикулярны?
У какой из фигур диагонали равны и перпендикулярны?
У какой из фигур равны противолежащие углы?
У какой из фигур равны все углы?
У какой из фигур равны углы, прилежащие к одной стороне?
У какой из фигур противолежащие стороны попарно параллельны?
У какой из фигур параллельна пара противолежащих сторон?
Взаимопроверка. Поменяйтесь тетрадями и карандашом или цветной пастой проверьте диктант товарища.
Ответы заготовлены заранее на доске и закрыты.
IV этап работы.
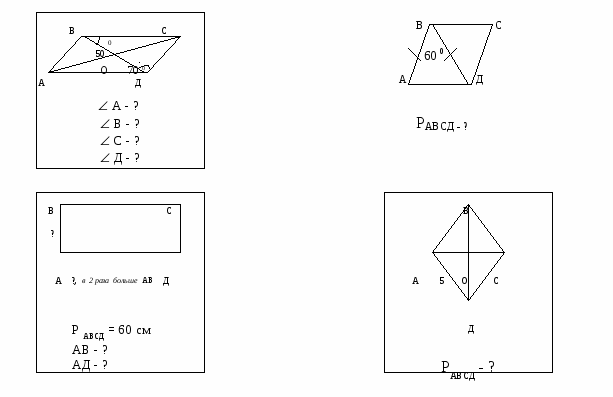
Устно решаем задачи, предложенные на плакатах.
Vэтап. Вывод. Подведение итогов.
Итак, мы повторили определения и свойства четырехугольников, говорили об их практическом применении, о нахождении различных элементов четырехугольников.
Оценки за диктант и практическую работу будут выставлены к следующему уроку.
VI этап. Домашнее задание.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ