Метрические соотношения в треугольнике и окружности
Тема: Метрические соотношения в треугольнике и окружности. 2чт.
Цель: Организовать деятельность учащихся по обобщению и систематизации знаний по теме.
Ход урока.
Тема и цель урока, слайд 1.
Основные факты и теоремы по этой теме, слайд 2.
Метрические соотношения в прямоугольном треугольнике.
Теорема Пифагора
Тригонометрические функции.
Теорема косинусов.
Теорема синусов.
Свойство хорд.
Свойство секущих.
Какие соотношения справедливы в прямоугольном треугольнике, слайд 3
В прямоугольном треугольнике справедливы следующие соотношения:
h2 = a1 *b1;
b2 = b1 * c;
a2 = a1 * c, где b1 и а1 – проекции катетов b и а на гипотенузу.
С
П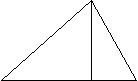 ример: а1 = 3, b1 = 6,
ример: а1 = 3, b1 = 6,
а =? b =? h =? с =? а b
Решение: с = 9, а2 = 27, h
b2 = 54, h = 18 В А
а1 b1
Сформулируйте теорему Пифагора, слайд 4
Квадрат гипотенузы в прямоугольном тр-ке равен сумме квадратов катетов:
с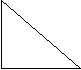 2 = а2 + b2
2 = а2 + b2
Пример: а = 12, b = 5, с =?
а с Решение: с2 = 169, с = 13
b
Определение тригонометрических функций, слайд 5
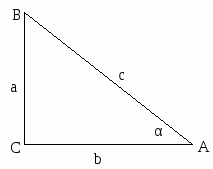
Синусом угла a называется отношение противолежащего катета к гипотенузе: sin a = ВС/АВ
Косинусом угла a называется отношение прилежащего катета к гипотенузе: cos a = АС/АВ
Тангенсом угла a называется отношение противолежащего катета к прилежащему: tg a = АВ/АС
Котангенсом угла a называется отношение прилежащего катета к противолежащему: ctg a = АС/ВС
Пример: а = 5, b = 12, c = 13.
Найти: sin A, cos A, tg A, ctg A
Решение: sin A = 5/13, cos A = 12/13, tg A = 5/12, ctg A = 12/5.
Вспомните формулировку теоремы косинусов, слайд 6
В произвольном треугольнике справедливо равенство: а2 = b2 + c2 ± 2bc cosa
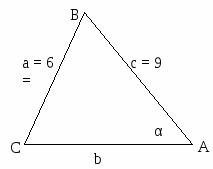
Пример: 1) b = 2, c = 5,a = 600, а =?
2) а = 6, b = 8, с = 9, cos a =?
Решение: 1) а2 = 4 + 25 - 20*1/2 =19
2) cos a = (64 + 81-36): 2*8*9=0,75
Вспомните формулировку теоремы синусов, слайд 7
В произвольном треугольнике справедливо равенство: ![]() , где R – радиус описанной окружности.
, где R – радиус описанной окружности.
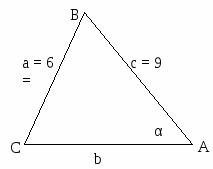
Пример: а = 4, sin A = ½, b = 6, sin B =?
Решение: 8 = 6 / sin B, sin B = ¾
Сформулируйте свойство хорд, слайд 8
Произведение ВА*АВ1 = R2 – a2 постоянно.
 В
В
 С Пример: ВА = 2, АВ1= 6, СА = 4, СА1 =?
С Пример: ВА = 2, АВ1= 6, СА = 4, СА1 =?
Решение: СА1 = 12:4 = 3
С1 В1
Сформулируйте свойство секущих, слайд 9
АВ*АВ1 = АС*АС1 = а2– R2

 А Пример: АВ = 3, АВ1 = 8, АС = 6, АС1 =?
А Пример: АВ = 3, АВ1 = 8, АС = 6, АС1 =?
 Решение: АС1 = 3*8 / 6 = 4
Решение: АС1 = 3*8 / 6 = 4
 В
В
 С
С
В1
С1
Решение задач:
работают в парах, затем сравнивают свое решение с решением на слайде.
1. В равнобедренном треугольнике боковая сторона равна 17, а высота, опущенная на основание, равна 15. Найти основание треугольника.
 А Решение: ВК = 8, ВС = 16
А Решение: ВК = 8, ВС = 16
17 Ответ: ВС = 16
15
В К С
2. Две стороны треугольника равны 3 и 7, а угол, противолежащий большей из них, равен 600. Найдите третью сторону треугольника.

3 7
600
 х
х
Решение:
49 = х2 + 9 – 2*3*х*1/2
х2 – 3х – 40 = 0, х = 8, -5.
Ответ: 8
3. Один из углов треугольника равен 300, а диаметр окружности, описанной около треугольника, равен 14. Найдите сторону, противолежащую данному углу.
Решение:
2R = 14, а/sin300 = 14, а = 7
а Ответ: 7
 300
300
4. Решите треугольник АВС, если угол А = 450, угол В = 750, АВ = 2Ö3.

 С
С
 А 450 750 В
А 450 750 В
Решение:
ВС : sin450 = 2Ö3 : sin600, BC = 2Ö3 sin450 : sin600, BC = 3Ö2
AC : sin750 = 2Ö3 sin600 , AC = 2Ö3 sin750 : sin600
3. Итоги урока.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ