Государственное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа№44

Приморского района Санкт-Петербурга

Конспект урока по геометрии
в 10 классе

«Тайна египетского треугольника»

подготовила

учитель математики

Сироткина Елена Анатольевна

г. Санкт-Петербург

2012

Конспект урока по геометрии

для 10 класса

«Тайна египетского треугольника»

Тип урока: урок-семинар.

Цель:

Показать взаимосвязь наук на примере изучения египетского треугольника (золотого сечения).

Задачи:

1. Расширить знания учащихся о прямоугольном треугольнике со сторонами 2,4, 5;

2. Показать связь между знаниями людей в различных областях наук: геометрии, химии, истории.

3. Воспитывать у учащихся любознательность, пытливость, стремление расширять свой кругозор.

При подготовке урока использованы материалы сайтов:

• http://www.shaping.ru/mku/babanin04.asp

• http://www.goldenmuseum.com/0302pyramids_rus.html

• http://tainy.net/8969-tajna-geometrii-piramid-v-egipetskom-treugolnike-i-v-zolotom-sechenii.html:

План урока:

1. Священные числа 3, 4, 5, 12

2. Древнеегипетский стандарт - прямоугольный треугольник

3. Священные две трети пирамиды и золотое сечение

4. Тайны египетского треугольника в молекуле воды

5. Заключение. Итоги.

Ход урока:

1.Оргмомент.

2.Сообщение темы урока.

Презентация

Сегодня у нас необычный урок. Мы заново будем знакомиться с египетским треугольником.

Но сначала небольшая разминка. Запишите 2 члена ряда

1) 8,01; 8,002; 8,0003...

2) 2,5,11,25,47...

3) 1/2; 2/9; 4/16; 8/23...

3. Священные числа 2, 4, 5, 12.

Презентация

Знали ли в древнем Египте математику и геометрию? Не только знали, но и применяли при создании архитектурных шедевров, при ежегодной разметке полей. Существовала специальная служба землемеров, которые с помощью геометрических приемов восстанавливали границы полей, когда вода спадала.

Для нас самым простым математическим действием является 2*2 = 4. Для египтян самой простой считалась теорема о треугольнике со сторонами 3, 4, 5.

У вас было творческое домашнее задание - узнать как можно больше информации об египетском треугольнике. ( Отмечаем. Среди ответов учащихся: 3 + 4 + 5 = 12 — это также священное число.)

4. Древнеегипетский стандарт - прямоугольный треугольник.

Прямоугольный треугольник с соотношением сторон 3:4:5 был своеобразным стандартом древнего Египта.

Презентация

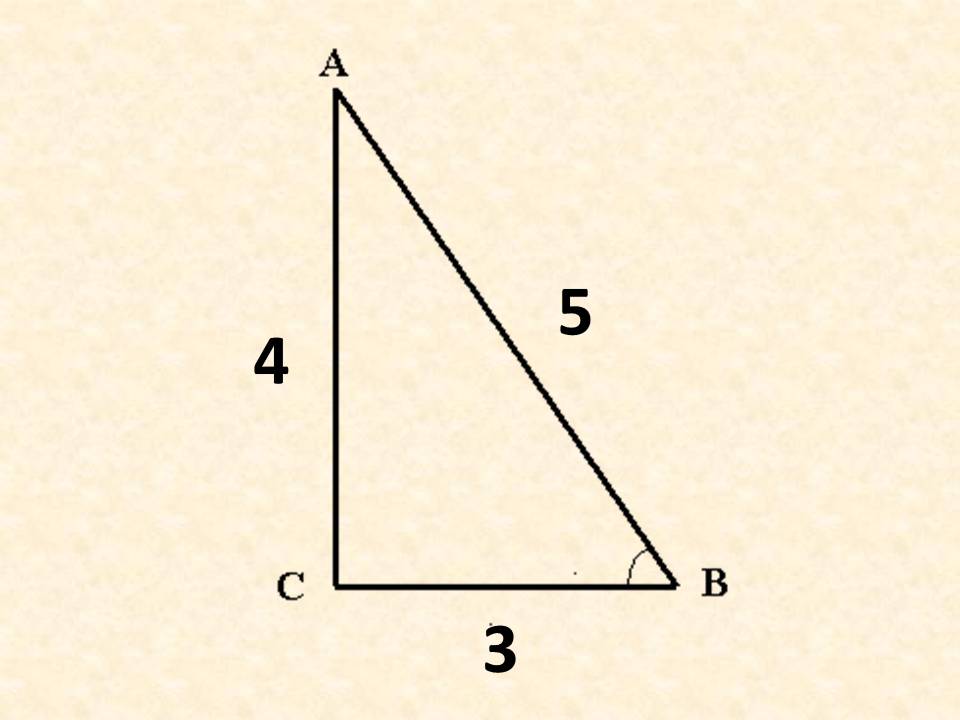
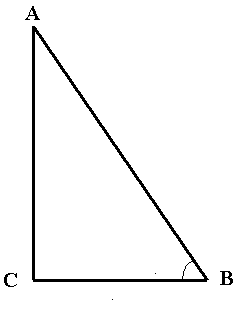
При этом чему равен угол АВС?

Ответ учащихся: угол АВС = 51^е 50 (из д/задания)

Эта величина нам скоро пригодится.

А пока вопрос? Как египтяне вычисляли стороны треугольника, ведь возводить в квадрат и извлекать корни они еще не умели.

Единицами измерения тогда были не см, м и т.д., а локоть, ладонь и палец. Для составления плана строительных работ существовала еще единица - секед 5 ¼ ладони, т.е. 5 ладоней и 1 палец, тогда можно вычислить длины сторон треугольника.

Решаем задачу:

Задача:

Дано: Решение:
АС = 5 ¼ ладони (секед) ВС/АС = 4/3 - ВС = 5 ¼ 4/3 = 7 ладоней
Найти: АВ/АС = 5/3 = АВ = 5 ¼ 5/3 = 8 ¾ ладони
ВС и АВ (т.е. 8 ладоней и 3 пальца)

Так египтяне без возведения чисел в квадрат и извлечения корней решали математические задачи. Хотя надо оговорить, что им заранее было известно соотношение сторон в прямоугольном треугольнике 3:4:5.

Но почему именно такой треугольник стал для египтян основным элементом математических вычислений? Идём дальше.

5.Священные две трети пирамиды.

Этот эталон отношений сторон в прямоугольном треугольнике знали даже в школах Древнего Египта, о чем свидетельствует « Папирус Ахмеса». В нем приведены задачи на вычисление размеров и объем пирамид. Рассмотрим одну из таких задач.

Задача:

По длине основания 140 локтей, а также середу – 5 ¼ ладони требовалось найти высоту.

Презентация

В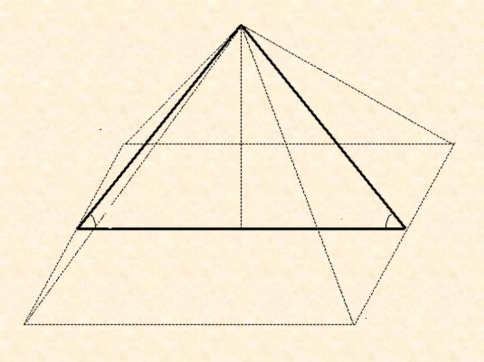 результате приведенных, несколько замысловатых рассуждений h = 93 1/3 локтя.

Теперь проверим: 140* 2/3 = 93 1/3

Почему 2/3? Да потому, что это вытекает из геометрии египетского треугольника.

Построим сечение идеальной, выполненной с соблюдением всех требований египетского стандарта, пирамиды. Это сечение - треугольник SМN - образован сложением двух египетских треугольников, где SО - катет, с соотношением 4, является общим. А теперь найдем отношение

SО : МN, оно = 2/3 . С чем связана эта величина?

Ответ учащихся: с золотым сечением.

Значит, в идеальном случае, прямоугольный треугольник с соотношением сторон 3:4: 5 и острым углом 53 08 еще и обладал гармоничными пропорциями золотого сечения!!!

Не здесь ли заключена его тайна? Не будем торопиться с выводами.

Обратимся к некоторым кадрам...

Презентация

Вот так выглядят реальные пирамиды. Рассмотрим их параметры

У пирамиды Хеопса сторона основания 233 м, а высоту рассчитаем сами: h = 233 *2/3 = 155,3 м.

Фактически h = 146 м и угол наклона боковой грани 51 52.

У пирамиды Хефрена а = 215 м, => h = 215 * 2/3 =143,3 м.

Фактически h = 143 м и угол наклона 53 12 - почти равен 53 08

А как же пирамида Менкаура? Смог ли он повторить успех своих родных?

Менкаур был более мягким властителем, чем его отец Хафрен и дед Хеопс. При нем народ почувствовал себя свободней. Но при этом, вероятно, снизилась требовательность в строительстве.

При стороне основания а = 108 м, высота h должна быть

h =108 * 2/3 = 72 м. Фактически h = 66 м и угол наклона 51 .

Т.о. пирамида Хефрена более близка к идеальной - в сечении двойной египетский треугольник и высота пирамиды находится с основанием в золотой пропорции.

6.Тайна геометрии пирамид в египетском треугольнике и в золотом сечении.

Итак, египетский треугольник 3:4:5. Кто же придумал этот геометрический шедевр -человек или природа? Какие еще соотношения в треугольнике можно обнаружить?

Ответ учащихся: Например, такое 3 + 5= 8.

Стоп! А где еще выстроились такие числа, да еще в ряд? Смотрим, в начале урока у нас был такой ряд: 1, 1, 2, 3, 5, 8, 13... Это золотой ряд! Древние египтяне знали, с чем имели дело!

Вспомним, как разделить отрезок в золотом отношении.

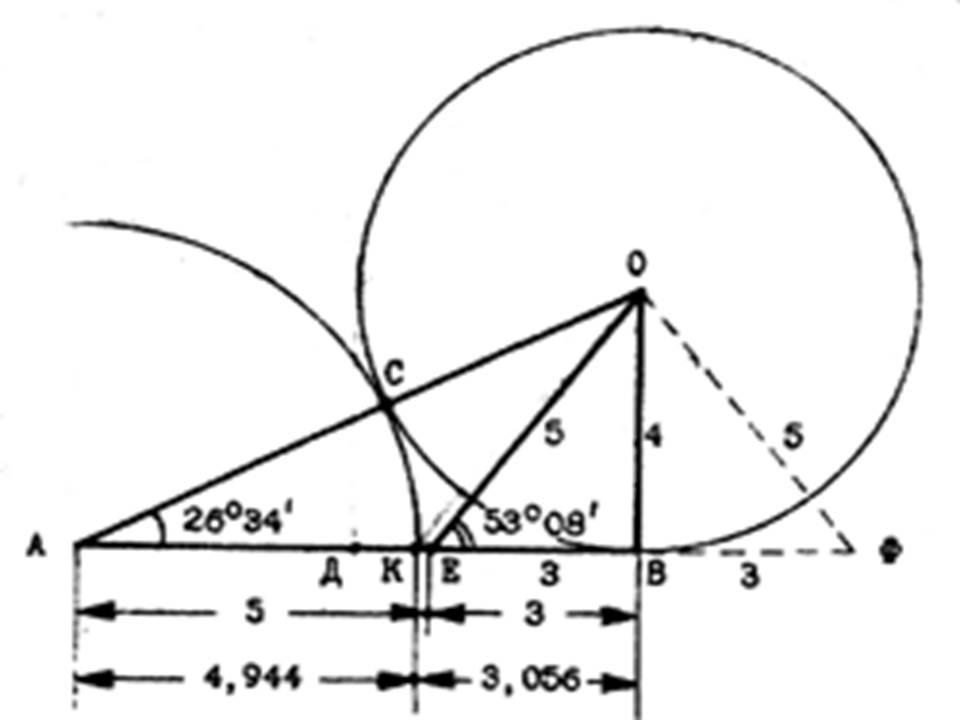
Задача:

Разделить отрезок АВ в золотом отношении

Один ученик решает на доске, остальные в тетради.

Но у задачи есть продолжение.

Где-то здесь спрятан египетский треугольник.

Попробуем его найти!

Если соединить Е и О, то это и будет египетский треугольник. Ну кто бы мог подумать , что он спрячется в таком месте?

Поистине - он дитя золотого сечения. Но пока мы не ответили на вопрос - почему этот треугольник создан природой. Обратимся к другой науке- химии. Выступление ученицы 10 ^«А" класса.

7."Тайна египетского треугольника в молекуле воды!"

В химии формула молекулы воды Н2О также популярна, как в математике 2*2 = 4.

Молекула состоит из 1 атома кислорода и 2 атомов водорода. Для нас очень важно, как располагаются относительно друг друга ядра атомов водорода и кислорода.

В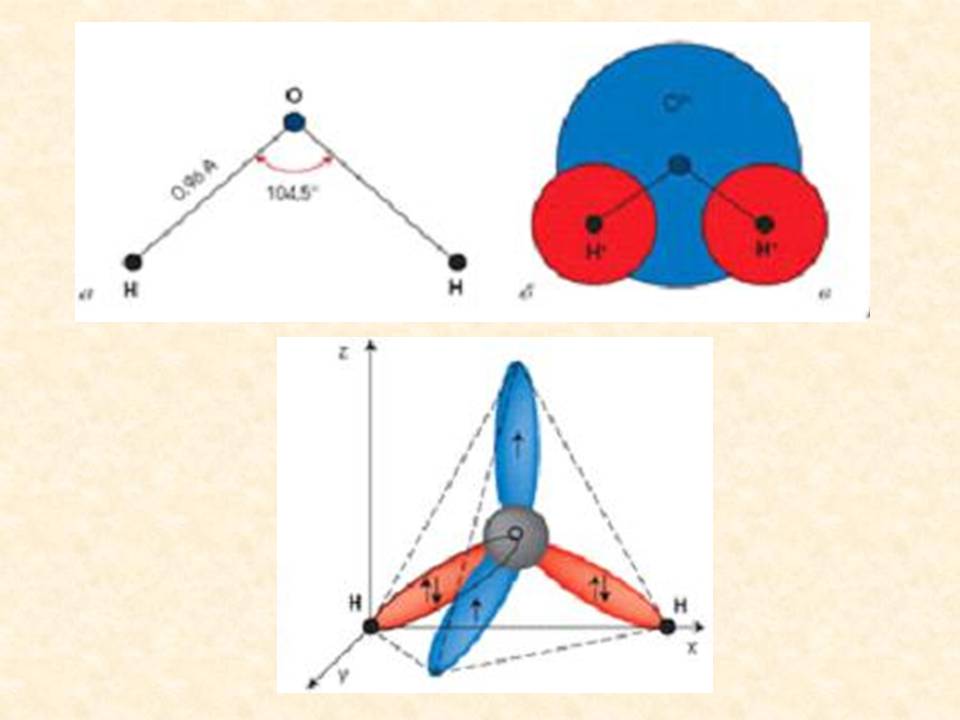 молекуле воды они образуют равнобедренный треугольник, длина сторон которого и угла между ними изменяется в некоторых пределах при изменении окружающих условий.

Например, если молекула воды находится в парообразном состоянии в равновесии, то длина боковой стороны = 0,96 ангтрем, а угол между ними =104 26 . Лёд является одним из состояний воды. Для молекул льда боковые стороны равнобедренного треугольника = 0,99 ангстрем, а угол между ними 109,4.

Где-то здесь спрятан египетский треугольник! Разделим эти углы пополам:

104 26 : 2 = 53 13

109,5 6 : – 54,32

А в египетском треугольнике угол = 53 08 ' . Но он так близок! Не почувствовать, не ощутить его невозможно.

Здесь, где-то вблизи перехода в ледяной кристалл, когда структура воды приближается к закономерному строению кристаллического тела, находится египетский треугольник.

8. Заключение. Итоги.

Становится понятным, что знаменитый египетский треугольник "взят" из молекулы воды, которая образована двумя египетскими треугольниками, имеющими общий катет с соотношением стороны = 3.

Истинным создателем молекулы воды, а значит и египетский треугольник, является сама природа.

Именно поэтому в нем заложена та гармония, которая присуща всему космосу, и которая выражается, в частности свойствами золотого сечения.

Только этим можно объяснить, почему египтяне обожествляли числа 3, 4, 5, а сам треугольник считали священным и буквально нянчились с ним, как с младенцем, стараясь заложить в любую конструкцию, в пирамиды, даже в разметку полей.

Великие пирамиды своей кристаллоподобной формой отражают структуру и скрытые свойства воды - самого важного для всего живого.

И все другие пирамиды, содержащие египетский треугольник, а с ним и золотое сечение, которые существовали или существуют на всех континентах Земли и на других планетах, в том числе на Марсе, были созданы по тому же принципу, что и великие пирамиды Египта.

Они открывают нам ворота в другие миры, которые пока остаются для нас непознанными.

Список использованной литературы

1. "Тайны великих пирамид" В.Бабанин

2. "Жезлы горя" В.М.Уваров

3. "История математики в школе" Г.И.Глейзер -

4. Математика Большой энциклопедический словарь

5. "Секреты пирамид" Р.Бьювел, Э.Джильберт

6. "За страницами учебника математики" И.Я.Депман, Н.Я.Виленкин

7. "За страницами учебника алгебры" А.Ф.Течурин

Интернет-ресурсы

• http://www.shaping.ru/mku/babanin04.asp

• http://www.goldenmuseum.com/0302pyramids_rus.html

• http://tainy.net/8969-tajna-geometrii-piramid-v-egipetskom-treugolnike-i-v-zolotom-sechenii.html: