Урок геометрии для 7 класса «Искусство рассуждать»
Урок геометрии в 7 классе
Тема урока: «Искусство рассуждать»
Учитель: Юрова Галина Евгеньевна,
МБОУ СОШ № 8 г. Каменск-Шахтинский
Урок построен на основе технологии проблемно-исследовательского обучения.
Целевое назначение.
1. Активизация и развитие качеств продуктивного мышления.
2. Развитие творческих способностей.
3. Формирование методов и способов научного познания, исследовательских навыков, поисковых процедур.
4. Стимулирование познавательных мотивов: интереса, стремления проникнуть в сущность явлений, осознание значимости знаний.
5. Развитие способностей к анализу, рефлексии.
Последовательность этапов.
1. Создание проблемной ситуации.
· Организация и актуализация определенного опыта, предшествующего проблемной ситуации.
· Организация сбора фактов о каком-либо объекте или явлении.
· Предъявление интересного детям задания (исследовательского проекта), для решения которого у учащихся нет знаний или опыта.
· Создание условий для эмоционального переживания, удивления перед парадоксальностью факта, стимулирование потребности объяснить, разрешить противоречие.
2. Формулирование проблемы.
· Самостоятельный анализ ситуации, выявление противоречивых моментов, отделение известного от неизвестного.
· Самостоятельное формулирование проблемы.
· Планирование этапов и способов решения проблемы.
3. Выдвижение гипотез.
· Самостоятельный (и групповой) сбор фактов, дающий основание для выдвижения гипотез .
· Самостоятельное выдвижение гипотез индивидуально и в групповом обсуждении методом “мозговой атаки” (стимулирование догадки, интуиции).
4. Поиск решения проблемы.
Самостоятельная (и групповая) проверка каждой из гипотез путем: а) дополнительного сбора фактов; б) подведения под известные теоретические знания; в) анализа и дедуктивного обоснования; г) экспериментальной проверки и наблюдения .
5. Формулирование выводов.
· Оформление выводов в виде письменного логического обоснования;
· Формулирование обобщенных выводов, условий, систематизация знаний по проблеме.
6. Применение выводов на практике.
· Самостоятельное составление заданий на применение нового знания.
· Иллюстрация верности найденного способа решения проблемы на задачах данного класса.
Цели урока
Образовательные: ознакомление учащихся с методом доказательства от противного, с математическими софизмами.
Развивающие: развитие способности логически мыслить, выделять проблему и искать пути ее решения, приобщение к научному поиску, развитие умения отстаивать свое мнение.
Воспитательные: привитие интереса к математике, развитие навыков работы в группе, критического отношения к мнению другого.
Оборудование: компьютер, проектор, раздаточный материал, разноцветные(разноуровневые) карточки с заданиями.
«Величие человека в его способности мыслить»
Б.Паскаль
Оргмомент.
Приветствие.
Оцените свое настроение в начале урока, закрасив ту рожицу, которая ему соответствует.
 Большую часть информации мы получаем с помощью глаз, зрения. Но не могут ли наши глаза обманывать нас? Я предлагаю вам рассмотреть несколько рисунков. Слайды:
Большую часть информации мы получаем с помощью глаз, зрения. Но не могут ли наши глаза обманывать нас? Я предлагаю вам рассмотреть несколько рисунков. Слайды:






Сравните на глаз длины отрезков АВ и ВС на первых двух рисунках, и определите на глаз прямые или кривые длины на рисунках 3-6.
А теперь воспользуйтесь линейкой и ответьте на эти вопросы еще раз.
Вывод делают дети: зрения человека дает не точную, а иногда ошибочную информацию. Что же делать? Измерять?
Вывод делают дети: самые тщательные измерения оставляют повод для сомнения, так как в них неизбежны ошибки. Кроме того, под рукой может не оказаться измерительных инструментов, да и для всех фигур данного вида невозможно проделать измерения.
Вывод делают дети: надо учиться рассуждать.
Итак, тема урока: «Искусство рассуждать».
Есть такая наука, которая учит, как нужно рассуждать, чтобы наше мышление было определенным связным, последовательным, доказательным и непротиворечивым. Кто знает, что это за наука? (Логика). Я не сомневаюсь, что голова у вас ломится от мыслей, но эти мысли надо упорядочить, направить в русло полезной работы.
Математика поможет вам справиться с этой задачей. Недаром говорят, что математика это гимнастика для ума.
В Древней Греции всех ораторов учили геометрии. На дверях школы было написано: «Незнающий геометрии да не войдет сюда». Это объясняется тем, что геометрия учит рассуждать и доказывать. Речь человека убедительна, когда он доказывает свои выводы.
Считается, что первыми стали применять доказательство древние грехи (6 век до н.э.) Фалес из Милета первым начал игру в «Докажи», которая и продолжается уже 2,5 тысячелетия и конца которой не видно.
Доказательство любой темы это цепочка логических умозаключений, сводящих доказываемую теорему к ранее доказанным теоремам, аксиомам и определениям.
Фронтальная работа:
А знаете ли вы, что такое определение? Аксиома? теорема? (опрос детей).
Всякая теорема имеет условие и заключение. Слайды:


Для любой теоремы можно сформулировать обратную, если условие и заключение поменять местами. Слайд:

Но обратная теорема не всегда верна. Давайте попробуем исследовать, верны ли обратные теоремы для предложенных. Слайд:

Итак, утверждение, обратное второму мы назвали верным.
Но истинность всегда приходится доказывать. Доказательство проводят опираясь на аксиомы, определения, уже доказанные свойства фигур. Например, доказательство равенства вертикальных углов перед вами. Слайд:

Исследуйте, каким определением и свойствами воспользовались при доказательстве этой теоремы.
Есть еще один способ доказательства: от противного. Латинское «приведение к абсурду». Слайд. На столе каждого ребенка алгоритм доказательства методом от противного.

Пример, Доказать, что паук – это не насекомое.
Исследовательская работа:
А теперь я предлагаю вам исследовательскую работу. Попробуйте самостоятельно доказать утверждение методом от противного. Я не сомневаюсь, что вы замечательно справитесь с заданием, но если вы не уверены в себе на все 100%, то я вам предлагаю выбрать себе задание по степени сложности синяя, зеленая, желтая, белая, красная. На выполнение задания дается строго регламентированное время 3 минуты.
Синяя: Докажите методом от противного, что если углы не равны, то они не вертикальные.
Зеленая: Докажите методом от противного, что два смежных угла не могут быть оба тупыми.
Желтая: Докажите методом от противного, что если в школе 500 Белая: Докажите методом от противного, что во всяком треугольнике против большего угла лежит большая сторона.
Красная: Докажите методом от противного, что если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Групповая работа:
Распределение по группам. Обсуждение. Выбор представителя. Заслушивание. Самооценка.
Занимательная математика:
Я хочу вас познакомить с одним математическим понятием – софизмом. Софизм – это заведомо ложное умозаключение, имеющее видимость правила. То есть в доказательстве намеренно допускается ошибка, которая приводит к абсурду.
Так, например, можно доказать, что 1=2.
Слайды:
Найдите ошибку в рассуждениях.
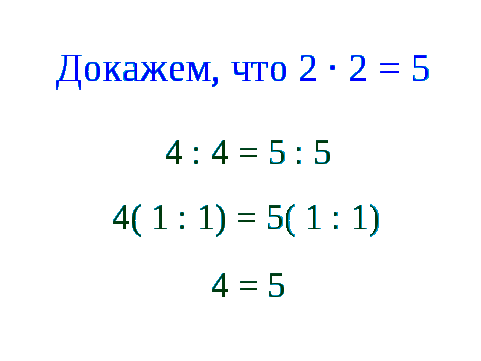

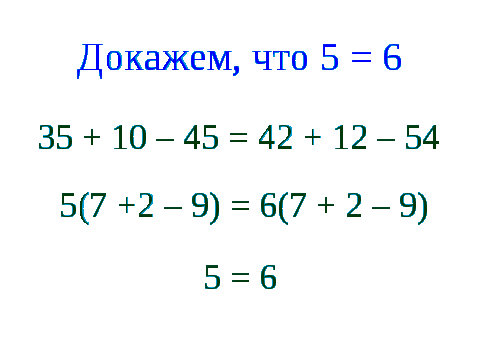
Подведение итогов уроков. Рефлексия. Оцените свое настроение в конце урока.

Нравится материал? Поддержи автора!
Ещё документы из категории геометрия:
Чтобы скачать документ, порекомендуйте, пожалуйста, его своим друзьям в любой соц. сети.
После чего кнопка «СКАЧАТЬ» станет доступной!
Кнопочки находятся чуть ниже. Спасибо!
Кнопки:
Скачать документ